Мониторинговые исследования в 8 классе как метод обеспечения преемственности в методике обучения математике

ОДЕЛ ОБРАЗОВАНИЯ АДМИНИСТРАЦИИ НОВОАЗОВСКОГО РАЙОНА

РАЙОННЫЙ МЕТОДИЧЕСКИЙ КАБИНЕТ ОТДЕЛА ОБРАЗОВАНИЯ

АДМИНИСТРАЦИИ НОВОАЗОВСКОГО РАЙОНА

МЕТОДИЧЕСКАЯ РАЗРАБОТКА

Учителя математики высшей квалификационной категории, учителя методиста Новоазовской общеобразовательной школы І-ІІІ ступеней №1

ХОРУЖЕНКО ЕЛЕНЫ ВАЛЕНТИНОВНЫ

Мониторинговые исследования в 8 классе как метод обеспечения преемственности в методике обучения математике и организации учебно-познавательной деятельности обучающихся.

Новоазовск 2019

Оглавление

Раздел 1. Обоснование актуальности темы разработки 3

Раздел 2. О мониторинге качества математического образования 4

Раздел 3. Проблема преемственности в педагогике и методике математики 7

Раздел 4. Реализация преемственности через систематизацию и обобщение знаний 9

Раздел 5. Опыт работы. 11

5.1. Ведущая педагогическая идея. 11

5.2. Технология опыта 12

5.3 Результативность 16

Выводы 18

Список литературы 19

Приложение. 22

Раздел 1. Обоснование актуальности темы разработки

На современном этапе развития школы определены приоритетные направления на компетентность, дифференциацию среднего образования с ориентацией процесса обучения на индивидуальные интересы личности. Переход школы к многообразию образовательных систем приводит к необходимости обеспечения преемственности в обучении математике, что особенно актуально в условиях новых Государственных стандартов и новых учебных программ по математике.

Методике преподавания математики во все периоды развития школы отводилось одно из ведущих мест. В связи с этим возникает необходимость обеспечения преемственности в методике обучения арифметике и алгебре и организации учебно-познавательной деятельности обучающихся на уроке.

В методическом пособии предлагается продолжить осмысление

проблемы мониторингового исследования как метода обеспечения преемственности в обучении.

Имея базовую теоретическую подготовку, на практике учитель встречается с необходимостью личностного осмысления проблемы преемственности в разных аспектах, на разном содержательном материале. Подчеркивая важность осуществления преемственности при переходе из начальной в основную и из основной в среднюю школу, а также из школы в высшие или средние специальные учебные заведения, предлагается с опорой на познанное рассмотреть наиболее трудный этап в процессе обучения: преемственную связь арифметики и алгебры при переходе от пропедевтического к систематическому курсу.

В приложения методической разработки включены варианты диагностической контрольной работы в 8 классе, разработанные с учетом выбранной темы.

Предлагаемая структура и содержание методического пособия позволяют показать связь между мониторинговыми исследованиями и преемственностью в обучении математике на примере процесса обобщения и систематизации знаний в практической деятельности учителя.

Материалы пособия могут быть использованы при совершенствовании содержания и методов обучения арифметике и алгебре в основной школе, при подготовке к диагностической контрольной работе в 8 классе для учителя и обучающихся. Методическое пособие может быть использовано для самостоятельного изучения проблемы учителями в процессе самообра-зования.

Раздел 2. О мониторинге качества математического образования

Важным направлением работы каждого педагога республики есть участие в создании республиканской модели мониторинга качества образования, включая мониторинг повышения уровня знаний обучающихся на основе самообразовательной деятельности и творческих способностей по математике.

Мониторинг – это важный инструмент переориентации деятельности школы от формальных показателей внутришкольного контроля к нуждам развития личности обучающихся. Мониторинг качества образования, который разрабатывается творческими работниками образования ДНР, обеспечит углубленный, объективный, многомерный анализ, позволит оценить процесс развития региональной системы образования и выявить ведущие тенденции, педагогические закономерности. Один из этапов образовательного мониторинга использование системы отслеживания учебных достижений обучающихся по базовым дисциплинам в соответствии с государственным планом контроля за обучающимся процессом в общеобразовательном учреждении, которое обеспечивает качественное образование. Предметный мониторинг в системе образовательного мониторинга позволяет следить за процессом согласно определенной программы, сопоставлять полученные результаты и сравнивать их с запланированными. Он охватывает основные задачи современной школы с акцентом на предоставление обучающимся знаний, прежде всего в объеме Государственного образовательного стандарта. Основным показателем системы знаний и умений обучающихся по учебному предмету является уровень учебных достижений.

Отслеживание учебных достижений обучающихся по математике позволяет делать выводы о

-знаниях, умениях и навыках по предмету ;

-логико-математических способностях ;

-степени развития общеобразовательных умений и навыков;

-результатах познавательной деятельности;

-результатах преподавания и управления учебно-воспитательным процессом. То есть, мониторинг качества математического образования школьников предусматривает:

-определённые качества овладения обучающимися программными знаниями и умениями на разных уровнях деятельности;

-выявление факторов, влияющих на качество математической подготовки обучающихся;

-изучение индивидуальных способностей и особенностей при проведении коррекционных мероприятий по предмету;

-исследования сформированности и адекватности самооценки обучающимися уровня своей подготовки по математике.

Мониторинг проводится в виде трех работ в течении года. Диагностической, семестровой и годовой или итоговой контрольных работ.

Диагностические контрольные работы, которые проводятся в сентябре имеют прогностический характер и предусматривают следующее:

- изучить уровень математической компетентности и готовность обучающихся к усвоения материала в рамках требований государственного стандарта;

- выявить уровень математической подготовки обучающихся для организации коррекционной работы и их самообразованию;

- сформировать базу для повышения уровня учебных достижений обучающихся; -на основе анализа результатов, составить мероприятия для оказания практической помощи учителям по повышению результативности педагогического труда и профессионального мастерства;

- направить учебно-воспитательный процесс на индивидуализацию и дифференциацию с целью развития каждой личности.

Изменения в программах по математике с 2014-2015 года повлекли за собой необходимость нового подхода к заданиям мониторинга по математике

Большое внимание мониторингу уделяется в так называемых «рубежных» классах:

-6 класс – итог изучения основ математики;

-9класс - итог изучения основ алгебры и планиметрии;

-11 класс – итог изучения алгебры, начала математического анализа и стереометрии в рамках школьной программы.

Но не менее важным является отслеживание и анализ результатов по математике в других классах. Так, например, ни для кого не секрет, что большую базу для изучения алгебры и геометрии в 9 классе закладывают в 5-8 классах. И очень важно не упустить момент, когда еще можно провести коррекционную работу, которая осуществляется на основе тематического учета знаний обучающихся и компетентного анализа, способствует устранению пробелов в знаниях обучающихся и совершенствованию их самообразовательной работы и развитию самоконтроля.

Таким образом становится вопрос о проблемах преемственности в и о внутренней взаимосвязи в сознании обучающихся усваиваемых знаний, умений и навыков, об осмысливании пройденного на новом, более высоком уровне, вопрос о результативности работы учителя с точки зрения качества усвоения учащимися преподносимого им учебного материала, о развитии целостной личности учащегося.

Раздел 3. Проблема преемственности в педагогике и методике математики

Общенаучная категория «преемственность» имеет объективный и всеобщий характер, проявляясь в природе, обществе и познании. Совре-менное состояние преемственности в обучении характеризуется разно-сторонностью охвата многих вопросов и неоднозначностью толкования отдельных понятий в данной области. Существует два подхода к рас-смотрению этой проблемы: в конкретном применении к сложнейшим педагогическим явлениям преемственность выступает как инструмент, позволяющий проникнуть в суть методических проблем, исследовать и управлять процессом обучения и воспитания, и в то же время сама является предметом целенаправленных и разнообразных исследований.

Педагогический и частнодидактический уровни преемственности раскрываются в работах Б. Г. Ананьева, В. А. Батаршева, П. Я. Гальперина, Ш. И. Ганелина, И. Д. Зверева, Л. Я. Зориной и других. Частнодидактический уровень предполагает рассмотрение преемственности как проявления дидактического принципа систематичности и последовательности. Известно, что взаимосвязь принципов преемственности, последовательности и систематичности была установлена еще в классической педагогике, где преемственность рассматривалась как самостоятельный принцип. В дидактике же всегда придавалось большое значение опоре нового материала на старые знания, на систему сложившихся связей, но в недостаточной степени учитывалось развитие старых знаний под влиянием новых. Когда при прохождении нового материала привлекаются старые знания, то они оживляются, становятся более мобильными и более совершенными, а новый материал, включаясь в уже сформировавшуюся систему знаний, лучше усваивается. Знания видоизменяются, совершенствуются, когда применяются в новых условиях. Как отмечает Б. Г. Ананьев: «Имеется двухсторонняя зависимость друг от друга новых знаний и старого опыта, которая проявляется в процессе систематизации знаний» .

Линейно-концентрическое построение школьного курса математики позволяет выделить два направления реализации преемственности в обучении предмету:

1) преемственность между смежными ступенями обучения;

2) преемственность внутри каждой ступени обучения:

а) преемственность внутри каждого курса математического характера (арифметики, алгебры, алгебры и начал анализа, геометрии);

б) преемственность между курсами математического характера, в частности, между пропедевтическими и систематическими курсами (например, алгеброй и геометрией, арифметикой и алгеброй, арифметикой и геометрией и др.).

В дидактике и методике преподавания математики отмечена особая роль повторения в осуществлении двусторонних преемственных связей нового и старого материала. Как известно, повторение материала пред-полагает мыслительные процессы: актуализацию, систематизацию, обоб-щение. Поэтому организация повторения учебного материала с целью его актуализации, обобщения и систематизации, может быть одним из ведущих путей осуществления преемственности в обучении математике.

Линейное построение курса математики позволяет выделить три этапа в организации повторения .

1. Обобщение и систематизация знаний, умений и навыков на каждом этапе обучения в рамках рассматриваемой содержательной линии. Выделение главного, организация его в систему. Установление соответствующих связей с другими содержательными линиями.

2. Повторение с целью актуализации соответствующей системы знаний, восстановление необходимых навыков решения задач перед каждым следующим этапом изучения материала данной содержательной линии.

3. После каждого этапа развития содержательной линии система знаний дополняется, вскрываются и устанавливаются внутренние связи, то есть организуется новая система знаний более высокого порядка.

Вместе с тем, целесообразно проведение обобщающих уроков по основным содержательным линиям в конце и начале каждого года обучения, что способствует систематизации материала и осознанию школьниками внутренней структуры курса математики.

Школьный курс алгебры развивает, углубляет и расширяет теорети-ческие сведения, приемы и методы решения задач, полученные учащимися на уроках математики в 5–9 классах. В связи с этим обеспечение преемствен-ности в обучении между курсами арифметики и алгебры занимает одно из важнейших мест в методике преподавания математики.

Раздел 4. Реализация преемственности через систематизацию и обобщение знаний

Средством реализации преемственности служит организация повторения с целью актуализации, обобщения и систематизации теорети-ческого материала и приемов решения задач на разных этапах изучения содержательной линии как внутри курса каждого класса, так и внутри ступени обучения.

C давних пор перед человечеством стоит проблема: чему учить и как учить. Целью воспитания и образования в нашем обществе является всесторонне развитая личность, т.е. формирование личности, обладающей высокими духовными потребностями. Это, в свою очередь, диктует необходимость так строить познавательную деятельность обучающихся на уроке и вообще весь учебный процесс, чтобы обеспечить развитие их творческой активности.

Изучение психологической литературы показывает, что задачам развития творческой активности обучающихся отвечает развивающее обучение, т.е. такое обучение, при котором формы, методы, приемы, средства преподавания направлены не только на усвоение знаний (умений, навыков), но и на интенсивное всестороннее развитие личности учащегося, овладение ими способами добывания знаний, развитие его творческой активности.

Современный учебный процесс рассматривается как активное взаимодействие учителя, с одной стороны, и обучающихся с другой, в ходе которого у них формируется определенная система знаний, умений, навыков, а также убеждений, составляющих мировоззрение. И если обучение математике построить на принципе обобщения и систематизации знаний, то оно будет удовлетворять всем принципам развивающего обучения.

Известно, что обобщение и систематизация - неотъемлемое свойство умственной деятельности, лежащее в основе установления существенных взаимосвязей между изучаемыми явлениями и научного познания вообще.

Последовательное осуществление систематизации - необходимое условие формирования обобщенных знаний, творчески применяемых в различных ситуациях. Обобщение знаний, в свою очередь, естественным образом предполагает их систематизацию.

Для школьного курса математики характерным является также то, что многие понятия не вводятся сразу в полном объеме и содержании. Содержание и объем таких понятий расширяются и обогащаются постепенно, по мере развития курса. Достаточно вспомнить понятие числа, функциональной зависимости, геометрические фигуры. Уже в начальных классах обучающихся индуктивным путем знакомят с этими понятиями. К моменту их изучения в систематических курсах алгебры и геометрии накапливается достаточно материала для их введения на основе систематизации и обобщения, предупрежда­ющих формальное усвоение знаний.

Объем информации, которую перерабатывает ученик в школе, растет. Увеличивается нагрузка на память ученика, а поскольку память и усвоение взаимосвязаны, то усвоение материала для значительной части школьников затрудняется. Нагрузка на произвольную память тем больше, чем меньше связаны между собой усваиваемые понятия. Отсюда следует, что усвоение большого количества информации за одну и ту же единицу времени возможно только на пути укрупнения единиц усвоения, т. е. на пути формирования теоретических обобщений и систематизации знаний. Этим создаются условия для объединения единичных многочисленных фактов и облегчается их усвоение и запоминание

Поэтому обобщение и систематизация знаний являются эффективным средством углубления, универсализации, упорядочения понимания и запоминания знаний. Множество внешне разрозненных фактов, явлений, примеров при нахождении общих принципов становится иллюстрацией этих общих положений, что не только способствует лучшему запоминанию и облегчению применения знаний, но и поднимает их на принципиально новый уровень. Появляется иной взгляд на мир, его законы. Именно обобщение фактов приводило в ряде случаев к выдающимся революционным открытиям не только в математике, но и в философии, истории, биологии, физике, химии и других науках

Раздел 5. Опыт работы. 5.1. Ведущая педагогическая идея.

Средством реализации преемственности служит организация повторения с целью актуализации, обобщения и систематизации теорети-ческого материала и приемов решения задач на разных этапах изучения содержательной линии как внутри курса каждого класса, так и внутри ступени обучения.

С повторения начинается учебный процесс в любом классе. Причем это не простое повторение, так как по-новому расставляются акценты, обучающиеся как бы поднимаются над известными фактами, и идет интенсивная пропедевтика нового материала. После проверки уровня знаний обучающихся (при необходимости после коррекции знаний) повторение плавно переходит в процесс усвоения новых знаний. Практически не бывает урока, на котором не было бы изучения новой темы. И если это не «голая» теория, то значит новые способы решения задач, новые связи между изучаемыми и уже изученными фактами, применение знаний в новых, незнакомых ситуациях.

Но как бы ни была насыщена программа, перед контрольной работой обязательно проводить урок обобщающего повторения. Необходимость организации обобщающего повторения обусловлена многими причинам: во-первых, неизбежен процесс забывания, приводящий к потере четкости, уменьшению объема знаний, к затруднениям и ошибкам. Во-вторых, особен-ность человеческого мышления такова, что даже простейшее восприятие и запоминание требует неоднократного обращения к материалу. В-третьих, повторение позволяет мне скоординировать свои действия по ликвидации пробелов в знаниях обучающихся.

Если обучать математике через обобщение и систематизацию, можно когда постоянные сравнения сходных объектов побуждают обучающихся проводить аналогии, искать связи с уже изученным материалом, а затем с помощью доказательств убеждаться в верности сделанного предположения или же простым примером опровергнуть только что выдвинутую гипотезу, то можно повысить познавательную деятельность обучающихся, развивать их творческую активность, а эти два фактора уже работают на развитие мышления.

5.2. Технология опыта

Я стараюсь так организовать обобщающее повторение, чтобы оно до-полняло полученные знания новыми сведениями, создавало предпосылку для более прочного закрепления и углубления всей системы знаний, а также формировало сознательное отношение к учебе, умение работать с учебной литературой, умение правильно организовывать свой труд.

Процесс обобщения выстраиваю так, чтобы изученный материал при этом переосмысливался в целом, что приводит не только к упрочнению усвоенного, но и к выстраиванию знаний в краткую структурную схему.

Систематическое целенаправленное использование обобщающего повторения помогает систематизировать знания, устраняет пробелы, успешно сдавать экзамены в школе и в вузах, успешно продолжать обучение.

Обобщенные знания более оперативны, легко актуализируются, т.е. возникают в памяти в нужный момент. На этом этапе проводится систематизация знаний и умений обучающихся, предполагающая сведение всего изученного в единый комплекс, выделение в нем главного и второстепенного, определение способов их взаимосвязи. Она необходима каждому ученику, поэтому работаю со всем классом, используя фронтальные формы учебной деятельности или работу в группах. В процессе этой работы знания и умения обучающихся группируются вокруг главного, стержневого момента учебного материала, образуя «островков» взаимосвязанных поня-тий, которые изучаются на протяжении ряда уроков, единый их блок, удоб-ный для запоминания и дальнейшего использования, дающий целостное видение изученного материала .

При подготовке к обобщающим урокам разрабатываю необходимый диагностический инструментарий для замера отслеживаемых качеств обучающихся, подбираю и разрабатываю сама задания развивающего характера. Мой опыт работы позволяет мне предложить для обобщения и систематизации знаний обучающихся в 8 классе варианта диагностической контроль-ной работы. Материал в заданиях контрольной работы подобран таким, образом, что каждый вариант включает в себя примеры и задачи изученные ранее в 5-7 классах, необходимость повторения которых продиктовано преемственностью тем 8 класса.

Был проведен тщательный анализ уже имеющихся разработок по этой тематике, а также использованы новые тенденции и подходы в разработке этой темы. Задания были подобраны с учетом разных уровней сложности, таким образом, чтобы были охвачены все изучаемые темы в каждом варианте. Уделено особое внимание тем темам 5-7 класса, опираясь на которые запланировано изучение новых тем в 8 классе. Так, например, разложение квадратного трехчлена на множители с использованием формул сокращенного умножения. Приведение многочлена к стандартному виду. Все эти приемы и навыки так или иначе используются в 8 классе при изучении тем: «Рациональные дроби», «Квадратные уравнения». А задания с исполь-зованием свойств степени с натуральным показателем в 7 классе, актуальны при изучении темы 8 класса : «Степень с целым показателем».

Закреплению и применению навыка решения уравнений способствует решение систем двух уравнений с двумя неизвестными. Итак, в курсе алгебры 7 класса получают развитие понятия, приемы и алгоритмы решения уравнений, рассмотренные в курсе арифметики. Основным объектом изучения являются уравнения первой степени с одним неизвестным, расширение сведений о которых происходит в тесной связи с развитием других содержательных линий курса. Однако данные уравнения являются основой и получают дальнейшее развитие при изучении алгебраического материала в 8 классе, где вводится новый вид уравнений – уравнения второй степени с одним неизвестным. Вместе с тем, теоретическая основа, многие приемы и алгоритмы выполнения основных операций с уравнениями являются сквозными. Выявление и осознание их общей структуры особенно важно для школьников, поскольку способствует определению перспективы в развитии уравнений, показывает преемственные связи материала и создает положительную мотивацию для его изучения. Навыки решения уравнений закрепляются при изучении арифметической и геометрической прогрессии, когда при решении задач на нахождение члена последовательности, номера члена прогрессии, знаменателя (разности), суммы и др. при помощи основных формул возникает необходимость решить уравнение. Основным материалом линии уравнений в 8 классе является знакомство с квадратным уравнением и способами его решения. Для этой темы характерна глубина изложения и богатство устанавливаемых с ее помощью связей в обучении, логическая обоснованность изложения. Поэтому она занимает особое место в линии уравнений и неравенств. К изучению темы обучающиеся приступают, накопив определенный запас алгебраических и общематематических представлений, понятий, умений. Этот материал во многом синтезирует материал, относящийся к уравнениям. Закрепление способов решения систем уравнений, рассмотренных в 7 классе, продолжается при решении систем, содержащих уравнение второй степени, что способствует формированию более прочных навыков.

Форма вариантов диагностической контрольной работы соответствует форме ГИА в 9 классе, с одним учетом, что количество времени предлагаемое для решения варианта уменьшено по сравнению с ГИА до 45 минут( 1 урок) . Кроме того часть заданий была непосредственно взята из контрольных комплексов заданий ГОСУДАРСТВЕННОЙ ИТОГОВОЙ АТТЕСТАЦИИ ПО МАТЕМАТИКЕ ПО ПРОГРАММАМ ОСНОВНОГО ОБЩЕГО ОБРАЗОВАНИЯ 2016-2017 учебного года.

Предлагаемое пособие предназначено для организации уроков обобщения и систематизации знаний и умений обучающихся в начале 8 класса. Это пособие может быть использовано для подготовки и проведения диагностической контрольной работы в 8 классе. Предлагается 10 вариантов контрольной работы по математике.

Диагностическая контрольная работа по алгебре в 8 классах, для тех, кто обучается по учебнику авторов: Ю.Н Макарычева, Г.Н. Миндюка,и др.

Каждый вариант состоит из трех частей, которые отличаются по сложности и форме содержания заданий.

В І части контрольной работы предложены пять заданий. Записывать следует только ответ. Правильный ответ оценивается одним баллом.

ІІ часть контрольной работы состоит из двух заданий. Решение может иметь краткую запись решения без обоснования. Правильное решение каждого задания этого блока оценивается двумя баллами.

ІІІ часть контрольной работы состоит из одного задания. Решение должно иметь развернутую запись с обоснованием. Правильное решение оценивается тремя баллами.

Сумма баллов начисляется за правильно выполненные задания в соответствии с максимально возможным количеством предложенных баллов для каждой части (всего 12 баллов).

При переводе в 5-и бальную систему оценивания предлагается следующая шкала перевода баллов в оценку:

11 - 12 баллов − «5»;

9 - 10 баллов − «4»;

6 - 8 баллов – «3»;

3 - 5 балла – «2»;

1 – 2 балла – «1».

Тексты заданий переписывать не обязательно, но необходимо указать номер варианта и номер задания.

5.3 Результативность

Систематизация и обобщение знаний и умений учащихся на основе преемственности– одно из основных условий повышения качества обучения. Умелое владение различными формами систематизации знаний и умений способствует повышению заинтересованности учащихся в изучении предмета, предупреждает отставание, обеспечивает активную работу каждого ученика.

Реальную картину уровня знаний учащихся можно получить проводя мониторинговые исследования. Их результаты помогают сделать выводы об успеваемости каждого моего ученика и своевременно корректировать педагогическое влияние.

Диаграммы результатов мониторинговых исследований

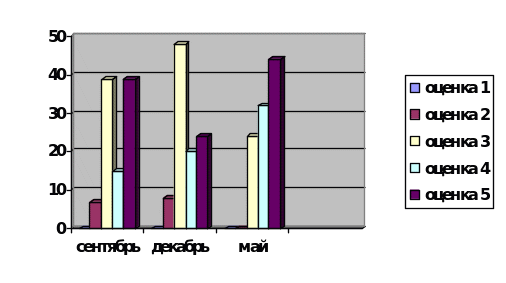Мониторинг уровня знаний обучающихся 8 классов по алгебре в 2016 - 2017 учебном году ( % )

Из полученных данных мы видим, что оценку «пять» получили в сентябре -39%, в мае – 44%,оценку «четыре» в сентябре-15%,а в мае-32%, ценку «три» в сентябре – 39%, в мае– 24; оценку «два» в сентябре-7%, в мае– 0%.

Результаты мониторинговых исследований показали, что в учащихся значительно возрос уровень знаний. Это было достигнуто благодаря проведению систематизации и обобщения полученных математических знаний на основе преемственности в обучении.

Результатами работы является успешное выступление моих обучающихся на районной и республиканской олимпиадах .

Выводы

Построение обучения на принципе обобщения и систематизации как одной из форм реализации преемственности в изучении математики позволяет ученикам увидеть предмет не как набор хаотически перемешанных фактов, никак не связанных между собой, а как стройную систему понятий, находящихся между собой в четко определенных отношениях. Установление логических связей, работа на базе сравнения, анализа, обобщения, конкретизации и т.д. позволяет не только углублять математические знания, но и оказывает огромное влияние на формирование процесса мышления обучающихся.

В своей работе использую как общепринятые формы систематизации, так и нетрадиционные формы, основываясь на идею преемственности в обучении математике. В результате проведения систематизации и обобщения знаний и умений как метода преемственности, раскрываются индивидуальные особенности детей, повышается уровень подготовки к уроку, что позволяет своевременно устранять недостатки и пробелы в знаниях обучающихся.

Таким образом, если систематически использовать такие формы систематизации и обобщения на уроках математики, то:

• расширяются и систематизируются представления школьников по предмету;

• формируются навыки самосистематизации и обобщения знаний.

Кропотлива и длительная подготовка и максимальное использование систематизации и обобщения как метода преемственности в обучении математике, окупится с лихвой. Анализ результативности подтверждает правильность выбранного направления.

Список литературы

1. Программы основного общего образования. Алгебра 7-9 класс. Донецк, 2016

2. Федченко Л.Я. Сборник заданий для тематических аттестаций . Алгебра 7-9 классы , Донецк, Каштан 2009.

3. Федченко Л.Я., Литвиненко Г.Н. Разноуровневые задания для тематических и итоговых контрольных работ. 7-8 классы, Донецк, 2004.

4. Макарычев Ю.Н., Миндюк Г.Н. Алгебра 7 класс М.: Просвещение 2013.

5. Письмо от 03.11.2016 года № 313/02 "О проведении мониторинга качества математического образования в образовательных организациях общего образования ДНР"

6. 6.Статья : «О мониторинге качества математического образования школьников в Донецкой области» , автор: Федченко Л.Я, журнал «Дидактика математики», ДНУ, Донецк, 2005

7. Калинина М.И. К вопросу о систематизации знаний обучающихся/ сб. статей, сост. Борчугова З. Г., Батий Ю. Ю. – М.: Просвещение, 2004.

8. Скаткина М.Н., Краевского М.Н. Качество знаний обучающихся и пути его совершенствования. – М.: Педагогика, 2003.

9. О совершенствовании методов обучения математики / Сб. статей сост. Крамор В. С. – М.: Просвещение, 2004.

10. Груденов Я. И. Совершенствование методики работы учителя математики – М: Просвещение, 2005.

11. Скобелев Г. Н. Систематизация знаний на уроках математики – Минск, 2006.

12. Виленкин Н.Я., Дудничев К.И., Калужнин Л.А. Современные основы школьного курса математики.– М.: Просвещение, 2004.

13. Иржавцева В.П., Федченко Л.Я. Систематизация и обобщение знаний обучающихся в процессе изучения математики. –Киев: Радянська школа,1988.-205с.

14. В.А. Далингер. Методика обобщающих повторений при обучении математике [Текст]: пособие для учителей и студентов. – Омск: изд-во ОГПИ. 1992. – 88 с.

15. .Методика преподавания математики в средней школе. Общая методика [Текст]: учеб. пособие для студентов пед. ин-ов / А.Я. Блох, Е.С. Канин; сост. Р.С. Черкасов, А.А. Столяр. – М.: Просвещение. 1985. – 336 с.

16. Методика преподавания математики в средней школе. Общая методика [Текст]: учеб. пособие для студентов физ. – мат. фак. пед. ин-ов / В.А. Оганесян, Ю.М. Колягин, Г.Л. Луканкин, В.Я. Саннинский. – М.: Просвещение. 1980. – 368 с.

17. Педагогика [Текст]: учеб. пособие для студентов пед. ин-ов / Ю.К. Бабанский, В.А. Сластенин, Н.А. Сорокин; под ред. Ю.К. Бабанского. 2 – е изд., доп. и перераб. – М.: Просвещение, 1988. – 479 с.

18. Педагогический энциклопедический словарь [Текст] / гл. ред. Б.М. Бим – Бад. – М: Большая Российская энциклопедия, 2002. – 528 с.

19. Пойа Д. Как решать задачу [Текст]: пер. с англ. / Д. Пойа. – М.: Учпедгиз, 1959. – 216 с.

20. Шаталов В.Ф. Точка опоры - М.: Педагогика, 1987. – 158 с.

21. Шаталов В.Ф. Куда и как исчезли тройки - М.: Просвещение, 2004.

16.Психологический словарь / под ред. В.В. Давыдова, А.В. Запорожца, Б.Ф. Ломова; науч. – исслед. ин-т общей и педагогической психологии АПН СССР. – М.: Педагогика, 1983. – 448 с.

17.Саранцев Г.И. Общая методика преподавания математики [Текст]: учеб. пособие для студентов мат. спец. пед. вузов и университетов / Г.И. Саранцев. – Саранск: Тип. «Крас. Окт.», 1999. – 208 с.

18.СеменовЕ.Е. Об одном приеме обучения обучающихся обобщению и конкретизации [Текст] / Е.Е. Семенов // Математика в школе. – 1976. №2. – С. 55 – 57.

19.Философская энциклопедия [Текст]. Т4.-М.:Современная энциклопедия, 1967. – 519 с.

20.Философский энциклопедический словарь [Текст].Т4.-М.:Современная энциклопедия, 1983. – 446 с.

21.Педагогическая энциклопедия. Москва: Советская энциклопедия, 1966

22.Вахламова А. П., Рабунский Е. С. О систематической взаимопроверке знаний обучающихся на уроках // Математика в школе, 2004. - №1.

Приложение.

Диагностическая контрольная работа по алгебре в 8 классах, для тех, кто обучается по учебнику авторов: Ю.Н Макарычева, Г.Н. Миндюка,и др.

Предлагаются задания по алгебре в 10 вариантах

Каждый вариант состоит из трех частей, которые отличаются по сложности и форме содержания заданий.

В І части контрольной работы предложены пять заданий. Записывать следует только ответ. Правильный ответ оценивается одним баллом.

ІІ часть контрольной работы состоит из двух заданий. Решение может иметь краткую запись решения без обоснования. Правильное решение каждого задания этого блока оценивается двумя баллами.

ІІІ часть контрольной работы состоит из одного задания. Решение должно иметь развернутую запись с обоснованием. Правильное решение оценивается тремя баллами.

Сумма баллов начисляется за правильно выполненные задания в соответствии с максимально возможным количеством предложенных баллов для каждой части (всего 12 баллов).

При переводе в 5-и бальную систему оценивания предлагается следующая шкала перевода баллов в оценку:

11 - 12 баллов − «5»;

9 - 10 баллов − «4»;

6 - 8 баллов – «3»;

3 - 5 балла – «2»;

1 – 2 балла – «1».

Контрольная работа проводится по расписанию согласно календарно- тематическому планированию в данном классе. При выполнении работы необходимо указать номер задания. Текст задания переписывать не обязательно. Примечание. В тексты заданий можно вносить коррективы: увеличить (уменьшить) количество заданий, усилить (ослабить) степень сложности или заменить текст задания в соответствии пройденной программы.

В – 1

І часть (5 баллов)

При выполнении заданий 1-5 следует записать только ответ. Верный ответ каждого задания оценивается одним баллом.

1.Вычислить: 2,6+3,4:1

Ответ: ______

2. Найдите значение выражения в точке: y= x+3, x₀=−16

Ответ: ______

3.Разложите на множители : x²−6х+9.

Ответ: ______

4. Найдите значение выражения: (−2)⁴

Ответ: ______

5. Из свежих груш получают 18%сушеных. Сколько взяли свежих груш, если получили 9 кг сушеных?

Ответ: ______

ІІ часть (4 балла)

Решение заданий 6 -7 может иметь краткую запись без обоснования. Правильное решение каждого задания оценивается двумя баллами...

6. Приведите подобные слагаемые: −15m⁷−3m⁴+m³+5+15m⁷+3m⁴−m³−5

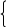
7. Решите систему уравнений: 2х+у=1,

х+3у=13.

ІІІ часть (3 балла)

Решение 8 задания должно иметь обоснование. Необходимо записать последовательные логические действия и объяснения. Правильное решение задания оценивается тремя баллами.

8. На первой стоянке в 4 раза меньше автомашин , чем на второй. После того как на первую стоянку приехали 35 автомашины, а со второй уехали 25, автомашин на стоянках стало поровну.

В – 2

І часть (5 баллов)

При выполнении заданий 1-5 следует записать только ответ. Верный ответ каждого задания оценивается одним баллом.

1. Отцу и сыну 75 лет. Каков возраст сына и отца, если отец в 2 раза старше сына?

Ответ: ______

2.Выполните действия((0,3)³)⁵:(0,3)¹³:

Ответ: ______

3.Вычислите: 30,05:0,5−1976: 32,5 .

Ответ: ______

4.Упростите выражение: 7ху²∙12х³у

Ответ: ______

5. На рисунке жирными точками показано суточное количество осадков выпавших с 7 по 18 декабря 2015 года. По горизонтали указываются числа месяца, по вертикали – количество осадков, выпавших в соответствующий день в миллиметрах. Для наглядности жирные точки на рисунке соединены линиями. Определите по рисунку, какого числа из данного периода выпало ровно1,5 миллиметров осадков.

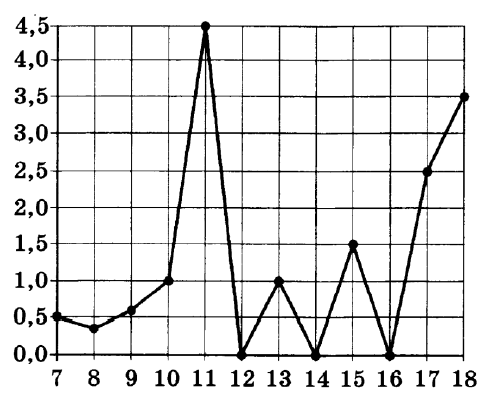
Ответ: ______

ІІ часть (4 балла)

Решение заданий 6 -7 может иметь краткую запись без обоснования. Правильное решение каждого задания оценивается двумя баллами...

6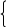 . Решите уравнение:

7. Решите систему уравнений: 4(2х−1)+5(3у−2)=40,

4(3х+1)=5(3у+2).

ІІІ часть (3 балла)

Решение 8 задания должно иметь обоснование. Необходимо записать последовательные логические действия и объяснения. Правильное решение задания оценивается тремя баллами.

8. Расстояние между городами состав прошел за 3,6 часа. Чтобы это же расстояние проехать за 3,5 часа его скорость увеличили на 1 км/ч. Найти расстояние между городами.

В – 3

І часть (5 баллов)

При выполнении заданий 1-5 следует записать только ответ. Верный ответ каждого задания оценивается одним баллом.

1.Является ли число 7 корнем уравнения 3х−6=х+8?

Ответ: ______

2.Вычислите: (26,2−30,5):

Ответ: ______

3.Запишите многочлен в стандартном виде: х²у+уху.

Ответ: ______

4. Сколько процентов часа составляют 42 минуты?

Ответ: ______

5. Выполните действия: ( ⁵ : ( ³

Ответ: ______

ІІ часть (4 балла)

Решение заданий 6 -7 может иметь краткую запись без обоснования. Правильное решение каждого задания оценивается двумя баллами...

6. Запишите в виде многочлена: (х+8)²+х(х+16)

7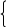 . Решите систему уравнений 3х−2у=−5,

х−2у=−5.

ІІІ часть (3 балла)

Решение 8 задания должно иметь обоснование. Необходимо записать последовательные логические действия и объяснения. Правильное решение задания оценивается тремя баллами.

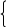
8. Постройте график функции: у= 3+2х если, х

3−2х, если, х 0

В – 4

І часть (5 баллов)

При выполнении заданий 1-5 следует записать только ответ. Верный ответ каждого задания оценивается одним баллом.

1. Запишите одночлен в стандартном виде:(4а²)³

Ответ: ______

2.Вычислите: 85²−15²

Ответ: ______

3. Сколько процентов составляет число 24 от числа 120?

Ответ: ______

4. Решите уравнение: 2х+7=17

Ответ: ______

5. Найдите сумму многочленов: а+3b и 3a−3b

Ответ: ______

ІІ часть (4 балла)

Решение заданий 6 -7 может иметь краткую запись без обоснования. Правильное решение каждого задания оценивается двумя баллами...

6. Вычислите : (1,75:

7. Выполни действия: (х+2)⁴:(х+2)³

ІІІ часть (3 балла)

Решение 8 задания должно иметь обоснование. Необходимо записать последовательные логические действия и объяснения. Правильное решение задания оценивается тремя баллами.

8. Подберите такие значения k и p, чтобы система имела одно решение

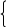2х+у=3,

kх+2у=p.

В – 5

І часть (5 баллов)

При выполнении заданий 1-5 следует записать только ответ. Верный ответ каждого задания оценивается одним баллом.

1.Упростить:(х−4) ² +3

Ответ: ______

2.Разложите на множители: 4х+4х²

Ответ: ______

3. Решите уравнение: 7,2+4х=7,2−х

Ответ: ______

4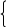 . Решите систему уравнений: х−у=0,

3х−у=2

Ответ: ______

5. Упростить:3(a−b)−3a

Ответ: ______

ІІ часть (4 балла)

Решение заданий 6 -7 может иметь краткую запись без обоснования. Правильное решение каждого задания оценивается двумя баллами...

6. Не выполняя построение найдите точки пересечения графика функции у=4х−8 с осями координат

7. Вычислите: (8⁰−2)∙(2,5⁷−3)⁰

ІІІ часть (3 балла)

Решение 8 задания должно иметь обоснование. Необходимо записать последовательные логические действия и объяснения. Правильное решение задания оценивается тремя баллами.

8. Вычислить:

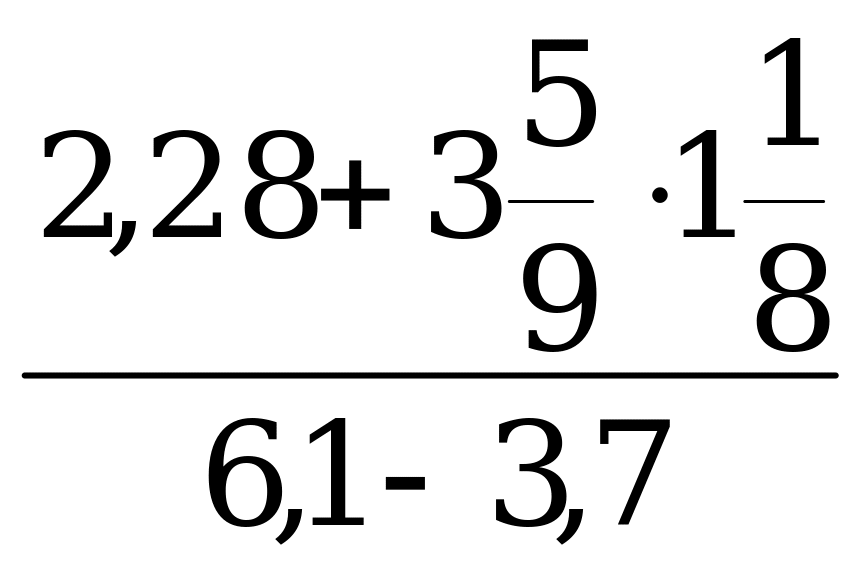
В – 6

І часть (5 баллов)

При выполнении заданий 1-5 следует записать только ответ. Верный ответ каждого задания оценивается одним баллом.

1. Вычислите: (5−3,75):1

Ответ: ______

2.Найдите точку пересечения графика у=−3х−7 с осью ОУ

Ответ: ______

3.Запишите одночлен в стандартном виде: (−1 a²b³)².

Ответ: ______

4. Решите уравнение:

Ответ: ______

5. На рисунке жирными точками показано суточное количество осадков, выпавших с 6 по 18 января 2016 года. По горизонтали указываются числа месяца, по вертикали – количество осадков, выпавших в соответствующий день в миллиметрах. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку, сколько дней из данного периода выпадало более 3 миллиметров осадков.

Ответ: ______

ІІ часть (4 балла)

Решение заданий 6 -7 может иметь краткую запись без обоснования. Правильное решение каждого задания оценивается двумя баллами...

6. Раскройте скобки и упростите выражение:

7. Решите уравнение: 0,9х −0,6(х −3) = 2(0,2х −1,3).

ІІІ часть (3 балла)

Решение 8 задания должно иметь обоснование. Необходимо записать последовательные логические действия и объяснения. Правильное решение задания оценивается тремя баллами.

8. Постройте график функции: у= 0,5x−3. Принадлежит ли графику функции точка А(−18;−12)? Пользуясь графиком функции промежуток , где y

В – 7

І часть (5 баллов)

При выполнении заданий 1-5 следует записать только ответ. Верный ответ каждого задания оценивается одним баллом.

1. Вычислите: .

Ответ: ______

2. Найдите уравнение: 7х + 2 = 3х – 6.

Ответ: ______

3. Решите систему уравнений: .

Ответ: ______

4. Упростите выражение: .

Ответ: ______

5. Для пополнения школьной библиотеки было потрачено 2400 руб., из которых 20% – на книги по математике. Сколько денег было потрачено на приобретение книг по математике?

Ответ: ______

ІІ часть (4 балла)

Решение заданий 6 -7 может иметь краткую запись без обоснования. Правильное решение каждого задания оценивается двумя баллами...

6. Вычислите: .

7. Решите уравнение: х(2x + 3) −5(2x² −3x) = −3x(2x + 2).

ІІІ часть (3 балла)

Решение 8 задания должно иметь обоснование. Необходимо записать последовательные логические действия и объяснения. Правильное решение задания оценивается тремя баллами.

8. Длина прямоугольника на 2 см больше его ширины. Если длину увеличить на 2 см, а ширину увеличить на 4 см, то площадь прямоугольника умвеличится на 40 см² . Найдите первоначальную длину и ширину прямоугольника.

В – 8

І часть (5 баллов)

При выполнении заданий 1-5 следует записать только ответ. Верный ответ каждого задания оценивается одним баллом.

1. Найдите дробь со знаменателем 48, равную дроби

Ответ: ______

2. Вычислите наиболее рациональным методом: .

Ответ: ______

3. Разложите на множители: .

Ответ: ______

4. Решите уравнение: 6х+(3х-2)=16.

Ответ: ______

5. Упростите выражение: .

Ответ: ______

.

ІІ часть (4 балла)

Решение заданий 6 -7 может иметь краткую запись без обоснования. Правильное решение каждого задания оценивается двумя баллами...

6. Докажите тождество:

7. Запишите одночлен в стандартном виде: .

ІІІ часть (3 балла)

Решение 8 задания должно иметь обоснование. Необходимо записать последовательные логические действия и объяснения. Правильное решение задания оценивается тремя баллами.

8. Найдите три последовательных целых числа, квадрат наименьшего из которых на 11 меньше произведения двух других.

В – 9

І часть (5 баллов)

При выполнении заданий 1-5 следует записать только ответ. Верный ответ каждого задания оценивается одним баллом.

1. Упростите выражение: (7x - 19y) - (18y - 3x) + (6x - 16y).

Ответ: ______

2. Вычислите наиболее рациональным методом:

;

Ответ: ______

3. Решите систему уравнений: .

Ответ: ______

4. Найдите значение выражения: .

Ответ: ______

5. Разложить на множители: а³+3а²b+3ab²+b³.

Ответ: ______

ІІ часть (4 балла)

Решение заданий 6 -7 может иметь краткую запись без обоснования. Правильное решение каждого задания оценивается двумя баллами...

6. Запишите в виде многочлена:

7. Не выполняя построений, найдите точки пересечения графиков уравнений:
5y – x = 6 и 3x - 7y = 6.

ІІІ часть (3 балла)

Решение 8 задания должно иметь обоснование. Необходимо записать последовательные логические действия и объяснения. Правильное решение задания оценивается тремя баллами.

8. Сумма цифр двузначного числа равна 12. Если к этому числу прибавить 18, то получим число, записаное теми же числами, но в обратном порядке. Найдите первоначальное число.

В – 10

І часть (5 баллов)

При выполнении заданий 1-5 следует записать только ответ. Верный ответ каждого задания оценивается одним баллом.

1. Одно натуральное число больше второго на 10. Относятся они как 12:11 . Найдите эти числа.

Ответ: ______

2. . Решите уравнение: у : 0,6 = 6 : 1,8.

Ответ: ______

3.Вычислите: (-2)⁴.

Ответ: ______

4. При каком значении переменной выражение не имеет смысла?

Ответ: ______

5. Запишите в виде многочлена: (3-х)(9+3х+х²)

Ответ: ______

ІІ часть (4 балла)

Решение заданий 6 -7 может иметь краткую запись без обоснования. Правильное решение каждого задания оценивается двумя баллами...

6. Выполни действия: _.

7. Постройте график функции: у = 2х-5. По графику найдите:

а) значения у, при котором х = -1;

б) значения х, если у = -1,6;

в) значения х, при которых функция принимает положительные значения.

ІІІ часть (3 балла)

Решение 8 задания должно иметь обоснование. Необходимо записать последовательные логические действия и объяснения. Правильное решение задания оценивается тремя баллами.

8. Вычислить: 101²-202∙81+81²

Ответы:

В-1 1.5,8 2.у=-1 3.(х-3)2 4.16 5.50 кг 6.0 7.(-1;5) 8.х=20	В-2 1.50 и 25 лет 2.0.09 3.-0,7 4.84х4у3 5.15 декабря 6.х=2 7.(3;2) 8.126 км	В-3 1.Да 2.-8,6 3.х2у+ху2 4.0,7 5.2,25 6.2х2+32х+64 7.(0;2,5) 8.график Y 3 -1,5 0 1,5 Х
В-4 1.64а6 2.7000 3.20% 4.х=5 5.4а 6.1,6 7.х+2 8.	В-5 1.х2-8х+19 2.4х(1+х) 3.х=0 4.(1;1) 5.-3b 6.(0;8) и (2;0) 7.-1 8.2	В-6 1. 2.(0;7) 3.1 а4b6 4.x=0 5.4 дня 6.-1,5t+153 7.x=44 8.точка А принадлежит графику, х (-∞;6) Y 6 0 x -3
В-7 1.9820 2.х=-2 3.(2;2) 4.-8а3b2 5.480 рублей 6.55 7.х=0 8.4 и 6 см	В-8 1. 2.456,789 3.(a-b)(3a+2b) 4.x=2 5.2x2+2y2 6.10=10 7. a21c18 8.3;4;5	В-9 1.16х-53у 2.104,8 3.(6;2) 4.2 5.(a+b)3 6.2x2+16x+16 7.(9;3) 8.57
В-10 1.120 и 110 2.у=2 3.16 4. х 6 5.27-х3 6. 7. а)у(-1)=-7 б)х=1,7 в)х (2,5;+∞) 8.400