ГОСУДАРСТВЕННОЕ АВТОНОМНОЕ ПРОФЕССИОНАЛЬНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
НОВОСИБИРСКОЙ ОБЛАСТИ
«БАРАБИНСКИЙ МЕДИЦИНСКИЙ КОЛЛЕДЖ»
Рассмотрено на заседании ЦМК
Протокол № ____от________________
Председатель_____________________

МЕТОДИЧЕСКАЯ РАЗРАБОТКА
ТЕОРЕТИЧЕСКОГО ЗАНЯТИЯ ДЛЯ ПРЕПОДАВАТЕЛЯ
Специальность 31.02.01 Лечебное дело
Дисциплина «Математика»
Раздел 1. Математический анализ
Тема 1.7. Основы интегрального исчисления. Определённый интеграл
Разработчик – преподаватель О.А. Потемкина
2020
Оглвление
Методический лист 3
Примерная хронокарта 6
Актуализация опорных знаний, проверка домашнего задания 7
Исходный материал 9
Задания для закрепления и систематизации новых знаний 15
ЗАДАНИЯ ДЛЯ ПРЕДВАРИТЕЛЬНОГО КОНТРОЛЯ ЗНАНИЙ 16
Контролирующий материал 16
Задание для самостоятельной внеаудиторной работы студентов 17
Список использованных источников 18
Выписка из рабочей программы дисциплины «Математика»
для специальности 31.02.01 Лечебное дело
| Наименование разделов и тем | Содержание учебного материала, лабораторные и практические работы, самостоятельная работа обучающихся, курсовая работа (проект) | Объем часов | Уровень освоения |
| 1 | 2 | 3 | 4 |
| Раздел 1. | Математический анализ | 48 |
|
| Тема 1.7. Основы интегрального исчисления. Определённый
интеграл | Содержание учебного материала | 2 |
|
| Основы интегрального исчисления. Криволинейная трапеция. Определённый интеграл. Свойства определённого интеграла. Формула Ньютона-Лейбница. Методы вычисления определённых интегралов. Применение определённого интеграла к решению прикладных задач в области профессиональной деятельности | 1,2 |
| Лабораторные работы | ‑ |
|
| Практические занятия 6) Определённый интеграл. Задачи, решаемые с использованием свойств первообразных и интегралов; 7) Вычисление площадей; 8) Вычисление объёмов. Механические и физические приложения определённого интеграла; 9) Итоговая работа по разделу «Математический анализ» |
2 2 2 2 |
|
| Контрольные работы | - |
| Самостоятельная работа обучающихся Выполнение упражнений. Работа с обучающими и контролирующими тестами на тему «Основы интегрального исчисления» Работа с учебником [1, стр. 88-114]; [1, стр. 116, задание №32, контрольные вопросы] | 5 |
Методический лист
Тип занятия – учебное занятие по изучению и первичному закреплению знаний и способов деятельности.
Вид занятия – вводная лекция.
Продолжительность – 90 мин.
ЦЕЛИ ЗАНЯТИЯ
Учебные цели:
сформировать знание об основах интегрального и дифференциального исчисления.
сформировать знание о значение математики в профессиональной деятельности и при освоении профессиональной образовательной программы;
сформировать знание об основных математических методах решения прикладных задач;
2. Развивающие цели:
способствовать развитию у студентов ОК 1. Понимать сущность и социальную значимость своей будущей профессии, проявлять к ней устойчивый интерес.
3. Воспитательные цели:
создать условия для формирования ОК 4. Осуществлять поиск и использование информации, необходимой для эффективного выполнения профессиональных задач, профессионального и личностного развития.
Методы обучения: объяснительно-иллюстративный, репродуктивный.
Место проведения занятия – аудитория колледжа.
Мотивация
Понятие интеграла является одним из основных в математике. К концу 17 в. Ньютоном и Лейбницем был создан аппарат дифференциального и интегрального исчисления, который составляет основу математического анализа. Изучение этой темы завершает школьный курс математического анализа, знакомит обучающихся с новым инструментом познания мира, а рассмотрение применения интегрального исчисления к важнейшим разделам физики показывает значение и силу высшей математики.
Определённый интеграл имеет большое практическое применение. С его помощью можно вычислять объёмы и площади поверхностей геометрических тел, длину кривой линии, площади плоских фигур, важные физические величины (работу, силу, теплоту и др.).
Необходимость полноценного изучения важнейших элементов интегрального исчисления связана с огромной значимостью и важностью этого материала при освоении профессиональной образовательной программы.
В дальнейшем вам пригодятся знание определённого интеграла при нахождении решения уравнений определяющих скорость радиоактивного распада, размножения бактерий, сокращении мышцы, растворении лекарственного вещества в таблетке и многих других задач дифференциального исчисления применяемых в медицинской практике, что будет способствовать формированию ОК 1. Понимать сущность и социальную значимость своей будущей профессии, проявлять к ней устойчивый интерес и ОК 4. Осуществлять поиск и использование информации, необходимой для эффективного выполнения профессиональных задач, профессионального и личностного развития.
Слайд 2
Сегодня оценка будет складываться из вашей работы в течении всего занятия.
На столах у вас лежит ЛИСТ САМООЦЕНКИ. Подпишите эти листы Ф.И.О.
| ЛИСТ САМООЦЕНКИ СТУДЕНТА |
| Ф.И.О |
| Вид оценки (диапазон баллов) | Пояснения к выставлению баллов | Количество баллов |
| Оценка за выполнение домашней работы (0-3 б) | Правильное решение: 2-х задач –3 балла, 1 задачи – 2 балла, решение задач с ошибками – 1 балл, отсутствие д/з – 0 баллов. | |
| Оценка за участие во фронтальном опросе (0-2 б) | Один правильный ответ – 1 балл, 2 ответа и более – 2 балла. | |
| Оценка за выступление или решение задачи у доски (1б) | Одно выступление или решение задачи у доски – 1 балл. | |
| Оценка за самостоятельную работу (3б) | Правильное решение задачи – 1 балл. | |
| Суммируйте все ваши баллы | |
| Максимально возможное количество баллов | 9 |
| Если ВЫ набрали 9 и выше баллов, поставьте оценку | 5 |
| Если ВЫ набрали 7-8 баллов, поставьте оценку | 4 |
| Если ВЫ набрали 5-6 баллов, поставьте оценку | 3 |
| Если ВЫ набрали 0-4 баллов, поставьте оценку | 2 |
| Ваша оценка |
|
Примерная хронокарта
| п/№ | Наименование этапа | Время | Цель этапа | Деятельность | Оснащение |
| преподавателя | студентов |
| -1- | -2- | -3- | -4- | -5- | -6- | -7- |
| Организационный этап | 1 | Организация начала занятия, формирование способности организовывать собственную деятельность (ОК1) | Отмечает отсутствующих студентов в журнале | Староста называет отсутствующих студентов. Студенты приводят в соответствие внешний вид, готовят рабочие места. | Журнал, тетради для конспектов и т.д. |
| Контроль знаний по предыдущей теме «Основы интегрального исчисления. Неопределённый интеграл» | 10 | Оценка уровня сформированности знаний по теме «Основы инте-грального исчис-ления. Неопределённый интеграл» | Инструктирует и проводит контроль | Дают письменный ответ на контрольные вопросы и решают примеры | МР стр. |
| Мотивационный этап и целеполагание | 1 | Развитие интереса к будущей профессии, понимания сущности и социальной значимости (ОК 1), установка приоритетов при изучении темы. Формирование знаний о значение математики в профессиональной деятельности и при освоении профессиональной образовательной программы; | Объясняет студентам важность изучения данной темы, озвучивает цели занятия | Слушают, задают вопросы, записывают новую тему | МР. |
| Изложение исходной информации | 35 | Формирование знаний: понимания сущности и социальной значимости своей будущей профессии (ОК 1), о основах интегрального и дифференциального исчисления, о основных математических методах решения прикладных задач; | Излагает новый материал | Слушают, читают материал на слайдах, записывают | Методическая разработка теоретического занятия, презентация, мультимедийная установка |
| Выполнение заданий для закрепления знаний | 35 | Закрепление, систематизация, обобщение знаний | Инструктирует и контролирует выполнение заданий, отвечает на вопросы студентов | Выполняют задания, слушают правильные ответы после выполнения, вносят коррективы, задают вопросы | МР стр. |
| Предварительный контроль новых знаний | 5 | Оценка эффективности занятия и выявление недостатков в новых знаниях | Инструктирует и проводит контроль | Выполняют задания | МР стр. |
| Подведение итогов занятия | 1 | Оценивает работу группы в целом. Объявляет оценки, мотивирует студентов, выделяет наиболее подготовленных | Слушают, участвуют в обсуждении, задают вопросы | Развитие эмоциональной устойчивости, дисциплинированности | Журнал |
| Задание для самостоятельной внеаудиторной работы студентов | 2 | Формирование и закрепление знаний | Дает задание для самостоятельной внеаудиторной работы студентов, инструктирует о правильности выполнения, критериях оценивания | Записывают задание | МР стр. |
Слайд 3-11
Актуализация опорных знаний, проверка домашнего задания
Мозговой штурм
(Фронтальный опрос. Вопросы и правильные ответы последовательно
высвечиваются на экране в виде слайдов)
| Вопрос | Ответ |
Что называется неопределённым интегралом? | Совокупность первообразных для функции f(x) называется неопределенным интегралом и обозначается символом  . . |
Назовите все элементы равенства 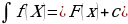 | Элементы неопределённого интеграла: f(x) — подынтегральная функция; f(x)dx- подынтегральное выражение; F(x) — искомая, называемая первообразной, функция; С — произвольная постоянная.
|
Сформулировать 1 свойство неопределённого интеграла. |  = a = a
|
Сформулировать 2 свойство неопределённого интеграла. | 
|
Сформулировать 3 свойство неопределённого интеграла. | 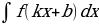 = =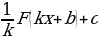
|
Если функция задается в виде многочлена третей степени, то какую степень имеет производная этой функции? А первообразная? | Вторую, четвёртую
|
Для какой функции её производная и первообразная совпадает с самой функцией? | ех
|
Производные каких функций равны 1, x, x2?
| 
|
Какая из двух функций является первообразной другой: 5x4 и x5+11? Почему? | x5+11 первообразная для 5x4, т.к. (x5+11)’=5x4 |
Является ли функция F(x)=Ctg(x) первообразной для функции f(x)=  на R? на R? | ДА |
Какие из равенств записаны неверно: �� 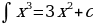 ; ; ��  ? В чём ошибка? ? В чём ошибка? | Первое, отсутствует dx в подынтегральном выражении |
Как проверить результаты интегрирования? | Продифференцировать полученное выражение |
Продолжи формулу:  | 
|
Продолжи формулу: 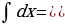 | 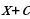
|
Продолжи формулу: 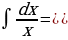 | 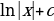
|
Продолжи формулу:  |  |
Продолжи формулу: 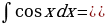 | 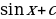
|
Продолжи формулу: 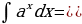 | 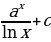
|
Перечислить основные методы интегрирования | Непосредственное интегрирование, замена переменной, по частям |
Графики, изображенные на рисунке, разбейте на пары «функция – ее первообразная» | а - д, д - б, и - к, ж – г. |
Кто желает оформить на доске своё решение домашних задач?
Исходный материал
План
Понятие определенного интеграла
Основные свойства определенного интеграла
Формула Ньютона–Лейбница
Методы решения определённого интеграла
Применение определенного интеграла к вычислению различных величин
Понятие определённого интеграла
Слайд 12
Интеграл, интегрирование, интеграция... Однокоренные слова, к тому же вышедшие за пределы математики и ставшие обиходными. В газетах читаем об интеграции наук, культур, в политике и экономике ведут речь об интегральных процессах.
Любопытно, что идеи интегрального исчисления возникли задолго до появления идей дифференциального исчисления. Греческие математики Эвдокс и Архимед (4; 3 века до н.э.) для решения задач вычисления площадей и объемов придумали разбивать фигуру на бесконечно большое число бесконечно малых частей и искомую площадь (объем) вычисляли как сумму площадей (объемов) полученных элементарных кусочков.
Слайд 13
Галилей, Кавальери, Торричелли, Ферма, Паскаль, Барроу ...
Слайд 14
Во второй половине 17 века идеи, подготовленные всем предшествующим развитием математики, были гениально осознаны, обобщены и приведены в систему английским физиком и математиком И. Ньютоном и немецким математиком В.Г. Лейбницем. Они создали стройную систему понятий и выработали правила, по которым можно вычислять интегралы.
Слайд 15
Понятие интеграла связано с обратной задачей дифференцирования функции. Понятие определенного интеграла удобно рассматривать на решении задачи о вычислении площади криволинейной трапеции.
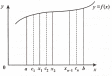
Для нахождения площади фигуры, ограниченной с двух сторон перпендикулярами, восстановленными в точках а и b, сверху непрерывной кривой у = f(х) и снизу осью Ох, разобьем отрезок [а, b] на небольшие отрезки:
a = x0x1x2...xn-1xn=b.
Восстановим перпендикуляры из этих точек до пересечения с кривой у = f(х). Тогда площадь всей фигуры будет примерно равна сумме элементарных прямоугольников, имеющих основание, равное хi = хi -хi-1, а высоту, равную значению функции f(х) внутри каждого прямоугольника. Чем меньше величина хi, тем точнее будет определяться площадь фигуры S. Следовательно:
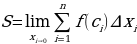
Слайд 16
Определение. Если существует предел интегральной суммы, не зависящий от способа разбиения отрезка [а, b] и выбора точек  , то этот предел называют определенным интегралом от функции f(х) на отрезке [а, b] и обозначают:
, то этот предел называют определенным интегралом от функции f(х) на отрезке [а, b] и обозначают:

где f(x) ‑ подынтегральная функция, х ‑ переменная интегрирования, а и b — пределы интегрирования (читается: определенный интеграл от a дo b эф от икс де икс).
Таким образом, геометрический смысл определенного интеграла связан с определением площади криволинейной трапеции, ограниченной сверху функцией у = f(х), снизу осью Ох, а по бокам ‑ перпендикулярами, восстановленными в точках а и b.
Процесс вычисления определенного интеграла называют интегрированием. Числа а и b называют соответственно нижним и верхним пределами интегрирования.
Слайд 17
Свойства определенного интеграла
Если пределы интегрирования равны, то определенный интеграл равен нулю:

Если переставить пределы интегрирования, то знак интеграла изменится на противоположный:
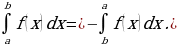
Постоянный множитель можно выносить за знак определенного интеграла:
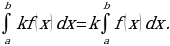
Определенный интеграл от суммы конечного числа непрерывных функций f1(x), f2(x)...fn(x), заданных на отрезке [а, b], равен сумме определенных интегралов от слагаемых функций:
Отрезок интегрирования можно разбивать на части:

Если функция всегда положительна, либо всегда отрицательна на отрезке [а, b], то определенный интеграл представляет собой число того же знака, что и функция:
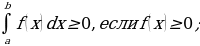
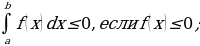
Слайд 18
Формула Ньютона-Лейбница
Формула Ньютона-Лейбница устанавливает связь между определенным и неопределенным интегралами.
Теорема. Величина определенного интеграла от функции f(х) на отрезке [а, b] равна приращению любой из первообразных для этой функции на данном отрезке:

Из этой теоремы следует, что определенный интеграл есть число, в то время как неопределенный ‑ совокупность первообразных функций. Таким образом, согласно формуле для нахождения определенного интеграла необходимо:
1. Найти неопределенный интеграл от данной функции, положив С = 0.
2. Подставить в выражение первообразной вместо аргумента х сначала верхний предел b, затем нижний предел а, и вычесть из первого результата второй.
Слайд 19
Методы вычисления определённого интеграла
При вычислении определенных интегралов используют методы, рассмотренные для нахождения неопределенных интегралов.
Метод непосредственного интегрирования
Этот метод основан на использовании табличных интегралов и основных свойств определенного интеграла.
ПРИМЕРЫ:
1) Найти 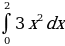
Решение: 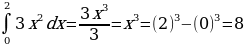
2) Найти 
Решение:
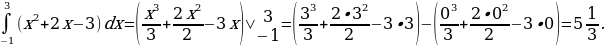
3) Найти 
Решение:
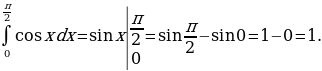
Метод замены переменной интегрирования
ПРИМЕР:
Найти 
Решение. Для нахождения интеграла воспользуемся методом замены переменной. Вводим новую переменную
u=3x ‑ 1, тогда du = 3dx, dx =  . При введении новой переменной необходимо осуществить замену пределов интегрирования, так как новая переменная будет иметь другие границы изменения. Они находятся по формуле замены переменной. Так верхний предел будет равен иb = 3
. При введении новой переменной необходимо осуществить замену пределов интегрирования, так как новая переменная будет иметь другие границы изменения. Они находятся по формуле замены переменной. Так верхний предел будет равен иb = 3 2 ‑ 1 = 5, нижний ‑ иа =3
2 ‑ 1 = 5, нижний ‑ иа =3 1 ‑ 1 = 2. Заменив переменную и пределы интегрирования, получим:
1 ‑ 1 = 2. Заменив переменную и пределы интегрирования, получим:
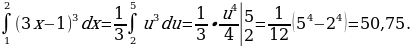
Метод интегрирования по частям
Этот метод основан на использовании формулы интегрирования по частям для определенного интеграла:

ПРИМЕР:
1) Найти 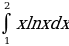
Решение:
Пусть u = ln x, dv = xdx, тогда 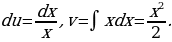
Отсюда
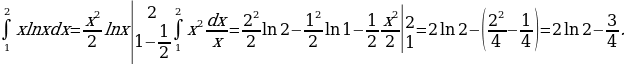
Слайд 20
Применение определенного интеграла к вычислению различных величин
Вычисление площади плоской фигуры
Ранее было показано, что определенный интеграл можно использовать для вычисления площади фигуры, заключенной между графиком функции у = f(x), осью Ох и двумя прямыми х = а и х = b.
Если функция у = f(x) находится ниже линии абсцисс, т.е. f(x) 
Если функция у = f(x) несколько раз пересекает ось Ох, то необходимо отдельно найти площади для участков, когда f(x) 0, и сложить их с абсолютными величинами площадей, когда функция f(x)
ПРИМЕР 1. Найти площадь фигуры, ограниченной функцией у = sin х и осью Ох на участке 0 х 2 .
.
Решение. Площадь фигуры будет равна сумме площадей:
S = S1 + |S2|,
где S1 —;площадь при у0; S2 — площадь при у 0.
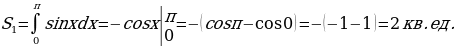
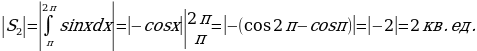
S=2 + 2 = 4 кв.ед.

ПРИМЕР 2. Найти площадь фигуры, заключенной между кривой у = х2, осью Ох и прямыми х = 0, х = 2.
 Решение. Построим графики функций у = х2 и х = 2.
Решение. Построим графики функций у = х2 и х = 2.
Заштрихованная площадь и будет искомой площадью фигуры. Так как f(x) 0,то

Слайд 21
Вычисление длины дуги плоской кривой
Если кривая у = f(х) на отрезке [а, b] имеет непрерывную производную, то длина дуги этой кривой находится по формуле:
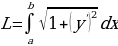
ПРИМЕР
Найти длину дуги кривой y2 = x3/2 на отрезке [0,1] (y0)
Решение
Уравнение кривой y = x3/2, тогда y’ = 1,5 x1/2.
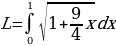
Сделав замену 1+ получим:
получим:
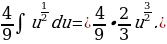
Вернёмся к первоначальной переменной:

Слайд 22
Вычисление объёма тела вращения
Если криволинейная трапеция, ограниченная кривой у = f(x) и прямыми х=а и х=b, вращается вокруг оси Ох, то объём вращения вычисляется по формуле:
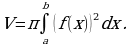
ПРИМЕР
Найти объём тела, образованного вращением вокруг оси Ох полуволной синусоиды
y= sin x, при 0≤ х≤ .
.
Решение
Согласно формуле имеем:

Для вычисления этого интеграла сделаем следующие преобразования:
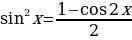
Тогда

Слайд 23
Задания для закрепления и систематизации новых знаний
1. Вычисление определённых интегралов
Слайд 24
2. Приложения определённого интеграла
Площадь фигуры
Вычислите площадь фигуры, ограниченной линиями:
 ;
;
 ;
;
 ;
;
 .
.
Путь, пройденный телом (точкой) при прямолинейном движении за промежуток времени от t1 до t2 (
Скорость движения точки изменяется по закону v =3t2 +2t -1 (t в с, v в м/с). Найдите путь, пройденный телом за 10с от начала движения.
Скорость движения точки изменяется по закону v =6t2 +4 (t в с, v в м/с). Найдите путь, пройденный точкой за 5с от начала движения.
Скорость движения точки v =12t -3t2 (t в с, v в м/с). Найдите путь, пройденный точкой от начала движения до её остановки.
Два тела начали двигаться одновременно из одной точки в одном направлении по прямой. Первое тело движется со скоростью v =6t2 +2t (м/с), второе v =4t+5 (м/с). На каком расстоянии друг от друга они окажутся через 5с?
ЗАДАНИЯ ДЛЯ ПРЕДВАРИТЕЛЬНОГО КОНТРОЛЯ ЗНАНИЙ Контролирующий материал
| Вариант 1 Выберите первообразную для функции  

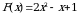
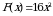
Найдите общий вид первообразных для функции 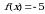 . . 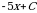



Решением интеграла 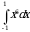 является число …. является число ….  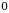  
| Вариант 2 Выберите первообразную для функции  . . 



Найдите общий вид первообразных для функции  . . 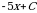



Решением интеграла  является число ….. является число ….. 
 

|
Эталона ответов:
| Вариант | 1 | 2 | 3 |
| 1 | В | А | А |
| 2 | Б | Г | А |
Критерии оценки
«5» - три верных ответа;
«4» - два верных ответа;
«3» - один верный ответ;
«2» - нет верных ответов.
Слайд 25
Задание для самостоятельной внеаудиторной работы студентов
1. Вычислите интегралы
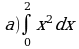

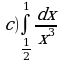

2. Вычислите площадь фигуры ограниченной линиями
y = - x2 + x + 6 и y = 0
Скорость движения точки изменяется по закону v =9t2 -8t (t в с, v в м/с). Найдите путь, пройденный телом за четвёртую секунду от начала движения.
Эталона ответов:
 ;
; 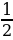 ; -1,5;
; -1,5; 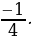
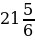 ;
;

Критерии оценки
«5» - шесть верных ответов;
«4» - пять-четыре верных ответа;
«3» - три-два верных ответа;
«2» - нет верных ответов.
Слайд 26
Список использованных источников
Гилярова М.Г. Математика для медицинских колледжей. – Ростов н/Д: Феникс, 2011. – 410, [1] с. – (Медицина)
Задачи, которые приводят к понятию определенного интеграла Римана [Электронный ресурс] / ib.mazurok.com - Режим доступа: http://ib.mazurok.com/2013/05/18/задачи-которые-приводят-к-понятию-опр/
Математика: учеб. пособие / В.С. Михеев [и др.]; под ред. Н.М. Демина. – Ростов н/Д : Феникс, 2009. – 896 с. – (Среднее профессиональное образование).








 .
.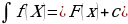
 = a
= a
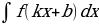 =
=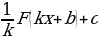

 на R?
на R?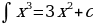 ;
;  ? В чём ошибка?
? В чём ошибка?

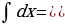
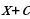
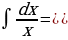
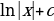


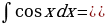
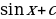
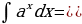
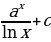

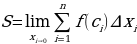
 , то этот предел называют определенным интегралом от функции f(х) на отрезке [а, b] и обозначают:
, то этот предел называют определенным интегралом от функции f(х) на отрезке [а, b] и обозначают:

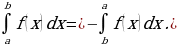
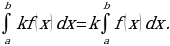

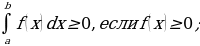
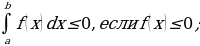

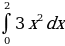
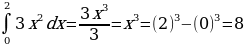

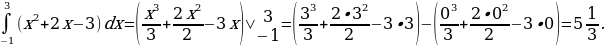

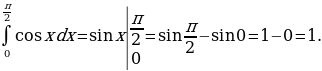

 . При введении новой переменной необходимо осуществить замену пределов интегрирования, так как новая переменная будет иметь другие границы изменения. Они находятся по формуле замены переменной. Так верхний предел будет равен иb = 3
. При введении новой переменной необходимо осуществить замену пределов интегрирования, так как новая переменная будет иметь другие границы изменения. Они находятся по формуле замены переменной. Так верхний предел будет равен иb = 3 2 ‑ 1 = 5, нижний ‑ иа =3
2 ‑ 1 = 5, нижний ‑ иа =3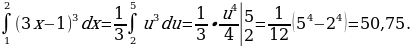

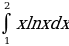
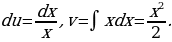
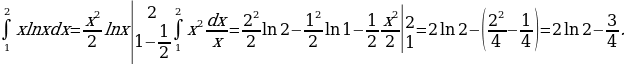

 .
.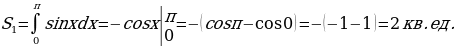
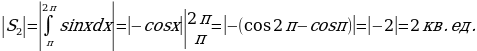

 Решение. Построим графики функций у = х2 и х = 2.
Решение. Построим графики функций у = х2 и х = 2.
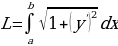
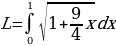
 получим:
получим: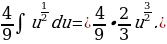

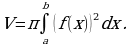

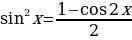

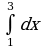 ;
; ;
;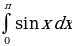 ;
; ;
;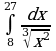 ;
;




 ;
; ;
; ;
; .
.



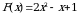
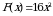
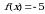 .
.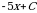



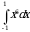 является число ….
является число …. 
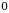


 .
.



 .
. является число …..
является число …..



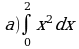

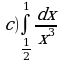

 ;
; 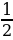 ; -1,5;
; -1,5; 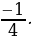
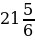 ;
;


















