СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока

МУ по ПЗ цикла МОЕН
Просмотр содержимого документа
«МУ по ПЗ цикла МОЕН»
Министерство общего и профессионального образования Ростовской области
Государственное бюджетное образовательное учреждение
среднего профессионального образования Ростовской области
«Сальский аграрно-технический колледж»
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
ПО ВЫПОЛНЕНИЮ
ПРАКТИЧЕСКИХ ЗАНЯТИЙ
По дисциплине ЕН.01 Математика
для специальности 38.02.01Экономика и бухгалтерский учет (по отраслям).
Гигант
2022
| Рассмотрено на заседании предметной (цикловой) комиссией математических и общих естественнонаучных дисциплин Протокол № ___ от ________ 20___г Председатель:_______ Кудрявцева Е.П. | «УТВЕРЖДАЮ» Зам. директора по учебной работе ___________________ И.А. Хара «___»_________________ 20 _ г. |
| Рассмотрено на заседании предметной (цикловой) комиссией математических и общих естественнонаучных дисциплин Протокол № ___ от ________ 20 ___г Председатель:_______ Кудрявцева Е.П. | «УТВЕРЖДАЮ» Зам. директора по учебной работе ___________________ И.А. Хара «___»_________________ 20 _ г. |
Автор: Ромащенко Т.А.
Рецензент: Калашникова Г.И.
АННОТАЦИЯ
на «Методические указания по выполнению практических занятий»
по дисциплине «Математика» для специальности:
38.02.01 Экономика и бухгалтерский учет (по отраслям).
Автор: Ромащенко Т.А., преподаватель дисциплины «Математика».
Адрес учебного заведения: Ростовская обл., Сальский р-н, п. Гигант, ул. Крупской,6.
«Методические указания» включают в себя:
оглавление;
предисловие;
содержание методических указаний;
правила выполнения ЛПЗ;
практические занятия № 1 – 17;
литературу.
Настоящий сборник ПЗ предназначен в качестве методического пособия для проведения практических занятий по программе дисциплины «Математика».
Методические указания содержат теоретический материал, необходимый по ходу выполнения работы, формулы, условия задач (к практическим занятиям), порядок выполнения ПЗ, требования к технике безопасности. В каждой работе содержатся вопросы для допуска к работе и для защиты работы, по её завершению.
Настоящий сборник может быть использован в качестве основного или дополнительного материала при проведении ПЗ.
ОГЛАВЛЕНИЕ
| Предисловие |
| Содержание методических указаний |
| Правила выполнения ПЗ |
Практическая работа № 1
Практическая работа № 2
Практическая работа № 3
Практическая работа № 4
Практическая работа № 5
Практическая работа № 6
Практическая работа № 7
Практическая работа № 8
Практическая работа № 9
Практическая работа № 10
Практическая работа № 11
Практическая работа № 12
Практическая работа № 13
Практическая работа № 14
Практическая работа № 15
Практическая работа № 16
Практическая работа № 17
Литература
ПРЕДИСЛОВИЕ
Назначение методических указаний
Настоящий сборник ПЗ предназначен в качестве методического пособия для проведения практических работ по программе дисциплины «Математика». Данный материал содержит описания практических работ:
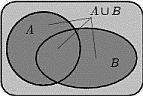
Решение задач с комплексными числами. Геометрическая интерпретация комплексного числа.
Действия над матрицами.
Определители второго и третьего порядков.
Формулы Крамера (для систем линейных уравнений с тремя неизвестными.)
Метод обратной матрицы
Решение матричных уравнений
Графический метод решения задачи линейного программирования.
Производная функции. Частные производные функции нескольких переменных.
Нахождение неопределённого интеграла с помощью таблиц, а также используя его свойства.
Методы замены переменной и интегрирования по частям.
Интегрирование простейших рациональных дробей.
Правила замены переменной и интегрирования по частям.
Вычисление несобственных интегралов. Исследование сходимости (расходимости) интегралов.
Приложения интегрального исчисления.
Дифференциальные уравнения первого порядка и первой степени.
Уравнения с разделяющимися переменными.
Однородное дифференциальное уравнение.
СОДЕРЖАНИЕ МЕТОДИЧЕСКИХ УКАЗАНИЙ
тема, наименование работы;
цель работы, требования к умениям и навыкам;
методические указания (практические работы)
задание.
ТРЕБОВАНИЯ К ЗНАНИЯМ И УМЕНИЯМ ПРИ ВЫПОЛНЕНИИ ПРАКТИЧЕСКИХ РАБОТ
В результате выполнения ПЗ, предусмотренных программой по данной специальности, студент должен:
знать:
значение математики в профессиональной деятельности и при освоении профессиональной образовательной программы;
основные математические методы решения прикладных задач в области профессиональной деятельности;
основные понятия и методы математического анализа, дискретной математики, линейной алгебры, теории комплексных чисел, теории вероятностей и математической статистики;
основы интегрального и дифференциального исчисления.
уметь:
решать прикладные задачи в области профессиональной деятельности.
ПРАВИЛА ВЫПОЛНЕНИЯ ПЗ
Студент должен прийти на практическое занятие подготовленным к выполнению работы. Студент, не подготовленный к работе, не может быть допущен к ее выполнению.
Каждый студент после выполнения работы должен представить отчет о проделанной работе, содержание которого определено в конце каждой работы.
Отчет о проделанной работе следует выполнять в тетради для практических работ.
Чертежи и схемы, необходимые для выполнения работы, следует выполнять карандашом с помощью чертежных инструментов (линейки, циркуля и т.д.).
Вычисления производить с точностью до двух значащих цифр.
Если студент не выполнил практическую работу или часть работы, то он может выполнить работу или оставшуюся часть во внеурочное время, согласованное с преподавателем.
Оценку по практической работе студент получает с учетом срока выполнения работы, если:
- задачи решены правильно и в полном объеме;
- студент может пояснить выполнение любого этапа работы;
- отчет выполнен в соответствии с требованиями к выполнению работы;
- грамотно, чётко и ответил на контрольные вопросы к защите работы.
В случае отсутствия на занятиях при выполнении практической работы, студент должен:
- получить указания у преподавателя;
- выполнить работу во внеурочное время согласно методическому указанию.
Зачет по работе студент получает при условии выполнения всех предусмотренных программой работ после сдачи отчетов по работам.
Практическое занятие № 1.
Решение задач с комплексными числами. Геометрическая интерпретация комплексного числа.
Цель: Продолжить формирование умения применять приемы сравнения, обобщения, и навыки воображения учащихся при работе с понятием комплексного числа.
Требования к умениям и навыкам.
Должен знать: Определение, свойства вероятностей событий, сумму и произведение вероятностей событий; определение вариационных рядов и основные числовые характеристики вариационных рядов.
Должен уметь: Применять теоретические знания при решении практических задач.
Задание: 1. Изучить методические указания к работе, записать указанные примеры с решениями.
2. Выполнить самостоятельную работу по вариантам.
3. Сделать отчёт.
Методические указания.
Краткие теоретические сведения.
Понятие комплексного числа
Задачи, приводящие к понятию комплексного числа
Решение квадратных уравнений
Одна из причин введения комплексных чисел состояла в том, чтобы добиться разрешимости любого квадратного уравнения, в частности уравнения
x2 = – 1.
Покажем, что расширив поле действительных чисел до поля комплексных чисел, мы получили поле, в котором каждое квадратное уравнение разрешимо, т.е. имеет решение. Так, уравнение x2 = – 1 имеет два решения: x1 = i, x2 = – i.
Это нетрудно установить проверкой: i•i = i2 = – 1, (– i)•(– i) = i2 = – 1.
Действительные числа можно изобразить точками прямой линии, как показано на рисунке, где точка A изображает число 4, а точка B число -5. Эти же числа можно изображать также отрезками OA, OB, учитывая не только их длину, но и направление.
Каждая точка M числовой прямой изображает некоторое действительное число (рациональное, если отрезок OM соизмерим с единицей длины, и иррациональное если несоизмерим). Таким образом, начисловой прямой не остается места для комплексных чисел.
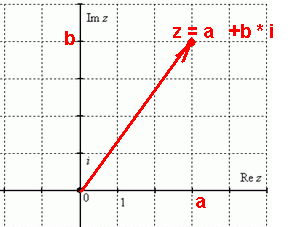
Но комплексные числа можно изображать на числовой плоскости. Для этого мы выбираем на плоскости прямоугольную систему координат, с одинаковым масштабом на обеих осях.
Комплексное число a + b·i изображается точкой M, у которой абсцисса x равна абсциссе a комплексного числа, а ордината y равна ординате b комплексного числа.
Множество действительных чисел содержит и целые числа, и дроби, и иррациональные числа. При этом каждой точке числовой прямой обязательно соответствует некоторое действительное число.
Прежде чем, мы перейдем к рассмотрению комплексных чисел, заметим,:: не пытайтесь представить комплексное число «в жизни» – это всё равно, что пытаться представить четвертое измерение в нашем трехмерном пространстве.
Если хотите, комплексное число – это двумерное число. Оно имеет вид : Z = a + bi
где a и b – действительные числа, i – так называемая мнимая единица. Число ![]() называется действительной частью
называется действительной частью
(Re Z) комплексного числа Z, число b называется мнимой частью
(Im Z) комплексного числа Z.
– это ЕДИНОЕ ЧИСЛО, а не сложение. Действительную и мнимую части комплексного числа, в принципе, можно переставить местами:
Z= a+ ib
или переставить мнимую единицу: Z=a+bi – от этого комплексное число не изменится. Но стандартно комплексное число принято записывать именно в таком порядке:
Z=a+bi
Чтобы всё было понятнее, сразу приведу геометрическую интерпретацию. Комплексные числа изображаются на комплексной плоскости:
Основные определения. Операции над комплексными числами
1. Существует элемент i (мнимая единица) такой, что i2 = – 1.
2. Символ a + bi называют комплексным числом с действительной частью a и мнимой частью bi, где a и b – действительные числа, b – коэффициент мнимой части.
Комплексное число a + 0i отождествляется с действительным числом a, т.е. a + 0i = a, в частности, 0 + 0i = 0. Числа вида bi (b 0) называют чисто мнимыми.
Например, комплексное число 2 + 3i имеет действительную часть – действительное число 2 и мнимую часть 3i, действительное число 3 – коэффициент мнимой части.
Комплексное число 2 – 3i имеет действительную часть число 2, мнимую часть – 3i, число – 3 – коэффициент при мнимой части.
3. Правило равенства. Два комплексных числа равны тогда и только тогда, когда равны их действительные части и равны коэффициенты мнимых частей.
Т.е., если a + bi = c +di, то a = c, b = d: и, обратно, если a = c, b = d, то a + bi = c +di.
единицу по действительной оси;
мнимую единицу ![]() по мнимой оси.
по мнимой оси.
Не нужно проставлять все значения: …–3, –2, –1, 0, 1, 2, 3,… и ![]() .
.

Рассмотрим чисел десять и
построим на комплексной плоскости следующие комплексные числа:
![]() ,
, ![]() ,
, ![]()
![]() ,
, ![]() ,
, ![]()
![]() ,
, ![]() ,
, ![]() ,
, ![]()

Модуль комплексного числа
Длина вектора, изображающего комплексное число, называется модулем комплексного числа. Модуль любого комплексного числа, не равного нулю, есть положительное число. Модуль комплексного числа a + b·i обозначается |a + b·i|, а также буквой r. Из чертежа видно, что:

Модуль действительного числа, совпадает с его абсолютным значением. Сопряженные комплексныечисла a + b·i и a - b·i
имеют один и тотже модуль.
Угол φ между осью абсцисс и вектором OM, изображающим комплексное число a + b·i,называется аргументом комплексного числа a + b·i
Каждое не равное нулю комплексное число имеет бесчисленное множество аргументов, отлuчающихся друг от друга на целое число полных оборотов (т.е. на 360°·k, где k - любое целое число). Аргумент комплексного числа связан с его координатами следующими формулами:

Однако ни одна из этих формул в отдельности не позволяет найти аргумент. Для того чтобы найти аргумент комплексного числа, эти формулы надо использовать в совокупности, а также учитывать номер четверти, на координатной плоскости, в которой находится комплексное число.
Найти модуль и аргумент , если ДАНО
Решение 1) Найдем модуль комплексного числа

2) Найдем аргумент комплексного числа
Пример 2Найти модуль и аргумент, если ДАНО комплексное число ![]()
Решение 1) Найдем модуль комплексного числа
![]()
2) Найдем аргумент комплексного числа
Сложение комплексных чисел
Правило сложения и вычитания комплексных чисел.
(a + bi) + (c + di) = (a + c) + (b + d)i.
Например: (2 + 3i) + (5 + i) = (2 + 5) + (3 + 1)i = 7 + 4i;
(– 2 + 3i) + (1 – 8i) = (– 2 + 1) + (3 + (– 8))i = – 1 – 5i;
(– 2 + 3i) + (1 – 3i) = (– 2 + 1) + (3 + (– 3))i =
= – 1 + 0i = – 1.
Вычитание комплексных чисел определяется как операция, обратная сложению, и выполняется по формуле:
(a + bi) – (c + di) = (a – c) + (b – d)i.
Например:
(5 – 8i) – (2 + 3i) = (3 – 2) + (– 8 – 3)i = 1 – 11i;
(3 – 2i) – (1 – 2i) = (3 – 1) + ((– 2) – (– 2))i = 2 + 0i = 2.
Пример 1
Сложить два комплексных числа ![]() ,
, ![]()
Для того чтобы сложить два комплексных числа нужно сложить их действительные и мнимые части:
![]()
Просто, не правда ли? Действие настолько очевидно, что не нуждается в дополнительных комментариях.
Таким нехитрым способом можно найти сумму любого количества слагаемых: просуммировать действительные части и просуммировать мнимые части.
Для комплексных чисел справедливо правило первого класса:
![]() – от перестановки слагаемых сумма не меняется.
– от перестановки слагаемых сумма не меняется.
Вычитание комплексных чисел
Пример 2
Найти разности комплексных чисел ![]() и
и ![]() , если
, если
![]() ,
, ![]()
Действие аналогично сложению, единственная особенность состоит в том, что вычитаемое нужно взять в скобки, а затем – стандартно раскрыть эти скобки со сменой знака:
![]()
Результат не должен смущать, у полученного числа две, а не три части. Просто действительная часть – составная: ![]() . Для наглядности ответ можно переписать так:
. Для наглядности ответ можно переписать так: ![]() .
.
Рассчитаем вторую разность:
![]()
Здесь действительная часть тоже составная: ![]()
Чтобы не было какой-то недосказанности, приведу короткий пример с «нехорошей» мнимой частью: ![]() .
.
Вот здесь без скобок уже не обойтись.
Умножение комплексных чисел
Настал момент познакомить вас со знаменитым равенством:
![]()
Пример 3
Найти произведение комплексных чисел ![]() ,
, ![]()
Очевидно, что произведение следует записать так:
![]()
Что напрашивается? Напрашивается раскрыть скобки по правилу умножения многочленов. Так и нужно сделать! Все алгебраические действия вам знакомы, главное, помнить, что ![]() и быть внимательным.
и быть внимательным.
Повторим, школьное правило умножения многочленов: Чтобы умножить многочлен на многочлен нужно каждый член одного многочлена умножить на каждый член другого многочлена.
Я распишу подробно:
![]()
Надеюсь, всем было понятно, что ![]()
Внимание, и еще раз внимание, чаще всего ошибку допускают в знаках.
Как и сумма, произведение комплексных чисел перестановочно, то есть справедливо равенство: ![]() .
.
В учебной литературе и на просторах Сети легко найти специальную формулу для вычисления произведения комплексных чисел. Если хотите, пользуйтесь, но мне кажется, что подход с умножением многочленов универсальнее и понятнее. Формулу приводить не буду, считаю, что в данном случае – это забивание головы опилками.
Деление комплексных чисел
Пример 4 Даны комплексные числа 
Найти частное комплексных чисел:  .
.
Решение:
 , где
, где

 действительная часть комплексного числа
действительная часть комплексного числа
 мнимая часть комплексного числа и i2 = - 1
мнимая часть комплексного числа и i2 = - 1
Деление чисел осуществляется методом умножения знаменателя и числителя на сопряженное знаменателю выражение.
Вспоминаем формулу разности квадратов ![]()
и смотрим на наш знаменатель: (5 – 2i).
В знаменателе уже есть (a - b), поэтому сопряженным выражением в данном случае является (a + b), то есть : ( 5 + 2i.)
Согласно правилу, знаменатель нужно умножить на ( 5 + 2i.)
и, чтобы ничего не изменилось, домножить числитель на то же самое число : ( 5 + 2i.)

Далее в числителе нужно раскрыть скобки (перемножить два числа по правилу, рассмотренному в предыдущем пункте). А в знаменателе воспользоваться формулой ^ (a + b)(a - b) = a2 - b2 (помним, что и i2 = - 1)
Рассмотрим более подробно решение:

Пример, рассмотрим частное чисел:
Пример 5 Даны комплексные числа 
Найти частное комплексных чисел:  .
.
. Перед делением избавляемся от лишних минусов: в числителе и в знаменателе выносим минусы за скобки и сокращаем эти минусы
Найти частное комплексных чисел:  .
.
. Пример 6 Встречаются и такого вида задания:
Данное комплексное число можно преобразовать следующим образом :  .
.
Записать данное число в алгебраической форме (т.е. в форме (a+bi)).
Приём тот же самый – умножаем знаменатель и числитель на сопряженное знаменателю выражение. Снова смотрим на формулу ![]() . В знаменателе уже есть (a - b), поэтому знаменатель и числитель нужно домножить на сопряженное выражение (a + b), то есть на
. В знаменателе уже есть (a - b), поэтому знаменатель и числитель нужно домножить на сопряженное выражение (a + b), то есть на  :
:

Пример 6
Даны два комплексных числа ,  . Решите самостоятельно с последующей проверкой:
. Решите самостоятельно с последующей проверкой:
Найдите их сумму, разность, произведение и частное.
Проверка решения: Сумма Z1 + Z2/ =(8 - 3i) + (8 + 3i) = 16
Разность двух комплексных чисел: Z1 - Z2/ = (8-3i) - (8 + 3i) = - 6 i
Z1 * Z2/ =(8-3i) * (8 + 3i) = 64 - 24 i +24 i - 9 i 2 = 64 +9 = 73 или
Z1 * Z2/ =(8-3i) * (8 + 3i) = 64 - 9 i 2 = 64 +9 = 73 (формула разности квадратов)

Извлечение корней из комплексных чисел.
Решение квадратных уравнений с отрицательным дискриминантом
Принято считать 
I. Решть уравнение: 1) х2 + 9 = 0; 2) х2 + 16 = 0; 3) х2 + 25 = 0
Решение: 1) х2 + 9 = 0
Действительно ли найденные корни являются решением уравнения х2 + 9 = 0? Выполним проверку:
(3i)2 = 9i2 = - 9 Действительно, х2 + 9 = 0;
(- 3i)2 = 9i2 = - 9 тогда действительно, х2 + 9 = 0;
Что и требовалось проверить.
2) х2 + 16 = 0
3) х2 + 25 = 0
II Решть уравнение: 1) х2 + 8x + 20 = 0; 2) х2 - 16x + 100 = 0; 3) х2 - 10x+ 50 = 0
Решение:
1) х2 + 8x + 20 = 0 
Ответ: X1 = - 4 + 2i ; X 2 = - 4 - 2i
2) х2 - 16x + 100 = 0; 
Ответ: X1 = 8 + 6i ; X 2 = 8 - 6i
3) х2 - 10x+ 50 = 0
Ответ: X1 = 5 + 5i ; X 2 = 5 - 5i
Часто используется сокращенная запись, оба корня записывают в одну строчку:  .
.
Такие корни также называют сопряженными комплексными корнями.
Как извлекать квадратные корни из отрицательных чисел, думаю, всем понятно: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() и т.д. Во всех случаях получается два сопряженных комплексных корня.
и т.д. Во всех случаях получается два сопряженных комплексных корня.
Пример 4
Решить квадратное уравнение ![]()
Вычислим дискриминант:
![]()
Дискриминант отрицателен, и в действительных числах уравнение решения не имеет. Но корень можно извлечь в комплексных числах!
![]()
По известным формулам получаем два корня:
![]()
![]() – сопряженные комплексные корни
– сопряженные комплексные корни
Таким образом, уравнение ![]() имеет два сопряженных комплексных корня:
имеет два сопряженных комплексных корня: ![]() ,
, ![]()
Нетрудно понять,что в поле комплексных чисел «школьное» квадратное уравнение всегда при двух корнях! И вообще, любое уравнение вида имеет ровно n корней, часть из которых могут быть комплексными.
Простой пример для самостоятельного решения:
Пример 5
Найти корни уравнения 9х4 - 1 = 0 и разложить квадратный двучлен на множители.
Разложение на множители осуществляется опять же по школьной формуле.
На чистовик так подробно оформлять, конечно, не нужно, это сделано мной для того, чтобы вам было понятно, откуда что взялось.
Очень часто полученные корни требуется изобразить геометрически:
Самостоятельно решить уравнения: Найдите их сумму, разность, произведение и частное.
1) Z1 =5 + 9i u Z2 = 5 - 9i.
2) Z1 = 3 + 6i u Z2 = 3 - 6i.
3) Z1 = - 4 + 5i u Z2 = 5 - 9i\
Решения и ответы:
Пример 1:
Решение:
1) Z1 = 5 + 9i u Z2 = 5 - 9i Z1 + Z2 =( 5+ 9i ) + (5 - 9i) = 10
Z1 = 5 + 9i u Z2 = 5 - 9i Z1 - Z2 =( 5+ 9i ) - (5 - 9i) = 18 i
Z1 * Z2 =( 5+ 9i ) * (5 - 9i) = 25 - 81 i2= 25 + 81 = 106

Задание для самостоятельной работы.
Вариант 1.
1 ) (4 -3i)+(-2 + i); 2) (0,4 – 0,3i)+(-0,9 + 1,7 i); 3) (-0,4 -2i) + (0,6 +5i);
4) (0,4 – 0,3i)-(-0,9 + 1,7 i); 5) (4 -3i)+(-2 + i); 6) (4 -3i)*(-2 + i);
7) (-0,4 -2i)*(0,6 +5i); 8) (-0,4 -2i)*(0,6 +5i);
9) 
Вариант 2.
1 ) (14 -3i)+(-12 + 5i); 2) (0,4 – 0,3i)-(-0,9 + 1,7 i); 3) (-0,4 -2i)*(0,6 +5 i);
4) (0,5 – 0,3i)*(-9 + 1,7 i); 5) (4 -3i):(-2 + i); 6) (7 -2i)*(-7 + i);
7) (-0,4 -2i)*(0,6 +5 i); 8) (-0,4 -2i)+(0,6 +5 i)=0;
9) 
3.Содержание отчёта.
3.1 Название работы.
3.2 Выполнение работы.
Практическое занятие № 2 .
Действия над матрицами.
Цель: Выработать навыки действий над матрицами.
Требования к умениям и навыкам.
Должен знать: Определение матрицы, равенство матриц, сложение матриц, умножение матрицы на число, умножение матриц.
Должен уметь: Применять теоретические знания к решению практических задач.
3.Задание:
1. Изучить теоретический материал;
2. Рассмотреть примеры с решениями, записать их в тетрадь;
3. Выполнить самостоятельную работу по вариантам.
4. Сделать отчёт.
Методические указания.
Краткий теоретический материал.
Матрицей размера n×m называется прямоугольная таблица специального вида, состоящая из n строк и m столбцов, заполненная числами.
Количество строк и столбцов задают размеры матрицы.
Элементы матрицы
Элементы матрицы A обозначаются aij, где i - номер строки, в которой находится элемент, j - номер столбца.
Единичной матрицей называется такая квадратная матрица, диагональные элементы которой равны единицам, а остальные равны нулю

Равенство матриц. Две матрицы A и B называются равными, если они имеют одинаковое число строк и столбцов и их соответствующие элементы равны aij = bij. Так если  и
и  , то A=B, если a11 = b11, a12 = b12, a21 = b21 и a22 = b22
, то A=B, если a11 = b11, a12 = b12, a21 = b21 и a22 = b22
Сложение матриц. Пусть матрицы A и B состоят из одинакового числа строк и одинакового числа столбцов, т.е. имеют одинаковые размеры. Тогда для того, чтобы сложить матрицы A и B нужно к элементам матрицы A прибавить элементы матрицы B, стоящие на тех же местах. Таким образом, суммой двух матриц A и B называется матрица C, которая определяется по правилу, например,

или
![]()
Умножение матрицы на число. Для того чтобы умножить матрицу A на число k нужно каждый элемент матрицы A умножить на это число. Таким образом, произведение матрицы A на число k есть новая матрица, которая определяется по правилу  или
или ![]() .
.
Для любых чисел a и b и матриц A и B выполняются равенства:
![]()
![]()
![]()
Умножение матриц. Эта операция осуществляется по своеобразному закону. Прежде всего, заметим, что размеры матриц–сомножителей должны быть согласованы. Перемножать можно только те матрицы, у которых число столбцов первой матрицы совпадает с числом строк второй матрицы (т.е. длина строки первой равна высоте столбца второй). Произведением матрицы A не матрицу B называется новая матрица C=AB, элементы которой составляются следующим образом:
 .
.
Таким образом, например, чтобы получить у произведения (т.е. в матрице C) элемент, стоящий в 1-ой строке и 3-м столбце c13, нужно в 1-ой матрице взять 1-ую строку, во 2-ой – 3-й столбец, и затем элементы строки умножить на соответствующие элементы столбца и полученные произведения сложить. И другие элементы матрицы-произведения получаются с помощью аналогичного произведения строк первой матрицы на столбцы второй матрицы.
В общем случае, если мы умножаем матрицу A = (aij) размера m×n на матрицу B = (bij) размера n×p, то получим матрицу C размера m×p, элементы которой вычисляются следующим образом: элемент cij получается в результате произведения элементов i-ой строки матрицы A на соответствующие элементы j-го столбца матрицы B и их сложения.
Из этого правила следует, что всегда можно перемножать две квадратные матрицы одного порядка, в результате получим квадратную матрицу того же порядка. В частности, квадратную матрицу всегда можно умножить саму на себя, т.е. возвести в квадрат.
Другим важным случаем является умножение матрицы–строки на матрицу–столбец, причём ширина первой должна быть равна высоте второй, в результате получим матрицу первого порядка (т.е. один элемент). Действительно,

Квадратная матрица - это матрица с равным числом столбцов и строк.
Главная диагональ квадратной матрицы — диагональ, которая проходит через верхний левый и нижний правый углы.
Побочной диагональю матрицы называется диагональ, идущая из левого нижнего угла в правый верхний угол.
Треугольная матрица — квадратная матрица, в которой все элементы ниже или выше главной диагонали равны нулю.
Диагональная матрица — квадратная матрица, все элементы которой вне главной диагонали равны нулю.
1. Найти матрицу, противоположную матрице А =  .
.
Решение. Для нахождения противоположной матрицы умножаем матрицу А на к = -1: - А =  .
.
2. Найти линейную комбинацию 3А - 2В, если
А =  , В =
, В =  .
.
Решение. Сначала находим произведение А на к1 = 3 и В на к2 = -2:
3А =  , - 2В =
, - 2В =  .
.
Теперь найдем сумму полученных матриц:
3А - 2В =  =
=  .
.
3. Найти произведение АВ, если А =  , В =
, В =  .
.
Решение. АВ =  =
=  .
.
Задание для самостоятельной работы.
Вариант 1:
Найти сумму матриц. а) ,
, 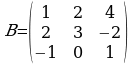 ,
,
б)  ,
,  .
.
Найти матрицу С = 2А + 5В, если  ,
,  .
.
Найти произведение матриц АВ и ВА, если: а)  ,
,  ,
,
б)  ,
,  .
.
Вариант 2.
Найти сумму матриц: а).  ,
,  ,
,
б)  ,
, 
Найти матрицу С = 4А + 3В, если  ,
,  .
.
Найти произведение матриц АВ и ВА, если: а)  ,
,  ,
,
б)  ,
, 
3. Содержание отчёта.
3.1 Название работы.
3.2 Выполнение работы.
Практическое занятие № 3.
Определители второго и третьего порядков.
Цель: Сформировать знания, умения и навыки по вычислению определителей второго и третьего порядка.
Требования к умениям и навыкам.
Должен знать: Определения, правило вычисления и свойства определителей второго и третьего порядков.
Должен уметь: Применять теоретические знания к решению практических задач.
3.Задание:
1. Изучить теоретический материал;
2. Рассмотреть примеры с решениями, записать их в тетрадь;
3. Выполнить самостоятельную работу по вариантам.
4. Сделать отчёт.
Методические указания.
Краткий теоретический материал.
Пусть дана матрица
.
Число  называется определителем второго порядка, соответствующим данной матрице, и обозначается символами
называется определителем второго порядка, соответствующим данной матрице, и обозначается символами  (det A,
(det A,  ):
):
 =
= =
= -
- .
.
Определитель матрицы A размера 2x2 (определитель 2-го порядка) – это число, которое можно найти по правилу: произведение элементов, стоящих на главной диагонали матрицы, минус произведение элементов, стоящих на побочной диагонали.
Определитель второго порядка содержит две строки и два столбца, числа  ,
,  ,
,  ,
,  – элементы определителя. Правило вычисления определителя второго порядка можно представить схематически:
– элементы определителя. Правило вычисления определителя второго порядка можно представить схематически:



 .
.
Количество строк и столбцов в определителе всегда совпадает. Кроме определителей второго порядка существуют определители 3-го, 4-го и т. д. порядков. Определитель 3-го порядка содержит три строки и три столбца:
 .
.
Для вычисления определителя 3-го порядка существует несколько правил.
ВЫЧИСЛЕНИЕ ОПРЕДЕЛИТЕЛЕЙ ТРЕТЬЕГО ПОРЯДКА
1.ПРАВИЛО ПРЯМОУГОЛЬНИКА
Для вычисления определителя надо повторить запись первого и второго столбцов. Проведем три левые диагонали, начиная с верхнего левого угла, и три правые диагонали. Три первые слагаемые получаются как результат произведения элементов, стоящих на каждой из левых диагоналей. Следующие три слагаемые получаются при умножении элементов, стоящих на каждой из правых диагоналей. Три последние произведения берутся с противоположным знаком.
Пример 1.







 .
.
2
 . ПРАВИЛО ТРЕУГОЛЬНИКА
. ПРАВИЛО ТРЕУГОЛЬНИКА


(1) (2)
Перемножаются элементы, стоящие на левых диагоналях. Одна диагональ, главная, проходит через три элемента, и две диагонали побочные проходят через два элемента, третьим элементом для них является элемент, стоящий в вершине треугольника (схема 1). Аналогично находим произведения элементов, стоящих на правых диагоналях (схема 2). Эти произведения берутся с обратным знаком.
 .
.
Пример 2.

 .
.
Задание для самостоятельной работы.
Вариант 1:
Вычислить определители 2-го порядка: а)  б)
б) 
Вычислить определители 3-го порядка двумя способами: а)  б)
б) 
Вариант 2:
Вычислить определители 2-го порядка: а) )  б)
б) 
Вычислить определители 3-го порядка двумя способами: а)  б)
б) 
3. Содержание отчёта.
3.1 Название работы.
3.2 Выполнение работы.
Практическое занятие № 4.
Формулы Крамера (для систем линейных уравнений с тремя неизвестными).
Цель: Сформировать знания, умения и навыки по решению систем уравнений с помощью формул Крамера.
Требования к умениям и навыкам.
Должен знать: Определения, правило вычисления и свойства определителей второго и третьего порядков. Формулы Крамера решения систем уравнений.
Должен уметь: Применять теоретические знания к решению практических задач.
3.Задание:
1. Изучить теоретический материал;
2. Рассмотреть примеры с решениями, записать их в тетрадь;
3. Выполнить самостоятельную работу по вариантам.
4. Сделать отчёт.
Методические указания.
Краткий теоретический материал.
Определители второго и третьего порядка.
Определение 1. Определителем второго порядка, составленного из чисел  , называется число, определяемое равенством
, называется число, определяемое равенством  .
.
Числа  , называются элементами определителя.
, называются элементами определителя.
При этом из произведения элементов, стоящих на так называемой главной диагонали матрицы (идущей из левого верхнего в правый нижний угол) вычитается произведение элементов, находящихся на второй, или побочной, диагонали.
 Схема расчета определителя матрицы 2×2.
Схема расчета определителя матрицы 2×2.
Примеры.
1. 2.
2.  .
.
Определение 2. Определителем третьего порядка называется число, определяемое с помощью элементов квадратной матрицы третьего порядка следующим образом:

Замечание. Для того, чтобы легче запомнить эту формулу, можно использовать так называемое правило треугольников. Оно заключается в следующем: элементы, произведения которых входят со знаком «+», располагаются так:






 , образуя два треугольника, симметричных относительно главной диагонали.
, образуя два треугольника, симметричных относительно главной диагонали.
Э





 лементы, произведения которых входят в определитель со знаком
лементы, произведения которых входят в определитель со знаком  , располагаются аналогичным образом относительно побочной диагонали:
, располагаются аналогичным образом относительно побочной диагонали:  .
.
Схема вычисления определителя третьего порядна

Первые два столбца матрицы записываются справа возле матрицы. Произведения элементов, стоящих на линях со знаком «плюс», складываются, затем вычитаются произведения элементов, находящихся на линях со знаком «минус»
Примеры:
1.
2. 
Формулы Крамера решения систем двух уравнений с двумя неизвестными.
Рассмотрим систему двух линейных уравнений с двумя неизвестными в общем виде:

 следующим образом: чтобы исключить
следующим образом: чтобы исключить  умножим первое уравнение на
умножим первое уравнение на  и из полученного уравнения вычтем второе, умноженное на
и из полученного уравнения вычтем второе, умноженное на  :
: 

 . Для определения
. Для определения  поступим так: умножим второе уравнение на
поступим так: умножим второе уравнение на  и из полученного уравнения вычтем первое, умноженное на
и из полученного уравнения вычтем первое, умноженное на  :
:


 . Из (1) и (2) видно, что если
. Из (1) и (2) видно, что если  , то система имеет единственное
, то система имеет единственное  , определяемое формулой
, определяемое формулой 
Если  , система имеет единственное решение, определяемое по формуле:
, система имеет единственное решение, определяемое по формуле: .
.
Если  , система имеет бесконечно много решений.
, система имеет бесконечно много решений.
Если  , а хотя бы один из
, а хотя бы один из  , система не имеет решений.
, система не имеет решений.
1 Если говорить строго, то из (1) и (2) следует, что если решение существует, то оно единственным образом выражается через коэффициенты системы и свободные члены. Чтобы доказать существование, надо подставить две формулы (3) в систему и убедиться в том, что оба уравнения обращаются в верные равенства.
Примеры: Решить систему уравнений с помощью формул Крамера.

Решение: 1. Составим определители 
 .
.
Так как  , система имеет единственное решение, определяемое по формулам:
, система имеет единственное решение, определяемое по формулам: 
 . Таким образом, пара чисел (21; 13) – решение системы. Ответ: (21; 13)
. Таким образом, пара чисел (21; 13) – решение системы. Ответ: (21; 13)
Решение: 2. Рассмотрим систему  и применим к ней правило Крамера. Найдём все нужные определители:
и применим к ней правило Крамера. Найдём все нужные определители:
 , следовательно, система имеет единственное решение.
, следовательно, система имеет единственное решение.
 .
.
 . Ответ:
. Ответ:  .
.
Решение: 3.  . Здесь
. Здесь 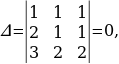 поскольку имеет два одинаковых столбца. Следовательно, система не имеет единственного решения. Найдём
поскольку имеет два одинаковых столбца. Следовательно, система не имеет единственного решения. Найдём  ,
,  и
и  :
:
 ,
,  ,
,  , поэтому система имеет бесконечно много решений.
, поэтому система имеет бесконечно много решений.
 4.
4.  . Для этой системы
. Для этой системы  но
но  , следовательно, решений нет.
, следовательно, решений нет.
Задание для самостоятельной работы.
Вариант 1:
Решите систему уравнений по формулам Крамера:
1)  , 2)
, 2) , 3)
, 3)  4)
4) 
Вариант 2.
Решите систему уравнений по формулам Крамера:
 . 2)
. 2)  , 3)
, 3)  4)
4) 
3. Содержание отчёта.
3.1 Название работы.
3.2 Выполнение работы.
Практическое занятие № 6.
Решение матричных уравнений.
Цель: применить знания, умения и навыки при решении уравнений.
Требования к умениям и навыкам.
Должен знать: правила вычисления обратной матрицы.
Должен уметь: находить алгебраические дополнения, вычислять определитель, решать матричные уравнения.
Задание:
1. Изучить теоретический материал;
2. Рассмотреть примеры с решениями, записать их в тетрадь;
3. Выполнить самостоятельную работу по вариантам;
4. Сделать отчёт.
Теоретические сведения и методические рекомендации
по решению задач.
Обратная матрица.
Определим операцию деления матриц как операцию, обратную умножению.
Определение. Если существуют квадратные матрицы Х и А, удовлетворяющие условию:
XA = AX = E,
где Е - единичная матрица того же самого порядка, то матрица Х называется обратной к матрице А и обозначается А-1.
Каждая квадратная матрица с определителем, не равным нулю имеет обратную матрицу и притом только одну.
Рассмотрим общий подход к нахождению обратной матрицы.
Исходя из определения произведения матриц, можно записать:
AX = E , i=(1,n), j=(1,n),
eij = 0, i j,
eij = 1, i = j .
Таким образом, получаем систему уравнений:
Решив эту систему, находим элементы матрицы Х.
Пример 1. Дана матрица А = , найти А-1.
Таким образом, А-1=.
Однако, такой способ не удобен при нахождении обратных матриц больших порядков, поэтому обычно применяют следующую формулу:
,
где Мji- дополнительный минор элемента аji матрицы А.
Пример 2. Дана матрица А = , найти А-1.
det A = 4 - 6 = -2.
M11=4; M12= 3; M21= 2; M22=1
x11= -2; x12= 1; x21= 3/2; x22= -1/2
Таким образом, А-1=.
Cвойства обратных матриц.
Укажем следующие свойства обратных матриц:
(A-1)-1 = A;
2) (AB)-1 = B-1A-1
(AT)-1 = (A-1)T.
Вариант 1.
1. Решить уравнение:
а)![]() б)
б)![]()
2. Вычислить определитель:
а) б)
б)
3. Найти rang A
А=
4.Найти обратную матрицу:
А=
5. Решить матричное уравнение:
![]()
6.Найти : Х=?
![]()
Вариант 2.
1.Решить уравнение:
а)![]() б)
б)![]()
2.Вычислить определитель:
а) б)
б)
3.Найти rang A
А=
4.Найти А-1=?,если
А=
5.Решить матричное уравнение:
![]()
6.Найти Х=?
![]()
3. Содержание отчёта.
3.1 Название работы.
3.2 Выполнение работы.
Практическое занятие № 7.
Графический метод решения задачи линейного программирования.
Цель: решение задачи линейного программирования графическим методом.
Требования к умениям и навыкам.
Должен знать: основные понятия, формулы и правила линейного программирования
Должен уметь: применять основные формулы и правила линейного программирования.
Теоретические сведения
Наиболее простым и наглядным методом линейного программирования (ЛП) является графический метод. Он применяется для решения задач ЛП с двумя переменными.
Рассмотрим задачу ЛП в стандартной форме записи:

Положим n=2 , т.е. рассмотрим эту задачу на плоскости. Пусть система неравенств совместна (имеет хотя бы одно решение).
Каждое неравенство этой системы геометрически определяет полуплоскость с граничной прямой ai1 x1 + ai2 x2 = b i , i=1,2,… m . Условия неотрицательности определяют полуплоскости, соответственно, с граничными прямыми x1=0, x2 =0. Система совместна, поэтому полуплоскости, как выпуклые множества, пересекаясь, образуют общую часть, которая является выпуклым множеством и представляет собой совокупность точек, координаты каждой из которых являются решением данной системы. Совокупность этих точек называют многоугольником решений. Он может быть точкой, отрезком, лучом, многоугольником, неограниченной многоугольной областью.
Таким образом, геометрически задача линейного программирования (ЗЛП) представляет собой отыскание такой точки многоугольника решений, координаты которой доставляют линейной функции цели максимальное (минимальное) значение, причем допустимыми решениями являются все точки многоугольника решений.
Линейное уравнение описывает множество точек, лежащих на одной прямой. Линейное неравенство описывает некоторую область на плоскости. Определим, какую часть плоскости описывает неравенство 2х1 +3х2 £ 12. Во-первых, построим прямую 2х1 +3х2 =12 . Эта прямая проходит через точки (6, 0) и (0, 4). Для того чтобы определить, какая полуплоскость удовлетворяет неравенству необходимо выбрать любую точку на графике, не принадлежащую прямой, и подставить ее координаты в неравенство. Если неравенство будет выполняться, то данная точка является допустимым решением и полуплоскость, содержащая точку, удовлетворяет неравенству. Удобной для использования при подстановке в неравенство является начало координат. Подставим х1 =х2 =0 в неравенство 2х1 +3х2 £ 12 . Получим 2´0+3´0£12. Данное утверждение является верным, следовательно, неравенству 2х1 +3х2 £12 соответствует нижняя полуплоскость, содержащая точку (0.0). Это отражено на графике, изображенном на. 1.
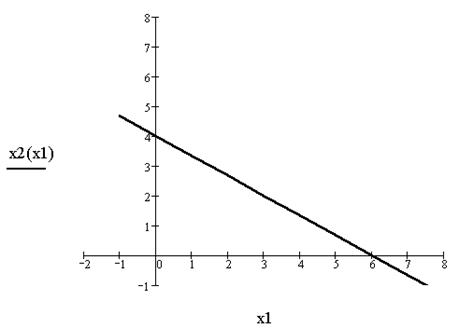
Рис. 1. Неравенству 2х1 +3х2 £12 соответствует нижняя полуплоскость.
Аналогично можно изобразить графически каждое ограничение задачи линейного программирования.
Решением каждого неравенства системы ограничений ЗЛП является полуплоскость, содержащая граничную прямую и расположенная по одну сторону от нее. Пересечение полуплоскостей, каждая из которых определяется соответствующим неравенством системы, называется областью допустимых решений или областью определения. Необходимо помнить, что область допустимых решений удовлетворяет условиям неотрицательности (xj ³0, j=1,…, n). Координаты любой точки, принадлежащей области определения являются допустимым решением задачи.
Для нахождения экстремального значения целевой функции при графическом решении задач ЛП используют вектор–градиент, координаты которого являются частными производными целевой функции, т.е.
![]()
Этот вектор показывает направление наискорейшего изменения целевой функции. Прямая ![]() , состоит в том, что при параллельном смещении линии в одну сторону уровень перпендикулярная вектору–градиенту, является линией уровня целевой функции. В любой точке линии уровня целевая функция принимает одно и то же значение. Приравняем целевую функцию постоянной величине «a». Меняя значение «a» , получим семейство параллельных прямых, каждая из которых является линией уровня.
, состоит в том, что при параллельном смещении линии в одну сторону уровень перпендикулярная вектору–градиенту, является линией уровня целевой функции. В любой точке линии уровня целевая функция принимает одно и то же значение. Приравняем целевую функцию постоянной величине «a». Меняя значение «a» , получим семейство параллельных прямых, каждая из которых является линией уровня.
Важное свойство линии уровня линейной функции только возрастает, а при смещении в другую сторону – убывает.
С геометрической точки зрения в задаче линейного программирования ищется такая угловая точка или набор точек из допустимого множества решений, на котором достигается самая верхняя (нижняя) линия уровня, расположенная дальше (ближе) остальных в направлении наискорейшего роста.
Графический метод решения ЗЛП состоит из следующих этапов:
1. Строится многоугольная область допустимых решений ЗЛП – ОДР,
2. Строится вектор-градиент ЦФ в какой-нибудь точке Х0 принадлежащей ОДР –
![]() .
.
3. Линия уровня C1 x1 +C2 x2 = а (а –постоянная величина) – прямая, перпендикулярная вектору – градиенту ![]() – передвигается в направлении этого вектора в случае максимизации f(x1, x2 ) до тех пор, пока не покинет пределов ОДР. Предельная точка (или точки) области при этом движении и является точкой максимума f(x1, x2 ).
– передвигается в направлении этого вектора в случае максимизации f(x1, x2 ) до тех пор, пока не покинет пределов ОДР. Предельная точка (или точки) области при этом движении и является точкой максимума f(x1, x2 ).
4. Для нахождения ее координат достаточно решить два уравнения прямых, получаемых из соответствующих ограничений и дающих в пересечении точку максимума. Значение f(x1, x2 ), найденное в получаемой точке, является максимальным.
При минимизации f(x1, x2 ) линия уровня перемещается в направлении, противоположном вектору-градиенту. Если прямая при своем движении не покидает ОДР, то соответствующий максимум или минимум f(x1, x2 ) не существует.
Если линия уровня параллельна какому-либо функциональному ограничению задачи, то оптимальное значение ЦФ будет достигаться в любой точке этого ограничения, лежащей между двумя оптимальными угловыми точками, и, соответственно, любая из этих точек является оптимальным решением ЗЛП.
.
Задания для самостоятельной работы
1. Дана математическая модель задачи ЛП: 𝐹 = 2𝑘𝑥1 + 𝑘 𝑥2 → min;
−2𝑥1 + 3 𝑥2 ≤ 6,
𝑥1 − 𝑘 𝑥2 ≥ 1,
𝑘 𝑥1 + 𝑥2 ≥ 5,
𝑥1 ≥ 0, 𝑥2 ≥ 0
Здесь 𝑘 = 1 + 𝑁
𝑛+1 ;
𝑁 − последняя цифра номера группы, в которой учится студент.
𝑛 − порядковый номер студента в списке группы.
Найти решение задачи графическим методом.
2. Ответьте на вопросы:
1. Сформулируйте общую задачу линейного программирования.
2. Напишите в различных формах (векторной, матричной, с помощью
сумм) математическую модель общей задачи линейного программирования.
3. Дайте определение плана, невырожденного и вырожденного опорного плана, оптимального плана.
4. Какое множество называется выпуклым? Приведите примеры выпуклых множеств.
5. Какая точка выпуклого множества называется угловой?
6. Какими свойствами обладает выпуклое множество?
7. Что называется многогранником решений?
8. Дайте геометрическое истолкование задачи линейного программирования.
9. В какой точке многогранника решений линейная функция задачи линейного программирования достигает своего оптимального значения?
10. Какой вид имеет угловая точка многогранника решений и какому
плану она соответствует?
11. Какие планы необходимо исследовать, чтобы найти оптимальное
значение линейной функции?
Задание:
1. Изучить теоретический материал;
2. Рассмотреть примеры с решениями, записать их в тетрадь;
3. Выполнить самостоятельную работу по вариантам;
4. Сделать отчёт.
Методические указания.
Краткие теоретические сведения.
Предел последовательности
1.Определение. Число ![]() называется пределом последовательности
называется пределом последовательности ![]() , если для любого положительного
, если для любого положительного ![]() числа найдется такое натуральное число
числа найдется такое натуральное число ![]() , что при всех
, что при всех ![]()
![]() выполняется неравенство
выполняется неравенство ![]()
Пишут: ![]()
![]()
Графически это выглядит так:
![]() n -
n - ![]()
![]()
 Т.е. элемент
Т.е. элемент ![]() находится в
находится в ![]() - окрестности точки а. При этом последовательности
- окрестности точки а. При этом последовательности ![]() называется сходящейся, в противном случае – расходящейся.
называется сходящейся, в противном случае – расходящейся.
Основные свойства сходящихся последовательностей
1)Сходящаяся последовательность ограничена.
2)Пусть ![]() ,
, ![]() , тогда а)
, тогда а) ![]() б)
б) ![]() в)
в) ![]()
3)Если ![]() и для всех
и для всех ![]() выполняется неравенства
выполняется неравенства ![]() , то
, то ![]() .
. ![]()
4) Если ![]() и последовательность {уn} - ограниченная, то
и последовательность {уn} - ограниченная, то ![]()
2. Определение. Пусть функция  определена в некоторой окрестности точки
определена в некоторой окрестности точки  , кроме, быть может, самой точки
, кроме, быть может, самой точки  . Число B называется пределом функции
. Число B называется пределом функции  в точке
в точке  , или при
, или при  стремящемся к
стремящемся к  , если для любой последовательности
, если для любой последовательности  стремящемся к
стремящемся к  , последовательность соответствующих значений функции
, последовательность соответствующих значений функции  сходится к числу B. В этом случае пишут
сходится к числу B. В этом случае пишут  .
.
3. Понятие бесконечно малой и бесконечно большой величины.
Если предел функции равен нулю  , то она называется бесконечно малой величиной. Следовательно, выполняется равенство
, то она называется бесконечно малой величиной. Следовательно, выполняется равенство  .
.
Если предел функции равен бесконечности  , т.е. величине, обратной бесконечно малой величине, то она называется бесконечно большой величиной. Выполняется равенство:
, т.е. величине, обратной бесконечно малой величине, то она называется бесконечно большой величиной. Выполняется равенство:  .
.
4. Теоремы о пределах.
Теорема 1. Предел суммы (разности) двух функций равен сумме (разности) их пределов:
![]()
Теорема справедлива для алгебраической суммы любого конечного числа функций.
Теорема 2. Функция может иметь только один предел при ![]() .
.
![]()
![]()
Теорема 3. Предел произведения двух функций равен произведению их пределов:
![]() .
.
Следствие 1. Постоянный множитель можно выносить за знак предела: ![]()
Следствие 2. Предел степени с натуральным показателем равен той же степени предела: ![]() .
.
Теорема 4. Предел дроби равен пределу числителя, деленному на предел знаменателя, если предел знаменателя не равен нулю.
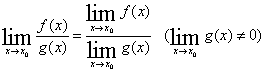
3. Методы нахождения пределов функции:
1.Простая подстановка значения аргумента.
Пример 1. 
Пример 2. 
Пример 3.  .
.
Если при простой подстановке получаются неопределённости типа  или
или  , то используются способы 2 и 3.
, то используются способы 2 и 3.
2. Числитель и знаменатель делятся на x с наибольшим показателем степени.
Пример 4.  .
.
3. Дробь раскладывается на множители, согласно правилам сокращённого умножения.
1. 
4.  .
.
Пример 5. 
или разложения квадратного трёхчлена на множители
 где
где  и
и  корни квадратного трёхчлена.
корни квадратного трёхчлена.
Пример 6. 
4. Иррациональные функции. Если неопределённое выражение содержит иррациональность, то умножая на сопряженное выражение числитель и знаменатель, переводят иррациональность из знаменатель в числитель или наоборот.
Пример 7.  .
.
5.Первый замечательный предел.  используется при раскрытии неопределённостей вида
используется при раскрытии неопределённостей вида  в тригонометрических выражениях.
в тригонометрических выражениях.
Пример 8. 
Пример 9. 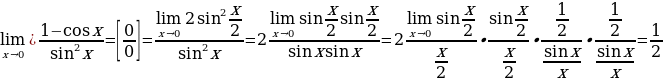
6.Второй замечательный предел. 
Используют при вычислении пределов вида  , где
, где 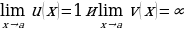 (что даёт неопределённость вида
(что даёт неопределённость вида  ).
).
Пример 10.  .
.
Задание для самостоятельной работы.
Вариант 1.
1. Найти предел последовательности: 
2.Вычислить пределы: 1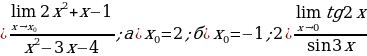 .
.
3.Найти предел функции на бесконечности: 
Вариант 2.
1. Найти предел последовательности: 
2.Вычислить пределы: 1 .
.
3.Найти предел функции на бесконечности: 
3. Содержание отчёта.
3.1. Название работы.
3.2. Выполнение работы.
Практическое занятие № 6.
Точки разрыва.
Цель: Отработка навыков исследования функции на непрерывность, нахождения точек разрыва и их классификации.
Требования к умениям и навыкам.
Должен знать: Определение непрерывной функции в точке и на промежутке, классификацию точек разрыва, свойства непрерывной функции.
Должен уметь: Применять методы нахождения пределов. Применять теоретические знания к решению практических задач.
Задание:
1. Изучить теоретический материал;
2. Рассмотреть примеры с решениями, записать их в тетрадь;
3. Выполнить самостоятельную работу по вариантам;
4. Сделать отчёт.
Методические указания.
Краткие теоретические сведения.
Понятие непрерывности функции в точке и на промежутке.
Определение 1. Функция  называется непрерывной в точке
называется непрерывной в точке  , если предел функции при
, если предел функции при  равен значению функции при
равен значению функции при  , т.е.
, т.е.  .
.
Обозначая  (приращение аргумента) и
(приращение аргумента) и  (приращение функции), условие непрерывности можно сформулировать так: функция непрерывна в точке
(приращение функции), условие непрерывности можно сформулировать так: функция непрерывна в точке  тогда и только тогда, когда в этой точке бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции.
тогда и только тогда, когда в этой точке бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции.
Если функция непрерывна в каждой точке множества, то она называется непрерывной на этом множестве.
Функция непрерывна на промежутке, если она непрерывна в каждой точке этого промежутка.
Все основные элементарные функции – постоянная, показательная, логарифмическая, степенная, тригонометрическая, обратные тригонометрические непрерывные на своих областях определения.
Функция  непрерывна на интервале
непрерывна на интервале  , если она непрерывна в каждой точке этого интервала.
, если она непрерывна в каждой точке этого интервала.
Теорема. Пусть функции  непрерывны в точке
непрерывны в точке  . Тогда функции
. Тогда функции 
 будут также непрерывны в точке
будут также непрерывны в точке  (для дроби при условии, что
(для дроби при условии, что  .
.
Классификация точек разрыва.
Ели нарушается одно из условий, то  называется точкой разрыва функции. Точки разрыва функции – это точки, в которых функция не является непрерывной.
называется точкой разрыва функции. Точки разрыва функции – это точки, в которых функция не является непрерывной.
Пусть  предел слева для функции
предел слева для функции  ,
,  предел справа,
предел справа,
 значение функции в точке
значение функции в точке  . Точки разрыва, в которых функция не является непрерывной, классифицируются следующим образом.
. Точки разрыва, в которых функция не является непрерывной, классифицируются следующим образом.
Устранимый разрыв. Точка  называется точкой устранимого разрыва функции
называется точкой устранимого разрыва функции  , если предел функции в этой точке существует, но в точке
, если предел функции в этой точке существует, но в точке  функция
функция  не определена, либо её значение в этой точке
не определена, либо её значение в этой точке  не равно пределу в этой точке, т.е.
не равно пределу в этой точке, т.е.  .
.
Разрыв первого рода (скачок).
Точка  называется точкой разрыва первого рода функции
называется точкой разрыва первого рода функции  , если в этой точке функция
, если в этой точке функция  имеет конечные, но не равные друг другу левый и правый пределы, т.е.
имеет конечные, но не равные друг другу левый и правый пределы, т.е.  . Разность
. Разность
 называется скачком функции в точке
называется скачком функции в точке  , т.е. скачок на
, т.е. скачок на  единиц.
единиц.
Разрыв второго рода (бесконечный разрыв).
Точка  называется точкой разрыва второго рода функции
называется точкой разрыва второго рода функции  , если в этой точке не существует хотя бы одного из односторонних пределов функции
, если в этой точке не существует хотя бы одного из односторонних пределов функции  или хотя бы один из односторонних пределов бесконечен, т.е.
или хотя бы один из односторонних пределов бесконечен, т.е.  .
.
Точка непрерывности.
Точка  является точкой непрерывности, если функция
является точкой непрерывности, если функция  определена в этой точке и если в этой точке функция
определена в этой точке и если в этой точке функция  имеет равные друг другу левый правый пределы, т.е.
имеет равные друг другу левый правый пределы, т.е.  .
.
Свойства непрерывных функций:
1. Сумма конечного числа непрерывных функций есть функция непрерывная.
2. Произведение конечного числа непрерывных функций есть функция непрерывная.
3. Частное от деления двух непрерывных функций есть функция непрерывная во всех точках, где делитель не равен нулю.
4. Каждая элементарная функция непрерывна в любой точке, в которой она определена.
Пример 1. Исследовать функцию  на непрерывность в точке
на непрерывность в точке  .
.
Решение: а) зададим  ; б) вычислим
; б) вычислим  ;
;
в)  , т.е. получили, что
, т.е. получили, что  , значит функция непрерывна.
, значит функция непрерывна.
Пример 2. Показать, что функция  имеет разрыв в точке
имеет разрыв в точке  .
.
Решение: Находим  Таким образом, функция при
Таким образом, функция при  не имеет ни левого ни правого конечного предела. Следовательно,
не имеет ни левого ни правого конечного предела. Следовательно,  является точкой разрыва второго рода.
является точкой разрыва второго рода.
Пример 3. Исследовать функцию  на непрерывность, найти точки разрыва и определить их тип.
на непрерывность, найти точки разрыва и определить их тип.
Решение: для функции  а)
а)  точка подозреваемого разрыва, т.к. в этой точке идёт смена аналитических выражений.
точка подозреваемого разрыва, т.к. в этой точке идёт смена аналитических выражений.
Б) Найти значения  для этой точки
для этой точки

 точка разрыва первого рода, скачок на
точка разрыва первого рода, скачок на  (единиц).
(единиц).
Задание для самостоятельной работы.
Вариант 1.
1.Исследовать функцию на непрерывность: а)  . б)
. б) .
.
2. Найти точки разрыва и исследовать их характер: а)  б)
б)  .
.
Вариант 2.
1.Исследовать функцию на непрерывность: а)  . б)
. б) .
.
2. Найти точки разрыва и исследовать их характер: а)  б)
б) 
3. Содержание отчёта.
3.1. Название работы.
3.2. Выполнение работы.
Практическое занятие № 7.
Вычисление производной.
Цель: Выработка навыков вычисления производной первого и второго порядка.
Требования к умениям и навыкам.
Должен знать: Определение производной первого и второго порядка, формулы производных основных элементарных функций, формулы производных суммы, произведения и частного.
Должен уметь: Применять формулы производных при выполнении упражнений.
Задание: 1. Изучить методические указания к работе, записать указанные примеры с решениями.
2. Выполнить самостоятельную работу по вариантам.
3. Сделать отчёт.
Методические указания
Краткие теоретические сведения.
Определение 1. Пусть функция f определена в некоторой окрестности точки  . Производной функции f в точке
. Производной функции f в точке  называется предел отношения приращения
называется предел отношения приращения  функции f в точке
функции f в точке  к соответствующему приращению аргумента
к соответствующему приращению аргумента  если приращение аргумента
если приращение аргумента  стремится к нулю. Обозначается производная функции
стремится к нулю. Обозначается производная функции  символами
символами
 .
.

 .
.
Определение 2. Если функция ![]() имеет производную в каждой точке
имеет производную в каждой точке ![]() своей области определения, то ее производная
своей области определения, то ее производная ![]() есть функция от
есть функция от ![]() . Функция
. Функция ![]() , в свою очередь, может иметь производную, которую называют производной второго порядка функции
, в свою очередь, может иметь производную, которую называют производной второго порядка функции ![]() (или второй производной) и обозначают символом
(или второй производной) и обозначают символом ![]() . Таким образом
. Таким образом
![]()
Геометрический смысл производной. Производная в точке x0 равна угловому коэффициенту касательной к графику функции y = f(x) в этой точке

Уравнение касательной к графику функции y = f(x) в точке x0 :
![]()
Пример: Составить уравнение касательной к параболе  .
.
Решение. Найдём производную функции  при
при  . Имеем
. Имеем  , откуда
, откуда  . Воспользуемся уравнением касательной, получим искомое уравнение касательной :
. Воспользуемся уравнением касательной, получим искомое уравнение касательной :
 .
.
Физический смысл производной.
Если точка движется вдоль оси х и ее координата изменяется по закону x(t), то мгновенная скорость точки:
![]()
Производная  от функции
от функции  , вычисленная при значении аргумента
, вычисленная при значении аргумента  , представляет собой скорость изменения этой функции относительно независимой переменной
, представляет собой скорость изменения этой функции относительно независимой переменной  в точке
в точке  .
.
В частности, если зависимость между пройденным путём s и временем t при прямолинейном движении выражается формулой  , то скорость движения в любой момент времени
, то скорость движения в любой момент времени  есть
есть  , а ускорение (т.е. скорость изменения скорости движения) есть
, а ускорение (т.е. скорость изменения скорости движения) есть  .
.
Пример: Точка движется прямолинейно по закону  (
( выражается в метрах,
выражается в метрах,  в секундах. Найти скорость и ускорение через 1 сек после начала движения.
в секундах. Найти скорость и ускорение через 1 сек после начала движения.
Решение. 1) Скорость прямолинейного движения равна производной пути по времени : 
 .
.
2) Вычислим значение скорости при  ,
,  .
.
3) Ускорение прямолинейного движения равно второй производной пути по времени: 
 .
.
4) Вычислим значение ускорения при  .
.
Ответ:  .
.
Правила дифференцирования.
1. 
2.
3.
4. .
.
Таблица производных основных элементарных функций.
1.
6.
11.
15.
18.
Найти производные функций, используя правила 1 – 4:
Пример 1. 
Решение: 
Пример 2. 
Решение: 
Пример 3. 
Решениe: 
Пример 4. 
Решение: 
Пример 5. 
Решение: 
2.Задания для самостоятельной работы.
Вариант 1.
1.Найти производную:
1.
4.
2. Точка движется прямолинейно по закону  . Найти мгновенную скорость и ускорение точки в момент времени
. Найти мгновенную скорость и ускорение точки в момент времени  с.
с.
3. Точка движется прямолинейно по закону  . Найти мгновенную скорость и ускорение точки в момент времени
. Найти мгновенную скорость и ускорение точки в момент времени  с.
с.
Вариант 2.
1.Найти производную:
1.
4.
2. Точка движется прямолинейно по закону  . Найти мгновенную скорость и ускорение точки в момент времени
. Найти мгновенную скорость и ускорение точки в момент времени  с.
с.
3. Точка движется прямолинейно по закону  . Найти мгновенную скорость и ускорение точки в момент времени
. Найти мгновенную скорость и ускорение точки в момент времени  с.
с.
3.Содержание отчёта.
3.1 Название работы.
3.2 Выполнение работы.
Практическое занятие № 8.
Производная сложной функции.
Цель: обобщить и закрепить знания о правилах дифференцирования сложных функций.
Требования к умениям и навыкам.
Должен знать: Определение производной первого и второго порядка, формулы производных основных элементарных функций, формулы производных суммы, произведения и частного.
Должен уметь: Применять формулы производных при выполнении упражнений.
Задание: 1. Изучить методические указания к работе, записать указанные примеры с решениями.
2. Выполнить самостоятельную работу по вариантам.
3. Сделать отчёт.
Методические указания
Краткие теоретические сведения.
Правила дифференцирования.
1. 
2.
3.
4. .
.
Таблица производных основных элементарных функций.
1.
6.
11.
15.
18.
Найти производные функций, используя правила 1 – 4:
Пример 1. 
Решение: 
Пример 2. 
Решение: 
Пример 3. 
Решениe: 
Пример 4. 
Решение: 
Пример 5. 
Решение: 
Пусть  и
и - дифференцируемые функции. Тогда сложная функция
- дифференцируемые функции. Тогда сложная функция  есть также дифференцируемая функция, причем
есть также дифференцируемая функция, причем
 , или
, или  (1)
(1)
Это правило распространяется на цепочку из любого количества дифференцируемых функций: производная сложной функции равна произведению производных функций, ее составляющих.
Пример
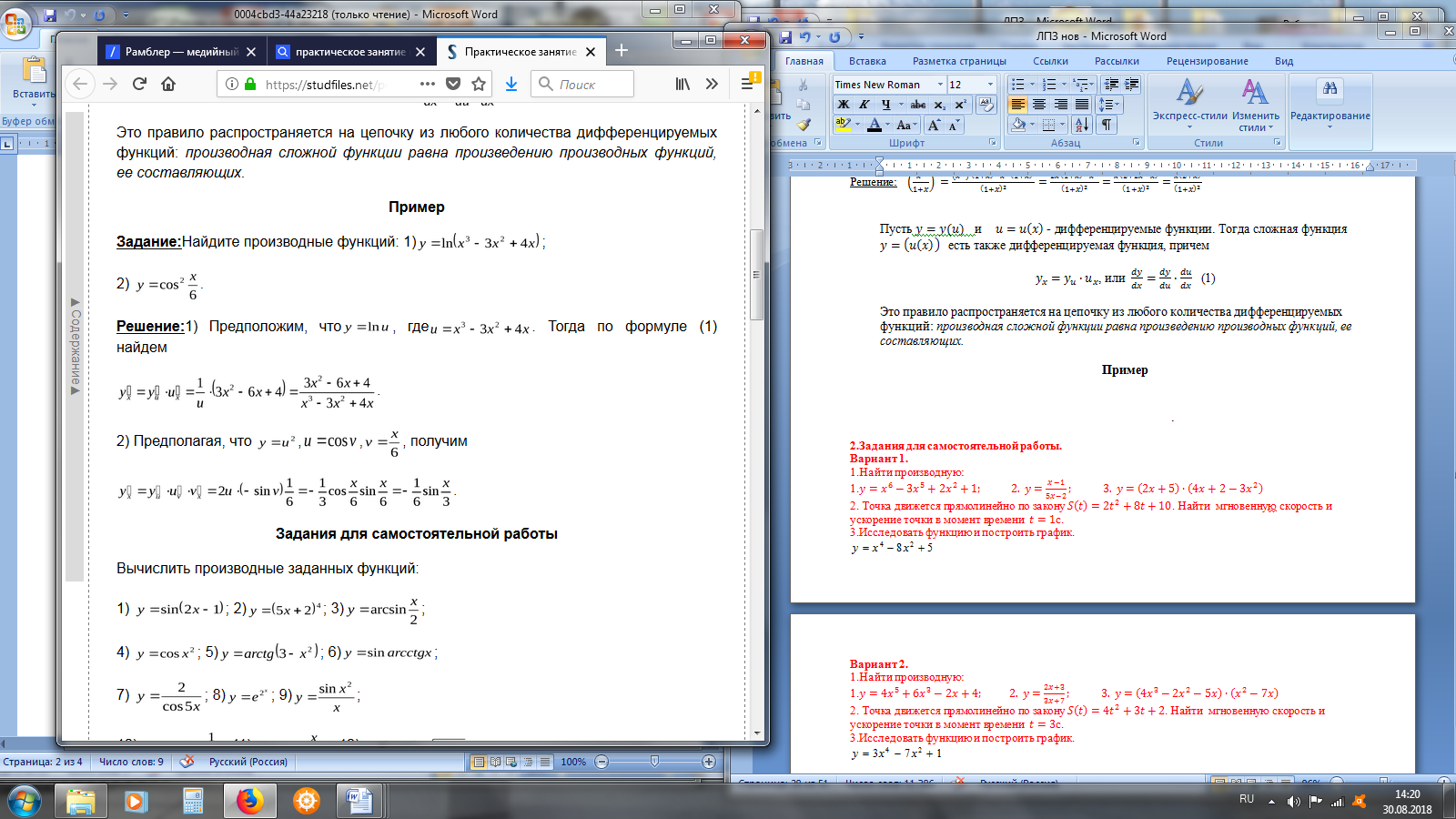 .
.
2.Задания для самостоятельной работы.
Вариант 1.
1. Найти производные сложных функций:
а) y =  б)
б) 2 в) y =
2 в) y = 
2. Определите какие из данных функций являются простыми, а какие сложными. Заполните таблицу:
| Простая функция | Сложная функция |
|
|
|
|
|
|
 ln (4x – 3)
ln (4x – 3) 


 –
– 

Вариант 2.
1. Найти производные сложных функций:
а) y = 3 cos 5x б)  в) y =
в) y = 
2. Определите какие из данных функций являются простыми, а какие сложными. Заполните таблицу:
| Простая функция | Сложная функция |
|
|
|
|
|
|

 – 2ln x 3 cos 5x
– 2ln x 3 cos 5x
 2 17
2 17 

3.Содержание отчёта.
3.1 Название работы.
3.2 Выполнение работы.
Практическое занятие № 9.
Исследование функции с помощью производной и построение графиков.
Цель: Изучить последовательность исследования функций и построения их графиков.
Требования к умениям и навыкам.
Должен знать: Определения точек максимума и минимума, правило исследования функции на экстремум с помощью первой производной. Определения выпуклости графика функции, точки перегиба графика функции; последовательность исследования функций и построение их графиков.
Должен уметь: Применять формулы производных при выполнении упражнений. Исследовать функции с помощью производных и строить их графики.
Задание: 1. Изучить методические указания к работе, записать указанные примеры с решениями.
2. Выполнить самостоятельную работу по вариантам.
3. Сделать отчёт.
Методические указания
Краткие теоретические сведения.
Правила дифференцирования.
1. 
2.
3.
4. .
.
Таблица производных основных элементарных функций.
1.
6.
11.
15.
18.
Найти производные функций, используя правила 1 – 4:
Пример 1. 
Решение: 
Пример 2. 
Решение: 
Пример 3. 
Решениe: 
Пример 4. 
Решение: 
Пример 5. 
Решение: 
Исследование функций с помощью производных.
Определение 1. Функция  монотонно убывает, если большему значению аргумента
монотонно убывает, если большему значению аргумента  соответствует меньшее значение функции. Условие убывания функции на интервале
соответствует меньшее значение функции. Условие убывания функции на интервале 
Определение 2. Функция  монотонно возрастает, если большему значению аргумента
монотонно возрастает, если большему значению аргумента  соответствует большее значение функции
соответствует большее значение функции  . Условие убывания функции на интервале
. Условие убывания функции на интервале 
Определение 3. Функция  имеет максимум (минимум) при
имеет максимум (минимум) при  =
=  , если при всех
, если при всех  достаточно близких к
достаточно близких к  , выполняется неравенство:
, выполняется неравенство: максимум,
максимум,  минимум.
минимум.
Признаки максимума:
1.
2. при переходе аргумента через
при переходе аргумента через  =
=  меняет знак с плюса на минус (с возрастания на убывание).
меняет знак с плюса на минус (с возрастания на убывание).
Признаки минимума:
1.
2. при переходе аргумента через
при переходе аргумента через  =
=  меняет знак с минуса на плюс (с убывания на прибавление). Говорят, что функция имеет экстремум в некоторой точке
меняет знак с минуса на плюс (с убывания на прибавление). Говорят, что функция имеет экстремум в некоторой точке  =
=  , если она имеет в этой точке максимум или минимум. Точки, в которых функция
, если она имеет в этой точке максимум или минимум. Точки, в которых функция  достигает экстремума, называются критическими точками первого рода.
достигает экстремума, называются критическими точками первого рода.
Пример 1. Исследовать функцию  на монотонность и экстремумы.
на монотонность и экстремумы.
Решение. Найдём производную:  . Найдём точки – «претенденты» на экстремум:
. Найдём точки – «претенденты» на экстремум: 
 . Определим знаки производной на промежутках
. Определим знаки производной на промежутках  :
:
 + 1 +
+ 1 +
Т.е. функция  возрастает на всей прямой, и
возрастает на всей прямой, и  - не экстремум. Данный пример показывает, что не все точки, в которых производная равна нулю, являются точками экстремума.
- не экстремум. Данный пример показывает, что не все точки, в которых производная равна нулю, являются точками экстремума.
Пример 2. Найти интервалы возрастания и убывания функции  и её экстремумы.
и её экстремумы.
Решение. Производная рассматриваемой функции существует при любом х и равна у' =х2 - 4х + 3 . Приравняв производную нулю и решив полученное квадратное уравнение, найдем две критические точки  = 1 и х2 = 3.
= 1 и х2 = 3.
Ось х разбивается этими точками на три интервала:  причем на каждом из них у' сохраняет знак.
причем на каждом из них у' сохраняет знак.
Определим эти знаки, например, вычислив у' в произвольных точках указанных интервалов, получим: 

Отсюда функция  возрастает на интервалах
возрастает на интервалах  убывает на интервале
убывает на интервале в точке
в точке  достигает максимального значения
достигает максимального значения  , а в точке
, а в точке  минимального значения
минимального значения .
.
Схема исследования функции.
Найти область определения D(f), указать промежутки непрерывности.
Найти область значений E(f). Определить четность и периодичность функции.
Найти «нули» функции (если это возможно).Указать промежутки знакопостоянства функции (т.е. промежутки между двумя соседними нулями или точками разрыва) и определить знаки функции на этих промежутках (если это возможно).
Найти производную функции.
Найти точки, которые могут оказаться экстремумами
Найти промежутки монотонности и точки экстремума.
По результатам проведенной работы построить график.
Пример 3. Исследовать функцию и построить ее график: 
Решение 1. Область определения функции - множество всех действительных чисел:  или
или  Функция непрерывна на всей области определения, так как является суммой элементарных функций.
Функция непрерывна на всей области определения, так как является суммой элементарных функций.
Область значений, также, множество всех действительных чисел: .
.
При ,
, ; при
; при  .
.
Нули функции: х3 - х2 - 5х + 5 = 0, х2 (х - 1) - 5(х -1) = 0, (х - 1)(х2 - 5) = 0,  .
.
В этих точках график функции пересекает ось Ох.
Точка пересечения графика функции с осью Оу: х = 0, у = 5.
Функция ни четная и ни нечетная.
Функция непериодическая.
Промежутки возрастания и убывания.
Производная функции равна: у' = Зх2 - 2х - 5 .
Критические точки:  .
.
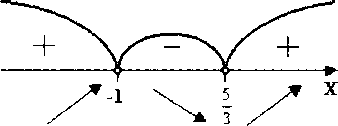
При  значит, функция возрастает на этом промежутке.
значит, функция возрастает на этом промежутке.
При  значит, функция убывает на этом промежутке.
значит, функция убывает на этом промежутке.
При  значит, функция возрастает на этом промежутке.
значит, функция возрастает на этом промежутке.
9.Максимумы и минимумы функции (экстремумы функции).
В точке  функция имеет максимум:
функция имеет максимум:  .
.
В точке 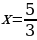 функция имеет минимум:
функция имеет минимум:  .
.
Г рафик функции.
рафик функции.
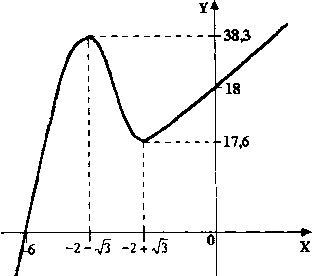
Пример 4. Исследовать функцию и построить ее график:
у = х3 +6х2 + Зх +18.
Решение 1. Область определения функции - множество всех действительных чисел,  , или
, или
( ).
).
Область значений, также множество всех действительных чисел, .
.
Функция непрерывна на всей области определения, так как представляет сумму непрерывных элементарных функций х3 , 6х2, Зx, 18.
При ,
, ; при
; при  .
.
Нули функции: х3 + 6х2 + Зх +18 = 0, х2 (х + 6) + 3(х + 6) = 0, (х2 + 3)(х + 6) = О, х2 + +3 ,
, . В этой точке график функции пересекает ось Ох.
. В этой точке график функции пересекает ось Ох.
При х = 0, у = 18, значит, график пересекает ось ординат в точке (0; 18).
Функция непериодическая.
Функция ни четная, ни нечетная.
Промежутки возрастания и убывания.
Производная функции: у' = 3х2 +12х + 3.
Критические точки:
Зх2 + 12х + 3 = 0, х2 + 4х + 1 = 0, .
.

При , значит, функция возрастает на этом промежутке.
, значит, функция возрастает на этом промежутке.
При  у' 0, значит, функция убывает на этом промежутке.
у' 0, значит, функция убывает на этом промежутке.
При  у' 0, значит, функция возрастает на этом промежутке.
у' 0, значит, функция возрастает на этом промежутке.
Максимумы и минимумы функции.
В точке 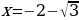 функция имеет максимум
функция имеет максимум 
В точке  функция имеет минимум
функция имеет минимум 
График функции.
2.Задания для самостоятельной работы.
Вариант 1.
Исследовать функции и построить их графики.
1) 
2) 
Вариант 2.
Исследовать функции и построить их графики.


3.Содержание отчёта.
3.1 Название работы.
3.2 Выполнение работы.
Практическое занятие № 10.
Интегрирование методом разложения.
Цель: Выработать навыки вычисления неопределённого интеграла методом непосредственного интегрирования.
Требования к умениям и навыкам. Должен знать: Определения первообразной функции, неопределенного интеграла, свойства неопределенного интеграла, простейшие формулы интегрирования, метод непосредственного интегрирования.
Должен уметь: Применять свойства неопределенного интеграла, простейшие формулы
интегрирования, метод непосредственного интегрирования.
Задание: 1. Изучить методические указания к работе, записать указанные примеры с решениями.
2.Выполнить самостоятельную работу по вариантам.
3. Сделать отчёт.
Методические указания
Краткие теоретические сведения
1. Определение: Функция F(x) называется первообразной функцией функции f(x) на отрезке [а, Ь], если в любой точке этого отрезка верно равенство:
F'(x) = f(x).
Надо отметить, что первообразных для одной и той же функции может быть бесконечно много. Они будут отличаться друг от друга на некоторое постоянное число.
F,(x) = F2(x) + C.
2.Определение: Совокупность всех первообразных функций F(x) + С для функции f(x) на некотором промежутке называется неопределённым интегралом и обозначается

где  называется подынтегральным выражением,
называется подынтегральным выражением,  - переменной интегрирования, а С – произвольной постоянной интегрирования. Процесс нахождения первообразной функции называется интегрированием. Например:
- переменной интегрирования, а С – произвольной постоянной интегрирования. Процесс нахождения первообразной функции называется интегрированием. Например:  , так как
, так как 
3.Свойства:
1. ;
;
2. ;
;
3. ;
;
4. ; где u, v, w – некоторые функции от
; где u, v, w – некоторые функции от  .
.
5. .
.
4.Метод непосредственного интегрирования. Под непосредственным интегрированием понимают способ интегрирования, при котором данный интеграл путём тождественных преобразований подынтегральной функции и применения свойств неопределённого интеграла приводятся к одному или нескольким табличным интегралам.
Формулы интегрирования:
1.  2.
2.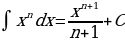 , где
, где  3.
3. 4.
4.
5. 6.
6. 7.
7. 8.
8. 
9. 10.
10. 11.
11.
12. 13.
13. 14.
14.
15.
Пример 1. Решение.  .
.
Пример 2. Решение. 
= .
.
Пример 3. Решение. 
+  .
.
Задания для самостоятельной работы.
Вариант 1.
1.Методом непосредственного интегрирования вычислить:
а) 
е) 
к)  .
.
Вариант 2.
1.Методом непосредственного интегрирования вычислить:
а) 
е) 
к)  .
.
3.Содержание отчёта.
3.1 Название работы.
3.2 Выполнение работы
Практическое занятие № 11.
Интегрирование методом замены переменной.
Цель: Выработать навыки вычисления неопределённого интеграла методом подстановки. Отработать навыки нахождения определенного интеграла.
Требования к умениям и навыкам. Должен знать: Определения первообразной функции, неопределенного интеграла, свойства неопределенного интеграла, простейшие формулы интегрирования, метод интегрирования: подстановки (замены переменной).
Должен уметь: Применять свойства неопределенного интеграла, простейшие формулы
интегрирования, методы интегрирования: подстановки (замены переменной).
Задание: 1. Изучить методические указания к работе, записать указанные примеры с решениями.
2.Выполнить самостоятельную работу по вариантам.
3. Сделать отчёт.
Методические указания
Краткие теоретические сведения
1. Определение: Функция F(x) называется первообразной функцией функции f(x) на отрезке [а, Ь], если в любой точке этого отрезка верно равенство:
F'(x) = f(x).
Надо отметить, что первообразных для одной и той же функции может быть бесконечно много. Они будут отличаться друг от друга на некоторое постоянное число.
F,(x) = F2(x) + C.
2.Определение: Совокупность всех первообразных функций F(x) + С для функции f(x) на некотором промежутке называется неопределённым интегралом и обозначается

где  называется подынтегральным выражением,
называется подынтегральным выражением,  - переменной интегрирования, а С – произвольной постоянной интегрирования. Процесс нахождения первообразной функции называется интегрированием. Например:
- переменной интегрирования, а С – произвольной постоянной интегрирования. Процесс нахождения первообразной функции называется интегрированием. Например:  , так как
, так как 
3.Свойства:
1. ;
;
2. ;
;
3. ;
;
4. ; где u, v, w – некоторые функции от
; где u, v, w – некоторые функции от  .
.
5. .
.
Формулы интегрирования:
1.  2.
2.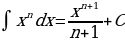 , где
, где  3.
3. 4.
4.
5. 6.
6. 7.
7. 8.
8. 
9. 10.
10. 11.
11.
12. 13.
13. 14.
14.
15.
4.Метод подстановки (замена переменной).
Сущность интегрирования методом подстановки заключается в преобразовании интеграла  в интеграл
в интеграл  , который легко вычисляется по какой – либо из основных формул интегрирования. Для нахождения
, который легко вычисляется по какой – либо из основных формул интегрирования. Для нахождения  заменяем переменную
заменяем переменную  новой переменной
новой переменной  с помощью подстановки
с помощью подстановки  . Дифференцируя это равенство, получаем
. Дифференцируя это равенство, получаем  . Подставляя в подынтегральное выражение вместо
. Подставляя в подынтегральное выражение вместо  и
и  их значения, выраженные через
их значения, выраженные через  и
и  , имеем
, имеем  . После того, как интеграл относительно новой переменной
. После того, как интеграл относительно новой переменной  будет найден, с помощью подстановки
будет найден, с помощью подстановки  он приводится к переменной
он приводится к переменной  .
.
Пример 1.  ;
;
Решение: Положим  . Продифференцируем это равенство:
. Продифференцируем это равенство:  или
или  . Заменим в интеграле
. Заменим в интеграле  .
.
Пример 2. 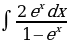
Решение: Сделав замену:  , получим
, получим  . Тогда
. Тогда  .
.
Пример 3. 
Решение: Сделав замену:  , получим
, получим  .
.
Тогда  .
.
Задания для самостоятельной работы.
Вариант 1.
.Методом подстановки вычислить:
а)  .
.
г)  .
.
Вариант 2.
Методом подстановки вычислить:
а)  .
.
г)  .
.
3.Содержание отчёта.
3.1 Название работы.
3.2 Выполнение работы
Практическое занятие № 12.
Вычисление определенного интеграла.
Цель: Отработать навыки нахождения определенного интеграла.
Требования к умениям и навыкам. Должен знать: Определения первообразной функции, неопределенного интеграла, свойства неопределенного интеграла, простейшие формулы интегрирования, методы интегрирования: непосредственный и подстановки (замены переменной).
Должен уметь: Применять свойства неопределенного интеграла, простейшие формулы
интегрирования, методы интегрирования: непосредственный и подстановки (замены переменной).
Задание: 1. Изучить методические указания к работе, записать указанные примеры с решениями.
2.Выполнить самостоятельную работу по вариантам.
3. Сделать отчёт.
Методические указания
Краткие теоретические сведения
Определенный интеграл, его свойства и вычисление
Определенный интеграл вычисляется по формуле Ньютона-Лейбница:
 = F(a)-F(b)
= F(a)-F(b)
 - соответственно верхний и нижний пределы интегрирования, они пишутся и читаются снизу вверх, а в формулу подставляются сверху вниз!)
- соответственно верхний и нижний пределы интегрирования, они пишутся и читаются снизу вверх, а в формулу подставляются сверху вниз!)
Основные свойства определенного интеграла:
При перестановке пределов интегрирования изменяется знак интеграла:

Отрезок интегрирования можно разбивать на части:

Определенный интеграл от алгебраической суммы функций равен алгебраической сумме их определенных интегралов.
Постоянный множитель можно выносить за знак интеграла.
Пример 1.
 =
= =27-8=19.
=27-8=19.
Вычисления определённого интеграла методом введения новой переменной.

Пример 2.
 =
= =
= =
= =
=
Пример 3.
 = -
= -  =-
=- (
( )=-
)=-
Вычисление определенного интеграла по частям:
Используем формулу:
 -
-
Пример 4.
 =
= -
- +
+ =(
=( )+
)+ -1-1=
-1-1= -2;
-2;
Пример 5.
 =-6xctgx
=-6xctgx +
+ =-6·
=-6· -6·
-6· +ln|sinx|
+ln|sinx| =π
=π + ln|sin
+ ln|sin |- ln|sin
|- ln|sin |= π
|= π + ln1- ln
+ ln1- ln = π
= π + 0+ln2= π
+ 0+ln2= π +ln2
+ln2
Задания для самостоятельной работы.
Вариант 1.

 3
3 4
4
Вариант 2.
 2
2 3
3 4
4
3.Содержание отчёта.
3.1 Название работы.
3.2 Выполнение работы
Практическое занятие № 13.
Вычисление площади плоских фигур.
Цель: Выработать навыки вычисления неопределённого интеграла методом непосредственного интегрирования и методом подстановки. Отработать навыки нахождения определенного интеграла. Научиться находить площади плоских фигур.
Требования к умениям и навыкам. Должен знать: Определения первообразной функции, неопределенного интеграла, свойства неопределенного интеграла, простейшие формулы интегрирования, методы интегрирования: непосредственный и подстановки (замены переменной). Формулы для вычисления площадей плоских фигур.
Должен уметь: Применять свойства неопределенного интеграла, простейшие формулы
интегрирования, методы интегрирования: непосредственный и подстановки (замены переменной). Применять формулы для вычисления площадей плоских фигур при решении практических задач.
Задание: 1. Изучить методические указания к работе, записать указанные примеры с решениями.
2.Выполнить самостоятельную работу по вариантам.
3. Сделать отчёт.
Методические указания
Краткие теоретические сведения
Формулы интегрирования:
1.  2.
2.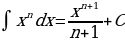 , где
, где  3.
3. 4.
4.
5. 6.
6. 7.
7. 8.
8. 
9. 10.
10. 11.
11.
12. 13.
13. 14.
14.
15.
Определение. Разность F (b) – F (a) называется интегралом от функции f (x) на отрезке [ a ; b ] и обозначается так: ![]() = F (b) – F (a) – формула Ньютона-Лейбница.
= F (b) – F (a) – формула Ньютона-Лейбница.
Геометрический смысл интеграла.

Площадь криволинейной трапеции, ограниченной графиком непрерывной положительной на промежутке [ a ; b ] функции f (x), осью Ох и прямыми х=а и х= b:
![]() .
.
Вычисление площадей с помощью интеграла.
1.Площадь фигуры, ограниченной графиком непрерывной отрицательной на промежутке [ a ; b ] функции f (x), осью Ох и прямыми х=а и х= b :

2.Площадь фигуры, ограниченной графиками непрерывных функций f (x), ![]() и прямыми х=а, х= b :
и прямыми х=а, х= b :

3.Площадь фигуры, ограниченной графиками непрерывных функций f (x) и ![]() :
:

4.Площадь фигуры, ограниченной графиками непрерывных функций f (x), ![]() и осью Ох:
и осью Ох:

П ример 1. Вычислить площадь фигуры, ограниченной линиями
ример 1. Вычислить площадь фигуры, ограниченной линиями  ,
,  .
.
Решение. Находим точки пересечения заданных линий.
Для этого решаем систему уравнений: 
Для нахождения абсцисс точек пересечения заданных линий решаем уравнение:  или
или  .
.
Находим: x1 = – 2, x2 = 4. Итак, данные линии, представляющие собой параболу и прямую, пересекаются в точках A(-2; 0), B(4; 6).
Э ти линии образуют замкнутую фигуру, площадь которой вычисляем по указанной выше формуле:
ти линии образуют замкнутую фигуру, площадь которой вычисляем по указанной выше формуле:
 .
.
По формуле Ньютона-Лейбница находим:
 .
.
Пример 2. Найти площадь фигуры, ограниченной линиями  и
и  .
.
Решение. Найдем точки пересечения линий  ,
,  , приравнивая ординаты линий:
, приравнивая ординаты линий:  или
или  . Находим корни x1 = – 1 , x2 = 3 и соответствующие им ординаты y1 = 2, y2 = – 2.
. Находим корни x1 = – 1 , x2 = 3 и соответствующие им ординаты y1 = 2, y2 = – 2.
По формуле площади фигуры получаем


Пример 3. Определить площадь, ограниченную параболой y = x2 + 1 и прямой x + y = 3.
Решение.
Решая систему уравнений  находим абсциссы точек пересечения x1 = – 2 и x2 = 1.
находим абсциссы точек пересечения x1 = – 2 и x2 = 1.
Полагая y2 = 3 – x и y1 = x2 + 1, на основании формулы  получаем
получаем 
П ример 4. Вычислить объем тела, полученного вращением вокруг оси Ox фигуры, ограниченной параболами y = x2 и x = y2.
ример 4. Вычислить объем тела, полученного вращением вокруг оси Ox фигуры, ограниченной параболами y = x2 и x = y2.
Решение.
Решим систему уравнений




и получим x1 = 0, x2 = 1, y1 = 0, y2 = 1, откуда точки пересечения кривых O(0; 0), B(1; 1). Как видно на рисунке, искомый объем тела вращения равен разности двух объемов, образованных вращением вокруг оси Ox криволинейных трапеций OCBA и ODBA:

Пример 5. Вычислить площадь, ограниченную осью Ox и синусоидой y = sin x на отрезках:
а) [0, π]; б) [0, 2π].
Р ешение.
ешение.
а) На отрезке [0, π] функция sin x сохраняет знак, и поэтому по формуле  , полагая y = sin x, находим
, полагая y = sin x, находим
 .
.
б) На отрезке [0, 2π], функция sin x меняет знак. Для корректного решения задачи, необходимо отрезок [0, 2π] разделить на два [0, π] и [π, 2π], в каждом из которых функция сохраняет знак.
По правилу знаков, на отрезке [π, 2π] площадь берется со знаком минус.
В итоге, искомая площадь равна

Задания для самостоятельной работы.
Вариант 1.
Вычислить площадь фигур, ограниченных линиями: а) 
б)  . в)
. в)  г)
г)  .
.
Вариант 2.
Вычислить площадь фигур, ограниченных линиями: а) 
б)  . в)
. в)  г)
г)  .
.
3.Содержание отчёта.
3.1 Название работы.
3.2 Выполнение работы
Практическое занятие № 15.
Вычисление вероятностей событий.
Цель: Продолжить формирование знаний, умений и навыков по вычислению вероятностей событий.
Требования к умениям и навыкам.
Должен знать: Определение, свойства вероятностей событий, сумму и произведение вероятностей событий.
Должен уметь: Применять теоретические знания при решении практических задач.
Задание: 1. Изучить методические указания к работе, записать указанные примеры с решениями.
2. Выполнить самостоятельную работу по вариантам.
3. Сделать отчёт.
Методические указания.
Краткие теоретические сведения.
1. Вычисление вероятностей событий.
Наблюдаемые нами события (явления) можно подразделить на следующие три вида: достоверные, невозможные и случайные.
Событие называется достоверным, если оно обязательно наступит в результате данного опыта; достоверное событие обозначается через (омега).
Событие называется невозможным, если оно заведомо не произойдет в результате данного опыта; невозможное событие обозначается через Ø (пустое множество).
Случайным событием (или просто: событием) называется такой исход опыта (испытания, эксперимента, наблюдения), который может произойти или не произойти.
Два события называются несовместными, если появление одного из них исключает появление другого события в одном и том же опыте; в противном случае события называются совместными.
События называют равновозможными, если есть основание считать, что ни одно из них не является более возможным, чем другое. (т.е. все события имеют равные «шансы»).
Противоположным событию А называется событие ![]() , которое происходит тогда и только тогда, когда не происходит событие А.
, которое происходит тогда и только тогда, когда не происходит событие А.
Несколько событий образуют полную группу, если в результате испытания появится хотя бы одно из них. Другими словами, появление хотя бы одного из событий полной группы есть достоверное событие. В частности, если события, образующие полную группу, попарно несовместны, то в результате испытания появится одно и только одно из этих событий.
Вероятность события численно характеризует степень возможности его появления в рассматриваемом опыте. Вероятностью события А называют отношение числа благоприятствующих этому событию исходов к общему числу всех равновозможных несовместных элементарных исходов, образующих полную группу:
![]()
где m – число элементарных исходов, благоприятствующих А;
n – число всех возможных элементарных исходов испытания.
Свойства:
Вероятность достоверного события равна единице: P(А)=1
Вероятность невозможного события равна нулю: P(А)=0
Вероятность случайного события есть положительное число, заключенное между нулем и единицей:  .
.
Вероятности события А и противоположного ему события определяются равенством: ![]()
Операции над событиями
Суммой событий А и В называют событие  (или другое обозначение
(или другое обозначение  - объединение), состоящее в том, что произошло либо А, либо В, либо оба события одновременно (рис. 1); в другой формулировке - наступление хотя бы одного из этих событий А или В.
- объединение), состоящее в том, что произошло либо А, либо В, либо оба события одновременно (рис. 1); в другой формулировке - наступление хотя бы одного из этих событий А или В.
Произведением событий А и В называют событие  (или другое обозначение
(или другое обозначение  - пересечение), состоящее в одновременном наступлении этих событий А и В (рис. 2).
- пересечение), состоящее в одновременном наступлении этих событий А и В (рис. 2).
|
|
|
| Рис. 1. Сумма событий | Рис. 2. Произведение событий |
Вероятность суммы событий
Теорема сложения вероятностей несовместных событий:
![]()
Теорема сложения вероятностей совместных событий:
![]()
Вероятность произведения событий
Теорема умножения вероятностей независимых событий:
![]()
Теорема умножения вероятностей зависимых событий:
![]() ,
,
![]() - условная вероятность события
- условная вероятность события ![]() при условии, что произошло событие
при условии, что произошло событие ![]() ,
,
![]() - условная вероятность события
- условная вероятность события ![]() при условии, что произошло событие
при условии, что произошло событие ![]() .
.
Событие А называется частным случаем события В, если при наступлении А наступает и В. То, что А является частным случаем В, записываем ![]() .
.
События А и В называются равными, если каждое из них является частным случаем другого. Равенство событий А и В записываем А = В.
Суммой событий А и В называется событие А + В, которое наступает тогда и только тогда, когда наступает хотя бы одно из событий: А или В.
Теорема о сложении вероятностей. Вероятность появления одного из двух несовместных событий равна сумме вероятностей этих событий.
![]()
Заметим, что сформулированная теорема справедлива для любого числа несовместных событий:
![]() .
.
Если случайные события ![]() образуют полную группу несовместных событий, то имеет место равенство
образуют полную группу несовместных событий, то имеет место равенство
![]() .
.
Произведением событий А и В называется событие АВ, которое наступает тогда и только тогда, когда наступают оба события: А и В одновременно. Случайные события А и B называются совместными, если при данном испытании могут произойти оба эти события.
Теорема о сложении вероятностей 2. Вероятность суммы совместных событий вычисляется по формуле
![]() .
.
События событий А и В называются независимыми, если появление одного из них не меняет вероятности появления другого. Событие А называется зависимым от события В, если вероятность события А меняется в зависимости от того, произошло событие В или нет.
Теорема об умножении вероятностей. Вероятность произведения независимых событий А и В вычисляется по формуле:
![]() .
.
Пример. В первом ящике 1 белый и 5 черных шаров, во втором 8 белых и 4 черных шара. Из каждого ящика вынули по шару. Найти вероятность того, что один из вынутых шаров белый, а другой – черный.
Решение. Обозначим события: А – вынули белый шар из первого ящика,
![]() ;
;
![]() - вынули черный шар из первого ящика,
- вынули черный шар из первого ящика,
![]() ;
;
В – белый шар из второго ящика,
![]() ;
;
![]() - черный шар из второго ящика,
- черный шар из второго ящика,
![]() .
.
Нам нужно, чтобы произошло одно из событий ![]() или
или ![]() . По теореме об умножении вероятностей
. По теореме об умножении вероятностей
![]() ,
, ![]() .
.
Тогда искомая вероятность по теореме сложения будет
![]() .
.
Пример. Вероятность попадания в цель у первого стрелка 0,8, у второго – 0,9. Стрелки делают по выстрелу. Найти вероятность: а) двойного попадания; б) двойного промаха, в) хотя бы одного попадания; г) одного попадания.
Решение.
Пусть А – попадание первого стрелка, ![]() ;
;
В – попадание второго стрелка, ![]() .
.
Тогда ![]() - промах первого,
- промах первого, ![]() ;
;
![]() - промах второго,
- промах второго, ![]() .
.
Найдем нужные вероятности.
а) АВ – двойное попадание, ![]()
б) ![]()
![]() – двойной промах,
– двойной промах, ![]() .
.
в) А+В – хотя бы одно попадание,
![]() .
.
г) ![]() – одно попадание,
– одно попадание,
![]() .
.
Пример. Студент разыскивает нужную ему формулу в трех справочниках. Вероятности того, что формула содержится в первом, втором и третьем справочниках равны 0,6; 0,7 и 0,8. Найти вероятности того, что формула содержится 1) только в одном справочнике; 2) только в двух справочниках; 3) во всех трех справочниках.
Решение.
А – формула содержится в первом справочнике;
В – формула содержится во втором справочнике;
С – формула содержится в третьем справочнике.
Воспользуемся теоремами сложения и умножения вероятностей.
1. ![]()
2. ![]() .
.
3. ![]()
Пусть в результате испытания могут появиться n событий, независимых в совокупности, либо некоторые из них (в частности, только одно или ни одного), причем вероятности появления каждого из событий известны. Как найти вероятность того, что наступит хотя бы одно из этих событий? Например, если в результате испытания могут появиться три события, то появление хотя бы одного из этих событий означает наступление либо одного, либо двух, либо трех событий. Ответ на поставленный вопрос дает следующая теорема.
Теорема. Вероятность появления хотя бы одного из событий ![]() , независимых в совокупности, равна разности между единицей и произведением вероятностей противоположных событий
, независимых в совокупности, равна разности между единицей и произведением вероятностей противоположных событий
![]()
Если события ![]() имеют одинаковую вероятность
имеют одинаковую вероятность ![]() , то формула принимает простой вид:
, то формула принимает простой вид:
![]() .
.
Пример. Вероятности попадания в цель при стрельбе из трех орудий таковы: p1 = 0,8; p2 = 0,7; p3 = 0,9. Найти вероятность хотя бы одного попадания (событие А) при одном залпе из всех орудий.
Решение. Вероятность попадания в цель каждым из орудий не зависит от результатов стрельбы из других орудий, поэтому рассматриваемые события ![]() (попадание первого орудия),
(попадание первого орудия), ![]() (попадание второго орудия) и
(попадание второго орудия) и ![]() (попадание третьего орудия) независимы в совокупности.
(попадание третьего орудия) независимы в совокупности.
Вероятности событий, противоположных событиям ![]() ,
, ![]() и
и ![]() (т. е. вероятности промахов), соответственно равны:
(т. е. вероятности промахов), соответственно равны:
![]() ,
, ![]() ,
, ![]()
Искомая вероятность ![]() .
.
Пример. В типографии имеется 4 плоскопечатных машины. Для каждой машины вероятность того, что она работает в данный момент, равна 0,9. Найти вероятность того, что в данный момент работает хотя бы одна машина (событие А).
Решение. События "машина работает" и "машина не работает" (в данный момент) — противоположные, поэтому сумма их вероятностей равна единице: ![]()
Отсюда вероятность того, что машина в данный момент не работает, равна ![]()
Искомая вероятность ![]()
Так как полученная вероятность весьма близка к единице, то на основании следствия из принципа практической невозможности маловероятных событий мы вправе заключить, что в данный момент работает хотя бы одна из машин.
Пример. Вероятность того, что при одном выстреле стрелок попадает в цель, равна 0,4. Сколько выстрелов должен произвести стрелок, чтобы с вероятностью не менее 0,9 он попал в цель хотя бы один раз?
Решение. Обозначим через А событие "при n выстрелах стрелок попадает в цель хотя бы один раз". События, состоящие в попадании в цель при первом, втором выстрелах и т. д., независимы в совокупности, поэтому применима формула ![]() .
.
Приняв во внимание, что, по условию, ![]() (следовательно,
(следовательно, ![]() ), получим
), получим

Прологарифмируем это неравенство по основанию 10:

Итак, ![]() , т.е. стрелок должен произвести не менее 5 выстрелов.
, т.е. стрелок должен произвести не менее 5 выстрелов.
Вероятность противоположного события ![]() определяется по формуле: р(
определяется по формуле: р(![]() )=1- р(А).
)=1- р(А).
Для несовместных событий вероятность суммы двух событий вычисляется по формуле:
р(А+В)=р(А)+р(В).
Пример. Завод производит 85% продукции первого сорта и 10% - второго. Остальные изделия считаются браком. Какова вероятность, что взяв наудачу изделие, мы получим брак?
Решение. Р=1-(0,85+0,1)=0,05.
Вероятность суммы двух любых случайных событий равна р(А+В) = р(А)+р(В)-р(АВ).
Пример. Из 20 студентов 5 человек сдали на двойку экзамен по истории, 4 – по английскому языку, причём 3 студента получили двойки по обоим предметам. Каков процент студентов в группе, не имеющих двоек по этим предметам?
Решение. Р = 1 - (5/20 + 4/20 - 3/20) = 0,7 (70%)
Задание для самостоятельной работы.
Вариант 1.
Покупатель может приобрести акции трех компаний: A, B и C. Надежность первой оценивается экспертами на уровне 90 %, второй – 85 % и третьей – 91 %. Чему равна вероятность того, что а) только одна компания в течение года станет банкротом; б) по крайней мере две компании обанкротятся?
Рабочий обслуживает три станка, работающих независимо друг от друга. Вероятность того, что за смену первый станок не потребует внимания рабочего, равна 0,9, второй – 0,8, третий – 0,75. Найти вероятность того, что за смену: а) только третий станок потребует внимания; б) хотя бы один станок потребует внимания рабочего.
3. Агрегат имеет четыре двигателя и способен функционировать, если работают, по крайней мере, два из них. Вероятность выйти из строя первому двигателю – 0,01; второму – 0,02; третьему – 0,03 и четвертому – 0,04. Какова вероятность выйти из строя агрегату?
4. Предприятием послана автомашина за различными материалами на четыре базы. Вероятность наличия нужного материала на первой базе равна 0,9, на второй – 0,95, на третьей – 0,8, на четвертой – 0,6. Найти вероятность того, что только на одной базе не окажется нужного материала.
Вариант 2.
Вероятность получить высокие дивиденды по акциям на первом предприятии – 0,2, на втором – 0,35, на третьем – 0,15. Определить вероятность того, что акционер, имеющий акции всех предприятий, получит высокие дивиденды: а) на всех предприятиях; б) только на одном предприятии; в) хотя бы на оном предприятии.
Вероятность потери письма в почтовом отделении равна 0,03, а телеграммы – 0,01. Отправлено два письма и одна телеграмма. Какова вероятность того, что дойдет: а) только телеграмма; б) хотя бы одно из отправлений?
Станция метрополитена оборудована тремя независимо работающими эскалаторами. Вероятность безотказной работы в течение дня для первого эскалатора равна 0,9, для второго – 0,95, для третьего – 0,85. Найти вероятность того, что в течение дня произойдет поломка не более одного эскалатора.
Произведен залп по цели из трех орудий. Вероятности попадания в цель из каждого орудия соответственно равны 0,6; 0,7; 0,8. Найти вероятность поражения цели: а) хотя бы один раз; б) только один раз.
3.Содержание отчёта.
3.1 Название работы.
3.2 Выполнение работы.
Практическое занятие № 16.
Исследование вариационных рядов.
Цель: Исследованию вариационных рядов.
Требования к умениям и навыкам.
Должен знать: Определение вариационных рядов и основные числовые характеристики вариационных рядов.
Должен уметь: Применять теоретические знания при решении практических задач.
Задание: 1. Изучить методические указания к работе, записать указанные примеры с решениями.
2. Выполнить самостоятельную работу по вариантам.
3. Сделать отчёт.
Методические указания.
Краткие теоретические сведения.
Исследование вариационных рядов.
Вариационными рядами называют ряды распределения, построенные по количественному признаку. Любой вариационный ряд состоит из двух элементов: вариантов и частот. Вариантами называются отдельные значения признака, которые он принимает в вариационном ряду, то есть конкретное значение варьирующего признака.
Частотами называются численности отдельных вариант или каждой группы вариационного ряда, то есть это числа, которые показывают, как часто встречаются те или иные варианты в ряду распределения. Сумма всех частот определяет численность всей совокупности, ее объем. Частостями называются частоты, выраженные в долях единицы или в процентах к итогу. Соответственно сумма частостей равна 1 или 100%.
В зависимости от характера вариации признака различают три формы вариационного ряда: ранжированный ряд, дискретный ряд и интервальный ряд.
Ранжированный вариационный ряд - это распределение отдельных единиц совокупности в порядке возрастания или убывания исследуемого признака. Ранжирование позволяет легко разделить количественные данные по группам, сразу обнаружить наименьшее и наибольшее значения признака, выделить значения, которые чаще всего повторяются.
Дискретный вариационный ряд характеризует распределение единиц совокупности по дискретному признаку, принимающему только целые значения. Например, тарифный разряд, количество детей в семье, число работников на предприятии и др.
Если признак имеет непрерывное изменение, которые в определенных границах могут принимать любые значения («от - до»), то для этого признака нужно строить интервальный вариационный ряд. Например, размер дохода, стаж работы, стоимость основных фондов предприятия и др.
Одной из основных числовых характеристик вариационного ряда является средняя арифметическая. Существует две формулы расчёта средней арифметической: простая и взвешенная. Простую среднюю арифметическую обычно используют, когда данные наблюдения не сведены в вариационный ряд либо все частоты равны единице или одинаковы  , где
, где  -е значение признака;
-е значение признака;  объём ряда (число наблюдений, число значений признака).
объём ряда (число наблюдений, число значений признака).
Если частоты отличны друг от друга, расчёт производится по формуле средней арифметической взвешенной  , где
, где  -е значение признака;
-е значение признака;  -го значения признака; k – число его значений (вариантов).
-го значения признака; k – число его значений (вариантов).
При расчёте средней арифметической в качестве весов могут выступать и частости, тогда формула расчёта средней арифметической взвешенной примет вид:  , где
, где  -е значение признака;
-е значение признака;  -го значения признака; k – число его значений (вариантов).
-го значения признака; k – число его значений (вариантов).
Дисперсию можно рассчитать по простой и взвешенной формулам, имеющим вид:  ;
;
 .
.
Среднее квадратическое отклонение рассчитывается по формуле  .
.
Медиана — это значение признака, которое лежит в основе ранжированного ряда и делит этот ряд на две равные по численности части.
Медиана (Ме) - величина признака, занимающая серединное положение в вариационном ряду. Она делит ряд на две равные части по числу наблюдений. При этом существуют особенности определения медианы для нечетного и четного рядов. В первом случае ею будет серединная или центральная варианта, которую можно определить по формуле:
Во втором случае за медиану принимают среднее значение (полу сумму) двух центральных вариант. Например, в ряду 2, 5, 6, 9, 11, 12, 15, 16 центральными вариантами будут 9 и 11. Отсюда:
Медиана в этом случае будет равна 10.
Средняя арифметическая величина (М) определяется как отношение суммы значений всех вариант вариационного ряда к общему их количеству.
Графическое представление рядов распределения
Большое значение для наглядного представления вариационных рядов имеет их графическое изображение. Рассмотрим два вида графиков: полигон и гистограмму.
Для того чтобы данные разных наблюдений и исследований были сравнимы между собой, при построении графиков используют относительные частоты (частости). Сумма частостей по всем вариантам равна единице:
![]()
Полигон строят из отрезков, соединяющих точки, координатами которых являются значения вариантов X i , и соответствующие частости m i / n.
В том случае, когда вариационный ряд является интервальным, в качестве значений вариантов X i , следует рассматривать середины интервалов.
При построении гистограммы над каждым значением варианта строится прямоугольник, высота которого пропорциональна соответствующей частости. Точнее, высота равна ![]() , где
, где ![]() – ширина интервала.
– ширина интервала.
На следующих рисунках показан в виде полигона и гистограммы вариационный ряд, отражающий распределение осужденных за тяжкие телесные повреждения по возрасту.
Табличное и графическое представления вариационных рядов помогают выявить характерные особенности изучаемых социально-правовых явлений, найти максимальные и минимальные значения частот, дать им объяснение применительно к соответствующим признакам, оценить устойчивость названных явлений, определить тенденции развития.
Полигон
Гистограмма

Табличное и графическое представления дают возможность определить целый ряд числовых характеристик вариационных рядов, которые важны при принятии оперативных, тактических и стратегических решений в деятельности служб и подразделений органов внутренних дел. Например, анализ данных по возрасту осужденных приводит к выводу, что пик криминальной активности при совершении тяжких телесных повреждений приходится на 18-19 лет, а затем частота совершения указанных преступлений постоянно снижается и к 26 годам составляет 10% от максимальной. Выработка окончательных решений по результатам дальнейшего анализа требует привлечения обширной социально-психологической и демографической информации.
Пример. При обследовании 50 членов семей рабочих и служащих установлено следующее количество членов семьи: 5;3;2;1;4;6;3;7;9;1;3;2;5;6;8;2;5;2;3;6;8;3;4;4;5;6;5;47;5;6;4;8;7;4;5;7;8;6;5;7;5;6;6;7;3;4;6;5;4.
1) Составьте вариационный ряд распределения частот.
2) Постройте полигон распределения частот.
3) Определите средний размер (среднее число членов) семьи.
4) Охарактеризуйте колеблемость размера семьи с помощью показателей вариации (дисперсии, среднего квадратического отклонения).
Решение. 1) В данной задаче изучаемый признак является дискретно варьирующим, так как размер семей не может отличаться друг от друга менее чем на одного человека. Следовательно, необходимо построить дискретный вариационный ряд. Чтобы сделать это, необходимо подсчитать, сколько раз встречаются те или иные значения признака, и расположить их в порядке возрастания или убывания. Значение изучаемого признака – размер семьи – обозначим  , частоты
, частоты  . Произведем упомянутые расчёты и запишем их результаты в таблицу.
. Произведем упомянутые расчёты и запишем их результаты в таблицу.
|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|
| 2 | 4 | 6 | 8 | 10 | 9 | 6 | 4 | 1 |
2) Дискретный вариационный ряд можно представить графически, построив полигон частот или частостей.

3) Рассчитаем средний размер (среднее число членов) семьи. Так как частоты отличны друг от друга, расчёт средней арифметической произведём по формуле  .
.
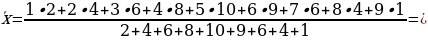
 .
.
Средний размер семьи – 5,06 чел.
4) Так как частоты неодинаковы, для расчёта дисперсии размера семьи используем формулу  .
.
 =
=
 .
.
 .
.
Найдём среднее квадратическое отклонение размера семьи по формуле 
= 1,9226.
Среднее квадратическое отклонение размера семьи – 1,9226 чел.
Задание для самостоятельной работы.
Вариант 1.
1. Дан вариационный ряд: 1;3;5;4;1;2;4;5;1;2;1;3;3;5;5;4;2;3;3;4;5;5;1;1;2.
1) Проранжировать ряд.
2) Найти медиану.
3) Построить таблицу относительных частот и график относительных частот.
4) Найти среднее арифметическое значение.
2. Дан вариационный ряд: 1;3;5;4;1;1;4;5;1;2;2;3;3;5;5;4;2;3;4;4;2;3;5;1;1.
1) Проранжировать ряд.
2) Найти медиану.
3) Построить таблицу относительных частот и график относительных частот.
4) Найти среднее арифметическое значение.
Вариант 2.
1. Дан вариационный ряд: 1;3;5;4;1;2;4;5;1;2;5;3;3;5;5;4;2;3;1;2;2;4;4;3;5.
1) Проранжировать ряд.
2) Найти медиану.
3) Построить таблицу относительных частот и график относительных частот.
4) Найти среднее арифметическое значение.
2.Дан вариационный ряд: 1;3;5;4;1;2;4;5;1;2;5;3;3;5;5;4;2;3;1;2;2;4;4;3;3.
1) Проранжировать ряд.
2) Найти медиану.
3) Построить таблицу относительных частот и график относительных частот.
4) Найти среднее арифметическое значение.
3.Содержание отчёта.
3.1 Название работы.
3.2 Выполнение работы.
Практическое занятие № 17.
Решение задач с использованием понятия множества и операций над ними.
Цель: Отработка навыков операций над множествами. Использование законов операций над множествами при решении практических задач.
Требования к умениям и навыкам.
Должен знать: Понятия множества, пустого множества, элементов множества; условие равенства множеств; определения подмножества, дополнения множества. Операции над множествами, законы операций над множествами.
Должен уметь: Производить операции над множествами, строить диаграммы Венна для иллюстрации операций над множествами.
Задание:
1. Изучить теоретический материал;
2. Рассмотреть примеры с решениями, записать их в тетрадь;
3. выполнить самостоятельную работу по вариантам;
4. Сделать отчёт.
Методические указания.
Краткие теоретические сведения.
1 . В математике множеством называют совокупность, набор каких – либо предметов (объектов). Предметы, составляющие множество, называются его элементами. То, что элемент
. В математике множеством называют совокупность, набор каких – либо предметов (объектов). Предметы, составляющие множество, называются его элементами. То, что элемент входит в множество A, записывается так:
входит в множество A, записывается так:  (
( принадлежит множеству
принадлежит множеству  ). Запись
). Запись  означает, что элемент
означает, что элемент  не принадлежит множеству
не принадлежит множеству  . Множество, не содержащее ни одного элемента, называется пустым и обозначается символом О. Примерами пустых множеств могут служить:
. Множество, не содержащее ни одного элемента, называется пустым и обозначается символом О. Примерами пустых множеств могут служить:
а) множество действительных чисел, являющихся корнями уравнения  ;
;
б) множество треугольников, сумма углов которых отлична от 
в) множество решений системы уравнений 
2. Если  два множества, то запись
два множества, то запись  означает, что они состоят из одних и тех же элементов. Если каждый элемент множества
означает, что они состоят из одних и тех же элементов. Если каждый элемент множества  является в то же время элементом множества
является в то же время элементом множества  , то говорят, что A - подмножество в
, то говорят, что A - подмножество в  , и пишут
, и пишут  . Приведем примеры подмножеств:
. Приведем примеры подмножеств:
а) множество учеников 10 класса данной школы есть подмножество множества всех учеников этой школы;
б) множество жителей Москвы является подмножеством множества жителей России;
в) множество всех квадратов есть подмножество множества всех прямоугольников.
Если одновременно с отношением  имеет место отношение
имеет место отношение  , то
, то  . То есть, если одновременно
. То есть, если одновременно  есть подмножество
есть подмножество  и
и  есть подмножество
есть подмножество  , то такие два множества равны.
, то такие два множества равны.
Диаграмма Венна – это замкнутая линия, внутри которой расположены элементы данного множества, а снаружи – элементы, не принадлежащие этому множеству.
Пусть нам дано какое – либо множество E. Мы будем рассматривать всевозможные подмножества данного множества E. Исходное множество E в таком случае называют универсальным множеством. В качестве примера возьмём множество книг. В это множество входят подмножества научных, художественных книг, книг по искусству; среди научных книг есть подмножества книг по математике, химии, биологии и т.д. Множество всех книг – это универсальное множество, содержащее в себе различные подмножества книг.
3. Объединением C двух множеств  называется множество, состоящее из всех элементов, принадлежащих множеству
называется множество, состоящее из всех элементов, принадлежащих множеству  или множеству
или множеству  . Обозначается это так:
. Обозначается это так:  . Объединение часто называют суммой множеств. Объединение трёх и более множеств определяется аналогично. На рисунках заштрихованные множества – это объединение двух и трёх множеств, соответственно.
. Объединение часто называют суммой множеств. Объединение трёх и более множеств определяется аналогично. На рисунках заштрихованные множества – это объединение двух и трёх множеств, соответственно.

Примеры: а) Обозначим через  множество целых чисел, через
множество целых чисел, через  множество чётных чисел. Тогда
множество чётных чисел. Тогда  есть множество
есть множество  , то есть
, то есть  .
.
б) Обозначим через  множество успевающих учеников в классе, через
множество успевающих учеников в классе, через  множество девочек в этом классе и через C множество неуспевающих мальчиков. Тогда
множество девочек в этом классе и через C множество неуспевающих мальчиков. Тогда  является множеством всех учащихся этого класса. Множества
является множеством всех учащихся этого класса. Множества  имеют общие элементы – успевающих девочек.
имеют общие элементы – успевающих девочек.
Пересечением C двух множеств  называется множество, состоящее из элементов, принадлежащих множеству
называется множество, состоящее из элементов, принадлежащих множеству  и множеству
и множеству  одновременно. Обозначают это так:
одновременно. Обозначают это так:  . Пересечение трёх и более множеств определяется аналогично. На рисунках заштрихованные множества – это пересечение двух и трёх множеств соответственно.
. Пересечение трёх и более множеств определяется аналогично. На рисунках заштрихованные множества – это пересечение двух и трёх множеств соответственно.
Примеры: а) Термин «пересечение» по существу геометрического происхождения. Пересечением прямой и плоскости, если прямая не параллельна плоскости, является их единственная общая точка. Если прямая и плоскость параллельны, то пересечение этих множеств пусто. Если же прямая лежит на плоскости, то их пересечение совпадает с множеством точек этой прямой.
б) Пусть  - множество мальчиков, обучающихся в данной школе, а
- множество мальчиков, обучающихся в данной школе, а  - множество всех учеников из 10 класса. Тогда пересечение
- множество всех учеников из 10 класса. Тогда пересечение  - множество мальчиков, которые учатся в этом классе.
- множество мальчиков, которые учатся в этом классе.
Разностью C двух множеств  называется множество, состоящее из всех элементов
называется множество, состоящее из всех элементов  , не входящих в
, не входящих в  . Обозначают это так:
. Обозначают это так:  . Таким образом, из множества
. Таким образом, из множества  достаточно удалить общие элементы
достаточно удалить общие элементы  , то есть все элементы
, то есть все элементы  , чтобы получить разность
, чтобы получить разность  . На рисунках для разных случаев заштрихованные множества – это разность
. На рисунках для разных случаев заштрихованные множества – это разность  двух множеств.
двух множеств.

Примеры: а) Если  - множество всех учащихся 8 класса данной школы, а
- множество всех учащихся 8 класса данной школы, а  - множество всех девочек, которые учатся в школе, то
- множество всех девочек, которые учатся в школе, то  - множество всех мальчиков, которые обучаются в этом 8 классе.
- множество всех мальчиков, которые обучаются в этом 8 классе.
б) Пусть  – множество натуральных чётных чисел, а
– множество натуральных чётных чисел, а  – множество всех целых чисел, делящихся на 4. Тогда
– множество всех целых чисел, делящихся на 4. Тогда  – множество всех чётных натуральных чисел, которые не делятся на 4.
– множество всех чётных натуральных чисел, которые не делятся на 4.
в) Разность множества чётных чисел и множества целых чисел является пустое множество.
4. Основные законы операций над множествами.
1.  переместительные законы объединения и пересечения множеств.
переместительные законы объединения и пересечения множеств.
2.  сочетательные законы объединения и пересечения множеств.
сочетательные законы объединения и пересечения множеств.
3.  . Здесь роль пустого множества аналогична роли числа 0 в алгебре. Однако свойство
. Здесь роль пустого множества аналогична роли числа 0 в алгебре. Однако свойство  уже не имеет аналога в алгебре.
уже не имеет аналога в алгебре.
4.  .
.
5.  распределительный закон пересечения относительно объединения;
распределительный закон пересечения относительно объединения;  распределительный закон объединения относительно пересечения.
распределительный закон объединения относительно пересечения.
Задание для самостоятельной работы.
Вариант 1.
Дано:  .
.
Найти:  ;
;  ;
;  .
.
Построить диаграммы Венна.
Вариант 2.
Дано:  .
.
Найти:  ;
;  ;
;  .
.
Построить диаграммы Венна.
3. Содержание отчёта.
3.1 Название работы.
3.2 Выполнение работы.
Литература
Основная
1.Пехлецкий И.Д. Математика: 2018 ОИЦ «Академия».
Дополнительные источники:
2. Григорьев С.Г., Задулина С.В. Математика: 2010 ОИЦ «Академия».
3.Омельченко В.П., Математика: учебное пособие/ Омельченко В.П., Курбатова Э.В. – Ростов н/Д.: Феникс, 2005
4.Богомолов Н.В. «Практические занятия по высшей математике», - М., Высшая школа, 1999
5. Подольский В.А. и др. Сборник задач по математике для техникумов. – М.: Высшая школа, 1999
6.Валуцэ И.И. и др. Математика для техникумов на базе средней школы: учебное пособие – М.: Наука, 1990
7. Дадаян А.А. Математика: учеб. – М.: ФОРУМ: ИНФРА – М, 2005
8.Математика для техникумов. Алгебра и начала анализа: в 2-х частях, учеб./Каченовский М.И. и др. под ред. Г.Н. Яковлева, - М.: Наука, 1987
9.Высшая математика для экономистов. Под ред. Н.Ш.Кремера. – М.: ЮНИТИ, 2007
10.Спирина М.С. Дискретная математика: учеб. – М. Академия, 2006.
11.Гончарова Г.А., Мочалин А.А. Элементы дискретной математики: учебное пособие – М.: Форму: ИНФРА-М, 2003
12. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике: учебное пособие – М.: Высшая школа, 1998
13. Гмурман В.Е. Теория вероятностей и математическая статистика. Москва «Высшая школа» 1998
Интернет-ресурсы:
http: //www.alleng ru /edu/
http: //www.metod-kopilka.ru/
http: //www.klyaksa.net/
РЕЦЕНЗИЯ
на методические указания
по выполнению практических занятий
по дисциплине Математика
(Наименование)
для специальности 38.02.01 Экономика и бухгалтерский учет (по отраслям).
( Код, наименование)
разработчик Ромащенко Т.А.
(Ф.И.О.)
На рецензию представлено учебно-методическое пособие «Методические указания по выполнению практических занятий по дисциплине «Математика». Учебно-методическое пособие предназначено для студентов 2 курса СПО. Методические указания составлены в соответствии с ФГОС среднего (полного) общего образования в пределах основных образовательных программ СПО, с учетом профиля специальности.
Представленные на рецензию методические указания включают в себя предисловие, содержание методических указаний, требования к знаниям и умениям при выполнении ПЗ, 17 практических занятий, соответствующих темам рабочей программы по дисциплине «Математика» и перечень литературы.
В учебно-методическом пособии раскрыты методики выполнения всех практических занятий. По каждому занятию определено: тема, цель работы; дано задание и теоретический минимум (в форме методических указаний), необходимый для выполнения заданий.
Данные методические указания позволяют не только формировать умения применять полученные знания на практике, но и развивать такие профессионально значимые качества, как самостоятельность, ответственность, точность, творческая инициатива.
Заключение: данные методические указания рекомендуются к использованию при подготовке квалифицированных специалистов среднего звена.
Рецензент: Калашников Г.И.
(фамилия, имя, отчество)
преподаватель ГБПОУ РО «САТК»
(место работы, должность, образование)
Подпись _______________ Дата __________ Телефон _______________