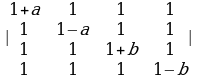2.Минор жана алгебралык толуктоочу
Аныктама: n-тартиптүү аныктагычтын кандайдыр бир aij элементи боюнча минору деп –бул элемент жайгашкан турган i-жолчону жана j-мамычаны өчүрүүдөн жаралган n-1 тартиптүү аныктагыч аталат жана Mij деп белгиленет
Мисалы, 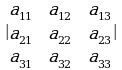 аныктагыч үчүн а22 элементи турган жолчону жана мамычаны өчүрүүдөн:
аныктагыч үчүн а22 элементи турган жолчону жана мамычаны өчүрүүдөн: 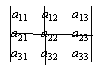 жаралган минор:
жаралган минор: 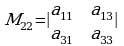 .
.
Аныктама: Аныктагычтын кандайдыр бир aij элементи боюнча i+j сумма жуп сан болгондо Mij миноруна барабар, i+j сумма так сан болгондо Mij минорунан белгиси менен айрымаланган аныктагыч алгебралык толуктоочу деп аталат жана Аij деп белгиленет:
Аij =(-1)i+j Mij
Мисал. 1)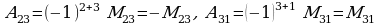
2) Төмөнкү матрицанын бардык элементтеринин алгебралык толуктоочторун тапкыла:
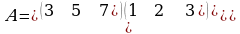
Чыгаруу:
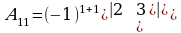
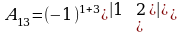
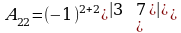
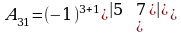
3.Аныктагычты кандай бир катардын
элементтери боюнча ажыратуу
Лапластын теоремасы: Берилген n-тартиптеги 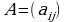 матрицанын аныктагычы det А, ал матицанын каалаган жодчосунун (же мамычасынын) ар бир элементин анын алгебралык толуктоочуна көбөйтүп, ал көбөйтүндүлөрдү кошкондогу суммага барабар, б.а.
матрицанын аныктагычы det А, ал матицанын каалаган жодчосунун (же мамычасынын) ар бир элементин анын алгебралык толуктоочуна көбөйтүп, ал көбөйтүндүлөрдү кошкондогу суммага барабар, б.а.
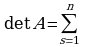
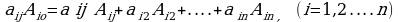 (3)
(3)
Формуланы кеёейтип жаçсак:
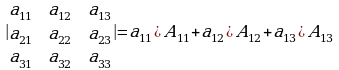 ,
,
б.а.
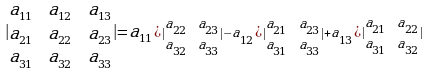
Аныктама. Аныктагычтын кандай бир катары1 боюнча элементтерин ошол элементтер боюнча алгебралык толтуруучуга көбөйтүп, суммасын алуу –аныктагычты кандайдыр бир катардын элементтери боюнча ажыратуу деп аталат жана ал сумма аныктагычтын маанисин берет.
Лапластын теоремасын 3-тартиптеги аныктагычты эсептөөдө колдонуп эсептөөдөн,
(1-жолчонун элементтери менен ажыратып) төмөнкү формула алынат:
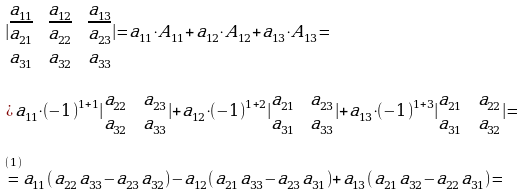
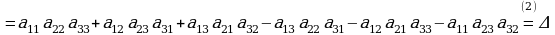
Мындай жол менен үчүнчү тартиптүү аныктагычтын тартибин экинчи тартипке төмөндөттүк, б.а. аны тартиби бир бирдикке төмөндөгөн үч даана аныктагычты эсептөөгө алып келдик. Дал ушул жол менен жогорку тартиптүү аныктагычтарды эсептөө мүмкүнчүлүгү жаралат. Төртүнчү тартиптеги аныктагычты деле ушул жол менен үчүнчү тартиптеги аныктагычтын (минорлордун) жардамы менен эсептесе болот.
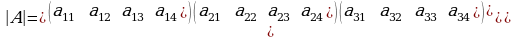 =
=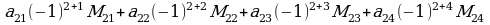
Мында 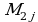 (
(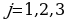 )
) 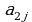 -элементи турган жолчону жана мамычаны чийгенден калган 3- тартиптеги аныктагычтар, б.а.
-элементи турган жолчону жана мамычаны чийгенден калган 3- тартиптеги аныктагычтар, б.а.
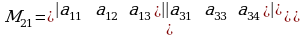 ,
, 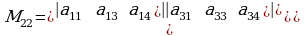 ,
,
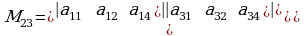 ,
, 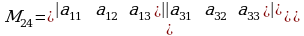
Мисал. Төмөнкү аныктагычты эсептегиле.
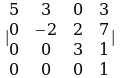
Чыгаруу. Биринчи мамыча боюнча ажыратуудан төмөнкү келип чыгат:
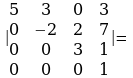 =
=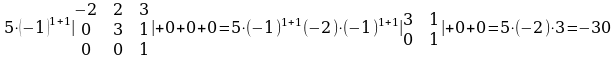

Лапластын теоремасынын негизги мааниси n-тартиптеги аныктагычты эсептөөнү (n-1) – тартиптеги аныктагычтарды эсептөөгө алып келет.
Аныктагычтар төмөнкү касиеттерге ээ:
Келтириген касиеттер каалагандай тартиптеги аныктагычтар үчүн орундуу жана алардын далилдөөсү түçдөн-түç анктамадан келип чыгат.
1. Эгерде квадраттык матрицанын кандайдыр бир жолчосунун (же мамычасынын) бардык элементтери нөл болсо, анда ал матрицанын аныктагычы нөлгө барабар.
2. Эгерде матрицанын кандайдыр бир жолчосун (мамычасын) 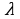 санына көбөйтүүдөн, ал матрицанын аныктагычы
санына көбөйтүүдөн, ал матрицанын аныктагычы 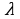 санына көбөйтүлөт, жана тескерисинче: катардын жалпы көбөйтүүчүсүн аныктагычтын белгиси алдына чыгарууга болот:
санына көбөйтүлөт, жана тескерисинче: катардын жалпы көбөйтүүчүсүн аныктагычтын белгиси алдына чыгарууга болот:
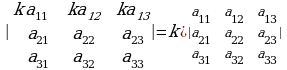
3. Квадраттык А матрицаны транспозициялоодон, ал матрицанын аныктагычы өзгөрбөйт б.а. det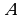 =det
=det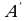 , мында
, мында 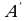 - транспозицияланган матрица. Жекече алганда:
- транспозицияланган матрица. Жекече алганда:
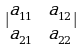 =
=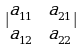 жана
жана 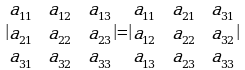 .
.
Демек, аныктагычтын жолчолору жана мамычалары бирдей укукта –мааниде болгондуктан, мындан ары касиеттерди келтирүүдө аларды жалпысынан катар деп айтып өтөбүç.
4. Квадраттык матрицанын эки жолчосунун (же эки мамычасынын) ордун алмаштыруудан, анын аныктагычы белгисин карама – каршы белгиге өзгөртөт, абсолюттук мааниси сакталат. Жекече алганда:
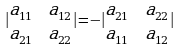
5. Эгерде квадраттык матрица бирдей эки жолчону (же эки мамычаны) камтыса, анда ал матрицанын аныктагычы нөлгө барабар.
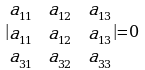
6. Эгерде матрицанын эки жолчосу (же эки мамычасы) пропорционалдуу болсо, анда ал матрицанын аныктагычы нөлгө барабар.
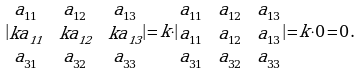
7. Квадраттык матрицанын кандайдыр бир жолчосунун (мамычасынын) ар бир элементин башка жолчонун (мамычанын) элементинин алгебралык толуктоочуна көбөйтүп, ал көбөйтүндүлөрдү кошкондогу сумма нөлгө барабар, б. а.
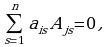
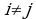 же
же 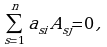
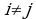
8. квадраттык матрицанын кандайдыр бир жолчосуна (мамычасына), каалаган санга көбөйтүлгөн башка жолчонун (мамычанын) элементтерин кошуудан, ал матрицанын аныктагычы өзгөрбөйт.
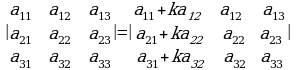
9. Квадраттык матрицанын кандайдыр бир жолчосунун (мамычасынын) элементтеринин алгебралык толуктоочторун каалаган 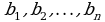 сандары менен алмаштыргандагы матрицанын аныктагычына барабар.
сандары менен алмаштыргандагы матрицанын аныктагычына барабар.
10. Эки квадраттык матрицанын көбөйтүндүсүнүн аныктагычы ал матрицалардын аныктагычтарынын көбөйтүндүсүнө барабар, б.а. 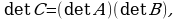 мында
мында 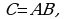
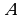 жана
жана 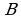 -
-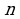 - тартиптеги матрицалар.
- тартиптеги матрицалар.
11. Аныктагычтын кандайдыр бир катарынын элементтери эки кошулуучунун суммасынан турса, анда аныктагыч тиешелүү эки аныктагычтын суммасына ажырайт:
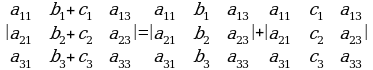
12. Аныктагычтын кандайдыр бир катарынын элементтеринин жарыш катардагы тиешелүү алгебралык толуктоочуларга көбөйтмөсүнүн суммасы нөлгө барабар.
Мисалы, 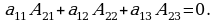
Бышыктоо үчүн көнүгүүлөр
1.Эсептегиле: а)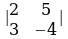 , б)
, б)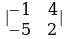 , в)
, в)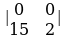 , г)
, г)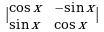 .
.
2./ч бурчтук эрежеси боюнча эсептегиле:
а)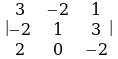 , б)
, б) 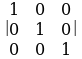 , в)
, в)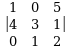 , г)
, г)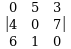 .
.
3. 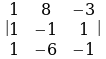 аныктагычтын биринчи жолчосу боюнча минорлорду жана алгебралык толуктоочуларды тапкыла.
аныктагычтын биринчи жолчосу боюнча минорлорду жана алгебралык толуктоочуларды тапкыла.
4. /чүнчү жолчонун элементтери боюнча ажыратуу менен аныктагычты эсептегиле:
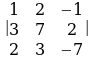
5. Жолчолордун (мамычалардын) сызыктуу комбинациясы теоремасынан пайдаланып аныктагычты эсептегиле: 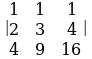
6. Эсептегиле: 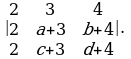
7.Эсептегиле.
а)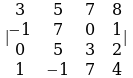 , б)
, б)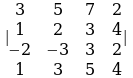 , в)
, в)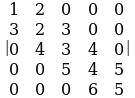 , г)
, г)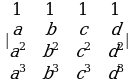
8. Тартибин төмөндөтүү менен аныктагычтарды эсептегиле.
а)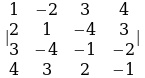 , б)
, б)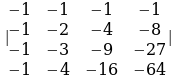 , в)
, в)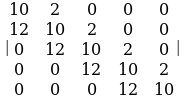 , г)
, г)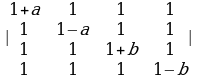
1� Мында аныктагычтын кандайдыр бир жолчосу же мамычасы түшүнүлөт.






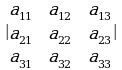 аныктагыч үчүн а22 элементи турган жолчону жана мамычаны өчүрүүдөн:
аныктагыч үчүн а22 элементи турган жолчону жана мамычаны өчүрүүдөн: 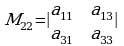 .
.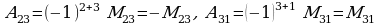
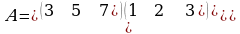
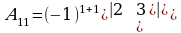
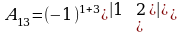
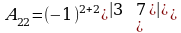
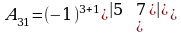
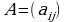 матрицанын аныктагычы det А, ал матицанын каалаган жодчосунун (же мамычасынын) ар бир элементин анын алгебралык толуктоочуна көбөйтүп, ал көбөйтүндүлөрдү кошкондогу суммага барабар, б.а.
матрицанын аныктагычы det А, ал матицанын каалаган жодчосунун (же мамычасынын) ар бир элементин анын алгебралык толуктоочуна көбөйтүп, ал көбөйтүндүлөрдү кошкондогу суммага барабар, б.а.
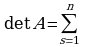
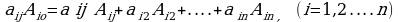 (3)
(3)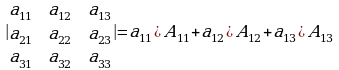 ,
,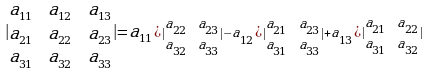
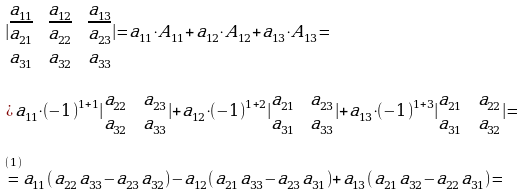
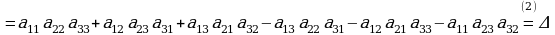
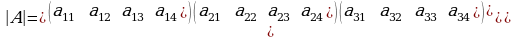 =
=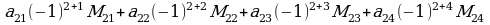
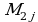 (
(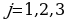 )
) 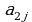 -элементи турган жолчону жана мамычаны чийгенден калган 3- тартиптеги аныктагычтар, б.а.
-элементи турган жолчону жана мамычаны чийгенден калган 3- тартиптеги аныктагычтар, б.а.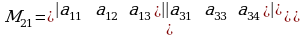 ,
, 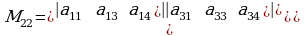 ,
, 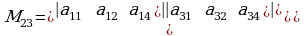 ,
, 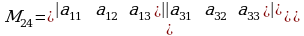
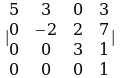
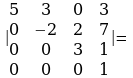 =
=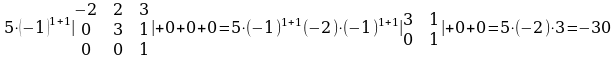
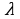 санына көбөйтүүдөн, ал матрицанын аныктагычы
санына көбөйтүүдөн, ал матрицанын аныктагычы 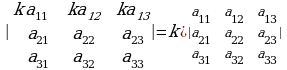
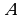 =det
=det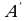 , мында
, мында 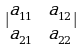 =
=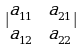 жана
жана 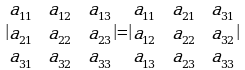 .
.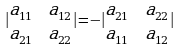
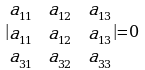
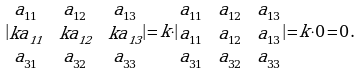
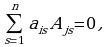
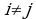 же
же 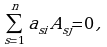
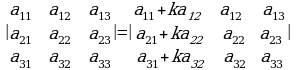
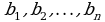 сандары менен алмаштыргандагы матрицанын аныктагычына барабар.
сандары менен алмаштыргандагы матрицанын аныктагычына барабар.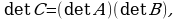 мында
мында 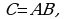
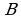 -
-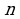 - тартиптеги матрицалар.
- тартиптеги матрицалар.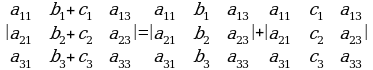
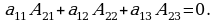
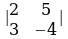 , б)
, б)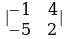 , в)
, в)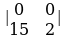 , г)
, г)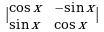 .
.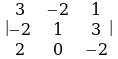 , б)
, б) 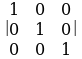 , в)
, в)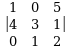 , г)
, г)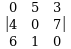 .
.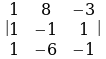 аныктагычтын биринчи жолчосу боюнча минорлорду жана алгебралык толуктоочуларды тапкыла.
аныктагычтын биринчи жолчосу боюнча минорлорду жана алгебралык толуктоочуларды тапкыла.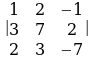
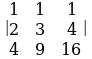
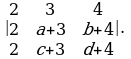
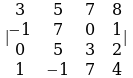 , б)
, б)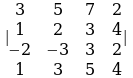 , в)
, в)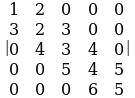 , г)
, г)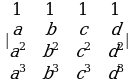
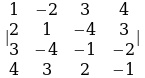 , б)
, б)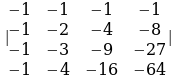 , в)
, в)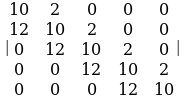 , г)
, г)