Наглядность и моделирование в обучении математике
В процессе жизни у ребенка последовательно формируется три вида мышления:
—наглядно-действенное;
—наглядно-образное;
—абстрактно- теоретическое (понятийное).
В процессе обучения все три вида мышления развиваются в тесном взаимодействии друг с другом. ИЛ. Павлов убедительно показал, что словесно-знаковое требует постоянного подкрепления со стороны образного, а образное, в свою очередь, требует активной деятельности органов чувств. Как указывает Н.А. Менчинская. это взаимодействие наглядного и абстрактного мышления начинается с мысленного образования наглядных образцов на основе словесного текста, в форме перевода на язык образов содержания, описанного в словах.
Это взаимодействие наглядного и понятийного мышления связано с тем, что последнее невозможно без первого. «Мы не можем, - писал И.Кант, - мыслить линии, не проведя ее мысленно, не можем мыслить окружность, не описывая ее, не можем представить себе три измерения, не проведя из одной точки трех перпендикулярных, друг к другу линий».
Учитывая эту особенность мышления человека, еще с времен Я.А. Коменского, одним из основных принципов обучения считается принцип наглядности.
Исследования же психологов последних лет показали, что такое понимание принципа наглядности является примитивным и не соответствует закономерностям детского мышления.
А.Н. Леонтьев указывает, что наглядный материал должен служить ОПОРОЙ для аналитической деятельности учащихся. Если наглядный материал не является внешней опорой для внутренней работы мысли, то он бесполезен! Поэтому, особенно в курсе математике основным является не принцип наглядности, а принцип моделирования.
В чем состоит принцип моделирования?
Принцип моделирования не противопоставляется принципу наглядности - он лишь является его высшей ступенью, его развитием и обобщением.
Моделирование в обучении математике необходимо для формирования научно-теоретического стиля мышления. Что изменится от того, что учащиеся узнают, что например, уравнение, полученное в ходе решения текстовой задачи, есть математическая модель этой задачи? Или у=кх - это есть математическая модель физических, химических и других явлений как S=vt, F=ma, С=2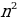 , и т.д.
, и т.д.
Долгое время традиционная система образования была озадачена тем, чтобы дать учащимся определенную систему знаний.
В каждой отрасли науки накоплена теперь такая масса знаний, что все это возможно вложить в голову одного человека, как долго бы он не обучался. Человек мечется в хаосе случайных ассоциаций, пытаясь установить связи между отдельными фактами. Вихрь сведений крутит его, волнует его, вызывает рост и без того высокой тревожности. От обилия разнообразных, беспорядочных сведений в памяти остается мимолетное представление.
Как же часто причину удач или неудач в познании относят за счет природных данных, а не за счет методик технологий.
Рассмотрим одну из методических рекомендаций: моделирование - это способ кодирования информации нервной системой.
Известный психолог Дж. Бунер в книге «Психология познания» писал: «Организм усваивает (кодирует) объекты...». Кодирует - усваивает. Мысленные операции над информацией мозг осуществляет в тех или иных конкретных кодах. Никто из нас не держит в голове полных текстов изученных нами книг, но в голове остается своего рода схема, код или сеть опорных узлов, по которым мы можем восстановить текст. И, следовательно, качество и прочность наших знаний полностью зависят от качества и прочности содержащихся в памяти кодов. У одних они точные, ясные и полные, у других искаженные, отрывочные и туманные. Этим собственно и отличается знающий человек от незнающего или мало знающего.
Как бы небыли хороши учебник и рассказ учителя, в голове ученика остается тот код, та схема, которую он САМ составил, и ничего больше. Но почему САМ? Почему труднейшую умственную работу, от которой зависит успех учения, мы перекладываем на ученика?
Для схемы, для знаковой модели школьнику необходимо выделить главное. Но что такое главное, как - отличить его от второстепенного. Задача трудна не только для школьника. Например,
Тема: «Квадратные уравнения».
Учителю необходимо выделить, что необходимо знать и что надо уметь.
Что знать:
Определение квадратного уравнения;
Вывод общей формулы корней квадратного уравнения;
Исследование квадратного уравнения по дискриминанту;
Виды неполных квадратных уравнений и уравнений, приводимых к квадратным.
Уметь:
Привести любое уравнение к нормальному виду и определить является ли оно квадратным;
Выделить полный квадрат;
Решать любые квадратные уравнения;
Определять знаки корней по теореме Виета;
Составлять квадратное уравнение по его корням;
Решать задачи по теме.
Обзорная лекция по теме, отражающей материал нескольких тем:
«Квадратные уравнения»;
«Квадратный трехчлен»;
«Квадратная функция»;
«Квадратные неравенства».
УДЕ - укрупненная дидактическая единица с первого же урока дает возможность учащимся:
—осознать конечную цель — знать формулу корней квадратного уравнения, ее взаимосвязь со всеми четырьмя темами;
—увидеть закономерности в ходе дальнейшего изучения;
—охватить мысленным взором весь объем, познавательной деятельности;
—выделить главные, узловые моменты темы, не останавливаясь на второстепенном;
—развивать зрительную, слуховую, двигательную, эмоциональную, ассоциативную. .памяти;
—осуществлять взаимосвязь нового с ранее изученным;
—развивать гибкость мышления;
—развивать готовность памяти вспомнить нужное в нужный момент;
—осуществлять принцип многократности повторения, т.е. осуществлять как повторение, так и опережение.
Кроме всего, помогаю эти приёмы т осуществить экономию времени, повысить информативную емкость урок.
Четкое, ясное сжатое символическое обозначение основного облегчает усвоение информации.
Экономная запись уже известных фактов, лаконичная форма изложения уже усвоенной теории - это предпосылка продвижения вперед.
Ввести удобный способ занятий, кратко и красиво изложить уже известное - такая работа тоже носит творческий характер и требует нестандартного мышления.
Теория П.Я. Гальперина о поэтапном формировании умственных действий это учение о сложных многоплановых изменениях, связанных с образованием у человека новых действий, образцов понятий.
Понятие ООД (ориентировочной основы действий) введено П.Я. Гальпериным и развито Н.Ф. Талызиной. Чтобы учащиеся смогли освоить ООД, сделать это можно путем моделирования, путем составления схем графиков, блоков и т.п. Этому конечно необходимо учащихся обучать. Но на первых порах им даются готовые схемы, таблицы, знаковые модели.
Если рассмотреть по теме «Прямоугольный треугольник», то можно отметить, учащимся предоставлена возможность в сжатой лаконичной форме увидеть все свойства прямоугольного треугольника, как общие (сумма внутренних углов, периметр, площадь и т.д.) так и его специфические свойства:
—свойство острых углов;
—особенность свойств, когда острый угол содержит 30°;
—теорема Пифагора;
—как возникли определения Sin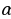 ,Co
,Co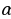 ,Tg
,Tg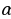 ,Ctg
,Ctg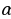 острых углов и т.д.
острых углов и т.д.
Именно целостное восприятие всех его свойств дает возможность
увеличить объем кратковременной памяти, готовность памяти вспомнить именно ту формулу, которая является наиболее рациональной в данном случае: например, нахождение катета: a=c*SinL; a=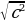 -
- 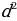 ; a=
; a=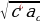 ; использовать примеры сравнения и сопоставления (среднее геометрическое и среднее арифметическое) в задачах на построение, увидеть теорему Пифагора в задачах на построение графика типа x=
; использовать примеры сравнения и сопоставления (среднее геометрическое и среднее арифметическое) в задачах на построение, увидеть теорему Пифагора в задачах на построение графика типа x=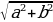 ; х= x=
; х= x=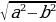 и др.
и др.
Кроме того, в любых явлениях жизни необходимо находить закономерности:
—нахождение острого угла по известному другому острому углу;
—увидеть что Sin 30° =Cos 60° и догадываться, что
Sin 10° =Cos 80°
—увидеть закономерность для углов 30°, 45°, 60°; 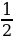 ;
;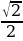 ;
;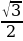 , ЧТО знаменатель везде «2» а числитель
, ЧТО знаменатель везде «2» а числитель 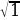 ,
,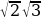 , и т.д.
, и т.д.
Данная информация необходима не только учащимся 8х классов. В курсе 9-11 классов она поможет формированию такой творческой способности, как «сцепление» и перенос знаний. Способность объединять вновь воспринятые
сведения с тем, что было известно ранее, включать их в уже имеющиеся системы знаний, является предпосылкой другой чрезвычайно важной способности к переносу. Это, по сути, способность к нахождению аналогий, к выработке обобщающих строений которые могут быть применены при решении широкого круга проблем.
Способность к переносу настолько важна, что развитие ее нельзя предоставлять воле случая. Если новые сведения не увязываются с прежними знаниями, то восприятие новой информации не превращается в знание, не становится частью интеллекта, а остается мертвым грузом.
Зубрежка заменится пониманием теоретических положений. А развитие речи и мышления происходит одновременно. Еще никогда и никому не удавалось размышлять, не облекая свои мысли в слова и фразы. Мышление и речь (внутренняя или внешняя) — единый процесс. Но не секрет, если дети страдают дефектами речи, застенчивые от природы или отстающие от своих товарищей по какой - либо причине, неделями не произносят на уроках ни одного слова. Они боятся говорить, а у нас нет времени ждать, пока он выскажется. Данное построение урока снимает страх, экономит время, что повышает информационную ёмкость урока.





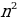 , и т.д.
, и т.д.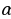 ,Co
,Co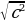 -
- 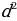 ; a=
; a=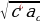 ; использовать примеры сравнения и сопоставления (среднее геометрическое и среднее арифметическое) в задачах на построение, увидеть теорему Пифагора в задачах на построение графика типа x=
; использовать примеры сравнения и сопоставления (среднее геометрическое и среднее арифметическое) в задачах на построение, увидеть теорему Пифагора в задачах на построение графика типа x=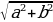 ; х= x=
; х= x=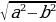 и др.
и др.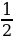 ;
;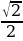 ;
;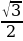 , ЧТО знаменатель везде «2» а числитель
, ЧТО знаменатель везде «2» а числитель 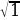 ,
,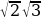 , и т.д.
, и т.д.









