| План урока | Деятельность учителя | Записи на доске | Деятельность учащихся | Записи в тетради |
| Орг. момент Мотивация
2 мин | - Здравствуйте, ребята! Запишите число и тему урока. - Скажите, известны ли вам понятия «наибольшее и наименьшее значение функции»? Так в чем же смысл этого урока? И зачем уточнения в теме урока о непрерывности функции, и решении задач на промежутке? Надеюсь, к концу урока вы найдете ответы на эти вопросы. | Тема урока «Нахождение наибольшего и наименьшего значений непрерывной функции на промежутке»
| - Здравствуйте!
- Да, известны, ранее мы изучали, что называют «наибольшим и наименьшим значением функции» | Записывают дату и тему урока. |
| Актуализация знаний. Уточнение смысла понятия «наибольшее и наименьшее значение функции»
5 мин.
| Посмотрите на рисунок. Перед вами график функции «Суточный цикл активности мозга». Ответьте на вопросы по данному графику. Если утверждение верно, то поставьте число 1, неверно 0.
Проверьте себя, правильное число 11001 | 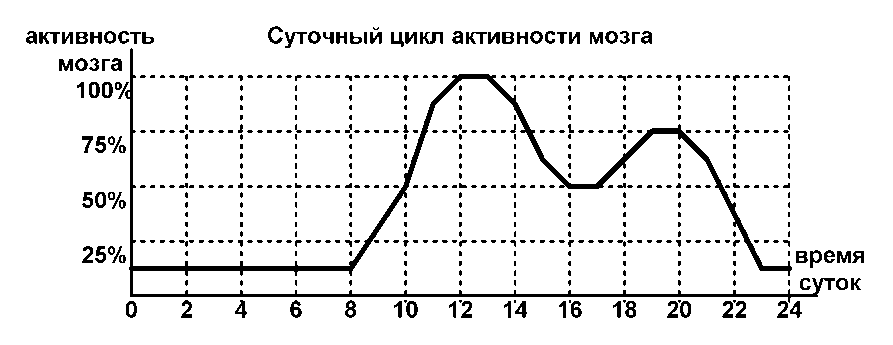
1.Область определения функции – это отрезок от 0 до 24 часов. 2. Значение функции в минимуме равно 50%. 3. Наибольшие значения функции равны 100% и 75%. 4. Наименьшее значение функции с 9 до 18 часов равно 50%. 5. С 16 до 17 часов наименее продуктивное время для выполнения домашнего задания. | Отвечают на вопросы. | Записывают ответы на вопросы |
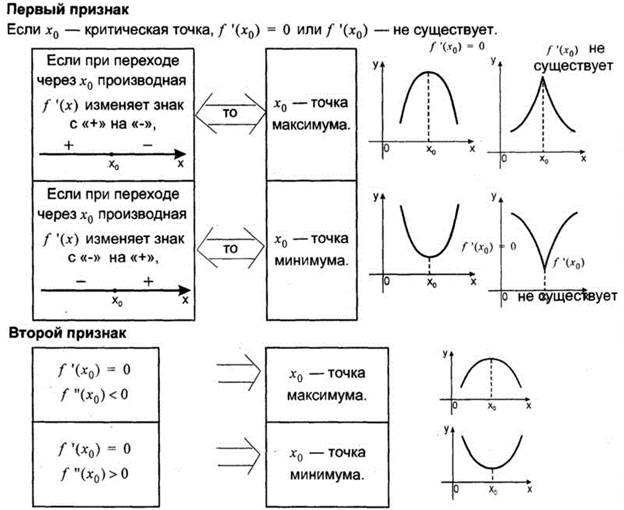
| - Напомните, что называют наибольшим и наименьшим значением функции? - Как принято обозначать наибольшее и наименьшее значением функции? - В чем разница между экстремумами и наибольшим (наименьшим) значением функции?
В помощь вам рисунки на доске.
-В чем разница между заданиями: «Найдите точку максимума (минимума)», «Найдите значение функции в максимуме (минимуме)», «Найдите наибольшее (наименьшее) значение функции». | В чем разница между экстремумами и наибольшим (наименьшим) значением функции? 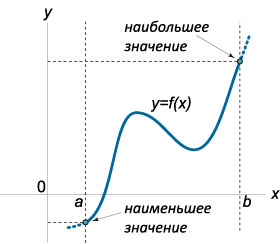 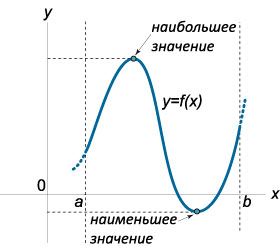
 
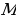
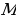

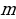

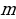
Число m называют наименьшим значением функции на множестве X, если во множестве Х существует точка 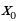 , такая, что f( , такая, что f(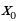 )=m и f(x)≥m для всех значений х из множества Х. )=m и f(x)≥m для всех значений х из множества Х.
Число M называют наибольшим значением функции на множестве X, если во множестве Х существует точка 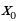 , такая, что f( , такая, что f(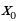 )=M и f(x)≤M для всех значений х из множества Х. )=M и f(x)≤M для всех значений х из множества Х.
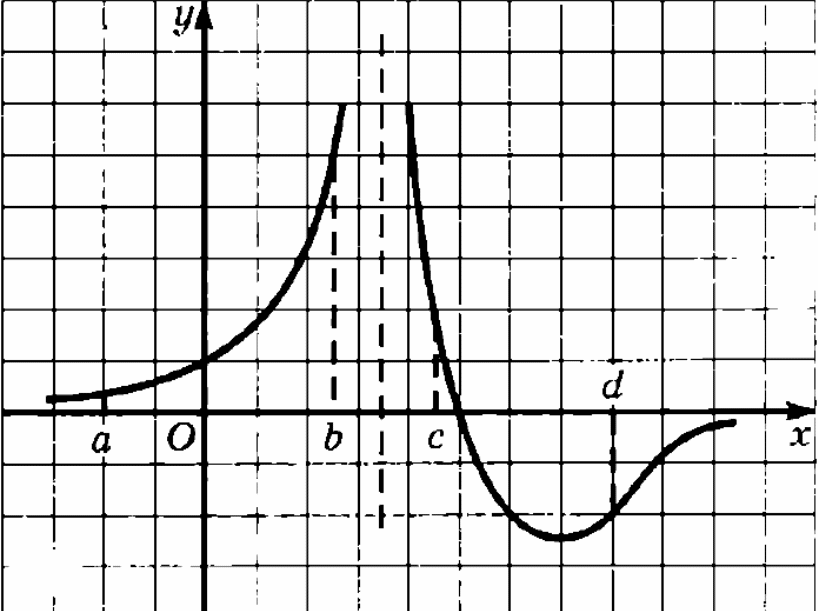
| -Наибольшее (наименьшее) значение функции – самая большая (маленькая) ордината функции на заданном множестве. - Наибольшее и наименьшее значением функции принято обозначать 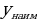 и и 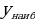 . . - Наибольшее и наименьшее значения функции не обязательно совпадают со значением функции в экстремумах!
- «Найдите точку максимума (минимума)» значит определить абсциссу в которой функция имеет максимум (минимум). «Найдите значение функции в максимуме (минимуме)» определить чему равна ордината, в которой функция имеет максимум (минимум), «Найдите наибольшее (наименьшее) значение функции» - это всегда определить ординату. |
|
| Выявление условий существования наибольшего (наименьшего) значения функции
5 мин | - Подумайте, чем являются точки в которых функция достигает наибольшего (наименьшего) значения? Всегда ли можно определить наибольшее (наименьшее) значение функции? По графику функции заполните таблицу, распечатанную на «листочках», и сделайте вывод о точках, в которых функция достигает наибольшего (наименьшего) значения.
Ответьте на вопросы опираясь на полученные результаты в таблице.
-Всегда ли функция имеет наибольшее (наименьшее) значения на отрезке?
- Всегда ли непрерывная функция имеет наибольшее (наименьшее) значения на отрезке?
- Действительно, в подтверждение данных выводов запишем теорему: (Теорема Вейерштрасса) если функция определена и непрерывна на отрезке, то она имеет наибольшее и наименьшее значение на этом отрезке. Эта весьма солидная теорема курса математического анализа, доказательство ее требует достаточной продвинутости в изучении курса, поэтому примем ее без доказательства. Задача нахождения наибольшего (наименьшего) значения непрерывной функции на отрезке всегда имеет решение, а так как многие прикладные задачи сводятся к нахождению наибольших (наименьших) значений функций, заданных на отрезке, то в дальнейшем мы ограничимся решением задач поиска наибольшего (наименьшего) значения непрерывной функции на всей области определения или отрезке. | Всегда ли функция имеет наибольшее (наименьшее) значение и в каких точках функция может достигать наибольшего (наименьшего) значения?
| на отрезке | на интервале | | 1 | [a;b] | 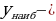
|
| 4 | (-∞;+∞) | 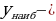
|
| | 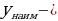
|
| 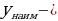
|
| | 2 | [c;d] | 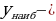
|
| 5 | (c; +∞) | 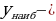
|
| | 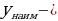
|
| 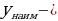
|
| | 3 | [b;c] | 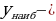
|
| 6 | (a;b) | 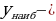
|
| | 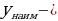
|
| 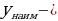
|
| | Вывод: | Вывод: |
| Заполняют таблицу: | на отрезке | | 1 | [a;b] | 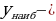 на конце отрезка на конце отрезка
| | 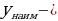 на конце отрезка на конце отрезка
| | 2 | [c;d] | 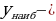 на конце отрезка на конце отрезка
| | 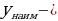 в минимуме в минимуме
| | 3 | [b;c] | 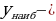 не существует не существует
| | 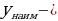 на конце отрезка на конце отрезка
|
| на интервале | | 4 | (-∞;+∞) | 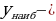 не существует не существует
| | 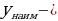 в минимуме в минимуме
| | 5 | (c; +∞) | 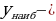 не существует не существует
| | 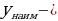 в минимуме в минимуме
| | 6 | (a;b) | 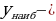 не существует не существует
| | 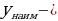 не существует не существует
|
- Если функция имеет наибольшее (наименьшее) значения, то оно достигается либо в точках экстремума, либо на концах отрезка.
- Задача отыскания наибольшего (наименьшего) значения функции не всегда имеет решение. Пример, в таблице 3, 4, 5, 6.
- Нет, пример 3 таблицы.
- Да, если судить по результатам полученным в таблице, пример 1, 2.
|
Вывод1: Если функция имеет наибольшее (наименьшее) значения, то оно достигается либо в точках экстремума, либо на концах отрезка. Вывод 2: Задача отыскания наибольшего (наименьшего) значения функции не всегда имеет решение
Вывод 3: (Теорема Вейерштрасса) Если функция определена и непрерывна на отрезке, то она имеет наибольшее и наименьшее значение на этом отрезке.
|
| Обобщение способов нахождения наибольшего и наименьшего значения функции
10 мин | - Подумайте, можно ли вывести правила нахождения наибольшего и наименьшего значения функции, если необходимо схематично изобразите указанные случаи и сделайте вывод: как определить (наибольшее) наименьшее значение монотонной функции; как определить наибольшее значение немонотонной функции; как определить наименьшее значение немонотонной функции; как определить наибольшее (наименьшее) значение функции, имеющих один экстремум?
- Подумайте, нужно ли находить область определения функции, решая задачи на поиск наибольшего (наименьшего) значения непрерывной функции на отрезке? | Правила нахождения наименьшего и наибольшего значений непрерывной функции y=f(x) на отрезке [a;b]
1.Как определить (наибольшее) наименьшее значение монотонной функции? 2.Как определить наибольшее значение немонотонной функции? 3.Как определить наименьшее значение немонотонной функции? 4.Как определить наибольшее (наименьшее) значение функции, у которых один экстремум? | Работают в тетради, отвечают на вопросы, формулируют правила. - 1. Чтобы определить (наибольшее) наименьшее значение монотонной функции необходимо найти и сравнить значения функции на концах отрезка f(a), f(b). Если известно, что функция возрастает, то наименьшее значение функции равно f(a), наибольшее значение функции равно f(b) и, наоборот, если функция убывает. - 2. Чтобы определить наибольшее значение немонотонной функции, необходимо найти значения функции в максимумах f(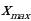 ) и на концах отрезка f(a), f(b). Сравнить полученные ординаты, выбрать наибольшее число. ) и на концах отрезка f(a), f(b). Сравнить полученные ординаты, выбрать наибольшее число. - 3. Чтобы определить наименьшее значение немонотонной функции, необходимо найти значения функции в минимумах f(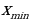 ) и на концах отрезка f(a), f(b). Сравнить полученные ординаты, выбрать наименьшее число. ) и на концах отрезка f(a), f(b). Сравнить полученные ординаты, выбрать наименьшее число. - 4. Если функция имеет один экстремум, то наибольшее значение функции будет равно значению функции в максимуме f(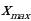 ), соответственно наименьшее значение функции будет равно значению функции в минимуме f( ), соответственно наименьшее значение функции будет равно значению функции в минимуме f(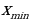 ). ). - 5. Находим область определения функции и проверяем, содержится ли в ней весь отрезок [a;b], а так же нет ли разрыва функции на отрезке. | Правила нахождения наименьшего и наибольшего значений непрерывной функции y=f(x) на отрезке [a;b]: Записывают правила 1-5 под диктовку в тетрадь.
|
| - Мы вспомнили, как находить наибольшее (наименьшее) значение функции по графику, но всегда ли оправданно построение графика функции? Существует ли аналитическое решение данного типа задач. Значение функции на концах отрезка легко вычислить, а можно ли аналитически найти экстремумы функции?
Подумайте и подберите рациональный способ решения задач а) - д) и ответьте на вопросы. | Определите наибольшее и наименьшее значение функций на заданных промежутках (интервалах): а) y=cos x , [0;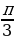 ]; ]; б) y=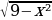 , на всей области определения; , на всей области определения; в) 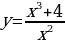 , [1;4], [-4;-1] , [1;4], [-4;-1] г) y=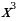 -6 -6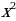 +9x+17, [2;5] (Вариант ЕГЭ 2011) +9x+17, [2;5] (Вариант ЕГЭ 2011) д) y=33x-30sinx+29 ,наибольшее значение на отрезке [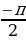 ;0] (Досрочный вариант ЕГЭ 2015) ;0] (Досрочный вариант ЕГЭ 2015)
Решение: а) известно, что косинусоида монотонно убывает на отрезке [0;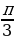 ], поэтому ], поэтому 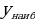 = = 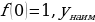 = =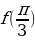 = =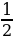 ; ; б) т. к. выражение 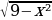 ≥0 и ≥0 и 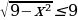 , то , то 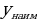 =0 (это значение достигается при х=±3) и =0 (это значение достигается при х=±3) и 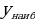 =9 (это значение достигается при х=0). =9 (это значение достигается при х=0).
| Работают у доски и в тетрадях. - В заданиях а), б) очевидны точки, в которых функция достигает наибольшего (наименьшего) значения, поэтому нет необходимости в построении графика функции. В заданиях в), г), д) не ясны не только точки, в которых функция достигает наибольшего (наименьшего) значения, но и сами графики функций. Однако, значение функции на концах отрезка не сложно вычислить, а найти экстремумы можно используя производную функции (Приложение 1).
| Записывают решение а), б) в тетрадь.
Вывод 4: Производная используется в тех случаях, когда графически или «оценкой выражения» отыскать наибольшее и наименьшее значения функции затруднительно.
|
| -Перед вами алгоритм нахождения наименьшего и наибольшего значений непрерывной функции y=f(x) на отрезке [a;b], представленный в учебнике. Проанализируйте алгоритм, подумайте, в каких пунктах вы бы внесли дополнения и уточнения. |  | - Необходимо определить область определения функции. - Необязательно на 3 шаге определять значения функции во всех критических и стационарных точках, нужно отобрать только экстремумы. Если же вопрос задачи в нахождении наибольшего значения функции, то на 2 шаге отбираем только максимумы; при нахождении наименьшего значения функции, отбираем только минимумы. |
|
| Первичное закрепление алгоритма нахождения наибольшего и наименьшего значения функции с помощью производной
10 мин | Записывает решение задания в) на доске.
Задания г) - д), используя алгоритм нахождения наименьшего и наибольшего значений непрерывной функции y=f(x) на отрезке [a;b], выполните самостоятельно, проверьте себя с ответами на доске. | Решение: в) Областью определения функции является все множество действительных чисел, за исключением нуля. Оба отрезка попадают в область определения. Шаг 1.Находим производную функции по правилу дифференцирования дроби:
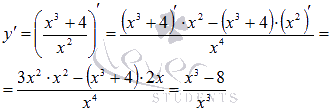 Шаг 2. Очевидно, производная функции не существует при x=0, т.е. существует во всех точках отрезков [1;4] и [-4;-1]. Стационарные точки определим из уравнения 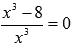 . Единственным действительным корнем является x=2. Эта стационарная точка является минимумом функции и попадает в первый отрезок [1;4]. . Единственным действительным корнем является x=2. Эта стационарная точка является минимумом функции и попадает в первый отрезок [1;4].
Шаг 3. Для первого случая вычисляем значения функции на концах отрезка и в стационарной точке,
4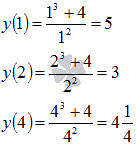 5.Следовательно, 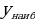 =5, =5, 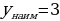 . . Для второго случая вычисляем значения функции лишь на концах отрезка 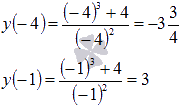 Следовательно, 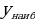 =3, =3, 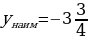 . . | Работают в тетради. | Решение задания в) записывают в тетрадь.
Решение: г) (Шаг1) y'=3x²-12x+9; (Шаг2) y'=0, т.е. x²-4x+3=0 при х=1(не входит в заданный промежуток) или х=3; (Шаг3) y=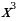 -6 -6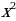 +9x+17 +9x+17 y(2)=19 y(3)=17=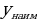 y(5)=37=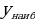 д) (Шаг1) y'=33-30cosx; (Шаг2) y'=0, но 33-30cosx ≠ 0, y'0, т.е. функция монотонно возрастает; (Шаг3) y=33x-30sinx+29 y(0)=29=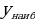
|
| Рефлексия Домашнее задание
5 мин | - Подведем итоги урока. Так в чем же смысл этого урока? Что нового вы узнали на уроке? Выберите наиболее на ваш взгляд подходящий эпиграф к уроку A или B. Выберите из афоризмов 1-5 высказывание наиболее полно отражающее объем знаний полученных на уроке. Помните, что «правильных» вариантов ответа здесь нет.
| A. Приступая к решению любой задачи особенно важно уметь оценивать трудоемкость метода и находить рациональный путь, избегая в некоторых случаях искушения решить задачу универсальным путем. (А.И. Петрова, Е.П. Жиркова, Н.В. Аргунова , С.М. Макарова, В.П. Ефремова) B. Незнающие пусть научатся, знающие – вспомнят еще раз.(Античный афоризм)
-
Как приятно знать, что ты что-то узнал. (Мольер) -
Я знаю только то, что ничего не знаю, но я стремлюсь к знаниям. (Сократ) -
Многие знают больше, чем я. К счастью, меня это не волнует. (Эрпенд Лу) -
Умен тот, кто имеет знание, но делает вид, что не знает. Глуп тот, кто не имеет знания, делает вид, что знает. (Лао Цзы) -
Сомнение и поиск истины доставляет мне не меньшее наслаждение, чем знание. (Данте Алигьери)
| Выполняют самостоятельно задание и сдают учителю. |
|
| Порой вам, кажется, что математика не имеет практического применения. Задумайтесь над проблемами, как располагая определенными ресурсами, добиться наиболее высокого жизненного уровня, наивысшей производительности труда, наименьших потерь, максимальной прибыли и т.д. А это и есть задачи на нахождение наибольшего и наименьшего значения функции. Знакомиться с практическими задачами на поиск наибольшего (наименьшего) значения вы начнете при выполнении домашнего задания. Приемам решения именно таких задач и будет посвящен следующий урок. | Домашнее задание: -
§46, упражнение, 46.16 (задачник), конспект в тетради -
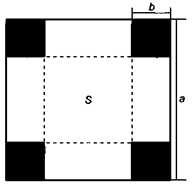
Имеется квадратный лист картона. Из листа по углам вырезают четыре квадрата и склеивают коробку по сторонам вырезов. Какова должна быть сторона вырезаемого квадрата, чтобы коробка имела наибольшую вместимость? (Приложение 2). -
Задача Л. Толстого « Как Пахом покупал землю» Можно ли установить по данным, рассеянным в этом рассказе, сколько примерно десятин земли обошел Пахом? Начертите план обойденного Пахомом земельного участка и определите его площадь. Как должен был идти Пахом, чтобы получить наибольшую площадь земли? Вычислите площадь участка в этом случае. (Приложение 3).
| Знакомятся с домашним заданием на «листочках». |
|
| Орг. момент 1 мин
| Спасибо за активную работу на уроке. До свидания! |
| До свидания! |
|











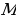

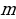
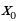 , такая, что f(
, такая, что f(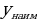 и
и 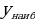 .
.
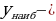
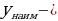
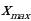 ) и на концах отрезка f(a), f(b). Сравнить полученные ординаты, выбрать наибольшее число.
) и на концах отрезка f(a), f(b). Сравнить полученные ординаты, выбрать наибольшее число.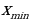 ) и на концах отрезка f(a), f(b). Сравнить полученные ординаты, выбрать наименьшее число.
) и на концах отрезка f(a), f(b). Сравнить полученные ординаты, выбрать наименьшее число.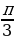 ];
];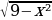 , на всей области определения;
, на всей области определения;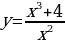 , [1;4], [-4;-1]
, [1;4], [-4;-1]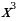 -6
-6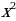 +9x+17, [2;5] (Вариант ЕГЭ 2011)
+9x+17, [2;5] (Вариант ЕГЭ 2011)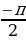 ;0] (Досрочный вариант ЕГЭ 2015)
;0] (Досрочный вариант ЕГЭ 2015)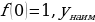 =
=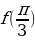 =
=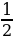 ;
;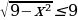 , то
, то 
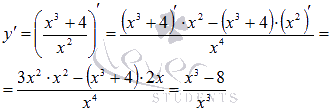
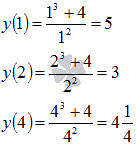
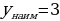 .
.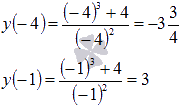
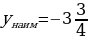 .
.
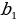 =1
=1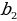 =2
=2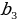 =3
=3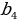 =4
=4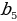 =5
=5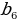 =
=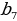 =
=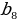 =
=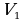 =
=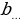 =…
=…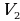 =
=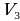 =
=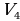 =
=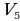 =
=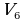 =
=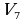 =
=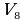 =
=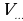 =
=



















