Нахождение расстояния от точки до плоскости с использованием свойства прямой, параллельной плоскости.

Расстояние от точки до плоскости

Задачи на нахождение расстояния от точки до плоскости ( типовые задачи С2)

Подготовила:

учитель математики

МОУ «Гимназия №1»

г. Железногорска Курской области

Агашкова Н.А.

Расстояние от точки до плоскости

4. Нахождение расстояния от точки до плоскости, с использованием свойства прямой, параллельной плоскости.

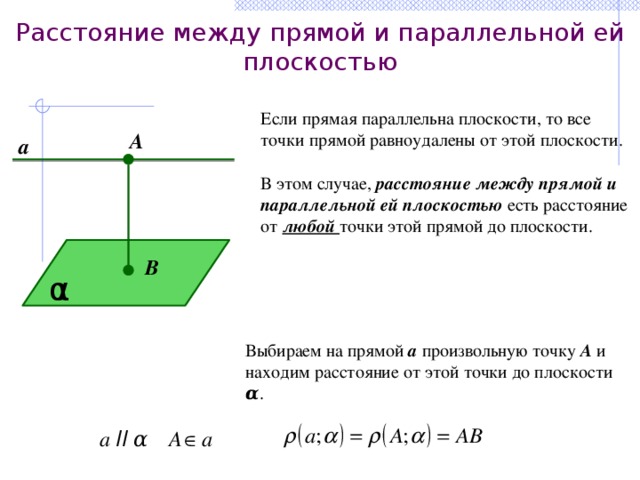
Расстояние между прямой и параллельной ей плоскостью

Если прямая параллельна плоскости, то все точки прямой равноудалены от этой плоскости.

В этом случае, расстояние между прямой и параллельной ей плоскостью есть расстояние от любой точки этой прямой до плоскости.

A

а

B

α

Выбираем на прямой а произвольную точку А и находим расстояние от этой точки до плоскости α .

a ІІ α

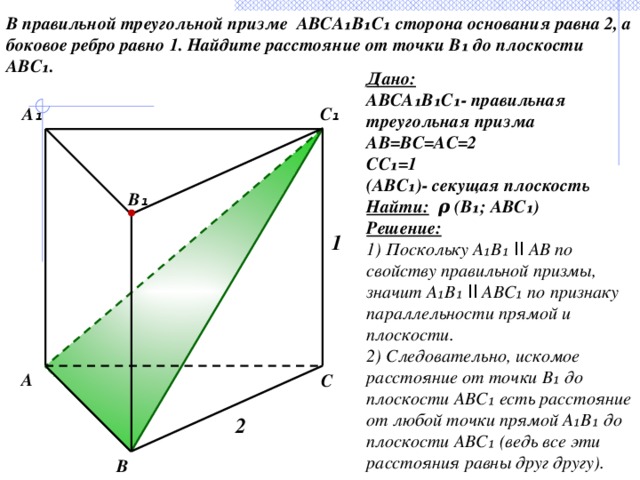
В правильной треугольной призме ABCA₁B₁C₁ сторона основания равна 2, а боковое ребро равно 1. Найдите расстояние от точки B₁ до плоскости ABC₁.

Дано:

ABCA₁B₁C₁- правильная треугольная призма

AB=BC=AC=2

CC₁=1

(ABC₁)- секущая плоскость

Найти: ρ (B₁; ABC₁)

Решение:

1) Поскольку А₁В₁ ІІ AB по свойству правильной призмы, значит А₁В₁ ІІ ABC₁ по признаку параллельности прямой и плоскости.

2) Следовательно, искомое расстояние от точки B₁ до плоскости ABC₁ есть расстояние от любой точки прямой A₁B₁ до плоскости ABC₁ (ведь все эти расстояния равны друг другу).

A ₁

C ₁

B ₁

1

A

C

2

B

4

3) Поэтому мы можем выбрать наиболее удобную точку на прямой А₁В₁.

Это точка N- середина А₁В₁.

Найдем расстояние от точки N до плоскости ABC₁.

4) Пусть М- середина АВ.

5) Соединим N с М и N с С₁.

6) ∆АС₁В- равнобедренный с основанием АВ, АС₁=ВС₁– по свойству правильной призмы

С₁М- медиана.

7) В ∆MNC₁ проведем NH ┴ MC₁. И докажем, что NH ┴ АВC₁.

8) АВ ┴ С₁М, т.к. медиана С₁М в равнобедренном треугольнике ∆АВС₁ является и высотой.

АВ ┴ MN т.к. призма прямая.

MN ∩ MC₁=M, MN  MNC₁,

MC ₁  MNC ₁ .

A ₁

C ₁

N

B ₁

1

H

C

A

2

M

B

Значит, AB ┴ MNC₁ на основании признака перпендикулярности прямой и плоскости.

4

9) Следовательно, АВ перпендикулярна любой прямой лежащей в плоскости MNC ₁ ,

A ₁

т.е. AB ┴ NH.

10) Итак,

NH ┴ C ₁ M (построению) и

NH ┴ AB ( по доказанному)

АВ ∩ МС ₁ =М, АВ  АВС ₁ ,

МС ₁  АВС ₁ .

По признаку перпендикулярности прямой и плоскости NH ┴ ABC ₁ .

11) Значит, длина NН- есть расстояние от точки N до плоскости АВС ₁.

12) Найдем NН:

C ₁

N

B ₁

1

H

A

C

2

M

B

С ₁

∆ С ₁ NM- прямоугольный, т.к. призма прямая.

A ₁

C ₁

H

N

B ₁

M

N

1

1

С другой стороны

H

Из этих двух равенств получаем:

A

C

2

M

B

∆ C ₁ NВ ₁ - прямоугольный

C ₁

C ₁

A ₁

2

N

B ₁

B ₁

1

N

1

По теореме Пифагора:

H

A

C

2

M

B

∆ C ₁ NM- прямоугольный

С ₁

2

A ₁

C ₁

H

N

B ₁

M

1

N

1

Так как

H

то

A

C

2

M

B

Ответ:

C ₁

Второй способ вычисления NH:

∆ С₁HN - прямоуголь ный

2

H

∆ С₁NM- прямоугольный

M

N

1

Третий способ вычисления NH:

∆ C₁HN ~ ∆C₁NM- по двум углам

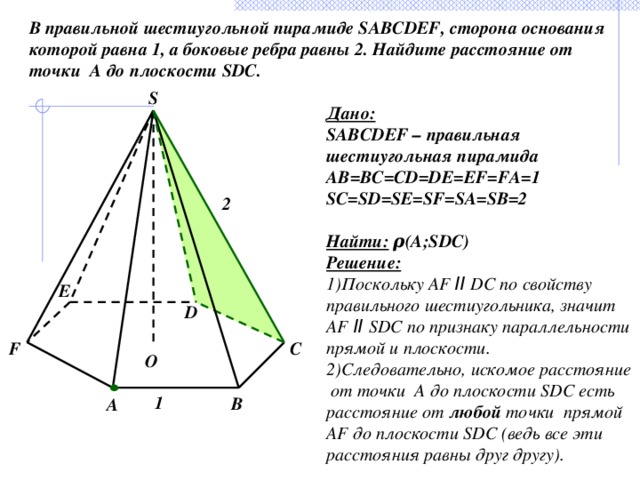
В правильной шестиугольной пирамиде SABCDEF, сторона основания которой равна 1, а боковые ребра равны 2. Найдите расстояние от точки A до плоскости SDC.

S

Дано:

SABCDEF – правильная

шестиугольная пирамида

AB=BC=CD=DE=EF=FA=1

SC=SD=SE=SF=SA=SB=2

Найти: ρ(A;SDC)

Решение:

1)Поскольку AF ІІ DC по свойству правильного шестиугольника, значит AF ІІ SDC по признаку параллельности прямой и плоскости.

2)Следовательно, искомое расстояние от точки A до плоскости SDC есть расстояние от любой точки прямой AF до плоскости SDC (ведь все эти расстояния равны друг другу).

2

E

D

C

F

O

1

B

A

11

3)Поэтому мы можем выбрать наиболее удобную точку на прямой AF.

Эта точка K – середина AF.

Найдем расстояние от точки K до плоскости SDC.

4)KO – радиус вписанной окружности в правильный шестиугольник, то KO ┴ AF.

А так как AF ІІ DC и KO ┴ AF , значит, прямая KO ┴ DC на основании свойства параллельных прямых.

5)Точку пересечения KO и DC обозначим M, M – середина DC.

6)Проведем апофемы SM и SK.

7)В ∆SKM проведем KH ┴ SM.

Докажем, что KH ┴ (SDC)

8)CD ┴ KM по доказанному

CD ┴ SM, т.к. ∆SDC – равнобедренный,

SM – медиана и высота.

KM ∩ SM=M, KM  (SKM), SM  (SKM)

Значит, CD ┴ KMS на основании признака перпендикулярности прямой и плоскости.

S

2

H

E

D

M

F

C

O

K

1

B

A

9)Значит CD перпендикулярна любой прямой лежащей в этой плоскости, т.е. CD ┴ KH.

10)А так как KH ┴ SM по построению и KH ┴ CD по доказанному, SM ∩ DC=M, SM  (SDC), DC  (SDC),

то KH ┴(SDC) на основании признака перпендикулярности прямой и плоскости.

11)Значит, длина KH – расстояние от точки K до плоскости SDC.

12)Найдем KH.

S

2

H

E

D

M

F

C

O

K

1

B

A

∆ SOB – прямоугольный.

OB – радиус описанной окружности.

S

S

2

По теореме Пифагора

2

B

O

1

H

E

D

M

F

C

O

K

1

B

A

S

С другой стороны:

S

2

∆ SMC – прямоугольный

C

M

2

По теореме Пифагора

H

E

D

M

F

C

O

K

1

B

A

Из равенств (1) и (2)

S

получаем:

2

H

E

D

M

F

C

O

K

1

B

A

Ответ:

Второй способ вычисления KH:

S

Запишем теорему косинусов для стороны KM в ∆SKM и найдем cos KSM, ∆SKM – равнобедренный:

H

M

K

Из основного тригонометрического тождества:

S

H

∆ KHS -прямоугольный

M

K

Задачи для самостоятельного решения

• В прямой треугольной призме ABCA ₁ B ₁ C ₁ известны ребра: AB = AC = 5, BC = 6, AA ₁ = 3. Найдите расстояние от точки C ₁ до плоскости A ₁ BC. Ответ:

• В правильной четырехугольной пирамиде SABCD (с вершиной S) сторона основания равна 6, а боковое ребро равно 5. Найдите расстояние от точки A до плоскости BCS.

Ответ:

• В правильной шестиугольной пирамиде SABCDEF (с вершиной S) сторона основания равна 2, а боковое ребро равно . Найдите расстояние от точки A до плоскости BCS.

Ответ :

• В правильной шестиугольной пирамиде SABCDEF (с вершиной S) сторона основания равна , а боковое ребро равно . Найдите расстояние от точки A до плоскости CDS.

Ответ: