Муниципальное казенное общеобразовательное учреждение
«Богучарская средняя общеобразовательная школа № 1»
Научно-исследовательская работа
по теме: « Уравнения высших степеней»
Автор: Жуковская Татьяна Владимировна , 9 «Б» класс
Руководитель: Алабина Галина Юрьевна
Богучар 2017
Содержание
Историческая справка……………………………………………………….….3
Введение…………………………………………………………………….…...4
Цели и задачи работы………………………………………...…………..……..5
Великие учёные, изучавшие уравнения высших степеней….…….................6
Виды уравнений высших степеней………………………………………...….9
Методы решения высших степеней……………….………………..…………9
Решение уравнений разными способами..………………….…………….....10
Вывод..………………………………………………………………………….30
Историческая справка
Решение уравнений высших степеней – история полная драматизма, разочарования и радости открытия. В течение почти 700 лет математики разных стран пытались найти приёмы решения уравнений третьей, четвёртой и более высоких степеней.
Только в 11 веке таджикский поэт и ученый Омар Хаям впервые решил уравнение III степени. Установить, существует ли формула для нахождения корней любого уравнения, пытались многие. В конце 18 века французский ученый Луи Лагранж пытался доказать невозможность алгоритма общих уравнений, а вначале 19 века француз Галуа развил идею Лагранжа.
С тех пор математика пошла другим путем. Ученые стали искать другие методы решения уравнений высших степеней.
Введение
Математическое образование, получаемое в общеобразовательной школе, является важнейшим компонентом общего образования и общей культуры современного человека. Практически все, что окружает современного человека – это все так или иначе связано с математикой. А последние достижения в физике, технике и информационных технологиях не оставляют никакого сомнения, что и в будущем положение вещей останется прежним. Поэтому решение многих практических задач сводится к решению различных видов уравнений, которые необходимо научиться решать.
Практика олимпиад, выпускных и вступительных экзаменов по математике показывает, что довольно часто приходится сталкиваться с уравнениями высших степеней. Решение таких уравнений зачастую вызывает большие трудности. Не все уравнения удается решить. В школьных учебниках уравнение высшей степени – редкость. Поэтому я выбрала эту тему для своей исследовательской работы.
Цели работы: Узнать какие методы решения высших степеней существуют; Научиться решать уравнения высших степеней различными способами.
Задачи:
1.Подобрать необходимую литературу
2.Отобрать материал для исследования, выбрать главную, интересную, понятную информацию
3.Проанализировать и систематизировать полученную информацию
4.Найти различные методы и приёмы решения уравнений высших степеней
5.Классифицировать исследуемые уравнения
6.Оформить работу в виде буклета
7.Создать электронную презентацию работы для представления собранного материала
Объект исследования: уравнения высших степеней
Методы исследования: изучение и анализ литературы, сравнение, обобщение, практический метод
Результат исследования: Я научилась решать возвратные и однородные уравнения,а также изучила теорему Безу и схему Горнера.
Гипотеза:Существует много различных видов и методов решения уравнений высших степеней, о которых не рассказывается в школьной программе 9 класса.
Великие учёные, изучавшие уравнения высших степеней

Омар Хайям (ок. 1048- ок. 1123)
Описал всевозможные виды уравнений третьей степени и рассмотрел сложные и красивые способы геометрических построений для отыскания их решения.

Никколо Тарталья (1499-1557)
Он вывел формулы для решения уравнений 3-ей степени, но своё открытие держал в тайне.

ДжероламоКардано(1501-1576)
Обращался к Тарталье с просьбой сообщить ему формулу для решения кубических уравнений и обещал хранить её в секрете. Он не сдержал слово и опубликовал формулу, указав, что Тарталье принадлежит честь открытия «такого прекрасного и удивительного, превосходящего все таланты человеческого духа».

Нильс Хенрик Абель (1802-1829)
В 1826 году доказал, что нельзя вывести формулы для решения уравнений пятой степени и выше.

Этьен Безу (1730-1783)
Французский математик, член Парижской академии наук. Преподавал математику в Училище гардемаринов в 1763 и Королевском артиллерийском корпусе в 1768. Основные его работы относятся к алгебре (исследование систем алгебраических уравнений высших степеней, исключение неизвестных в таких системах и др.) Является автором шеститомного «Курса математики» (1764-1769).

Уильям Джордж Горнер (1786 – 1837)
Английский математик. Основные труды по теории алгебраических уравнений. С его именем связана (1819) схема Горнера деления многочлена на двучлен .
Виды уравнений высших степеней
Уравнения третьей степени
Уравнения четвёртой степени
Уравнения пятой степени
Биквадратные уравнения
Возвратные уравнения
Однородные уравнения
Способы решения уравнений высших степеней
Разложение многочлена на множители:
Способ группировки
По формулам сокращенного умножения
По теореме Безу
Схема Горнера
Метод введения новой переменной
Биквадратные уравнения
Возвратные уравнения
Функционально-графический метод
Способ группировки.
Данный способ применяют к многочленам, которые не имеют общего множителя для всех членов многочлена. Чтобы разложить многочлен на множители способом группировки, нужно: Объединить члены многочлена в такие группы, которые имеют общий множитель в виде многочлена. Вынести этот общий множитель за скобки.
Примеры решения уравнений способом группировки:
x³-5x²-16x+80=0
x(x²-16)-5(x²-16)=0
(x-5)(x²-16)=0
(x-5)(x-4)(x+4)=0
x-5=0 или x-4=0 или x+4=0
x=5 x=4 x=-4
Ответ: -4; 4; 5.
x³-3x²-4x+12=0
x²(x-3)-4(x-3)=0
(x²-4)(x-3)=0
(x-2)(x+2)(x-3)=0
x-2=0 или x+2=0 или x-3=0
x=2 x=-2 x=3
Ответ: -2; 2; 3.
x⁴-5x³-16x²+100x-80=0
x⁴-5x³-20x²+4x²+100-80=0
x²(x²-20)-5x(x²-20)+4(x²-20)=0
(x²-5x+4)(x²-20)=0
x²-5x+4=0 или x²-20=0
D=25-16=9 x²=20
x1=(5+3)÷2=4x=±√20
x2=(5-3)÷2=-1
Ответ:-√20; -1; 1; √20.
По формулам сокращенного умножения
1. Квадрат суммы: (a + b)2 = a2 + 2ab + b2
2. Квадрат разности: (a - b)2 = a2 - 2ab + b2
3. Разность квадратов: а2- b2 = (a - b) (a + b)
4. Куб суммы: (a + b)3 = a3 + 3a2b + 3ab2 + b3
5. Куб разности: (a - b)3 = a3 - 3a2b + 3ab2 - b3
6. Сумма кубов: a3 + b3 = (a + b) (a2 - ab + b2)
7. Разность кубов: a3 - b3 = (a - b) (a2 + ab + b2)
Примеры решения уравнений с помощью формул сокращённого умножения:
(2x)³-8=0
(2x)³-2³=0
(2x-2)(4x²+4x+4)=0
2x-2=0 или 4x²+4x+4=0
x=1 D=16-64=-48-корней нет
Ответ: 1.
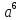 +18a⁴+108a²+216=0
+18a⁴+108a²+216=0
(a²+6)³=0
a²+6=0
a²=-6
Ответ: корней нет.
8x(1+2x)-(4x+3)(4x-3)=2x.
8x+16x2-(16x2-9)=2x,
8x+16x2-(16x2-9)=2x,
8x+16x2-16x2+9=2x,
8x-2x=-9,
6x=-9,
x=-1,5
Ответ: -1,5
Метод введения новой переменной
Одинаковые составляющие части уравнения, содержащие переменные заменить на новую переменную.
Примеры решения уравнения методом введения новой переменной:
(x2+4x)(x2+4x-17)=-60
Пусть  = t, тогда
= t, тогда
t( t – 17 ) = -60
 - 17t = -60
- 17t = -60
t2 - 17t + 60 = 0
 = 5
= 5
 = 12
= 12
При t = 5, 
 = 1
= 1
 = -5
= -5
При t = 12, 
 = 2
= 2
 = -6
= -6
Ответ: -6, -5, 1, 2.
(x-3)(x-4)(x-5)=(x-2)(x-4)(x-5)
Пусть (x-4)(x-5)=t, тогда
t(x-3)= t(x-2)
tx-3t = tx-2t
tx-3t-tx+2t = 0
-t = 0
t = 0
Вернёмся к замене:
(x-4)(x-5)= 0
x-4 = 0 x-5 = 0
x=4 x=5
Ответ: 4; 5.
(x2-5x+7)(x-2)(x-3)=0
(x2-5x+7)(x2-5x+6)=0
Пусть х2-5=t, тогда
(t+7)(t+6)=0
t1= -7
t2= -6
Вернёмся к замене:
х2-5=-7 х2-5=-6
x2= -12 x2=-11
Ответ: корней нет.
Биквадратные уравнения.
К квадратным уравнениям сводятся уравнения четвертой степени: ax4 + bx2 + c = 0, называемые биквадратными, причем, а ≠ 0. Достаточно положить в этом уравнении х2 = y, следовательно, ay² + by + c = 0. Найдём корни полученного квадратного уравнения y1,2 = 
заменим y на x и получим 
Примеры решения биквадратных уравнений:
2x⁴-19x²+9=0
Пусть y=x², тогда
2y²-19y+9=0
y1=9
y2=0,5
Вернёмся к замене:
При у=9, x²=9
x=±√9
x=±3
При у=0,5, х²=0,5
х=±√0,5
Ответ:-3; -√0,5; √0,5; 3.
10х4-12х2+1=-10х4
10х4+10х4-12х2+1=0
20х4-12х2+1=0
Пусть х2=t, тогда
20t2-12t+1=0
D=144-80=64
t1=0,5
t2=0,1
Вернёмся к замене:
При t=0,5, x²=0,5
x=±√0,5
При t=0,1, х²=0,1
х=±√0,1
Ответ: -√0,1; -√0,5; √0,1; √0,5.
(х-4)4-5(х-4)2= -4
(х-4)4 -5(х-4)2 +4=0
Пусть (х-4)2=t
t2-5t+4=0
D=25-16=9
t1=4
t2=1
Вернёмся к замене:
При t=4, (х-4)2 =4
x1=6
x2=2
При t=1, (х-4)2=1
x1=5
x2=3
Ответ:2; 3; 5; 6.
Функционально-графический метод
Метод основан на использовании графических иллюстраций или каких-либо свойств функций. В одной системе координат строим графики функций, записанные в левой и в правой частях уравнения, затем, находим точку (точки) их пересечения. Абсцисса найденной точки является решением уравнения.
Примеры решения уравнений функционально-графическим методом:
Решить уравнение√х=
Построим в одной системе координат графики функций y= и y=
и y=
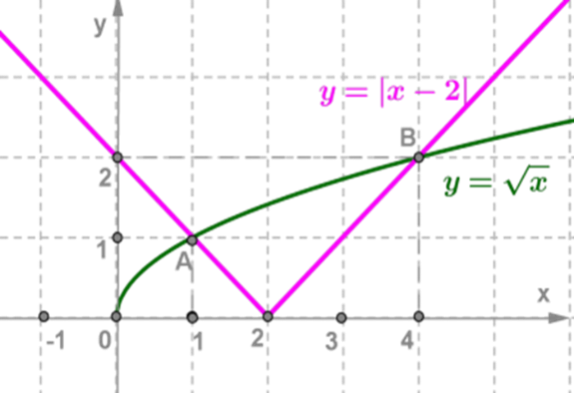
Они пересекаются в двух точках A(1;1) и B(4;2).
Значит, уравнение имеет два корня: х1=1, х2=4.
Ответ: 1;4.
Решение уравнение х3-√х=0.
Построим в одной системе координат графики функций y= х3 и y=√х
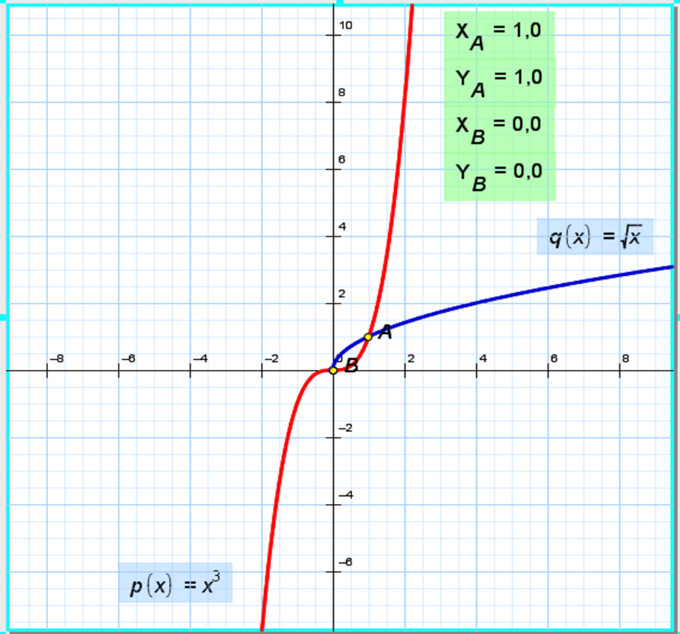
Они пересекаются в двух точках A(1;1) и B(0;0).
Значит, уравнение имеет два корня: х1=1, х2=0.
Ответ: 1;0.
Решить уравнение  = -х2 -1
= -х2 -1
Построим в одной системе координат графики функций y=-х2 -1 и y=
Они не пересекаются .
Значит, уравнение не имеет корней.
Ответ: корней нет.
Корень многочлена
Если все коэффициентыa0, a1, … , an( an 0) многочлена
0) многочлена
Pn(x)=anxn+ an-1xn-1+…+ a1x+a0
Целые числа и рациональное число (
( -несократимая дробь,
-несократимая дробь, ;
; ) является корнем многочлена, то коэффициент a0 делится на p, а коэффициент an делится на q.
) является корнем многочлена, то коэффициент a0 делится на p, а коэффициент an делится на q.
По теореме Безу
Остаток от деления многочлена Р(х) на двучлен (х – а) равен Р(а).
Следствие из теоремы Безу: Число a является корнем многочлена P(x) тогда и только тогда, когда P(x) делится на (x ‑ a) безостатка.
Примеры решения уравнений с помощью теоремы Безу:
Решить уравнение 2х3-3х2+5х-14=0
Возможные рациональные корни: ± ; ±1; ±2; ±
; ±1; ±2; ± ; ±7; ±14.
; ±7; ±14.
P(x)=2х3-3х2+5х-14 = 0
P(1)= 2 – 3 + 5 – 14 0
0
P(-1)= -2 – 3 – 5 - 14 0
0
P(2)=16 – 12 + 10 - 14 = 0
(x-2)( 2х2+х+7)=0
x = 2D=1-56=-55
корней нет
Ответ: 2.
Решить уравнение 3х4 – 2х3 -8х2 – х + 2 = 0
Возможные рациональные корни: ± ; ±
; ± ; ±1 ; ±2.
; ±1 ; ±2.
P(x)= 3х4 – 2х3 -8х2 – х + 2 = 0
P(1)= 3 – 2 – 8 – 1+ 2  0
0
P(-1)=3 + 2 – 8 + 1 +2 = 0
(х+1)(3х3-5х2-3х+2)=0
Решим уравнение 3х3 – 5х2 – 3х + 2 = 0.
Возможные рациональные корни: ± ; ±1; ±
; ±1; ± ; ± 2 .
; ± 2 .
P(x)=3х3 – 5х2 – 3х + 2 = 0
P(1)= 3 – 5 – 3 + 2 0
0
P(-1)= - 3 – 5 + 3 – 2  0
0
P(2)= 24 – 20 – 6 + 2 = 0
(х+1)(х-2)(3х2+х-1)=0
х+1=0 х-2=0 3х2+х-1=0
х= -1 х= 2 D=1+12=13
х1=
х2=
Ответ: -1; ;
;  ; 2.
; 2.
Решить уравнение x3 - 2x2 - 6x + 4=0
Возможные рациональные корни: ±1 ; ± 2 ; ±4.
P(x)= x3 - 2x2 - 6x + 4 = 0
P(1)= 2 – 2 – 6 + 4 0
0
P(-1)= - 1 – 2 + 6+ 4 0
0
P(2)= 8 – 8 – 12 + 4 0
0
P(- 2)= - 8 – 8+ 12 + 4 = 0
(х+2)( х2-4х+2) = 0
х+2=0 х2-4х+2 = 0
х= -2 D=16-8= 8
х1=
х2=
Ответ: -2;  ;
;  .
.
Схема Горнера
Схема Горнера - это алгоритм вычисления значения многочлена при определенном значении переменной. Использование схемы Горнера значительно упрощает вычисления, а также помогает эффективно подбирать корни.
Примеры решения уравнений с помощью схемы Горнера:
Решить уравнение: 4х3 - 19х2 + 19х + 6=0
Возможные рациональные корни уравнения:± ; ±
; ± ; ±
; ± ; ±1; ±
; ±1; ± ; ±2; ±3; ±6.
; ±2; ±3; ±6.
P(x)=4х3 - 19х2 + 19х + 6 = 0
P(1)= 4 – 19 + 19 + 6 ≠ 0
0
P(-1)= -4 – 19 – 19 + 6 ≠ 0
0
P(2)=32–76+38+6=0
Остаток равен 0, значит:
(х-2)(4х2-11х-3)=0
x = 2 D= 121 + 48 = 169
х1=3
х2= -0,25
Ответ:-0,25, 2, 3.
Решить уравнение: 5х3 +5х2 +х – 11 = 0
Возможные рациональные корни уравнения:  .
.
P(x)=5х3 +5х2 +х – 11= 0
P(1)= 5+5 + 1 – 11 = 0
(х-1)(5х2+10х+11)=0
х-1=0 5х2+10х+11=0
х=1 D=100 - 220=-120
корней нет
Ответ: 1.
Решить уравнение: х3 - 7х - 6=0
Возможные рациональные корни уравнения: ±1; ±2; ±3; ±6.
P(x)= х3 - 7х – 6 = 0
P(1)= 1 – 7 – 6 ≠ 0
P(-1)= - 1 + 7 – 6 = 0
(х+1)(х2-х+6) = 0
х+1=0 х2-х+6 = 0
х= -1 D= 1- 4= -3
корней нет
Ответ: -1.
Возвратные уравнения
Возвратное уравнение – алгебраическое уравнение
а0хn + a1xn – 1 + … + a1x +a0=0, в котором ак = an – k,
где k = 0, 1, 2 …n, причем, а ≠ 0.
Задачу нахождения корней возвратного уравнения сводят к задаче нахождения решений алгебраического уравнения меньшей степени. Термин возвратные уравнения был введён Л. Эйлером.
Алгоритм решения:
Разделить левую и правую части уравнения на х2.
Группировкой привести полученное уравнение к виду ;
;
Ввести новую переменную t = , тогда выполненоt2 = x2+2+
, тогда выполненоt2 = x2+2+ , то есть x2+
, то есть x2+ = t2-2
= t2-2
В новых переменных рассматриваемое уравнение является квадратным: at2 +bt+c = 0
Решить его относительно t, возвратиться к исходной переменной.
Примеры решения возвратных уравнений:
2х⁴+9х³-х²+9х+2=0
Т.к. х = 0 не является корнем уравнения, то уравнение можно разделить на х², получив 2х²+9х-1+ +
+ = 0
= 0
2(х²+ )+9(х+
)+9(х+ )-1=0
)-1=0
Сделаем замену у=х+ ; у²-2=х²+
; у²-2=х²+
Тогда 2(у²-2)+9у-1=0
у1=-5
у2=0,5
Вернёмся к замене:
При у=-5, x²=-5
корней нет
При у=0,5, х²=0,5
х=±√0,5
Ответ:-√0,5; √0,5.
6х4-35х3+62х2-35х+6=0
Т.к. х = 0 не является корнем уравнения, то уравнение можно разделить на х², получив 

Сделаем замену у=х+ ; у²-2=х²+
; у²-2=х²+
6у2-35у+50=0
D=1225-1200=25
у1=
у2=
Вернёмся к замене:
При у= , х+
, х+ =
=
х1=3
х2=
При у= , х+
, х+ =
=
х1=2
х2=
Ответ:  ;
;  ; 2; 3.
; 2; 3.
3х4-2х3+4х2-4х+12=0
Т.к. х = 0 не является корнем уравнения, то уравнение можно разделить на х², получив 3х2-2х+4- =0
=0

Сделаем замену у=х+ ; у²-4=х²+
; у²-4=х²+
3(у2-4)-2у+4=0
3у2-2у-8=0
D=4+96=100
у1=2
у2= -
Вернёмся к замене:
При у=1
х+ =4
=4
Корней нет.
При у= -
х+ = -
= -
Корней нет.
Ответ: корней нет.
Однородные уравнения
Однородные уравнения – это такие уравнения, у которых в левой части находятся одночлены одной степени, а правая часть равна нулю.
-это уравнение однородное третьей степени. Чтобы решить однородное уравнение, нужно обе его части разделить на одно из неизвестных в степени каждого многочлена, с учетом, что он не равен нулю.
Примеры решения однородных уравнений:
х2-7ху+10у2=0
Найдите .
.
Разделим уравнение на у2.


Пусть = t, тогда
= t, тогда
t2 - 7t + 10=0
D = 49 – 40 = 9
t1= 5
t2= 2
Вернёмся к замене:
 = 2 или
= 2 или  = 5
= 5
Ответ: 2; 5.
3х2-2ху-у2=0
Найдите .
.
Разделим уравнение на у2.


Пусть = t, тогда
= t, тогда
3t2-2t-1=0
D=16
t1=3
t2= -
Вернёмся к замене:
 = 3 или
= 3 или  =
= 
Ответ:  ; 3.
; 3.
3х2+
Найдите ху.
3х2у2+5ху-8=0
Пусть ху= t
3t2+5t-8=0
D=25+96=121
t1=1
t2=
Вернёмся к замене:
ху= 1
ху= 
Ответ:  ; 1.
; 1.
Вывод:
Моя гипотеза, выдвинутая в начале работы, оказалась верна. В ходе исследовательской работы я научилась решать однородные и возвратные уравнения, познакомилась с теоремой Безу и схемой Горнера, а также узнала о многих учёных, которые внесли большой вклад в историю математики. По-моему мнению, интерес учащихся в первую очередь вызывает возможность подбора уравнений при помощи достаточно простого алгоритма с использованием схемы Горнера. Также учащиеся интересуются различными стандартными типами замены переменных, которые позволяют существенно упрощать вид задачи, но особый интерес обычно вызывают графические методы решения.













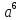 +18a⁴+108a²+216=0
+18a⁴+108a²+216=0 = t, тогда
= t, тогда - 17t = -60
- 17t = -60 = 5
= 5 = 12
= 12
 = 1
= 1 = -5
= -5

 и y=
и y=


 = -х2 -1
= -х2 -1









