Научно-исследовательская работа "Треугольник Рёло"

Муниципальное казенное общеобразовательное учреждение

«Богучарская средняя общеобразовательная школа № 1»

Научно-исследовательская работа

по теме: «Треугольник Рёло»

Автор: Пономарёва Валерия Витальевна, 9 «А» класс

Руководитель: Алабина Галина Юрьевна,

Нащёкина Ольга Владимировна

Богучар 2016 г.

СОДЕРЖАНИЕ

1. Введение………..………………………………………………………………....2

2. Понятие треугольника Рёло ……….……...…………………………….…….....4

3. Свойства треугольника Рёло……………………………….................................6

4. История появления………………………….…………………………………....9

5. Практическое применение………………………………………………….…..10

5.1. Сверление квадратных отверстий…………………...………………....10

5.2. Двигатель Ванкеля……………………………….…………………..…10

5.3. Крышки для люков…………..………..………………………………...11

5.4. Грейферный механизм в кинопроектах…………………………….….12

5.5.Плектр…………………………………………..……………….………..12

6. Треугольник Рёло в искусстве…………………………………..………...…….13

6.1. Треугольник Рёло в архитектуре……………...……………………….13

6.2. Изобретение велосипеда с треугольными колёсами…..……………...13

6.3. Повозка с треугольными колёсами…………………………………….15

7. Заключение………………………….……………………………………...…….17

8.Список литературы…………………………..………………………………...…18

1. Введение

Иногда в основе любой ширины и толщины нужно сделать отверстие с идеальным квадратным сечением. А вы когда-нибудь задумывались над тем, как сверлят квадратные отверстия? Советов, как добиться максимальной точности при минимальных затратах, множество. Я задумалась над вопросом, а как бы с этой задачей справился математик и смог бы он сделать лучше. Ответ оказался положительным. Оказывается, существует еще один способ для вырезания квадратных отверстий, в реализации которого косвенно поучаствовал математик. Итак, квадратные отверстия можно сделать при помощи специального сверла, в сечение которого заложена форма треугольника Рёло. Меня заинтересовало не только само по себе данное изобретение, но и необычная геометрическая фигура – круглый треугольник. Я узнала, что он называется треугольником Рёло и посвятила свою работу изучению его свойств и областей применения. А заодно поставила задачу выяснить, как геометрия позволяет этому чуду катиться и иметь удивительно плавный ход.

Область исследования – математика.

Объект исследования– треугольник Рёло.

Предмет исследования – понятие треугольника Рёло, его свойства и практическое применение.

Цель исследования:

Привести  достаточное  количество  примеров  применения  свойств  треугольника  Рёло.

Задачи:

1. Изучить главные свойства и узнать как можно больше о треугольнике Рёло.

2. На основе изученных материалов предложить области использования треугольника Рёло.

3. Познакомиться с историей изобретения.

4. Рассмотреть области применения фигур постоянной ширины.

Актуальность:

В современном мире, при быстро развивающихся технологиях нельзя обойти  стороной фигуру постоянной ширины - треугольник Рёло, позволяющий сократить затраты при производстве, к примеру, при конструировании деталей.

2. Понятие треугольника Рёло.

Треугольник Рёло представляет собой область пересечения трёх равных кругов с центрами в вершинах правильного треугольника и радиусами, равными его стороне.

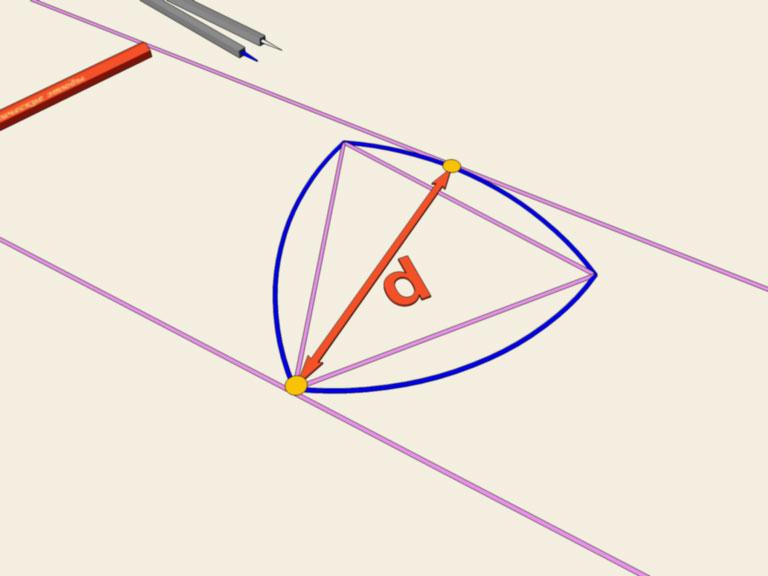
Построение треугольника Рёло циркулем

Треугольник Рёло можно построить с помощью одного только циркуля, не прибегая к линейке. Это построение сводится к последовательному проведению трёх равных окружностей. Центр первой выбирается произвольно, центром второй может быть любая точка первой окружности, а центром третьей — любая из двух точек пересечения первых двух окружностей.

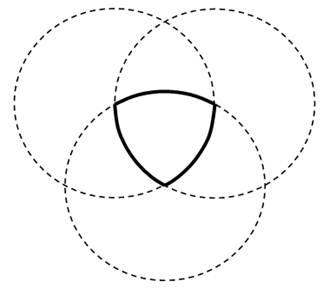
3. Свойства треугольника Рёло.

Он обладает свойством кривых постоянной ширины.

Треугольник Рело - плоская фигура постоянной ширины — его можно вращать между двух параллельных прямых, расположенных на фиксированном расстоянии друг от друга, и он будет постоянно касаться их обеих. Добавим еще пару параллельных прямых, касающихся треугольника Рело и образующих с уже имеющимися прямой угол. Тем самым получим квадрат. Если вращать треугольник Рело специальным образом, то он будет постоянно находиться внутри квадрата и в любой момент касаться всех его сторон. Если быть более точным, то надо рассматривать квадрат с немного скругленными углами. При этом треугольник Рело является в этом «квадрате» ротором минимальной площади – той фигурой, которая при любом повороте будет касаться всех сторон, и при этом более маленькой по площади фигуры с таким условием не существует. Кроме окружности и треугольника Рело бывают и другие фигуры постоянной ширины. На любом правильном нечетном n–угольнике, так же как и на треугольнике, можно построить кривую постоянной ширины. Бывают несимметричные кривые постоянной ширины. Но бывает и бесконечно много фигур постоянной ширины, построенных именно на правильном треугольнике, и не подобных ни друг другу, ни треугольнику Рело.

Теорема Барбье: Все кривые постоянной ширины h имеют одинаковую длину, равную πh.

Треугольника Рёло симметричен, обладает осевой симметрией. Он имеет три оси симметрии, каждая из которых проходит через вершину треугольника и середину противоположной стороны.

Поскольку треугольник Рёло является фигурой постоянной ширины, он обладает всеми общими свойствами фигур этого класса:

– с каждой из своих опорных (параллельных) прямых треугольник Рёло имеет лишь по одной общей точке;

– расстояние между двумя любыми точками треугольника Рёло не может превышать его ширины;

– отрезок, соединяющий точки касания двух параллельных опорных прямых к треугольнику Рёло, перпендикулярен к этим опорным прямым;

– через любую точку границы треугольника Рёло проходит по крайней мере одна опорная прямая;

– через каждую точку границы треугольника Рёло проходит объемлющая его окружность радиуса , причём опорная прямая, проведённая к треугольнику Рёло через точку , является касательной к этой окружности;

– треугольник Рёло, как и любую другую фигуру постоянной ширины, можно вписать в квадрат.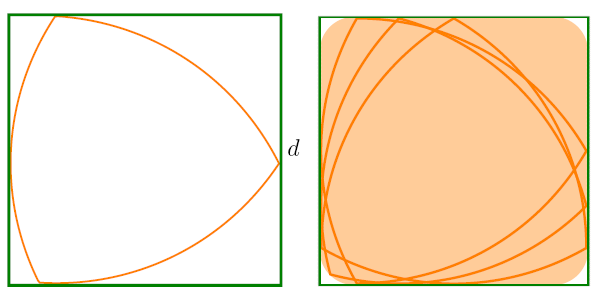

Экстремальные свойства

–Среди всех фигур постоянной ширины у треугольника Рёло наименьшая площадь. Чтобы найти площадь треугольника Рёло, можно сложить площадь внутреннего равностороннего треугольника и площадь трёх оставшихся одинаковых круговых сегментов, опирающихся на угол в 60°.

– Наименьший угол. Через каждую вершину треугольника Рёло, в отличие от остальных его граничных точек, проходит не одна опорная прямая, а бесконечное множество опорных прямых. Пересекаясь в вершине, они образуют «пучок». Угол между крайними прямыми этого «пучка» называется углом при вершине. Для фигур постоянной ширины угол при вершинах не может быть меньше 120°. Единственная фигура постоянной ширины, имеющая углы, равные в точности 120° — это треугольник Рёло.

4. История появления:

По мнению историков, название это «непростой» простой фигуре дал немецкий механик Франц Рёло. Франц Рело родился 30 сентября 1829 г. в Эшвейлере, близ Ахена, в семье, для которой техника была традиционным занятием.Многие историки сходятся в том, что именно он стал первооткрывателем свойств этой геометрической фигуры. Потому как он первый широко использовал свойства и возможности треугольника Рёло в своих механизмах. Следовательно, изобретенный в прошлом веке треугольник Рёло широко используется сегодня. Однако его изучение не стоит на месте. Его свойства, как характеристики простой фигуры, находится в постоянном теоретическом и практическом изучении.

5. Практическое применение.

1. Сверление квадратных отверстий

Сверло с сечением в виде треугольника Рело и режущими кромками, совпадающими с его вершинами, позволяет получать почти квадратные отверстия. Отличие таких отверстий от квадрата состоит лишь в немного скруглённых углах. Другая особенность подобного сверла заключается в том, что его центр при вращении не остаётся на месте, как это происходит в случае традиционных спиральных свёрл, а описывает кривую, состоящую из четырёх дуг эллипсов. Поэтому патрон, в котором зажато сверло, не должен препятствовать этому движению.

Впервые сделать подобную конструкцию удалось Гарри Уаттсу, английскому инженеру, работавшему в США. Для сверления он использовалнаправляющий шаблон с квадратной прорезью, в котором двигалось сверло, вставленное в «плавающий патрон». Патенты на патрон и сверло были получены Уаттсом в 1917 году. Продажу новых дрелей осуществляла фирма WattsBrothersToolWorks. Ещё один патент США на похожее изобретение был выдан в 1978 году.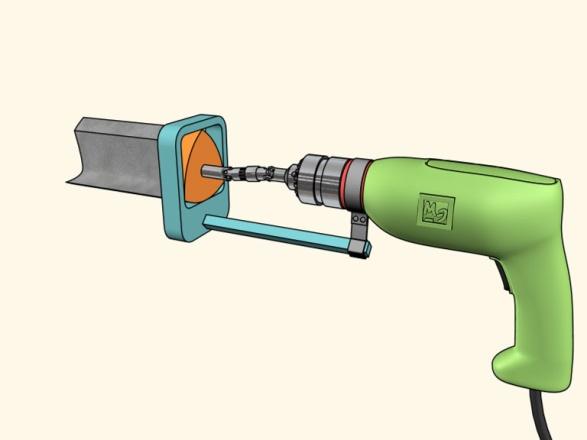

2. Двигатель Ванкеля

Другой пример использования можно найти в двигателе Ванкеля: ротор этого двигателя выполнен в виде треугольника Рёло. Он вращается внутри камеры, поверхность которой выполнена по эпитрохоиде. Вал ротора жёстко соединён с зубчатым колесом, которое сцеплено с неподвижной шестернёй. Такой трёхгранный ротор обкатывается вокруг шестерни, всё время касаясь вершинами внутренних стенок двигателя и образуя три области переменного объёма, каждая из которых по очереди является камерой сгорания. Благодаря этому двигатель выполняет три полных рабочих цикла за один оборот.

Двигатель Ванкеля позволяет осуществить любой четырёхтактный термодинамический цикл без применения механизма газораспределения. Смесеобразование, зажигание, смазка, охлаждение и пуск в нём принципиально такие же, как у обычных поршневых двигателей внутреннего сгорания.

Впервые на серийных автомобилях этот двигатель стала устанавливать компания Mazda. Он установлен на моделях MazdaRX-7 и MazdaRX-8.

3. Крышки для люков

В форме треугольника Рёло можно изготавливать крышки для люков — благодаря постоянной ширине они не могут провалиться в люк. В Сан-Франциско подобные крышки используются для системы рекуперированной воды.

4. Грейферный механизм в кинопроекторах

Также треугольник использовался в грейферном механизме в кинопроекторах. Двигатели дают равномерное вращение оси, а чтобы на экране было четкое изображение, пленку мимо объектива надо протянуть на один кадр, дать ей постоять, потом опять резко протянуть и так 18 раз в секунду. Именно эту задачу решает грейферный механизм. Он основан на треугольнике Рело, вписанном в квадрат и двойном параллелограмме, который не дает квадрату наклоняться в стороны.

Действительно, т.к. длины противоположных сторон равны, то среднее звено при всех движениях остается параллельным основанию, а сторона квадрата всегда параллельной среднему звену. Чем ближе ось крепления к вершине треугольника Рело, тем более близкую к квадрату фигуру описывает зубчик грейфера.

5. Плектр

Треугольник Рёло — распространённая форма плектра (медиатора): тонкой пластинки, предназначенной для приведения в состояние колебания струн щипковых музыкальных инструментов.

6. Треугольник Рёло в искусстве

1. Треугольник Рёло в архитектуре

Форма треугольника Рёло используется и в архитектурных целях. Окна в форме треугольника Рёло можно обнаружить в церкви Богоматери в Брюгге, а также в шотландской церкви в Аделаиде.

2. Изобретение велосипеда с треугольными колесами

1) Колесо, изобретенное несколько тысяч лет назад, произвело переворот в жизни человека. Постоянство ширины явилось для колеса определяющим свойством, следствием которого явилось техническое завоевание мира.«Изобретением велосипеда» называют бессмысленное повторение и переоткрытие давно пройденного и известного, и совершенно напрасно. Современные инженеры, можно сказать, постоянно изобретают велосипед, внося все новые усовершенствования в его конструкцию и отдельные детали. Однажды в интернете мы прочитали об одном удивительном изобретении китайского пенсионера – велосипеде с треугольными колесами.

Изобретением колес велосипеда занимается китайский рационализатор Гуань Байхуа, 50-летний офицер из города Циндао. Больше того, он изобретает заново самую консервативную деталь велосипеда – колеса. Вместо понятных всем круглых он предложил кататься на колесах пяти - и треугольной формы (спереди и сзади, соответственно). Для китайцев велосипед – главный вид транспорта, популярностью затмевающий автомобили. Но велосипед с угловатыми колесами средством передвижения не станет. По словам изобретателя, поездка на нем требует больше усилий, чем на обычном велосипеде, и скорее всего, он найдет свою нишу в качестве экзотической игрушки и более эффективного тренажера. Впрочем, все, кто пробовал прокатиться на нем, удивляются вовсе не трудности кручения педалей, а неожиданной плавности хода. 
Действительно, казалось бы, угловатые колеса неизбежно должны создавать при качении существенную тряску – но ее Гуаню Байхуа удалось снизить благодаря прекрасному знанию геометрии и настоящей китайской хитрости.

2) Изготовление велосипеда с помощью 3D ручки

3. Повозка с «треугольными» колесами.

Для перемещения тяжёлых предметов на небольшие расстояния можно использовать не только колёсные, но и более простые конструкции, например, цилиндрические катки. Для этого груз нужно расположить на плоской подставке, установленной на катках, а затем толкать его. По мере освобождения задних катков их необходимо переносить и класть спереди. Такой способ транспортировки человечество использовало до изобретения колеса. При этом перемещении важно, чтобы груз не двигался вверх и вниз, так как тряска потребует дополнительных усилий от толкающего. Для того, чтобы движение по каткам было прямолинейным, их сечение должно представлять собой фигуру постоянной ширины. Чаще всего сечением был круг, ведь катками служили обыкновенные брёвна. Однако сечение в виде треугольника Рёло будет ничуть не хуже и позволит передвигать предметы столь же прямолинейно.

Таким же образом можно устроить подвеску некруглого колеса и взяв четыре таких подвески, можно соорудить повозку. При этом она будет ехать совершенно без покачиваний! Чтобы убедиться, что тряски нет, можно поставить, как учат автомобилистские традиции, на тележку стакан с водой.

Я попробовала соорудить такую повозку и опытным путем проверить гипотезу об отсутствии качки.

7. Заключение

Несколько тысяч лет назад было изобретено колесо, которое произвело переворот в жизни человека. Определяющим свойством, следствием которого стало техническое завоевание мира, стало свойство постоянства ширины. Но, как оказалось, круг – не единственная фигура, которая обладает этим свойством. Вызвавший мой интерес, треугольник Рёло, также принадлежит этому семейству. В своей работе я не только изучила его свойства, геометрические характеристики, историю изобретения, но и рассмотрела сферы применения этой выпуклой, симметричной фигуры постоянной ширины.

Кроме этого, я сконструировала повозку с колесами в форме треугольника Рёло и проверила теорию об отсутствии качки.

На 3D принтере изобрела модель велосипеда с треугольными колесами и зафиксировала на видео результат моей работы.

Выдвинутая мной гипотеза о свойствах этой фигуры нашла свое подтверждение. Кроме того, я ответила на ряд вопросов познавательного характера. Не менее познавательной оказалась информация о сферах применения «круглого» треугольника не только в технике, но и в архитектуре.

Таким образом, изобретенный в прошлом веке треугольник Рёло широко используется сегодня. Однако его изучение не стоит на месте. Его свойства как характеристики фигуры постоянной ширины находятся в постоянном теоретическом и практическом изучении. И это правильно, ведь чем лучше будут изучены свойства треугольника Рёло и остальных фигур постоянной ширины, тем больше возможностей будет открываться для их использования в нашей жизни. Однако данный проект является лишь каплей в море в изучении данной темы, ведь столько интересного осталось за его рамками.Таким образом, поставленные мною задачи, реализованы в полном объеме.

Список использованной литературы

1. Дорофеев, Г.В., Шарыгин, И.Ф., Суворова, С.Б. Математика. – М.:Просвещение,1987.

2. Коксетер, С.М., Грейтцер, С.Л. Новые встречи с геометрией. – М., Наука, 1978.

3. В. Г. Болтянский, И. М. Яглом. Выпуклые фигуры. М.—Л.: ГТТИ, 1951.

4. Г. Радемахер, О. Теплиц. Числа и фигуры. М.: Физматгиз, 1962.

5. http://yandex.ru/images

6. http://www.etudes.ru/ru/etudes/koleso/