Навигация. Основные понятия и определения

параллель

нормаль

меридиан

параллель

(отвесная линия)

Земной экватор

Гринвичский

Земная ось

меридиан

меридиан

наблюдателя

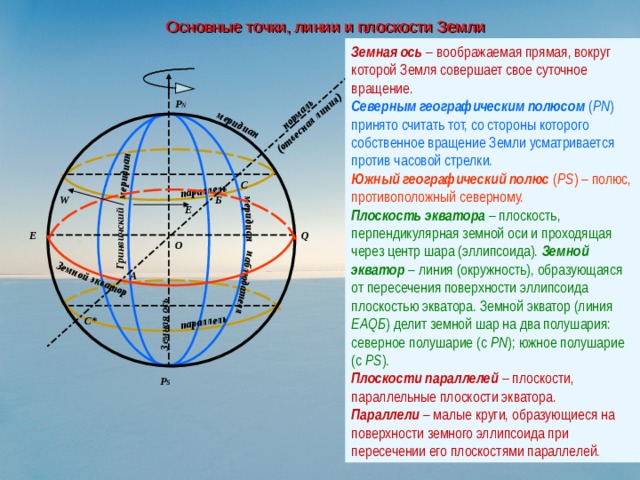
Основные точки, линии и плоскости Земли

Земная ось – воображаемая прямая, вокруг которой Земля совершает свое суточное вращение.

Северным географическим полюсом ( PN ) принято считать тот, со стороны которого собственное вращение Земли усматривается против часовой стрелки.

Южный географический полюс ( PS ) – полюс, противоположный северному.

Плоскость экватора – плоскость, перпендикулярная земной оси и проходящая через центр шара (эллипсоида). Земной экватор – линия (окружность), образующаяся от пересечения поверхности эллипсоида плоскостью экватора. Земной экватор (линия ЕАQБ ) делит земной шар на два полушария: северное полушарие (с PN ); южное полушарие (с PS ).

Плоскости параллелей – плоскости, параллельные плоскости экватора.

Параллели – малые круги, образующиеся на поверхности земного эллипсоида при пересечении его плоскостями параллелей.

P N

C

Б

W

E

E

Q

О

А

С *

P S

параллель

нормаль

меридиан

параллель

(отвесная линия)

Земной экватор

Гринвичский

Земная ось

меридиан

меридиан

наблюдателя

Основные точки, линии и плоскости Земли

Нормаль (отвесная линия) – прямая, совпадаю-щая с направлением силы тяжести в данной точке: для т. PN (или PS ) нормалью является земная ось « PNPS »; для т. Е (или Q ) нормалью является диаметр земного экватора; для т. С – нормалью является прямая линия СОС  , проходящая через центр Земли. Плоскости истинных меридианов – плоскости, проходящие через ось Земли ( PNPS ). Истинные (географические) меридианы – линии (окружности), образующиеся на поверхности эллипсоида при пересечении его плоскостями истинных меридианов. Меридиан, проходящий через место наблюдателя, принято называть истинным (географическим) меридианом наблюдателя. Начальный (нулевой, Гринвичс-кий) меридиан (*). По Международному Соглашению с 1884 г. за начальный (нулевой) меридиан принят меридиан Гринвича – меридиан, проходивший через ось главного телескопа прежней Гринвичской обсерватории в предместье г. Лондона (Англия). географические координа-ты: географическая широта (параллель); географическая долгота (меридиан): Примечание: (*) Нулевой (Гринвичский) меридиан делит земной шар на восточное и западное полушария.

P N

C

W

Б

E

E

Q

О

А

С *

P S

Географические координаты

Наблюдатель «Б»

нормаль

нормаль

Наблюдателя «А»

В системе географических координат, координат-ными осями являются: земной экватор; начальный (Гринвичский) меридиан. Координатами в геог-рафической системе координат являются: географическая широта –  ( Ш );

географическая долгота –  ( Д ).

Географическая широта – угол при центре Земли между плоскостью экватора и нормалью к поверхности земного эллипсоида в данной точке. Этот угол измеряется дугой меридиана от экватора до параллели данной точки.

Географическую широту обозначают символом «  » (фи) или « Ш ». Счет широты ведется от экватора к северному ( PN ) или южному ( PS ) полюсам. Предел изменения широты от 0  до 90  (на эквато-ре  = 0  , на полюсах  = 90  ). Если точка (т. А ) находится в северном полушарии, то широте дается наименование северная (нордовая) и обозначается буквой N ( С ); а при вычислениях северная или нордовая широта имеет знак «+». Если же точка (т. Б ) находится в южном полушарии, то широте дается наименование южная (зюйдовая) и обозначается буквой S ( Ю ), а при вычислениях южная или зюйдовая широта имеет знак «–».

Все точки, расположенные на одной параллели имеют одинаковую широту (  А =  А  =  А  и  Б =  Б  =  Б  ).

P N

А /

А

А //

0

Е

(+)

Q

Б /

(-)

Б

Б //

Б

P S

Географическая долгота – двугранный угол между плоскостью Гринвичского (начального) меридиана и плоскостью меридиана данной точки. Этот двугранный угол измеряется сфери-ческим углом при полюсе между указанными меридианами или же – географическая долгота измеряется меньшей дугой экватора от Грин-вичского меридиана до меридиана данной точки.

Географическую долготу обозначают буквой «  » (лямбда) или « Д ». Счет долгот ведется от нуле-вого (Гринвичского) меридиана к востоку (к исту ) и западу ( весту ). Пределы изменения долготы от 0  до 180  . Если точка (т. А ) находится в восточном (истовом) полушарии, то ее долготе дается наименование восточная (истовая) и обозначается буквой Е (ист), а при вычислениях ей приписывается знак «+».

Если же точка (т. Б ) находится в западном полушарии, то ее долготе дается наименование западная (вестовая) и обозначается буквой W (вест), а при вычислениях ей приписывается знак «–».

Все точки, находящиеся на одной и той же половине меридиана имеют одну и ту же долготу (  А =  А  =  А  ;  Б =  Б  =  Б  ). Долготы точек, находящихся на противоположной стороне этого меридиана, отличаются от первых на 180  .

Нулевой

(начальный

Гринвичский

меридиан

P N

Б ”

А

А ’

Е

O

Q

(-)

(+)

W

E

Б

Восточноеполушарие

Западное полушарие

Б

А ”

Б ’

P S

Нулевой меридиан

Судно №2

Судно №1

Экватор

Величинами, характеризующими изменение географических координат при переходе судна от одной точки к другой, являются разность широт и разность долгот.

Пункт (т. А или т. А  ), откуда вышло судно, называ-ется пунктом отхода . Пункт отхода характе-ризуется начальными координатами (  1,  1 или  1  ,  1  ). Пункт (т. Б или т. Б  ), в который пришло судно, называется пунктом прихода.

Пункт прихода характеризуется конечными коор-динатами (  2,  2 или  2  ,  2  ). Тогда:– изменение широты (  ), при переходе судна из одного пункта в другой будет называться разностью широт и сокращенно обозначается как   – основное обозначение или как РШ – запасное обозначение. Разность широт (   ) измеряется отрезком дуги (меньшей дуги) меридиана между параллелями пунктов отхода и прихода. – формула алгебраическая. Если судно перемещается в направлении северного полюса PN (судно № 2), то разности широт (   ) дается наименование «к северу» («к норду»), и обозначается – к N , а при вычислениях ей приписывается знак «+».

Разности широт и долгот

P N

А

РШ к S( - )

Б

0

E

Q

РД

Б /

РШ / к N (+)

А /

P S

Пример:  1  = 75  00,0  S ,  2  = 25  00,0  S (судно № 2), тогда:

РШ  (   ) =  2  –  1  = –25  00,0  – (–75  00,0  ) = +50  00,0  или 50  00,0  к N .

Если же судно перемещается в направлении южного полюса PS (судно № 1), то разности широт (   ) дается наименование «к югу» («к зюйду»), и обозначается – к S , а при вычислениях ей приписывается знак « – » .

Пример:  1 = 70  00,0  N ,  2 = 45  00,0  N (судно № 1), тогда:

РШ (   ) =  2 –  1 = 45  00,0  – (+70  00,0  ) = – 25  00,0  или 25  00,0  к S .

Разность широт измеряется в пределах от 0  до  180  (к N или к S ).

Разностью долгот называется изменение долготы (  ) при переходе судна из одного пункта в другой и сокращенно обозначается как   – основное обозначение, или как РД – запасное обозначение. Разность долгот (   ) измеряется меньшей дугой экватора, заключенной между меридианами пунктов отхода и прихода.

– формула алгебраическая. Если судно перемещается к востоку (восточная долгота увеличивается, западная долгота уменьшается), то разности долгот дается наименование «к востоку» («к исту») , и обозначается – к Е , а при вычислениях ей приписывается знак « + » .

Пример :  1 = 85  00,0  Е ,  2 = 130  00,0  Е (рис. 1.4 оба судна), тогда:

( РД )   =  2 –  1 = 130  00,0  – (+85  00,0  ) = + 45  00,0  или 45  00,0  к Е .

Если же судно перемещается к западу (восточная долгота уменьшается, западная долгота увеличивается), то разности долгот дается наименование «к западу» («к весту») , и обозначается – к W , а при вычислениях ей приписывается знак «–» .

Пример:  1 = 130  00,0  Е ,  2 = 85  00,0  Е (обратный переход судов 1, 2 из т. Б (т. Б  ) в т. А ( А  ).

( РД )   =  2 –  1 = 85  00,0  – (+130  00,0  ) = –45  00,0  или 45  00,0  к W .

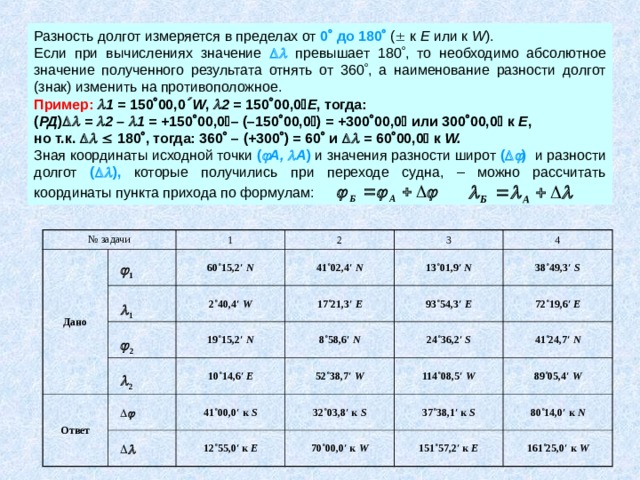
Разность долгот измеряется в пределах от 0  до 180  (  к Е или к W ).

Если при вычислениях значение   превышает 180  , то необходимо абсолютное значение полученного результата отнять от 360  , а наименование разности долгот (знак) изменить на противоположное.

Пример:  1 = 150  00,0  W ,  2 = 150  00,0  Е , тогда:

( РД )   =  2 –  1 = +150  00,0  – (–150  00,0  ) = +300  00,0  или 300  00,0  к Е ,

но т.к.    180  , тогда: 360  – (+300  ) = 60  и   = 60  00,0  к W.

Зная координаты исходной точки (  А,  А ) и значения разности широт (   ) и разности долгот (   ), которые получились при переходе судна, – можно рассчитать координаты пункта прихода по формулам:

№ задачи

Дано

1

2

60˚15,2′ N

2˚40,4′ W

3

41˚02,4′ N

Ответ

17˚21,3′ E

13˚01,9′ N

19˚15,2′ N

4

93˚54,3′ E

10˚14,6′ E

8˚58,6′ N

38˚49,3′ S

24˚36,2′ S

41˚00,0′ к S

52˚38,7′ W

7 2˚19,6′ E

32˚03,8′ к S

12˚55,0′ к E

114˚08,5′ W

41˚24,7′ N

37˚38,1′ к S

70˚00,0′ к W

89˚05,4′ W

151˚57,2′ к E

80˚14,0′ к N

161˚25,0′ к W

Основные линии и плоскости наблюдателя

Отвесная линия

( т. А ) - наблюдатель на Гринвичском (начальном) меридиане.

т. О – центр сферы; линия PNPS – ось Земли, а точки PN и PS – северный и южный географические полюсы.

Через место наблюдателя (т. А ) и центр Земли (т. О ) проведем прямую – отвесную линию ( ZAOn ) , тогда: отвесная линия, проходящая через точку наблюдателя, показывает направления:

а) – над головой наблюдателя – на точку Z – зенит наблюдателя;

б) – в противоположную сторону – на точку n – надир наблюдателя.

Через место наблюдателя (т. А ) перпенди-кулярно отвесной линии ( ZAOn ) проведем плоскость Н-Н  , тогда: горизонтальная плоскость, перпендикулярная направлению отвесной линии и проходящая через место (глаз) наблюдателя называется плоскос-тью истинного горизонта наблюдателя .

Надгоризонтная часть – все, что находится над истинным горизонтом и «видимо» для наблюдателя.

Подгоризонтная часть – все, что находится под истинным горизонтом и «скрыто» от наблюдателя.

Z

W

M

H ’

O

A

S

N

P N

E

H

O

P S

M ’

n

O ’

Отвесная линия

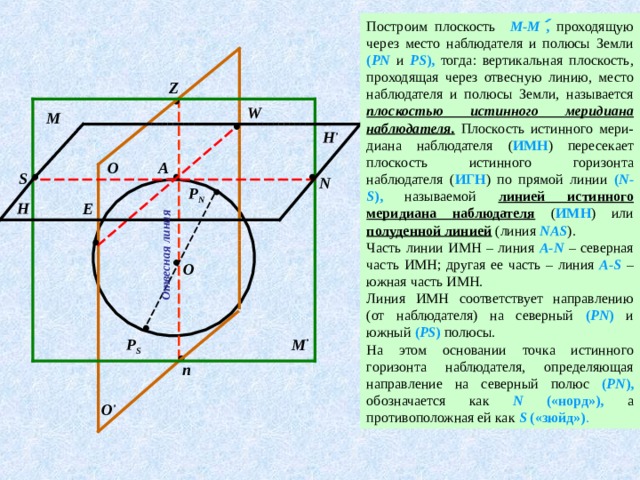
Построим плоскость М-М  , проходящую через место наблюдателя и полюсы Земли ( PN и PS ), тогда: вертикальная плоскость, проходящая через отвесную линию, место наблюдателя и полюсы Земли, называется плоскостью истинного меридиана наблюдателя. Плоскость истинного мери-диана наблюдателя ( ИМН ) пересекает плоскость истинного горизонта наблюдателя ( ИГН ) по прямой линии ( N-S ), называемой линией истинного меридиана наблюдателя ( ИМН ) или полуденной линией (линия NAS ).

Часть линии ИМН – линия А-N – северная часть ИМН; другая ее часть – линия А-S – южная часть ИМН.

Линия ИМН соответствует направлению (от наблюдателя) на северный ( PN ) и южный ( PS ) полюсы.

На этом основании точка истинного горизонта наблюдателя, определяющая направление на северный полюс ( PN ), обозначается как N («норд»), а противоположная ей как S («зюйд») .

Z

W

M

H ’

A

O

S

N

P N

E

H

O

M ’

P S

n

O ’

Отвесная линия

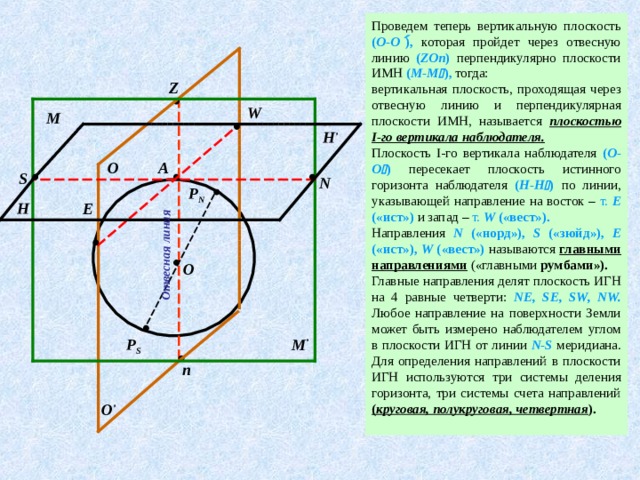
Проведем теперь вертикальную плоскость ( О-О  ), которая пройдет через отвесную линию ( ZOn ) перпендикулярно плоскости ИМН ( М-М  ), тогда:

вертикальная плоскость, проходящая через отвесную линию и перпендикулярная плоскости ИМН, называется плоскостью I-го вертикала наблюдателя.

Плоскость I-го вертикала наблюдателя ( О-О  ) пересекает плоскость истинного горизонта наблюдателя ( Н-Н  ) по линии, указывающей направление на восток – т. Е («ист») и запад – т. W («вест»).

Направления N («норд»), S («зюйд»), Е («ист»), W («вест») называются главными направлениями («главными румбами»).

Главные направления делят плоскость ИГН на 4 равные четверти: NE, SE, SW, NW. Любое направление на поверхности Земли может быть измерено наблюдателем углом в плоскости ИГН от линии N-S меридиана. Для определения направлений в плоскости ИГН используются три системы деления горизонта, три системы счета направлений ( круговая, полукруговая, четвертная ).

Z

W

M

H ’

A

O

S

N

P N

E

H

O

M ’

P S

n

O ’

Системы счета направлений

Круговая система счета

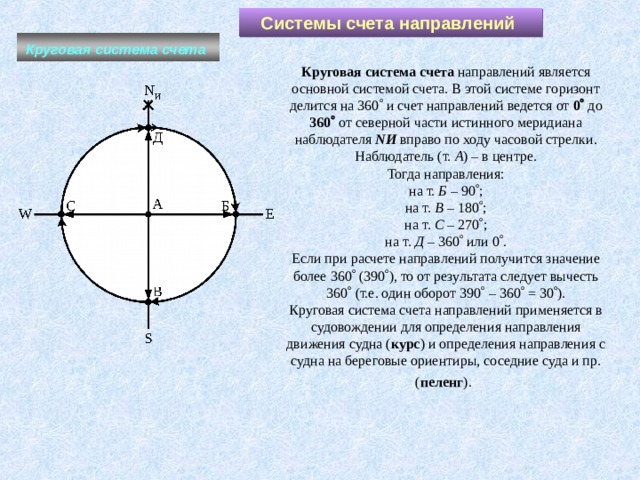
Круговая система счета направлений является основной системой счета. В этой системе горизонт делится на 360  и счет направлений ведется от 0  до 360  от северной части истинного меридиана наблюдателя NИ вправо по ходу часовой стрелки.

Наблюдатель (т. А ) – в центре.

Тогда направления:

на т. Б – 90  ;

на т. В – 180  ;

на т. С – 270  ;

на т. Д – 360  или 0  .

Если при расчете направлений получится значение более 360  (390  ), то от результата следует вычесть 360  (т.е. один оборот 390  – 360  = 30  ).

Круговая система счета направлений применяется в судовождении для определения направления движения судна ( курс ) и определения направления с судна на береговые ориентиры, соседние суда и пр. ( пеленг ).

Полукруговая система счета

В полукруговой системе счета счет направлений ведется от северной или южной части истинного меридиана наблюдате-ля в сторону востока Е или запада W в пределах от 0  до 180  .

Для исключения многозначности в полукруговой системе счета числовому значению направления дается наименование . Например: т.1 N 45  E ; т.2 N 105  W т .3 S 45  W ; т .4 S 135  E

Первая буква наименования – от какой части ИМН ( N или S ) идет счет.

Вторая буква наименования – в каком направлении идет счет (к Е или к W ).

Полукруговая система счета обычно применяется в мореходной астрономии.

Правила перехода от полукруговой системы счета направлений в круговую:

Если наименование N…E  оставь число (45  ) без изменения, отбрось наименование (т. 1).

Если наименование N…W  от 360  вычти число (360  – 105  = 255  , отбрось наименование (т. 2).

Если наименование S…W  к 180  добавь число (180  + 45  = 225  , отбрось наименование (т. 3).

Если наименование S…Е  от 180  вычти число (180  – 135  = 45  , отбрось наименование (т. 4).

Четвертная система счета

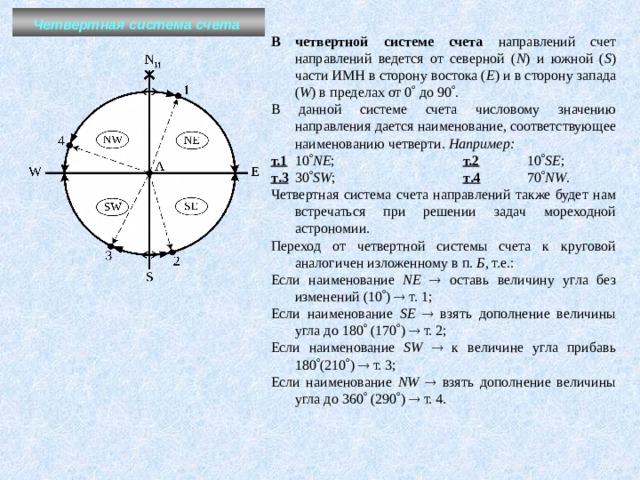
В четвертной системе счета направлений счет направлений ведется от северной ( N ) и южной ( S ) части ИМН в сторону востока ( Е ) и в сторону запада ( W ) в пределах от 0  до 90  .

В данной системе счета числовому значению направления дается наименование, соответствующее наименованию четверти. Например:

т.1 10  NE ; т.2 10  SE ;

т .3 30  SW ; т .4 70  NW .

Четвертная система счета направлений также будет нам встречаться при решении задач мореходной астрономии.

Переход от четвертной системы счета к круговой аналогичен изложенному в п. Б , т.е.:

Если наименование NE  оставь величину угла без изменений (10  )  т. 1;

Если наименование SЕ  взять дополнение величины угла до 180  (170  )  т. 2;

Если наименование SW  к величине угла прибавь 180  (210  )  т. 3;

Если наименование NW  взять дополнение величины угла до 360  (290  )  т. 4.

Румбовая система счета

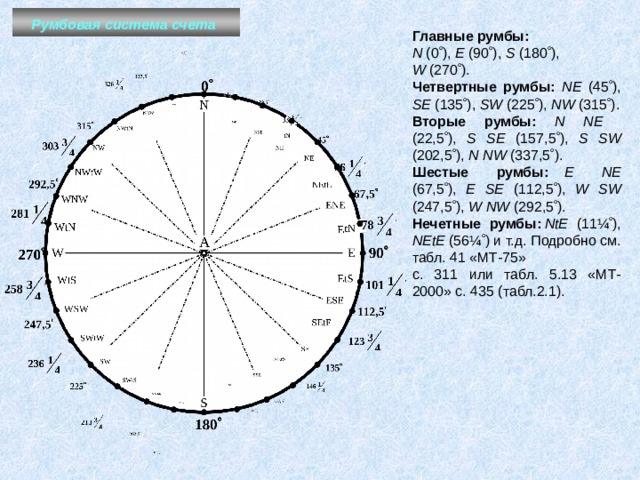
Главные румбы:

N (0  ), E (90  ), S (180  ),

W (270  ).

Четвертные румбы: NЕ (45  ), SE (135  ), SW (225  ), NW (315  ).

Вторые румбы : N N Е (22,5  ), S SE (157,5  ), S SW (202,5  ), N NW (337,5  ).

Шестые румбы : E N Е (67,5  ), E SE (112,5  ), W SW (247,5  ), W NW (292,5  ).

Нечетные румбы: NtE (11¼  ), NEtE (56¼  ) и т.д. Подробно см. табл. 41 «МТ-75»

с. 311 или табл. 5.13 «МТ-2000» с. 435 (табл.2.1).

Носовая часть продольной оси судна

Носовая часть продольной оси судна

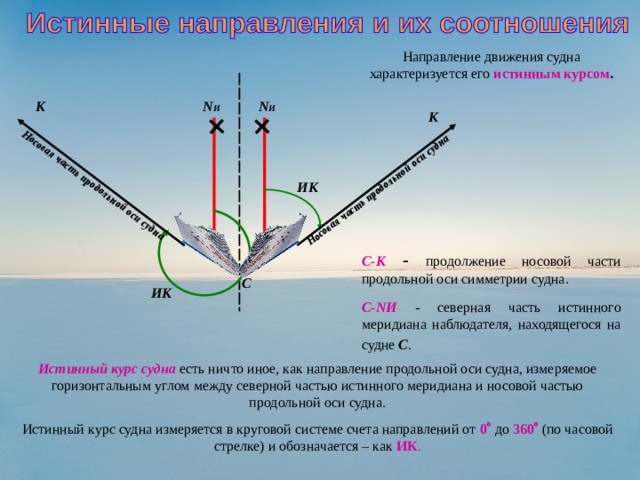
Направление движения судна характеризуется его истинным курсом .

К

N И

N И

К

ИК

С-К - продолжение носовой части продольной оси симметрии судна.

С-NИ - северная часть истинного меридиана наблюдателя, находящегося на судне С .

С

ИК

Истинный курс судна есть ничто иное, как направление продольной оси судна, измеряемое горизонтальным углом между северной частью истинного меридиана и носовой частью продольной оси судна.

Истинный курс судна измеряется в круговой системе счета направлений от 0  до 360  (по часовой стрелке) и обозначается – как ИК .

N И Б

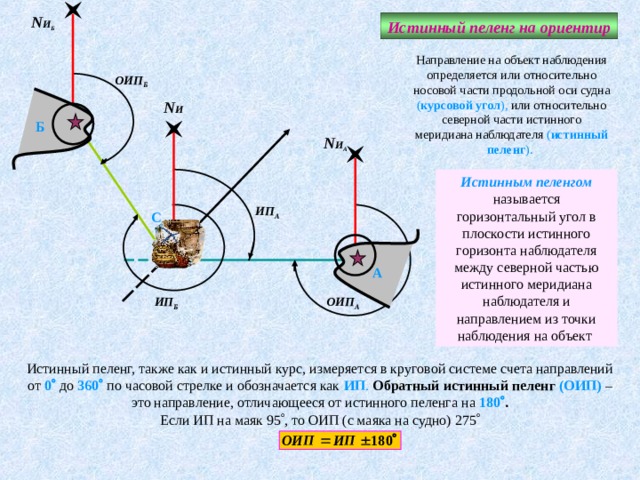
Истинный пеленг на ориентир

Направление на объект наблюдения определяется или относительно носовой части продольной оси судна ( курсовой угол ), или относительно северной части истинного меридиана наблюдателя ( истинный пеленг ).

ОИП Б

N И

Б

N И А

Истинным пеленгом называется горизонтальный угол в плоскости истинного горизонта наблюдателя между северной частью истинного меридиана наблюдателя и направлением из точки наблюдения на объект

ИП А

С

А

ОИП А

ИП Б

Истинный пеленг, также как и истинный курс, измеряется в круговой системе счета направлений от 0  до 360  по часовой стрелке и обозначается как ИП . Обратный истинный пеленг (ОИП) – это направление, отличающееся от истинного пеленга на 180  .

Если ИП на маяк 95  , то ОИП (с маяка на судно) 275 

Курсовой угол

Курсовым углом называется горизон-тальный угол в плоскости истинного горизонта наблюдателя между носовой частью продольной оси судна (ДП судна) и направлением из точки наблюдения на объект (ориентир).

Курсовой угол измеряется в полукруго-вой системе счета направлений от 0  до 180  левого ( л/б ) и правого ( пр/б ) бортов.

Курсовой угол обозначается – как КУ или q .

При вычислениях курсовому углу правого борта ( КУ пр/б ) придается знак «+» , а курсовому углу левого борта ( КУ л/б ) – знак «–» .

Курсовые углы, равные 90  ( 90  пр/б , 90  л/б ) получили название «траверзных» курсовых углов.

Курсовые углы, равные 45  ( 45  пр/б, 45  л/б ) – «крамбола» .

Курсовые углы, равные 135  ( 135  пр/б, 135  л/б ) – «раковина» или «подзор».

0 0

л/б -

пр/б +

180 0

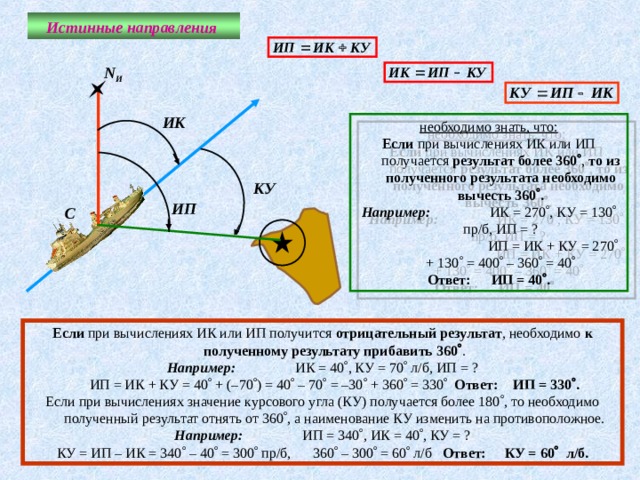
Истинные направления

N И

ИК

необходимо знать, что:

Если при вычислениях ИК или ИП получается результат более 360  , то из полученного результата необходимо вычесть 360  .

Например: ИК = 270  , КУ = 130  пр/б, ИП = ?

ИП = ИК + КУ = 270  + 130  = 400  – 360  = 40 

Ответ: ИП = 40  .

КУ

ИП

С

Если при вычислениях ИК или ИП получится отрицательный результат , необходимо к полученному результату прибавить 360  .

Например: ИК = 40  , КУ = 70  л/б, ИП = ?

ИП = ИК + КУ = 40  + (–70  ) = 40  – 70  = –30  + 360  = 330  Ответ: ИП = 330  .

Если при вычислениях значение курсового угла (КУ) получается более 180  , то необходимо полученный результат отнять от 360  , а наименование КУ изменить на противоположное.

Например: ИП = 340  , ИК = 40  , КУ = ?

КУ = ИП – ИК = 340  – 40  = 300  пр/б, 360  – 300  = 60  л/б Ответ: КУ = 60  л/б.

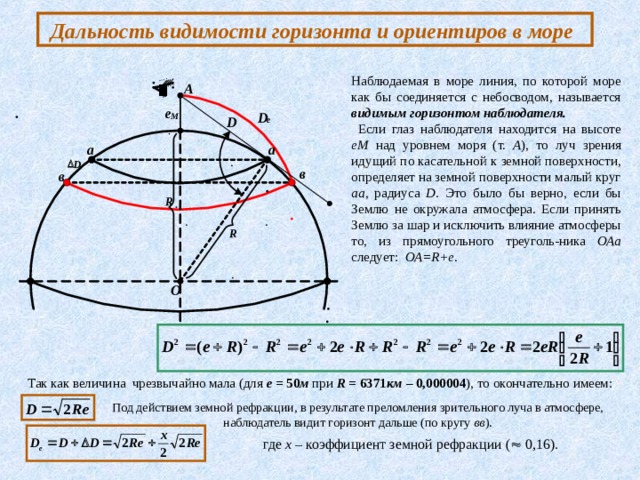
Дальность видимости горизонта и ориентиров в море

Наблюдаемая в море линия, по которой море как бы соединяется с небосводом, называется видимым горизонтом наблюдателя.

Если глаз наблюдателя находится на высоте еМ над уровнем моря (т. А ), то луч зрения идущий по касательной к земной поверхности, определяет на земной поверхности малый круг аа , радиуса D . Это было бы верно, если бы Землю не окружала атмосфера. Если принять Землю за шар и исключить влияние атмосферы то, из прямоугольного треуголь-ника ОАа следует: ОА= R + e .

A

е

D

М

D

e

a

a



D

в

в

R

R

О

Так как величина чрезвычайно мала (для е = 50 м при R = 6371 км – 0,000004 ), то окончательно имеем:

Под действием земной рефракции, в результате преломления зрительного луча в атмосфере, наблюдатель видит горизонт дальше (по кругу вв ).

где х – коэффициент земной рефракции (  0,16).

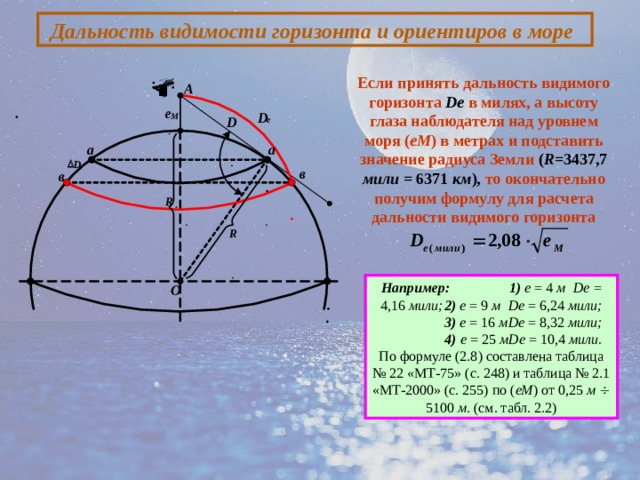
Дальность видимости горизонта и ориентиров в море

Если принять дальность видимого горизонта De в милях, а высоту глаза наблюдателя над уровнем моря ( еМ ) в метрах и подставить значение радиуса Земли ( R =3437,7 мили = 6371 км ), то окончательно получим формулу для расчета дальности видимого горизонта

A

е

D

М

D

e

a

a



D

в

в

R

R

Например: 1) е = 4 м Dе = 4,16 мили; 2) е = 9 м Dе = 6,24 мили;

3) е = 16 м Dе = 8,32 мили; 4) е = 25 м Dе = 10,4 мили.

По формуле (2.8) составлена таблица № 22 «МТ-75» (с. 248) и таблица № 2.1 «МТ-2000» (с. 255) по ( еМ ) от 0,25 м  5100 м . (см. табл. 2.2)

О

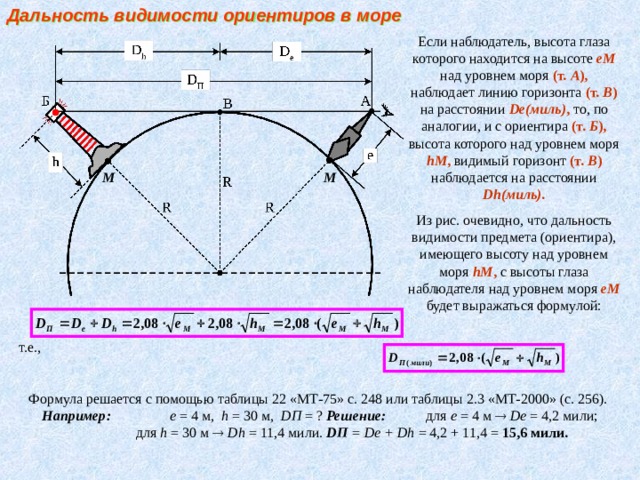
Дальность видимости ориентиров в море

Если наблюдатель, высота глаза которого находится на высоте еМ над уровнем моря (т. А ), наблюдает линию горизонта (т. В ) на расстоянии Dе(миль) , то, по аналогии, и с ориентира (т. Б ), высота которого над уровнем моря hM , видимый горизонт (т. В ) наблюдается на расстоянии Dh(миль) .

Из рис. очевидно, что дальность видимости предмета (ориентира), имеющего высоту над уровнем моря hM , с высоты глаза наблюдателя над уровнем моря еМ будет выражаться формулой:

М

М

т.е.,

Формула решается с помощью таблицы 22 «МТ-75» с. 248 или таблицы 2.3 «МТ-2000» (с. 256). Например: е = 4 м, h = 30 м, DП = ? Решение: для е = 4 м  Dе = 4,2 мили;

для h = 30 м  Dh = 11,4 мили. DП = Dе + Dh = 4,2 + 11,4 = 15,6 мили.

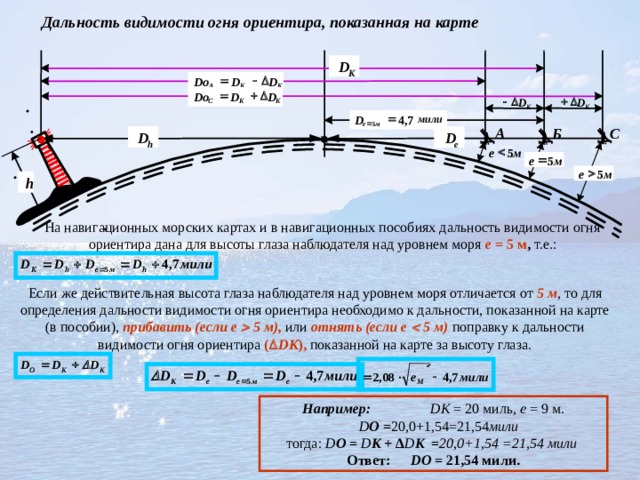
Дальность видимости огня ориентира, показанная на карте

D

К







Do

D

D

A

K

K







D

D

Do









D

D

C

K

K

K

K



4

,

7

D

мили



5

e

м

Б

С

А

D

D

е

h



5

м

e



5

м

e



5

м

e

h

На навигационных морских картах и в навигационных пособиях дальность видимости огня ориентира дана для высоты глаза наблюдателя над уровнем моря е = 5 м , т.е.:

Если же действительная высота глаза наблюдателя над уровнем моря отличается от 5 м , то для определения дальности видимости огня ориентира необходимо к дальности, показанной на карте (в пособии), прибавить (если е  5 м), или отнять (если е  5 м) поправку к дальности видимости огня ориентира (  DК ), показанной на карте за высоту глаза.

Например: DК = 20 миль, е = 9 м.

D О = 20,0+1,54=21,54 мили

тогда: D О = D К + ∆ D К = 20,0+1,54 =21,54 мили

Ответ: DО = 21,54 мили.