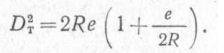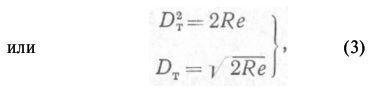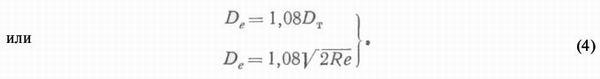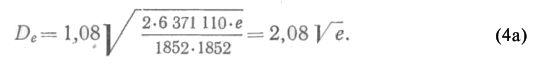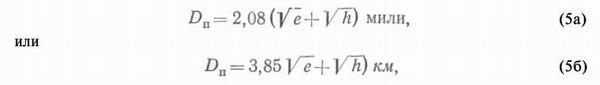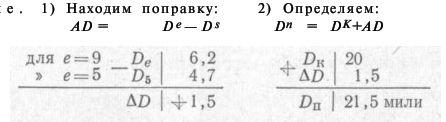Навигация. Основные понятия и определения.

Тема 1.1. Основные понятия и определения.

План лекции №1

1.Форма и размеры Земли.

2.Основные точки, линии и плоскости на Земном шаре.

3.Географические координаты.

4.Морские единицы измерения скорости и пройденного расстояния.

5.Видимый горизонт. Дальность видимого горизонта, объектов и огней.

Цель занятия:

Знать:

- основные точки, линии и плоскости на Земном шаре;

- географические координаты;

- морские единицы измерения скорости и пройденного расстояния;

- видимый горизонт;

- дальность видимости горизонта, объектов и огней.

Уметь:

- определять координаты пунктов прихода;

- определять разность широт и разность долгот;

- определять дальность видимости ориентиров.

1.Форма и размеры Земли.

Вряд ли нужно много писать о форме Земли. Всем ясно, что Земля представляет собой шар, слегка сплюснутый у полюсов, т. е. так называемый эллипсоид. Однако правильное, современное представление о форме и размерах Земли было достигнуто далеко не сразу и достигалось порою в тяжелой борьбе науки с религией.

На протяжении ряда веков, через дебри схоластики и религии средневековья, пробивала себе путь истина.

Однако за последние десятилетия накопился огромный материал; появилась возможность уточнить прежние данные о форме и размерах Земли. К тридцатым годам была выполнена работа по пересмотру всех новых данных, и в 1936 г. советский ученый Ф. Н. Красовский опубликовал новые цифры, характеризующие размеры земного эллипсоида еще точнее.

Эллипсоид Ф. Н. Красовского имеет следующие размеры (рис. 3): большая полуось, т. е. расстояние от центра Земли до экватора, равна 6 378 254 метрам; малая полуось, т. е расстояние от центра Земли до одного из полюсов равна 6 356 863 метрам. Таким образом полярный радиус (от центра к полюсу) короче экваториального радиуса (от центра к экватору) приблизительно на 21 км. Отсюда следует, что Земля действительно эллипсоид вращения, т. е. шар, сплюснутый, хотя и очень незначительно, у полюсов. Величина сжатия, вызванного вращением Земли вокруг своей оси, равна 1 : 298,3. Итак, в первом, и достаточно хорошем, приближении Земля должна быть принята за эллипсоид вращения, элементы которого опубликованы в 1936 г. и которые приняты в Советском Союзе в качестве официальных, т. е. обязательных для использования во всех специальных работах.

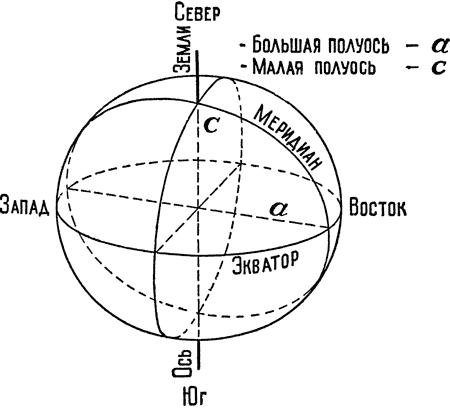
Рис. 3. Земля — эллипсоид вращения;

а — большая полуось; с — малая полуось.

Экваториальный диаметр = 12 756,5 километра Полярный диаметр = 12 713,7 километра Длина окружности меридиана = 40 008,6 километра Длина окружности экватора = 40 075,7 километра Поверхность Земли = 510 миллионам квадратных километров Объем Земли = 1080 миллиардам кубических километров

2.Основные точки, линии и плоскости на Земном шаре.

Ось вращения Земли PNPS пересекается с земной поверхностью в двух точках, которые называются географическими, или истин­ными, полюсами: северным РN (рис. l) и южным Ps. Любая плос­кость, проходящая через ось Земли, называется плоскостью истин­ного меридиана. В пересечении с поверхностью Земли эти плоско­сти образуют меридианы.

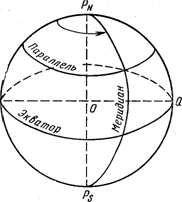
Рис. l. Основные точки и линии земного шара

Плоскость, перпендикулярная оси вращения Земли и проходя­щая через центр Земли, называется плоскостью экватора. В пере­сечении с поверхностью Земли она образует линию экватора EQ. Экватор делит Землю на два полушария — северное и южное.

Плоскости, параллельные плоскости экватора, при пересечении земной поверхности образуют малые круги, называемые паралле­лями. Все меридианы и параллели пересекаются под прямыми уг­лами.

Представим себе наблюдателя, находящегося на земной поверх­ности в точке А (рис. 2). Отвесная линия zА, проходящая через место наблюдателя, указывает направление zn (зенит—надир).

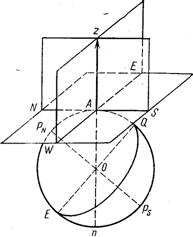Рис.2. Плоскости и линии наблюдателя

Плоскость, проходящая через точку А и перпендикулярная от­весной линии zn, называется плоскостью истинного горизонта на­блюдателя.

Любая плоскость, проходящая через отвесную линию, будет вер­тикальной плоскостью. Вертикальная плоскость, проходящая через место наблюдателя и земные полосы pn и ps, называется плос­костью истинного меридиана наблюдателя. В пересечении с плос­костью истинного горизонта она образует направление N — S.

Вертикальная плоскость, проходящая через точку наблюдателя и перпендикулярная плоскости истинного меридиана наблюдателя, называется плоскостью первого вертикала. В пересечении с плос­костью истинного горизонта плоскость первого вертикала образует линию Е — W.

3.Географические координаты.

Для определения положения какой-либо точки на поверхности Земли применяют географические координаты — широту и долготу.

Географической широтой называется центральный угол между отвесной линией точки А (рис. 3) и ее проекцией на плоскость экватора. Широта измеряется дугой меридиана, заключенной меж­ду экватором и параллелью данной точки к N или к S от 0° до 90°. Широта может иметь наименование северной (нордовой) N или южной (зюйдовой) S.

Географической долготой называется двугранный угол, заклю­ченный между плоскостью начального меридиана (Гринвичского) и плоскостью меридиана, проходящего через данную точку А.

Долгота измеряется дугой экватора от начального меридиана до меридиана данной точки от 0° до 180° к востоку или к западу. Относительно начального меридиана долгота имеет наименование восточной (Е) или западной (W).

Условно географической северной широте и восточной долготе приписывается знак (+). Географической южной широте и запад­ной долготе приписывается знак минус (—). Географическая ши­рота обозначается греческой буквой φ, а долгота — греческой бук­вой λ.

Совершая плавание из одной точки в другую, судно непрерывно меняет широту и долготу.

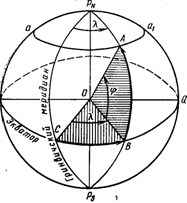
Рис.3. Географические координаты- широта и долгота:

EQ-экватор; aa₁-парралель; О- центр Земли; С и В – точки пересечения Гринвического меридиана и меридиана данной точки А

Допустим, что координаты пункта отхода А будут φ1 и λ1, а координаты пункта прихода В—φ2 и λ2 (рис. 4). Изменения широты и долготы называются соответственно разностью широт (РШ) и разностью долгот (РД).

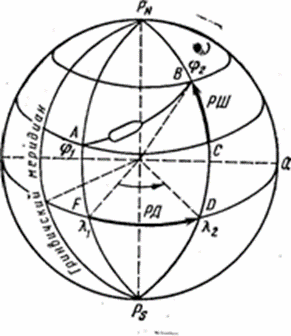
Рис. 4. Разность широт и разность долгот

Разность широт измеряется дугой меридиана от параллели точ­ки отшествия (А) до параллели точки пришествия (В):

РШ φ2-φ1

Разность широт измеряется от 0° до 180° к северу (норду) или к югу (зюйду) и имеет наименование «к N»—знак плюс (+) или «к S» — знак минус (—).

Задачи та определение РШ удобно решать со знаками, контро­лируя решение вспомогательным чертежом.

Можно решать задачи по нахождению широты точек А или В, если известна РШ:

φ1=φ2-РШ; φ2=φ1+РШ.

Эти формулы алгебраические.

Разность долгот (РД) измеряется наименьшей дугой экватора, заключенной между меридианом точки отшествия и меридианом точки пришествия. Разность долгот измеряется от 0° до 180° к во­стоку Е или к западу (W).

Разности долгот условно присваивается знак плюс (+), если она сделана к востоку, и знак минус (—), если к западу.

Алгебраическая формула разности долгот следующая:

РД=λ2-λ1.

Контролировать правильность решения можно вспомогательным чертежом.

Если РД, рассчитанная по формуле, получилась больше 180°, нужно взять дополнение до 360° и изменить наименование РД на обратное.

4.Морские единицы измерения скорости и пройденного расстояния.

Единицей измерения расстояний на море является морская миля, равная линейной длине 1' дуги меридиана земного шара, т. е. 1852 м 66070 фут. Кроме морской мили, для измерения расстояния на море приняты также следующие единицы длины: 

Скорость морского судна измеряют узлами , т. е. количеством морских миль, которое оно проходит за 1 ч. Говорят, например, что судно имеет скорость 12 узлов, т. е. оно проходит 12 морских миль в час. 

При плавании по внутренним водным путям часто применяют метрические единицы измерения расстояния и скорости. Перевод морских миль в километры и обратно осуществляется по следующим формулам: 

S км= 1,852 морских миль; 5 морских миль = 0,54 км. 

По аналогичным формулам делают перевод узлов в км/ч, в м/сек и обратно: 

V км/ч =.1,852 узлов; V узлов = 0,5400 км/ч; 

V м/сек — 0,5145 узлов; V узлов = 1,943 м/сек. 

В Мореходных таблицах МТ-63 помещены сравнительные таблицы скоростей (табл. № 37), облегчающие указанный перевод. 

5.Видимый горизонт. Дальность видимого горизонта, объектов и огней.

Видимый горизонт, в отличие от истинного горизонта, представляет собой окружность, образованную точками касания лучей, проходящих через глаз наблюдателя касательно к земной поверхности. Представим, что глаз наблюдателя (рис. 8) находится в точке А на высоте ВА=е над уровнем моря. Из точки А можно провести бесчисленное количество лучей Ac, Ac¹, Ас², Ас³ и т. д., касательных к поверхности Земли. Точки касания с, с¹ с² и с³ образуют окружность малого круга. 

Сферический радиус Вс малого круга с с¹с²с³ называется теоретической дальностью видимого горизонта. 

Величина сферического радиуса находится в зависимости от высоты глаза наблюдателя над уровнем моря. 
Так, если глаз наблюдателя будет находиться в точке A1 на высоте ВА¹ = е¹ над уровнем моря, то и сферический радиус Вс' будет больше сферического радиуса Вс. 
Чтобы определить зависимость между высотой глаза наблюдателя и теоретической дальностью его видимого горизонта, рассмотрим прямоугольный треугольник АОс: 

Ас² = АО² — Ос²; АО = OB + е; OB = R,

тогда АО = R + е; Ос = R. 

Вследствие незначительности высоты глаза наблюдателя над уровнем моря по сравнению с размерами радиуса Земли длину касательной Ас может принять равной величине сферического радиуса Вс и, обозначив теоретическую дальность видимого горизонта через D^T получим 

D^2T = (R + e)² - R² = R² + 2Re + e² — R² = 2Re + e²,

или 

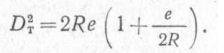
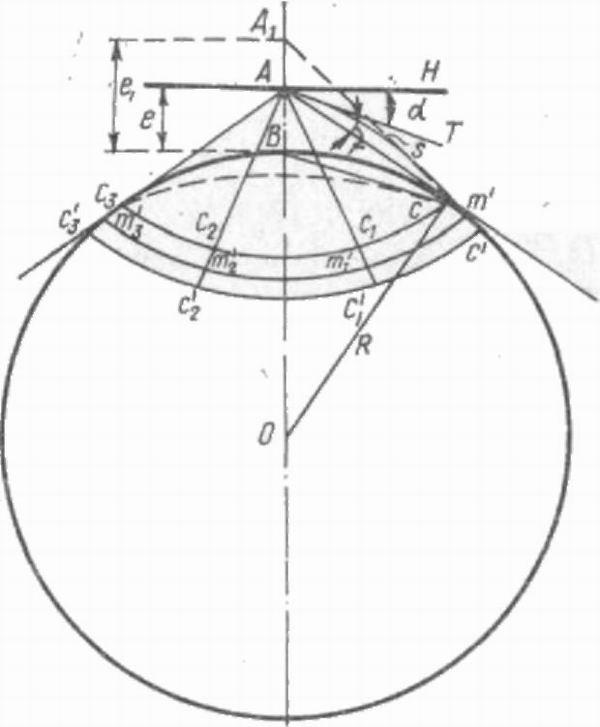
Рис. 8

Учитывая, что высота глаза наблюдателя е на судах не превышает 25 м, a 2R = 12 742 220 м, отношение е/2R настолько мало, что без ущерба для точности им можно пренебречь. Следовательно, 

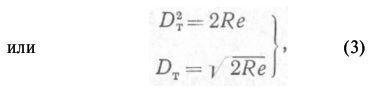
так как е и R выражаются в метрах, то и Dт получится тоже в метрах. Однако действительная дальность видимого горизонта всегда больше теоретической, так как луч, идущий от глаза наблюдателя к точке, находящейся на земной поверхности, из-за неодинаковой плотности слоев атмосферы по высоте преломляется. 
В данном случае луч от точки А к с идет не по прямой Ас, а по кривой ASm' (см. рис. 8). Поэтому наблюдателю точка с представляется видимой по направлению касательной AT, т. е. приподнятой на угол r = L ТАс, называемый углом земной рефракции. Угол d = L HAT называют наклонением видимого горизонта. И на самом деле, видимым горизонтом будет являться малый круг m', m'², тз', с несколько большим сферическим радиусом (Bm' Вс). 
Величина угла земной рефракции не является постоянной и зависит от преломляющих свойств атмосферы, которые изменяются от температуры и влажности воздуха, количества в воздухе взвешенных частиц. В зависимости от времени года и даты суток она также изменяется, поэтому действительная дальность видимого горизонта по сравнению с теоретической может увеличиваться до 15%. 
В навигации увеличение действительной дальности видимого горизонта по сравнению с теоретической принимают 8%. 
Поэтому, обозначив действительную, или, как еще ее называют, географическую, дальность видимого горизонта через D^e, получим: 

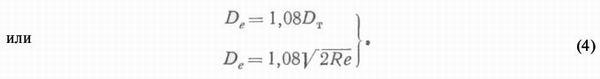
Чтобы получить Dе в морских милях (принимая R и е в метрах), радиус земли R, так же как и высоту глаза е, делим на 1852 (1 морская миля равна 1852 м). Тогда 

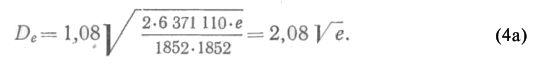
Чтобы получить результат в километрах, вводим множитель 1,852. Тогда 

дл я облегчения расчетов по определению дальности видимого горизонта в табл. 22-а (МТ—63) дана дальность видимого горизонта в зависимости от е, в пределах от 0,25 до 5100 м, рассчитанная по формуле (4а). 

Если действительная высота глаза не совпадает с числовыми значениями, указанными в таблице, то дальность видимого горизонта может быть определена линейным интерполированием между двумя близкими к действительной высоте глаза величинами. 

Дальность видимости предметов и огней

Дальность видимости предмета Dn (рис. 9) будет складываться из двух дальностей видимого горизонта, зависящих от высоты глаза наблюдателя (D^e) и высоты предмета (D^h), т. е. 

Она может быть определена по формуле 

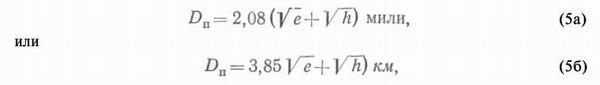
где h — высота ориентира над уровнем воды, м. 

Для облегчения определения дальности видимости предметов пользуются табл. 22-в (МТ—63), рассчитанной по формуле (5а): Чтобы определить по этой таблице, с какого расстояния откроется предмет, необходимо знать высоту глаза наблюдателя над уровнем воды и высоту предмета в метрах. 
Дальность видимости предмета можно также определить по специальной номограмме (рис. 10). Например, высота глаза над уровнем воды 5,5 м, а высота h обстановочного знака 6,5 м, чтобы определить Dⁿ , к номограмме прикладывают линейку так, чтобы она соединяла на крайних шкалах точки, соответствующие h и е. Точка пересечения линейки со средней шкалой номограммы покажет искомую дальность видимости предмета Dⁿ (на рис. 10 Dⁿ = 10,2 мили). 
В пособиях по судовождению — на картах, в лоциях, в описаниях огней и знаков — дальность видимости предметов DK указывается при высоте глаза наблюдателя 5 м (на английских картах — 15 футов). 
В том случае, когда действительная высота глаза наблюдателя другая, необходимо ввести поправку AD (см. рис. 9). 

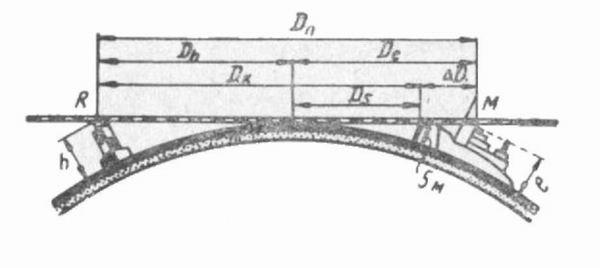
Рис. 9

Пример. Дальность видимости предмета, указанная на карте, DK = 20 милям, а высота глаза наблюдателя е = 9 м. Определить действительную дальность видимости предмета Dⁿ с использованием табл. 22-а (МТ —63). Решение. 

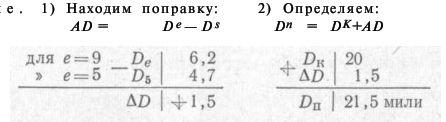
В ночное время дальность видимости огня зависит не только от его высоты над уровнем воды, но также от силы источника освещения и от разряда осветительного аппарата. Обычно осветительный аппарат и сила источника освещения рассчитываются таким образом, чтобы дальность видимости огня ночью соответствовала действительной дальности видимости горизонта с высоты огня над уровнем моря, но бывают и исключения. 
Поэтому огни имеют свою «оптическую» дальность видимости, которая может быть больше или меньше дальности видимости горизонта с высоты огня. 
В пособиях по судовождению указывается действительная (математическая) дальность видимости огней, но если она больше оптической, то указывается последняя. 
Дальность видимости береговых знаков судоходной обстановки зависит не только от состояния атмосферы, но и от многих других факторов, к которым относятся: 
а) топографические (определяются характером окружающей местности, в частности преобладанием того или иного цвета в окружающем ландшафте); 
б) фотометрические (яркость и цвет наблюдаемого знака и фона, на котором он проектируется); 
в) геометрические (расстояние до знака, его размеры и форма). 

Контрольные вопросы:

1. Какова форма Земли?

Дать определение:

2. Экватор -………

3. Меридиан -………

4. Плоскость истинного горизонта наблюдателя - ………

5. Географическая широта - ………

6. Географическая долгота - ………..

7. Формула расчета дальности видимости огней?