
Решение планиметрической задачи при подготовке к ЕГЭ
МБОУ г. Мурманска «Лицей 2»
Кришталь Е.Н.
Мешкова Г.Н.
Лаврухин В.А.

Структурное содержание
а) доказать геометрический факт
б) найти (вычислить) геометрическую величину

Геометрическая конфигурация в пункте а
- подобие указанных треугольников;
- параллельность или перпендикулярность указанных прямых;
- равенство указанных углов, отрезков, площадей или их заданное отношение;
- принадлежность указанной фигуры к определенному типу.

Алгоритм решения задачи
- Чтение условия задачи.
- Выполнение чертежа с буквенными обозначениями.
- Краткая запись условия (база знаний)
- Деталировка – вычерчивания отдельных деталей на дополнительных чертежах
- Составление цепочки действий
- Реализация алгоритма решения
- Проверка правильности решения (логику доказательства, найденные величины имеют геометрический смысл)

Критерии оценивания задания
Содержание критерия, задание №16
Баллы
Имеется верное доказательство утверждения пункта а и обоснованно получен верный ответ в пункте б
3
Обоснованно получен верный ответ в пункте б ИЛИ
имеется верное доказательство утверждения пункта а и при обоснованном решении пункта б получен неверный ответ из-за арифметической ошибки
2
Имеется верное доказательство утверждения пункта а, ИЛИ
при обоснованном решении пункта б получен неверный ответ из-за арифметической ошибки, ИЛИ
1
Решение не соответствует ни одному из критериев, перечисленных выше
обоснованно получен верный ответ в пункте б с использованием утверждения пункта а, при этом пункт а не выполнен
0
Максимальный балл
3
Виды задач
- Многоугольники и их свойства
Окружности и системы окружностей
Окружности и треугольники
Окружности и четырёхугольники

Методика подготовки
- Сначала – теория! Учите наизусть.
- Лучшая тренировка на этом этапе — задания из первой части.
- « домашние заготовки» - полезные факты, которые мы учимся доказывать задолго до экзамена.
- многие задачи по планиметрии строятся по одной из так называемых классических схем. Учите их наизусть!
- теоремы, которые входят в школьную программу, но не в явном виде, а как вспомогательные задачи тоже надо знать наизусть!

Методика подготовки
- Помните, что пункт (а) часто содержит подсказку, идею для решения пункта (б).
- Часто работающий приём. Бывает, что в задаче значимые отрезки пересекаются буквой Ж. Или буквой Х. Хорошо, если мы можем перестроим это Ж или Х в треугольник. Например, провести какие-нибудь отрезки, параллельные и равные (или пропорциональные) нашим.
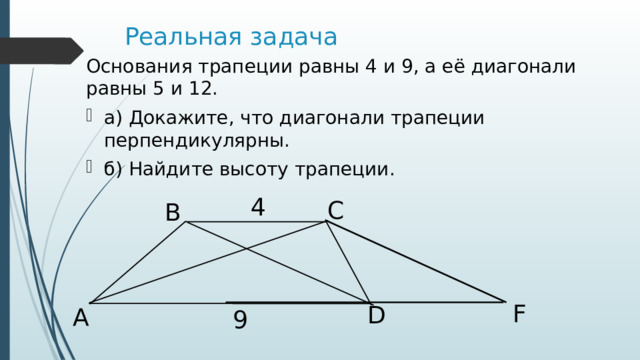
Реальная задача
Oснования трапеции равны 4 и 9, а её диагонали равны 5 и 12.
- а) Докажите, что диагонали трапеции перпендикулярны.
- б) Найдите высоту трапеции.
4
C
B
F
D
A
9

Классические схемы
- В треугольнике проведены высоты
- Окружность и две секущие
- Произвольные треугольники с общей стороной
- Прямоугольные треугольники с общей стороной
- Лемма о трезубце
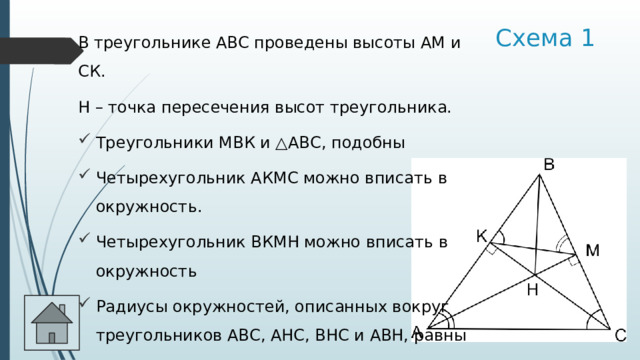
Схема 1
В треугольнике АВС проведены высоты АМ и СК.
H – точка пересечения высот треугольника.
- Треугольники МВК и △АВС, подобны
- Четырехугольник АКМС можно вписать в окружность.
- Четырехугольник ВКМН можно вписать в окружность
- Радиусы окружностей, описанных вокруг треугольников АВС, АНС, ВНС и АВН, равны
 МВ, МD МС. Тогда треугольники ВМС и DМА подобны. " width="640"
МВ, МD МС. Тогда треугольники ВМС и DМА подобны. " width="640"
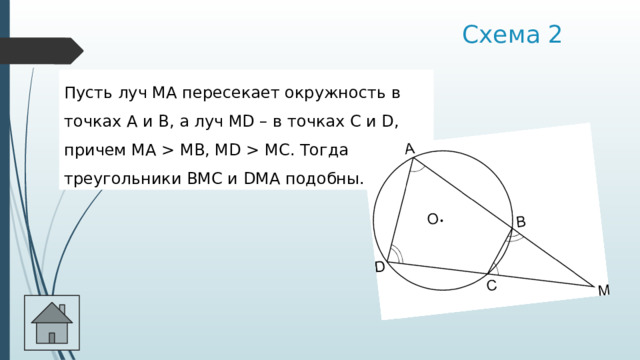
Схема 2
Пусть луч МА пересекает окружность в точках А и В, а луч МD – в точках С и D, причем МА МВ, МD МС. Тогда треугольники ВМС и DМА подобны.

Схема 3
У треугольников АВС и АМС сторона АС – общая, угол В равен углу М, причем точки В и М лежат по одну сторону от прямой АС. Тогда точки А, В, С, М лежат на одной окружности.
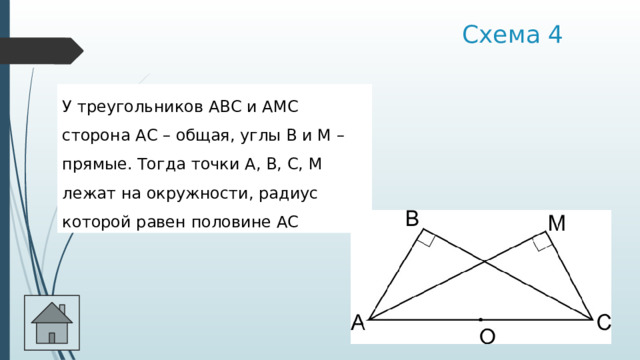
Схема 4
У треугольников АВС и АМС сторона АС – общая, углы В и М – прямые. Тогда точки А, В, С, М лежат на окружности, радиус которой равен половине АС
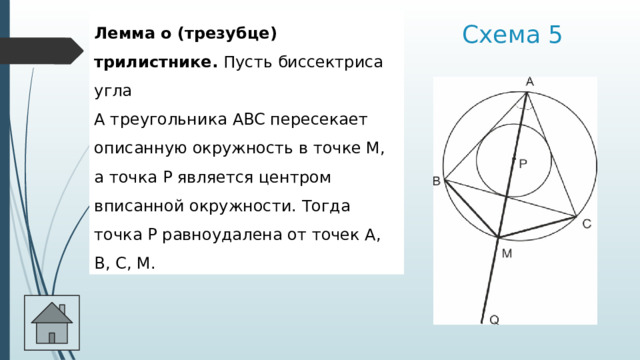
Лемма о (трезубце) трилистнике. Пусть биссектриса угла A треугольника ABC пересекает описанную окружность в точке M, а точка P является центром вписанной окружности. Тогда точка Р равноудалена от точек А, В, С, М.
Схема 5

Задачи для самостоятельного решения
У вас всё получится! Успеха!
![источники ЕГЭ 2019. Математика. Решение задач 16 (профильный уровень). – М.: МЦНМО, 2019 ЕГЭ 2019. Математика. Геометрия. Планиметрия. Задача 16 (профильный уровень) / Под ред. И. В. Ященко. — М.: МЦНМО, 2019. Задания № 16. ЕГЭ. (Математика. 50 вариантов типовых тестовых заданий; под ред. И.В. Ященко. М.: Издательство «Экзамен» Решение планиметрической задачи при подготовке к ЕГЭ. Кривцова С.А. Эл.ресурс [https://4ege.ru/matematika/59758-reshenie-planimetricheskoj-zadachi-pri-podgotovke-k-egje.html] https://ege-study.ru/zadanie-16-profilnogo-ege-po-matematike-planimetriya-zadacha-3/](https://fsd.multiurok.ru/html/2021/12/14/s_61b867f922831/img16.jpg)
источники
- ЕГЭ 2019. Математика. Решение задач 16 (профильный уровень). – М.: МЦНМО, 2019
- ЕГЭ 2019. Математика. Геометрия. Планиметрия. Задача 16 (профильный уровень) / Под ред. И. В. Ященко. — М.: МЦНМО, 2019.
- Задания № 16. ЕГЭ. (Математика. 50 вариантов типовых тестовых заданий; под ред. И.В. Ященко. М.: Издательство «Экзамен»
- Решение планиметрической задачи при подготовке к ЕГЭ. Кривцова С.А. Эл.ресурс [https://4ege.ru/matematika/59758-reshenie-planimetricheskoj-zadachi-pri-podgotovke-k-egje.html]
- https://ege-study.ru/zadanie-16-profilnogo-ege-po-matematike-planimetriya-zadacha-3/


















 МВ, МD МС. Тогда треугольники ВМС и DМА подобны. " width="640"
МВ, МD МС. Тогда треугольники ВМС и DМА подобны. " width="640"




![источники ЕГЭ 2019. Математика. Решение задач 16 (профильный уровень). – М.: МЦНМО, 2019 ЕГЭ 2019. Математика. Геометрия. Планиметрия. Задача 16 (профильный уровень) / Под ред. И. В. Ященко. — М.: МЦНМО, 2019. Задания № 16. ЕГЭ. (Математика. 50 вариантов типовых тестовых заданий; под ред. И.В. Ященко. М.: Издательство «Экзамен» Решение планиметрической задачи при подготовке к ЕГЭ. Кривцова С.А. Эл.ресурс [https://4ege.ru/matematika/59758-reshenie-planimetricheskoj-zadachi-pri-podgotovke-k-egje.html] https://ege-study.ru/zadanie-16-profilnogo-ege-po-matematike-planimetriya-zadacha-3/](https://fsd.multiurok.ru/html/2021/12/14/s_61b867f922831/img16.jpg)





















