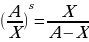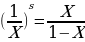Немного о числах Фибоначчи

Немного о числах Фибоначчи

Числа Фибоначчи, их история и связь с «золотым сечением»

Ряд Фибоначчи мог бы остаться только математическим казусом, если бы не то обстоятельство, что все исследователи золотого деления в растительном и в животном мире, не говоря уже об искусстве, неизменно приходили к этому ряду как арифметическому выражению закона золотого деления. С «золотой пропорцией» тесно связан ряд чисел Фибоначчи 1,1,2,3,5,8,13,21,34,55,89 и т.д. В этом ряде каждое последующее число является суммой двух предыдущих. Через четыре столетия после открытия Фибоначчи ряда чисел И. Кеплер установил, что отношение чисел, стоящих рядом, стремится к числу Ф. Эта особенность присуща не только числам из ряда Фибоначчи. Начиная с любых двух чисел и строя аддитивный ряд, в котором каждый член равен сумме двух предыдущих (например, ряд 7,2,9,11,20), видно, что отношения двух последовательных членов такого ряда тоже стремится к числу Ф: чем дальше мы продвигаемся от начала ряда, тем лучше будет приближение. Ученые продолжают развивать теорию чисел Фибоначчи и «золотого сечения». Ю. Матиясевич с использованием чисел Фибоначчи решает десятую проблему Гильберта. Даже была создана Математическая Фибоначчи-ассоциация, которая с 1963 года выпускает специальный журнал.

Обобщённые числа Фибоначчи и «золотое сечение»

Ряд Фибоначчи (1, 1, 2, 3, 5, 8) и открытый им же «двоичный» ряд гирь 1, 2, 4, 8, 16... на первый взгляд совершенно разные. Но алгоритмы их построения весьма похожи друг на друга: в первом случае это сумма двух предыдущих чисел 2 = 1 + 1, 3 = 2 + 1, 5 = 3 + 2…, во втором случае каждое число есть сумма предыдущего числа с самим собой 2 = 1 + 1; 4 = 2 + 2... Нельзя ли отыскать общую математическую формулу, из которой получаются и «двоичный» ряд, и ряд Фибоначчи? А может быть, эта формула даст нам новые числовые множества, обладающие какими-то новыми уникальными свойствами?

Действительно, зададимся числовым параметром S, который может принимать любые значения: 0, 1, 2, 3, 4, 5... Рассмотрим числовой ряд, S + 1 первых членов которого – единицы, а каждый из последующих равен сумме двух членов предыдущего и отстоящего от предыдущего на S шагов. Если n-й член этого ряда мы обозначим через 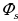 (n), то получим общую формулу:

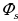 (n) = 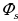(n – 1) +  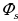(n – S – 1).

Очевидно, что при S = 0 из этой формулы мы получим «двоичный» ряд:

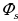 (n) = 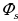(n – 1) +  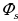(n – 1)

При S = 1 – ряд Фибоначчи:

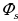 (n) = 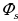(n – 1) +  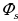(n – 2)

При S = 2, 3, 4. новые ряды чисел, которые получили название S-чисел Фибоначчи.

В общем виде золотая S-пропорция есть положительный корень уравнения золотого S-сечения:

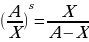
Если целое А принять за единицу, то данное равенство преобразуется в

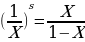
Нетрудно показать, что при S = 0 получается деление отрезка пополам, а при S=1 –знакомое классическое «золотое сечение».

Для удобства повествования четвертой части работы, я представил таблицу корней – Х в зависимости от S, при А=1

Таблица 2,1