Непрерывность функции. Точки разрыва.
Идет бычок, качается, вздыхает на ходу:
– Ох, доска кончается, сейчас я упаду!
На данном уроке мы разберём понятие непрерывности функции, классификацию точек разрыва и распространённую практическую задачу исследования функции на непрерывность. Из самого названия темы многие интуитивно догадываются, о чём пойдёт речь, и думают, что материал довольно простой. Это правда. Но именно несложные задачи чаще всего наказывают за пренебрежение и поверхностный подход к их решению. Поэтому рекомендую очень внимательно прочитать и уловить все тонкости и технические приёмы.
Что нужно знать и уметь? Не очень-то и много. Для качественного усвоения урока необходимо понимать, что такое предел функции.
Понятие непрерывности функции
Рассмотрим некоторую функцию y=f(x) , непрерывную на всей числовой прямой:
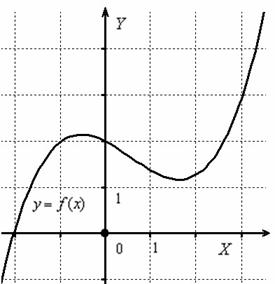
Или, говоря лаконичнее, наша функция непрерывна на R (множестве действительных чисел).
Каков «обывательский» критерий непрерывности? Очевидно, что график непрерывной функции можно начертить, не отрывая карандаша от бумаги.
При этом следует чётко отличать два простых понятия: область определения функции и непрерывность функции. В общем случае это не одно и то же.
Например:
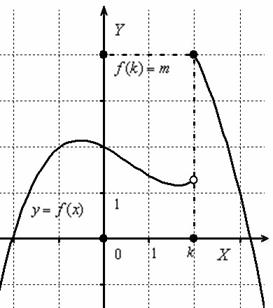
Данная функция определена на всей числовой прямой, то есть для каждого значения «икс» существует своё значение «игрека» y=f(x) . В частности, если x=k , то y=f(k)=m . Заметьте, что другая точка выколота, ведь по определению функции, значению аргумента должно соответствовать единственное значение функции. Таким образом, область определения нашей функции: D(f)=R.
Однако эта функция не является непрерывной на R! Совершенно очевидно, что в точке x=k она терпит разрыв. Термин тоже вполне вразумителен и нагляден, действительно, карандаш здесь по любому придётся оторвать от бумаги.
Непрерывность функции в точке и на интервале
В той или иной математической задаче речь может идти о непрерывности функции в точке, непрерывности функции на интервале, полуинтервале или непрерывности функции на отрезке. То есть, не существует «просто непрерывности» – функция может быть непрерывной ГДЕ-ТО. И основополагающим «кирпичиком» всего остального является непрерывность функции в точке.
С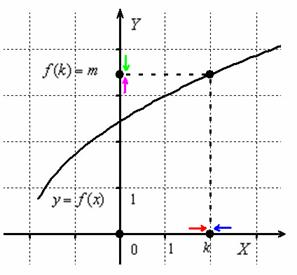 начала введём понятие: односторонние пределы. Рассмотрим будничную ситуацию:
начала введём понятие: односторонние пределы. Рассмотрим будничную ситуацию:
Если приближаться по оси OX к точке k слева (красная стрелка), то соответствующие значения «игреков» будут идти по оси OY к точке m (малиновая стрелка). Математически данный факт фиксируется с помощью левостороннего предела:
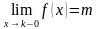
Обратите внимание на запись 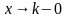 (читается «икс стремится к ка слева»). «Добавка» «минус ноль» символизирует бесконечно малое отрицательное число, по сути это и обозначает, что мы подходим к числу k с левой стороны.
(читается «икс стремится к ка слева»). «Добавка» «минус ноль» символизирует бесконечно малое отрицательное число, по сути это и обозначает, что мы подходим к числу k с левой стороны.
Аналогично, если приближаться к точке «ка» справа (синяя стрелка), то «игреки» придут к тому же значению m , но уже по зелёной стрелке, и правосторонний предел оформится следующим образом: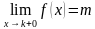
«Добавка» +0 символизирует бесконечно малое положительное число, и запись 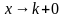 читается так: «икс стремится к ка справа».
читается так: «икс стремится к ка справа».
Если односторонние пределы конечны и равны (как в нашем случае): 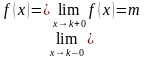 , то будем говорить, что существует ОБЩИЙ предел
, то будем говорить, что существует ОБЩИЙ предел 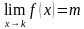 . Всё просто, общий предел – это наш «обычный» предел функции, равный конечному числу.
. Всё просто, общий предел – это наш «обычный» предел функции, равный конечному числу.
Определение: функция непрерывна в точке k, если предел функции в данной точке равен значению функции в этой точке: 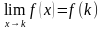 .
.
Определение детализируется в следующих условиях:
1).Функция должна быть определена в точке k, то есть должно существовать значение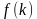 .
.
2). Должен существовать общий предел функции 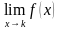 . Как отмечалось выше, это подразумевает существование и равенство односторонних пределов:
. Как отмечалось выше, это подразумевает существование и равенство односторонних пределов: 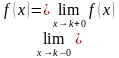 .
.
3). Предел функции в данной точке должен быть равен значению функции в этой точке: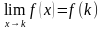 .
.
Если нарушено хотя бы одно из трёх условий, то функция теряет свойство непрерывности в точке k.
Непрерывность функции на интервале формулируется остроумно и очень просто: функция непрерывна на интервале (a;b), если она непрерывна в каждой точке данного интервала.
Классификация точек разрыва
Увлекательная жизнь функций богата всякими особенными точками, и точки разрыва лишь одна из страничек их биографии. Примечание: на всякий случай остановлюсь на элементарном моменте: точка разрыва – это всегда отдельно взятая точка – не бывает «несколько точек разрыва подряд», то есть, нет такого понятия, как «интервал разрывов».
Данные точки в свою очередь подразделяются на две большие группы: разрывы первого рода и разрывы второго рода. У каждого типа разрыва есть свои характерные особенности, которые мы рассмотрим прямо сейчас:
Точка разрыва первого рода
Если в точке k нарушено условие непрерывности и односторонние пределы конечны, то она называется точкой разрыва первого рода.
Изобразим на чертеже график функции 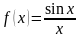
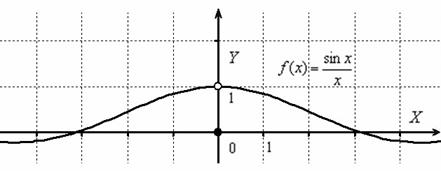
Данная функция непрерывна на всей числовой прямой, кроме точки x=0. И в самом деле, знаменатель же не может быть равен нулю. Однако в соответствии со смыслом предела – мы можем бесконечно близко приближаться к «нулю» и слева и справа, то есть, односторонние пределы существуют и, очевидно, совпадают: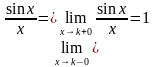
(Условие № 2 непрерывности выполнено).
Но функция не определена в точке x=0, следовательно, нарушено Условие № 1 непрерывности, и функция 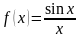 терпит разрыв в данной точке.
терпит разрыв в данной точке.
Разрыв такого вида (с существующим общим пределом) называют устранимым разрывом. Почему устранимым? Потому что функцию можно доопределить в точке разрыва: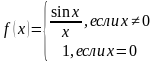
Странно выглядит? Возможно. Но такая запись функции ничему не противоречит! Теперь разрыв устранён и все счастливы:
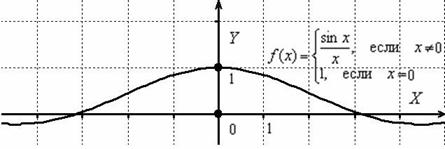
Выполним формальную проверку:
1) f(0)=1– функция определена в данной точке;
2) 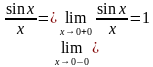 – общий предел существует;
– общий предел существует;
3) 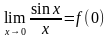 – предел функции в точке равен значению данной функции в данной точке.
– предел функции в точке равен значению данной функции в данной точке.
Таким образом, все три условия выполнены, и функция непрерывна в точке x=0 по определению непрерывности функции в точке.
Рассмотрим кусочную функцию 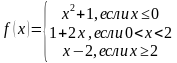 и выполним её чертёж. Как построить график? Очень просто. На полуинтервале
и выполним её чертёж. Как построить график? Очень просто. На полуинтервале  чертим фрагмент параболы
чертим фрагмент параболы 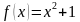 (зеленый цвет), на интервале
(зеленый цвет), на интервале  – отрезок прямой
– отрезок прямой  (красный цвет) и на полуинтервале
(красный цвет) и на полуинтервале  – прямую
– прямую  (синий цвет).
(синий цвет).
При этом в силу неравенства значение f(0) определено для квадратичной функции
значение f(0) определено для квадратичной функции 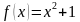 (зелёная точка), и в силу неравенства
(зелёная точка), и в силу неравенства  , значение f(2) определено для линейной функции
, значение f(2) определено для линейной функции  (синяя точка):
(синяя точка):
Сейчас нас будет интересовать только точка x=2. Исследуем её на непрерывность:
1). f(2)=2-2=0 – функция определена в данной точке.
2). Вычислим односторонние пределы.
Слева у нас красный отрезок прямой, поэтому левосторонний предел:
Справа – синяя прямая, и правосторонний предел:
В результате получены конечные числа, причем они не равны. Поскольку односторонние пределы конечны и различны: , то наша функция терпит разрыв первого рода со скачком.
Точки разрыва второго рода
Cамая напрашивающаяся картинка – гипербола в точке ноль. Здесь оба односторонних предела бесконечны: , следовательно, функция терпит разрыв второго рода в точке x=0.
Давайте посмотрим на график функции  , который ещё не встречался:
, который ещё не встречался:
И сследуем на непрерывность точку x=0 по стандартной схеме:
1). Функция не определена в данной точке, поскольку знаменатель обращается в ноль.
Конечно, можно сразу сделать вывод о том, что функция терпит разрыв в точке x=0, но хорошо бы классифицировать характер разрыва, что часто требуется по условию. Для этого:
2). Вычислим односторонние пределы:
Напоминаю, что под записью -0 понимается бесконечно малое отрицательное число, а под записью +0– бесконечно малое положительное число.
Односторонние пределы бесконечны, значит, функция терпит разрыв 2-го рода в точке x=0. Ось ординат является вертикальной асимптотой для графика.
Как исследовать функцию на непрерывность?
Исследование функции на непрерывность в точке проводится по уже накатанной рутинной схеме, которая состоит в проверке трёх условий непрерывности:
Пример 1.
Исследовать функцию  на непрерывность. Определить характер разрывов функции, если они существуют. Выполнить чертёж.
на непрерывность. Определить характер разрывов функции, если они существуют. Выполнить чертёж.
Решение:
1). Под прицел попадает единственная точка x=1, в которой функция не определена.
2). Вычислим односторонние пределы:
Односторонние пределы конечны и равны.
Таким образом, в точке x=1 функция терпит устранимый разрыв.
Как выглядит график данной функции?
Хочется провести упрощение, и вроде бы получается обычная парабола. НО исходная функция не определена в точке x=1, поэтому обязательна следующая оговорка:  , если
, если  .
.
Выполним чертёж:
Ответ: функция непрерывна на всей числовой прямой кроме точки x=1, в которой она терпит устранимый разрыв.
Пример 2.
Исследовать функцию на непрерывность и построить график функции .
Решение: очевидно, что все три части функции непрерывны на соответствующих интервалах, поэтому осталось проверить только две точки «стыка» между кусками. Сначала выполним чертёж на черновике. Единственное, необходимо аккуратно проследить за нашими особенными точками: в силу неравенства  значение
значение  принадлежит прямой
принадлежит прямой  (зелёная точка), и в силу неравенства
(зелёная точка), и в силу неравенства  значение
значение  принадлежит параболе
принадлежит параболе 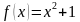 (красная точка):
(красная точка):
Д ля каждой из двух «стыковых» точек стандартно проверяем 3 условия непрерывности:
I). Исследуем на непрерывность точку 
1). f(-1)=-1+2=1 – функция определена в данной точке.
2). Найдём односторонние пределы:
Односторонние пределы конечны и различны, значит, функция  терпит разрыв 1-го рода со скачком в точке
терпит разрыв 1-го рода со скачком в точке  .
.
Вычислим скачок разрыва как разность правого и левого пределов:
, то есть, график рванул на одну единицу вверх.
II). Исследуем на непрерывность точку 
1). f(1)=12+1=2 – функция определена в данной точке.
2). Найдём односторонние пределы:
Односторонние пределы конечны и равны, значит, существует общий предел.
3). – предел функции в точке равен значению данной функции в данной точке.
Таким образом, функция непрерывна в точке  по определению непрерывности функции в точке.
по определению непрерывности функции в точке.
Ответ: функция непрерывна на всей числовой прямой, кроме точки , в которой она терпит разрыв первого рода со скачком.








 начала введём понятие: односторонние пределы. Рассмотрим будничную ситуацию:
начала введём понятие: односторонние пределы. Рассмотрим будничную ситуацию: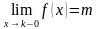
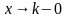 (читается «икс стремится к ка слева»). «Добавка» «минус ноль» символизирует бесконечно малое отрицательное число, по сути это и обозначает, что мы подходим к числу k с левой стороны.
(читается «икс стремится к ка слева»). «Добавка» «минус ноль» символизирует бесконечно малое отрицательное число, по сути это и обозначает, что мы подходим к числу k с левой стороны.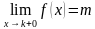
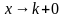 читается так: «икс стремится к ка справа».
читается так: «икс стремится к ка справа».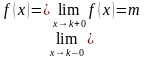 , то будем говорить, что существует ОБЩИЙ предел
, то будем говорить, что существует ОБЩИЙ предел 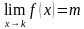 . Всё просто, общий предел – это наш «обычный» предел функции, равный конечному числу.
. Всё просто, общий предел – это наш «обычный» предел функции, равный конечному числу.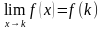 .
.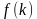 .
.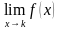 . Как отмечалось выше, это подразумевает существование и равенство односторонних пределов:
. Как отмечалось выше, это подразумевает существование и равенство односторонних пределов: 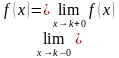 .
.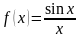

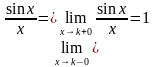
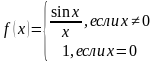

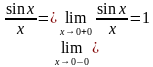 – общий предел существует;
– общий предел существует;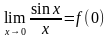 – предел функции в точке равен значению данной функции в данной точке.
– предел функции в точке равен значению данной функции в данной точке.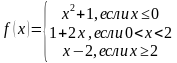 и выполним её чертёж. Как построить график? Очень просто. На полуинтервале
и выполним её чертёж. Как построить график? Очень просто. На полуинтервале  чертим фрагмент параболы
чертим фрагмент параболы 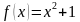 (зеленый цвет), на интервале
(зеленый цвет), на интервале 




















