Нестандартные методы расчета электрических цепей при подготовке к ЕГЭ

Нестандартные методы расчета электрических цепей при подготовке к егэ

Введение

Подготовка к сдаче ЕГЭ по физике является серьезным испытанием для многих школьников. Особенно сложными могут оказаться задачи по расчету электрических цепей, требующие не только знания законов Кирхгофа и правил для расчета сопротивлений, но также умения применять нестандартные методы решения. Использование альтернативных методов при расчете электрических цепей может значительно облегчить процесс подготовки к экзамену и повысить шансы на высокий балл.

Решение задач - неотъемлемая часть обучения физике, поскольку в процессе решения задач формируются физические понятия, развивается физическое мышление учащихся и совершенствуются их навыки применения знаний на практике.

Наряду с этим при решении задач у школьников воспитываются трудолюбие, пытливость ума, смекалка, самостоятельность в суждениях, интерес к учению, воля и характер, упорство в достижении поставленной цели. Для реализации перечисленных целей особенно удобно использовать нетрадиционные задачи.

Задачи по расчету электрических цепей постоянного тока

По школьной программе на рассмотрение данной темы очень мало отводится времени, поэтому учащиеся более или менее успешно овладевают методами решения задач данного типа. Но часто такие типы задач встречаются олимпиадных заданиях, но базируются они на школьном курсе.

К таким, нестандартным задачам по расчету электрических цепей постоянного тока можно отнести задачи, схемы которых:

1) содержат большое число элементов – резисторов или конденсаторов;

2) симметричны;

3) состоят из сложных смешанных соединений элементов.

В общем случае всякую цепь можно рассчитать, используя законы Кирхгофа. Однако эти законы не входят в школьную программу. К тому же, правильно решить систему из большого числа уравнений со многими неизвестными под силу не многим учащимся и этот путь не является лучшим способом тратить время. Поэтому нужно уметь пользоваться методами, позволяющими быстро найти сопротивления и емкости контуров.

Основы расчета электрических цепей для подготовки к ЕГЭ

Основы расчета электрических цепей включают в себя не только классические методы расчета, но и нестандартные подходы, которые могут быть использованы для решения сложных задач. Например, использование метода узлового анализа или метода эквивалентных преобразований позволяет более эффективно решать задачи, требующие комплексного подхода. Эти нестандартные методы могут быть особенно полезны при решении задач на ЕГЭ, где требуется продемонстрировать глубокое понимание основ электротехники и умение применять их на практике.

Нестандартные методы решения задач по электрическим цепям

В контексте задач по электрическим цепям, нестандартные методы решения могут включать применение аналитических методов, например, метода комплексных амплитуд или метода узловых потенциалов, вместо стандартных методов, таких как законы Кирхгофа. Также можно использовать приближенные методы расчетов, в том числе метод Монте-Карло или метод Монте-Карло по моделированию электрических цепей.

Применение метода эквивалентных замен для расчета электрических цепей

Метод эквивалентных замен широко применяется при расчете сложных электрических цепей. Он основан на идее замены сложных участков цепи более простыми элементами, имеющими эквивалентные параметры. Этот метод позволяет упростить расчеты и значительно сократить время, необходимое для нахождения решения. При использовании метода эквивалентных замен важно правильно определить эквивалентные параметры заменяемых участков, такие как сопротивление, сила тока и напряжение.

Метод эквивалентных схем заключается в том, что исходную схему надо представить в виде последовательных участков, на каждом из которых соединение элементов схемы либо последовательно, либо параллельно. Для такого представления схему необходимо упростить. Под упрощением схемы будем понимать соединение или разъединение каких-либо узлов схемы, удаление или добавление резисторов, конденсаторов, добиваясь того, чтобы новая схема из последовательно и параллельно соединенных элементов была эквивалентна исходной.

Эквивалентная схема – это такая схема, что при подаче одинаковых напряжений на исходную и преобразованную схемы, ток в обеих цепях будет одинаков на соответствующих участках. В этом случае все расчеты производятся с преобразованной схемой.

Чтобы начертить эквивалентную схему для цепи со сложным смешанным соединением резисторов можно воспользоваться несколькими приемами. Мы ограничимся рассмотрением в подробностях лишь одного из них – способа эквипотенциальных узлов.

Этот способ заключается в том, что в симметричных схемах отыскиваются точки с равными потенциалами. Эти узлы соединяются между собой, причем, если между этими точками был включен какой-то участок схемы, то его отбрасывают, так как из-за равенства потенциалов на концах ток по нему не течет и этот участок никак не влияет на общее сопротивление схемы.

Таким образом, замена нескольких узлов равных потенциалов приводит к более простой эквивалентной схеме. Но иногда бывает целесообразнее обратная замена одного узла несколькими узлами с равными потенциалами, что не нарушает электрических условий в остальной части.

Рассмотрим примеры решения задач эти методом.

З а д а ч а №1

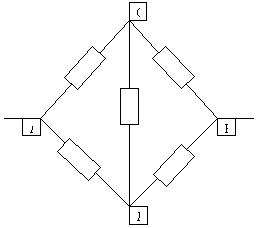
Рассчитать сопротивление между точками А и В данного участка цепи. Все резисторы одинаковы и их сопротивления равны r.

Решение:

В силу симметричности ветвей цепи точки С И Д являются эквипотенциальными. Поэтому резистор между ними мы можем исключить. Эквипотенциальные точки С и Д соединяем в один узел. Получаем очень простую эквивалентную схему:

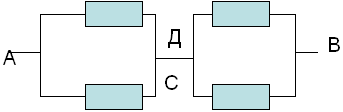
Сопротивление которой равно:

RАВ=Rac+Rcd=r*r/r*r+r*r/r+r=r.

З а д а ч а № 2.

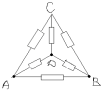
Решение:

Точки С и Д имеют равные потенциалы. Исключением сопротивление между ними. Получаем эквивалентную схему:

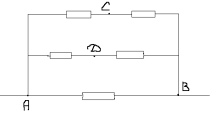
Искомое сопротивление RАВ равно:

1/RАВ=1/2r+1/2r+1/r=2/r

RАВ=r/2.

З а д а ч а № 3.

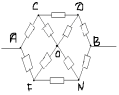
Решение:

Точки C и F-эквивалентные. Соединим их в один узел. Тогда эквивалентная схема будет иметь следующий вид:

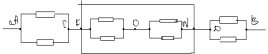
Сопротивление на участке АС:

Rас=r/2

Сопротивление на участке FN:

R_FN =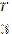 

Сопротивление на участке DB:

R_DB =r/2

Получается эквивалентная схема:

Искомое общее сопротивление равно:

R_AB= r.

З а д а ч а №4

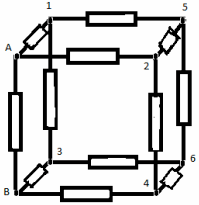
Решение:

Узлы 1 и 2 – эквипотенциальные, поэтому соединим их в один узел I. Узлы 3 и 4 также эквипотенциальные – соединимих в другой узел II. Эквивалентная схема имеет вид:

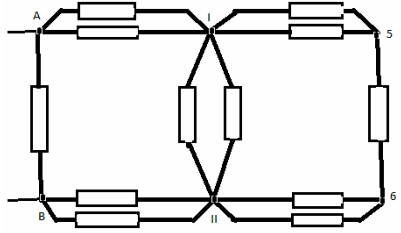
Сопротивление на участке A- I равно сопротивлению на участке B- II и равно:

R_I =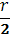

Сопротивление участка I-5-6- II равно:

R_II = 2r

Cопротивление участка I- II равно:

R_III =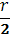 

Получаем окончательную эквивалентную схему:

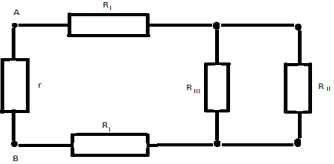
Искомое общее сопротивление цепи R_AB=(7/12)*r.

З а д а ч а № 5

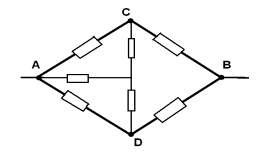
Точки СОD имеют равные потенциалы – соединим их в один узел О^I .Эквивалентная схема изображена на рисунке :

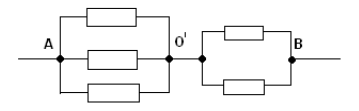
Сопротивление на участке А О^I равно 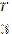  . На участке О^IВ сопротивление равно  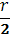 .Получаем совсем простую эквивалентную схему:

ЕЕ сопротивление равно искомому общему сопротивлению

R_AB=(5/6)*r

Обучение решению задач по расчету электрических цепей способом эквипотенциальных узлов

Задача – это проблема, для разрешения которой ученику потребуются логические рассуждения и выводы. Строящиеся на основе законов и методов физики. Таким образом, с помощью задач происходит активизация целенаправленного мышления учащихся.

В то же время. Теоретические знания можно считать усвоенными только тогда, когда они удачно применяются на практике. Задачи по физике описывают часто встречающиеся в жизни и на производстве проблемы, которые могут быть решены с помощью законов физики и, если ученик успешно решает задачи, то можно сказать, что он хорошо знает физику.

Для того, чтобы ученики успешно решали задачи, недостаточно иметь набор методов и способов решения задач, необходимо еще специально учить школьников применению этих способов.

Рассмотрим план решения задач по расчету электрических цепей постоянного тока методом эквипотенциальных узлов.

1. Чтение условия.

2. Краткая запись условия.

3. Перевод в единицы СИ.

4. Анализ схемы:

   1. установить, является ли схема симметричной;

   2. установить точки равного потенциала;

   3. выбрать, что целесообразнее сделать – соединить точки равных потенциалов или же, наоборот, разделить одну точку на несколько точек равных потенциалов;

   4. начертить эквивалентную схему;

   5. найти участки только с последовательным или только с параллельным соединением и рассчитать общее сопротивление на каждом участке по законам последовательного и параллельного соединения;

   6. начертить эквивалентную схему, заменяя участки соответствующими им расчетными сопротивлениями;

   7. пункты 5 и 6 повторять до тех пор, пока не останется одно сопротивление, величина которого и будет решением задачи.

5. Анализ реальности ответа.

Подробнее об анализе схемы

а) установить, является ли схема симметричной.

Определение. Схема симметрична, если одна ее половина является зеркальным отражением другой. Причем симметрия должна быть не только геометрической, но должны быть симметричны и численные значения сопротивлений или конденсаторов.

Примеры:

1)

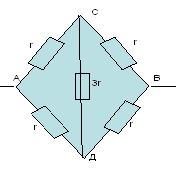
Схема симметричная, так как ветви АСВ и АДВ симметричны геометрически и отношение сопротивления на одном участке АС:АД=1:1 такое же, как и на другом участке СД:ДВ=1:1.

2)

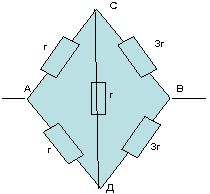
Схема симметричная, так как отношение сопротивлений на участке АС:АД=1:1 такое же, как и на другом участке СВ:ДВ=3:3=1:1

3)

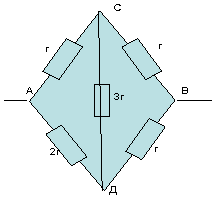
Схема не симметрична, так как отношения сопротивлений численно

не симметричны -1:2 и 1:1.

б) установить точки равных потенциалов.

Пример:

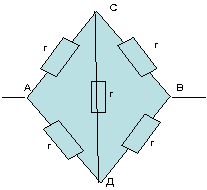
Из соображений симметрии делаем вывод, что в симметричных точках потенциалы равны. В данном случае симметричными точками являются точки С и Д. Таким образом, точки С и Д – эквипотенциальные точки.

в) выбрать, что целесообразно сделать – соединить точки равных потенциалов или же, наоборот, разделить одну точку на несколько точек равных потенциалов.

Мы видим в этом примере, что между точками равных потенциалов С и Д включено сопротивление, по которому ток не будет течь. Следовательно, мы можем отбросить это сопротивление, а точки С и Д соединить в один узел.

г) начертить эквивалентную схему.

Чертим эквивалентную схему. При этом получаем схему с соединенными в одну точку точками С и Д.

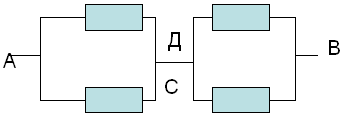
д) найти участки только с последовательным или только с параллельным соединением и рассчитать общее сопротивление на каждом таком участке по законам последовательного и параллельного соединения.

Из полученной эквивалентной схемы видно, что на участке АС мы имеем два параллельно соединенных резистора. Их общее сопротивление находится по закону параллельного соединения:

1/ Rобщ=1/R1+1/R2+1/R3+…

Таким образом 1/RAC=1/r+1/r=2/r, откуда RAC= r/2.

На участке СВ картина аналогичная:

1/RCB= 1/r+1/r =2/r, откуда RCB=r/2.

е)начертить эквивалентную схему, заменяя участки соответствующими им расчетными сопротивлениями.

Чертим эквивалентную схему подставляя в нее рассчитанные сопротивления участков RAC и RCB:

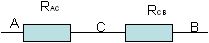
ж)пункты д) и е) повторять до тех пор, пока останется одно сопротивление, величина которого и будет решением задачи.

Повторяем пункт д): на участке АВ имеем два последовательно соединенных сопротивления. Их общее сопротивление находим по закону последовательного соединения:

Rобщ= R1+R2+R3+… то есть, RAB=RAC+RCB = r/2+r/2 =2r/2 = r.

Повторяем пункт е): чертим эквивалентную схему:

Мы получили схему с одним сопротивлением, величина которого равна сопротивлению исходной схемы. Таким образом, мы получили ответ RAB = r.

Использование метода комплексных амплитуд в задачах по электрическим цепям

Метод комплексных амплитуд основан на представлении переменного тока в виде суммы гармонических функций с комплексными амплитудами. Этот метод позволяет упростить расчеты и получить более точные результаты.

При использовании метода комплексных амплитуд нужно учесть, что рассчитываются величины, зависящие от времени, через соответствующие фазы. Например, для определения напряжения или тока в цепи можно использовать комплексное представление этих величин.

При решении задач по электрическим цепям с использованием метода комплексных амплитуд необходимо уметь работать с алгебраическими операциями над комплексными числами и знать основные свойства комплексных амплитуд.

Использование метода комплексных амплитуд позволяет более удобно и эффективно решать задачи по электрическим цепям, особенно в случаях, когда цепь содержит множество элементов или, когда требуются точные результаты

Анализ нестандартных ситуаций в задачах по электрическим цепям при подготовке к ЕГЭ

Анализ нестандартных ситуаций в задачах по электрическим цепям при подготовке к ЕГЭ помогает ученикам развивать навыки самостоятельного мышления и умение применять теоретические знания на практике. Нестандартные ситуации могут включать в себя различные физические условия, отклонения от идеальных параметров элементов цепи или изменение внешних факторов, влияющих на ее работу. В таких задачах требуется применение нестандартных методов расчета, таких как использование неизвестных и переменных, обращение к дополнительным законам Кирхгофа или анализ сложных комбинаций параллельных и последовательных соединений элементов цепи. Такой анализ позволяет ученикам получать более полное представление о работе электрических цепей и повышает их уверенность в решении нестандартных задач на ЕГЭ.