Нестандартные способы решения заданий при подготовке к ГИА. Выступление на РМО.

Математика, которая мне нравится!

Обучение – ремесло, использующее бесчисленное множество маленьких трюков.

Д. Пойа

МБОУ "Ивановская средняя общеобразовательная школа"

Нестандартные способы решения заданий при подготовке к ГИА.

Мы разработали этот шаблон так, чтобы у каждого члена группы проекта был набор слайдов с собственной темой. Чтобы добавить новый слайд в набор, сделайте следующее.

Укажите, куда вы хотите добавить слайд. Для этого в области эскизов выберите существующий слайд, нажмите кнопку «Создать слайд», а затем выберите макет.

У нового слайда будет такая же тема, как и у ранее выбранного.

Будьте осторожны! Не раздражайте выступающих неожиданной сменой темы. Это может случиться, если выбрать вариант темы на вкладке макетов. В этом случае изменится оформление всех слайдов в презентации.

Подготовила: учитель математики первой квалификационной категории МБОУ «Ивановская СОШ» Минаева И. И.

Решение текстовых задач нестандартным способом

Задача на движение

Пароход вниз по течению реки проплыл путь за 2 часа, а вверх против течения

реки за 3 часа. Сколько времени понадобится плоту, чтобы проплыть тот же путь?

• Решение с помощью дробей:
• Примем за 1 весь путь.
• 1:2=1/2 (расстояния)  - часть пути, которую проплывает катер за 1 час по течению;
• 1:3=1/3 (расстояния)  - часть пути, которую проплывает катер за 1 час против течения;
• Так их разница составляет удвоенную скорость течения, то

(1/2 - 1/3):2=1/12 (расстояния)  - часть пути, которую проплывает плот за 1 час.

• 1:1/12=12 (часов)  - время движения плота.

Ответ: 12 ч

• Решение с помощью уравнения:

• Пусть х км/ч – скорость парохода, а

у км/ч скорость течения реки.

• Составим уравнение:

2( х + у ) = 3( х – у )

х = 5у

2( 5у + у ) = 12у

12у(км) – весь путь.

Т.к. у км/ч- скорость течения, то

время равно 12у : у = 12 ( ч )

Ответ: 12 ч

Задача на части

Мама в три раза старше дочери, папа на четыре года старше мамы,

всем вместе 81 год. Сколько лет папе?

Решение:

• Если бы возраст папы был на  4  года меньше,то всем вместе было бы   
•   81 - 4 = 77 лет.
• Если возраст дочери принять за  1  часть, то возраст мамы составит 3 части, папы  3  части, т.е.  77  лет составят 7  частей .

Поэтому

77:7=11(лет)  возраст дочери;

      11· 3=33(года)  маме,

33+4=37 (лет)  папе

Ответ: 37 лет

Задача на пропорции

Бригада студентов из 16 человек за 20 дней собрала 180 тонн картофеля. Сколько картофеля уберет бригада из 12 человек за 28 дней, если будет работать с такой же производительностью?

Решение - рассуждение:

• 1 человек за 20 дней соберет в 16 раз меньше, т.е. 180/16 т;
• 12 человек за 20 дней соберут в 12 раз больше, т.е. (180/16) · 12 т;
• 12 человек за 1 день соберут в 20 раз меньше, т.е. (180·12/16):20 т;
• 12 человек за 28 дней соберут в 28 раз больше, т.е. (180 · 12/16 · 20) · 28 т.
• Результат вычисления: 189 тонн.
• Ответ: 189 тонн.

Решение с помощью пропорции.

16 чел. – за 20 дней – 180 тонн

12 чел. – за 28 дней – X тонн

12 человек за 28 дней собрали 189 тонн картофеля.

Ответ: 189 тонн.

6

Нестандартные способы решения квадратных уравнений.

Свойства коэффициентов

квадратного уравнения

Пусть дано квадратное уравнение ах 2 + bх + с = 0 , где а ≠0 .

Свойство 1

Если а + b + с = 0 (т. е. сумма коэффициентов уравнения равна нулю), то х 1 = 1, х 2 = с/а

Свойство 2

Если а – b + с = 0, или а + с = b, то х 1 = – 1, х 2 = – с/а

6

Закрепление

х 2 + 4х – 5 = 0              

a = 1, b = 4, c = – 5      

a + b + c = 0                  

x 1 = 1, x 2 = – 5                 

           3х 2 +2х – 1 = 0  

       a = 3, b = 2, c = –1

          a + c = b     

  x 1 = – 1, x 2 = 1/3

6

Свойства коэффициентов

квадратного уравнения

Свойство 3

В уравнении вида ах 2 + (а 2 + 1)х + а = 0 х 1 = -а, х 2 = -1/а

Например

а) 6х 2 + 37х + 6 =0           

a = c = 6, b = 37  =  6 2 +1

x 1 = – 6, x 2 = – 1/6      

6

Свойства коэффициентов квадратного уравнения

Свойство 4

В уравнении вида ах 2 - (а 2 + 1)х + а = 0 х 1 = а, х 2 = 1/а

Например

15х 2 - 226х + 15 =0           

a = c = 15, b = -226 = -(15 2 +1)

x 1 = 15, x 2 = 1/15      

Свойства коэффициентов

квадратного уравнения

Свойство 5

В уравнении вида ах 2 + (а 2 - 1)х - а = 0 х 1 = - а, х 2 = 1/а

Например

17х 2 + 288х - 17 =0           

a = 17, c = -а = -17, b = 288  =  17 2 -1

x 1 = – 17, x 2 = 1/17     

Свойства коэффициентов квадратного уравнения

Свойство 6

В уравнении вида ах 2 - (а 2 - 1)х - а = 0 х 1 = а, х 2 = -1/а

Например

г) 10х 2 - 99х - 10 =0           

a = c = 10, b = 99 =  10 2 -1

x 1 = 10, x 2 = – 1/10      

Вычисление площади многоугольника нестандартным способом

6

Формула Пика, или как считать площади многоугольников. (полезно при решении задач в ОГЭ и ЕГЭ)

Формула Пика (теорема Пика)  - классический результат комбинаторной геометрии и геометрии чисел.

Площадь многоугольника с целочисленными вершинами равна

В + Г/2 − 1,

где В есть количество целочисленных точек внутри многоугольника,

а Г   - количество целочисленных точек на границе многоугольника .

В=7 , Г=8 , В + Г/2 − 1= 10

6

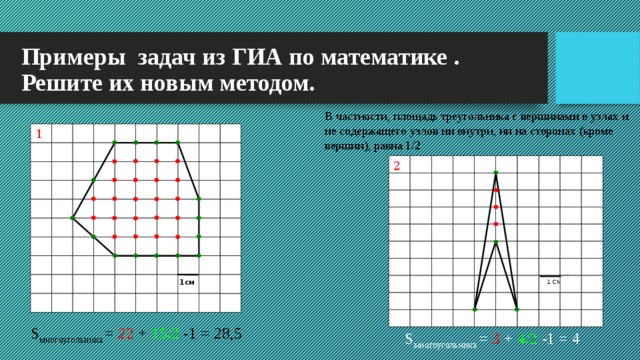
Примеры задач из ГИА по математике . Решите их новым методом.

В частности, площадь треугольника с вершинами в узлах и не содержащего узлов ни внутри, ни на сторонах (кроме вершин), равна 1/2

1

2

1см

1 СМ

1 см

S многоугольника = 22 + 15/2 -1 = 28,5

S многоугольника = 3 + 4/2 -1 = 4

16

Нестандартное решение

стереометрических задач

16

Прямоугольный треугольник и его элементы

Пифагоровы числа

Теорема Пифагора:

с²=а²+ b²

а

b

3

5

4

c

12

8

5

13

15

7

24

17

20

21

12

25

35

29

9

37

40

41

А

с

b

В

С

а

Задачи из ГИА

В правильной четырехугольной пирамиде SABCD точка О – центр основания, S – вершина, SA = 13, BD = 10. Найдите длину отрезка SO.

Решение.

с=13, a=5, b=?

с²=а²+b²

13²=5²+ b²

b²=13²-5², b²=169-25=144, b=12

С

b

a

Ответ: b=12

19

Более сложные задачи ГИА

а

b

3

4

5

c

12

5

8

13

15

7

24

20

17

21

12

25

35

9

29

40

37

41

Решение.

SO=15, SA=25

15

3

25

20

5

4

5

АО=20, значит АС=40

Ответ: 40

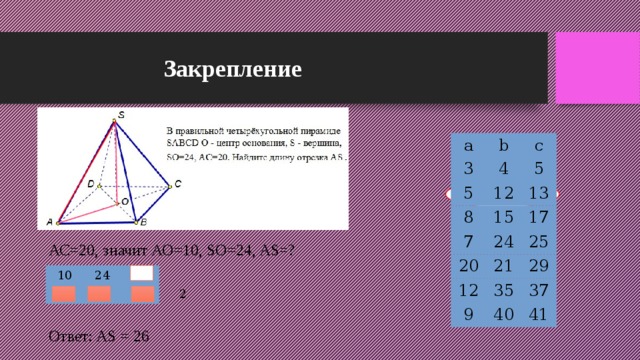
Закрепление

а

b

3

c

4

5

12

8

5

13

15

7

24

17

20

25

21

12

35

9

29

37

40

41

АС=20, значит АО=10, SO=24, AS=?

10

5

24

26

12

13

2

Ответ: AS = 26

Задачи из второй части профильного уровня ЕГЭ

Поэтапно – вычислительный метод

Задача №3. В правильной четырехугольной призме АВСDA 1 B 1 C 1 D 1 стороны основания равны 2, а боковые ребра равны 5. На ребре АА 1 отмечена точка Е так, что АЕ : ЕА 1 = 3 : 2. Найдите угол между плоскостями АВС и ВЕD 1 .

1 способ

D 1

О – точка пересечения прямой ED 1 c плоскостью (АВС).

A 1

АPЕ – линейный угол между плоскостями АВС и ВЕD 1

C 1

2

B 1

E

F

5

3

А

O

D

2

P

C

2

В

Координатный метод

E(2;0;3), B(2;2;0), D 1 (0;0;5),

2x+3y+2z-10=0;

(2;3;2)

В правильной четырехугольной призме АВСDA 1 B 1 C 1 D 1 стороны основания равны 2, а боковые ребра равны 5. На ребре АА 1 отмечена точка Е так, что АЕ : ЕА 1 = 3 : 2. Найдите угол между плоскостями АВС и ВЕD 1 .

2 способ

Решение.

z

D 1

C 1

α : a 1 x + b 1 y + c 1 z + d 1 =0

Вектор нормали плоскости α :

(a 1 ; b 1 ; c 1 )

β : a 2 x + b 2 y + c 2 z + d 2 =0

Вектор нормали плоскости β :

A 1

B 1

(a 2 ; b 2 ; c 2 )

(0; 0;5),

D(0;0;0), D 1 (0;0;5), DD 1 (0; 0;5), т. е.

2

F

E

5

a=c

2a+3c+d=0

5c+d=0

2a+2b+d=0

d=-5c

b=1,5c

D

3

C

y

2

А

2

В

x

24

Спасибо за внимание!

Коллеги, желаю Вам успехов и достижений !

Литература и интернет ресурсы :

1) Интернет ресурсы: Википедия: формула Пика;

2) Открытый банк заданий по математике ОГЭ и ЕГЭ на сайте: mathege.ru и mathgia.ru;