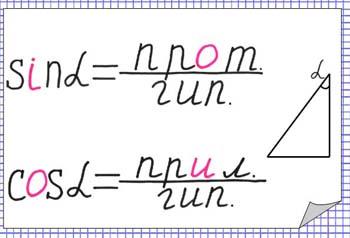Новые приемы эффективного запоминания правил

Седовская общеобразовательная школа

Новые приемы

эффективного

запоминания

правил

Подготовила учитель математики

Швец Елена Георгиевна

Люди получают за свою жизнь огромное количество информации, однако большую часть узнанного забывают. Многие мирятся с этим, считая, что хорошая память (особенно феноменальная) либо есть, либо ее нет. Но оказывается, что это совсем не так.

Существуют новые приемы эффективного запоминания правил посредством создания необычных, нестандартных, ассоциативных, положительных образов, которые можно применять при проведении учебных

занятий по математике в 5-9 классах.

Память можно усовершенствовать, если развивать воображение и творческие способности. Исследования показывают, что работа разных видов памяти подчиняется общим законам. Познакомимся с наиболее важными из них.
Закон осмысления: чем глубже осмысление запоминаемого, тем лучше оно сохраняется в памяти. Для хорошего запоминания удобно использовать ключевые слова, схемы, рисунки и таблицы.
Закон интереса: интересное запоминается легко.
Закон усиления первоначального впечатления: чем ярче первое впечатление от созданного образа, тем прочнее само запоминание.
Для лучшего запоминания с давних пор используются мнемотехнические приемы. Их суть заключается в том, что информация, которую необходимо запомнить, определенным образом структурируется. Например, дату французской революции – 1789 год – легко запомнить, если обратить внимание на последовательность цифр: 7,8,9.
Рассмотрим важнейшие принципы мнемотехники. В основе развитой памяти лежат два основных фактора – воображение и ассоциация. Для того чтобы запомнить что-то новое, вам необходимо соотнести это новое с чем-то, т.е. провести ассоциативную связь с каким-то уже известным фактором, призвав на помощь свое воображение. Ассоциация – это мысленная связь между двумя образами. Чем многообразнее и многочисленнее ассоциации, тем прочнее они закрепляются в памяти. Странные, нелогичные ассоциации

способствуют лучшему запоминанию.

Для эффективного запоминания правила необходимо привести созданную ассоциацию в движение. «Движение» помогает живо представить образ. Оно делает процесс запоминания не только простым, но и интересным. Ассоциации должны быть необычными, нестандартными, невероятными, смешными и нелепыми. Чем банальнее и скучнее будут ассоциации, тем они менее эффективны. И наоборот, чем абсурднее связь между элементами, тем она прочнее. Положительные и приятные образы запоминаются быстрее (они близки, доступны и понятны детям) и процесс

запоминания приносит удовольствие.

При создании образов желательно использовать различные цвета.

Создание ассоциаций всегда индивидуально. Хорошо зарекомендовала себя система образов «Эйдос».

«Эйдос» в переводе с греческого языка – яркий образ. Отсюда и название одного из направлений психообразной культуры – эйдетизм. Эйдетизм – это разновидность образной памяти, связанной с таким феноменом человеческого мозга, как умение видеть предмет, который исчез

из поля восприятия.

Эйдетизм присущ детям. Все методы обучения очень похожи на увлекательную игру. Есть дети, которые испытывают затруднения при изучении математики: абстрактные цифры, формулы и многое другое их часто пугают. Применяя образы, учащиеся с удовольствием занимаются математикой.
В учебниках математики правила для заучивания длинные. Для тех учащихся, чья память плохо развита, эти правила заучить наизусть трудно. Система образов помогает понимать, с легкостью воспроизводить научную информацию. Учащиеся качественно усваивают знания, у них лучше развиваются творческие способности, процесс запоминания материала становится более эффективным, т.к. задействовано не только левое полушарие головного мозга, отвечающее за логическое мышление, но и

правое, способствующее развитию образного мышления.

Физиологи пришли к заключению, что при односторонней загрузке левого полушария головного мозга, ведающего речевыми функциями и абстрактным мышлением, уменьшается продуктивность умственного труда. Когда учение упирается только на логическое мышление, возможности мозга используются частично. Перенапряжение левой половины мозга оказывает тормозящее воздействие на его работу в целом. Активизация работы правого полушария представляет резерв повышения эффективности. Физиологи подчеркивают, что необходимо сочетать логическое мышление с образным.
Нововведением системы являются правила-образы в рисунках, которые

назвали « запоминалками».

Тема 1: Сложение и вычитание десятичных дробей (5 класс).

Правило для заучивания в учебнике сформулировано следующим образом:

Чтобы сложить (вычесть) десятичные дроби, нужно:
1) уравнять в этих дробях количество знаков после запятой;
2) записать их друг под другом так, чтобы запятая была записана под запятой;
3) выполнить сложение (вычитание), не обращая внимания на запятую;
4) поставить в ответе запятую под запятой в данных дробях.

Образ: запятая – это капля, которая стекает с лейки

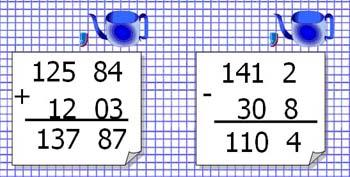
Тема 2: Округление чисел (5 класс).

Если первая отброшенная или замененная нулем цифра равна 5, 6, 7, 8 или 9, то стоящую перед ней цифру увеличивают на 1.
Если первая отброшенная или замененная нулем цифра равна 0, 1, 2, 3 или 4, то стоящую перед ней цифру оставляют без изменения.

Образ: цифры 0, 1, 2, 3, 4 называем «маленькими», а 5, 6, 7, 8, 9 – «большими». Отделяем забором разряд, до которого число необходимо округлить. Через забор могут перебраться только «большие» цифры, при этом цифра, стоящая перед забором, увеличивается на единицу

Тема 3: Умножение десятичных дробей (5 класс).

Чтобы перемножить две десятичные дроби, надо:
1) выполнить умножение, не обращая внимания на запятые;
2) отделить запятой столько цифр справа, сколько их стоит после запятой в обоих множителях вместе.

Образ: в примерах на умножение десятичных дробей цифры, которые стоят после запятой, выделяем другим цветом, т.к. необходимо сосчитать их количество.

Тема 4: Деление десятичных дробей (5 класс).

Чтобы разделить число на десятичную дробь, надо:
1) в делимом и делителе перенести запятую вправо на столько цифр, сколько их после запятой в делителе;
2) после этого выполнить деление на натуральное число.

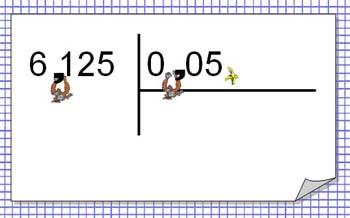
Образ: запятые – это две обезьяны. У второй обезьяны (в делителе) есть цель – достать банан, который лежит за последней цифрой. Она пытается достать банан, в свою очередь первая обезьяна (в делимом) повторяет действия второй обезьяны, т.е. перепрыгивает через столько цифр, через сколько перепрыгнула вторая.

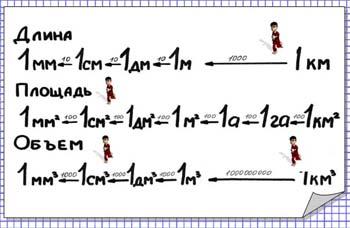
Тема 5: Единицы измерения длины, площади, объема (5 класс).

Образ: при переводе одних единиц измерения (длины, площади, объема) в другие рисуем стрелки, по которым передвигается человечек. Двигаясь по стрелке, он собирает нули, а двигаясь против стрелки – отдает нули.

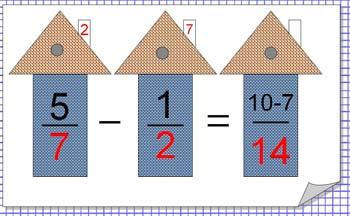
Тема 6: Сложение и вычитание дробей с разными знаменателями (6 класс).

Чтобы привести дроби к общему знаменателю, надо:
1) найти наименьшее общее кратное знаменателей этих дробей, оно и будет их наименьшим общим знаменателем;
2) разделить наименьший общий знаменатель на знаменатели данных дробей, т.е. найти для каждой дроби дополнительный множитель;
3) умножить числитель и знаменатель каждой дроби на ее дополнительный множитель.

Образ: рисуем домики, обращаем внимание на дополнительные множители, которые сидят на крыше.

Тема 7: Пропорции (6 класс).

Образ:

Тема 8: Модуль числа (6 класс).

Модуль числа не может быть отрицательным. Для положительного числа и нуля он равен самому числу, а для отрицательного - противоположному числу.

Образ: модуль – это баня, а знак « минус» - грязь. Оказываясь под знаком модуля, отрицательное число «моется» и выходит без знака «минус» - чистым. В бане могут «мыться» (т.е. стоять под знаком модуля) как положительные, так и отрицательные числа.

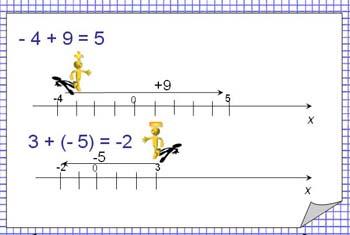
Тема 9: Сложение чисел с помощью координатной прямой (6 класс).

Образ: особую роль играют «человечки» («положительный» и «отрицательный»), позволяющие наглядно моделировать «Математическое сложение положительных и отрицательных чисел » в 6 классе.

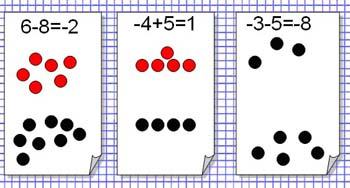
Тема 10: Сложение и вычитание чисел с разными знаками (6 класс).

Чтобы сложить два числа с разными знаками, надо:
1) из большего модуля слагаемых вычесть меньший;
2) поставить перед полученным числом знак того слагаемого, модуль которого больше.

Чтобы сложить два отрицательных числа, надо:
1) сложить их модули;
2) поставить перед полученным числом знак «-».

Образ: черные шашки – это отрицательные числа, белые шашки – положительные. Правила игры: шашка одного цвета «съедает» шашку другого цвета. Выигрывает тот, шашек какого цвета осталось больше.

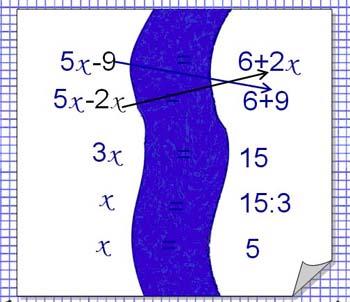
Тема 11: Решение уравнений (6 класс).

Корни уравнения не изменяются, если какое-нибудь слагаемое перенести из одной части уравнения в другую, изменив при этом его знак.

Образ: знак «=» – это река, а знак слагаемого «+» или «-» это одежда. Слагаемое переплывает реку и меняет сырую (например, плюсовую) одежду на сухую (минусовую).

Тема 12: Подобные слагаемые (6 класс).

Чтобы сложить (или говорят: привести) подобные слагаемые, надо сложить их коэффициенты и результат умножить на общую буквенную часть.

Образ: рисуем лица. Девочек «складываем» с девочками, мальчиков - с мальчиками.

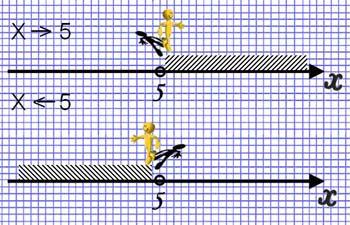
Тема 13: Неравенства (8 класс).

Образ: Когда начинаем изучать неравенства, то у учащихся появляется сложность заштриховать необходимую часть луча. Чтобы ребятам было понятнее, какую часть луча штриховать, дорисовываем знак неравенства до стрелки. Стрелка указывает направление штриховки.

Тема 14: Соотношения между сторонами и углами прямоугольного треугольника (8 класс).

Синусом острого угла в прямоугольном треугольнике называется отношение противолежащего катета к гипотенузе.
Косинусом острого угла в прямоугольном треугольнике называется отношение прилежащего катета к гипотенузе.

Образ: у синуса буква «и» меняется на букву «о», косинуса, буква «о» меняется на букву «и».

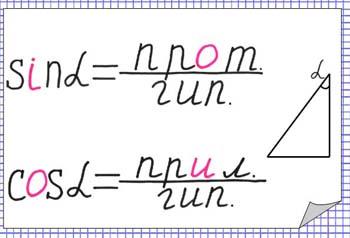
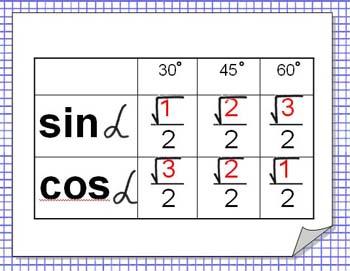
Тема 15: Значения основных углов тригонометрических функций (8 класс).

Образ: для запоминания значения синуса и косинуса для углов 30, 45 и 60 градусов запоминаем числа: для синуса 1, 2, 3, а для косинуса - 3, 2, 1, везде в знаменателе 2, а в числителе знак корня, но т.к. = 1, то у 1 – знак корня не пишем.

Тема 16: Функция. Область определения и область значения функции. Свойства функций (9 класс).

Функцией называют такую зависимость переменной У от Х., при которой каждому значению переменной Х. соответствует единственное значение переменной У.
Все значения независимой переменной образуют область определения.
Все значения, которые принимает независимая переменная, образуют область значений функции. Образ: Х - родители, У - дети; дети зависят от родителей; все родители образуют область значения, дети – область определения.

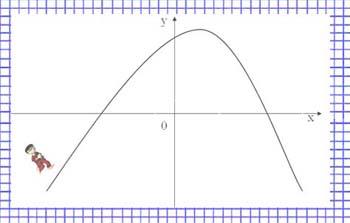
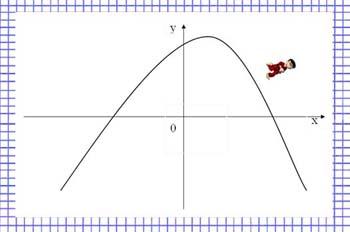
Функция называется возрастающей в некотором промежутке, если большему значению аргумента из этого промежутка соответствует большее значение функции; функция называется убывающей в некотором промежутке, если большему значению аргумента из этого промежутка соответствует меньшее значение функции.

Образ: функция возрастающая – поднимаемся в гору, функция убывающая – спускаемся с горы.

Тема 17: Определение арифметической и геометрической прогрессии (9 класс).

Арифметической прогрессией называется последовательность, каждый член которой, начиная со второго, равен предыдущему члену, сложенному с одним и тем же числом.

Геометрической прогрессией называется последовательность отличных от нуля чисел, каждый член которой, начиная со второго, равен предыдущему члену, умноженному на одно и то же число.

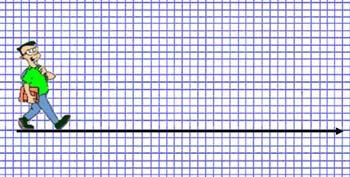
Образ: разность арифметической прогрессии – шаг, длина шага постоянна; знаменатель геометрической прогрессии – прыжок, длина прыжка увеличивается или уменьшается.

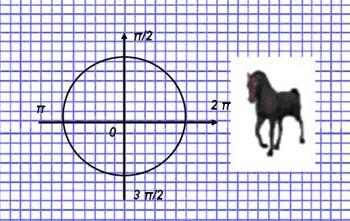
Тема 18: Формулы приведения (9 класс).

Функция в правой части равенства берется с тем же знаком, какой имеет исходная функция, если считать, что угол п является углом I четверти.

Для углов п±п и 2±п название исходной функции сохраняется; для углов п/2±п и 3/2п±п название исходной функции заменяется (синус на косинус, косинус на синус, тангенс на котангенс, котангенс на тангенс).

Образ: формулы приведения – правило лошади. Смотря на единичную окружность, а именно на п/2 и 3п/2 (расположены на оси ординат) – киваем головой сверху вниз, когда же смотрим на п и 2п (расположены на оси абсцисс) – мотаем головой слева на право.