Просмотр содержимого документа
«Объем цилиндра, конуса, усеченного конуса, шара, частей шара.»
Математика
Группа СД 23
Занятие №17
Дата: 18.03.2020
Тема: Объем цилиндра, конуса, усеченного конуса, шара, частей шара.
Задание:
Рассмотрите теоретические сведения, запишите
- формулу объёма цилиндра,
- формулу объёма конуса,
- формулу объёма шара,
- формулы объёма шарового сегмента и шарового сектора,
Рассмотрите примеры решения задач
Оформите и решите задачи для самостоятельной работы
Направьте работу преподавателю
Критерии оценивания:
Оценка выставляется по критериям
Решена 1 задача - оценка «3»
Решено 2 задачи - оценка «4»
Решено 3 задачи - оценка «5»
ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
Объём цилиндра равен произведению площади основания на высоту.
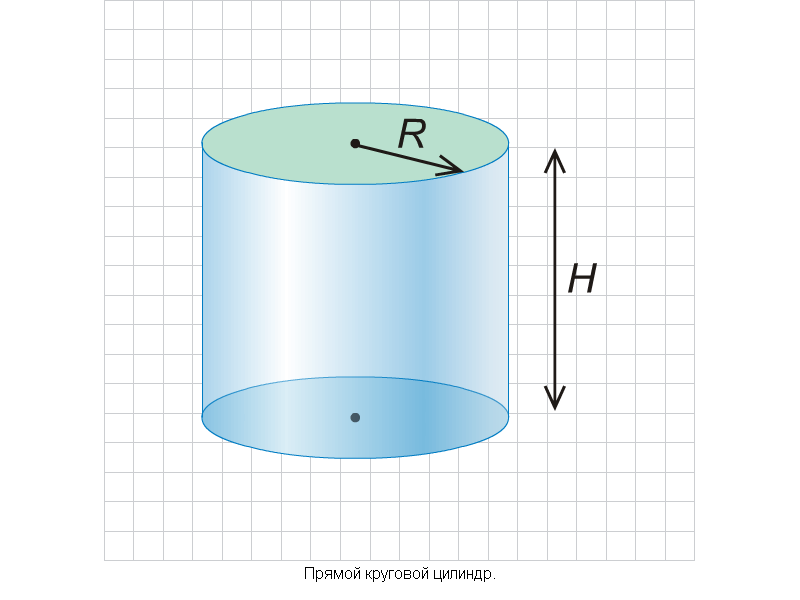
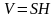
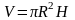
Объем конуса равен одной трети произведения площади основания на высоту.
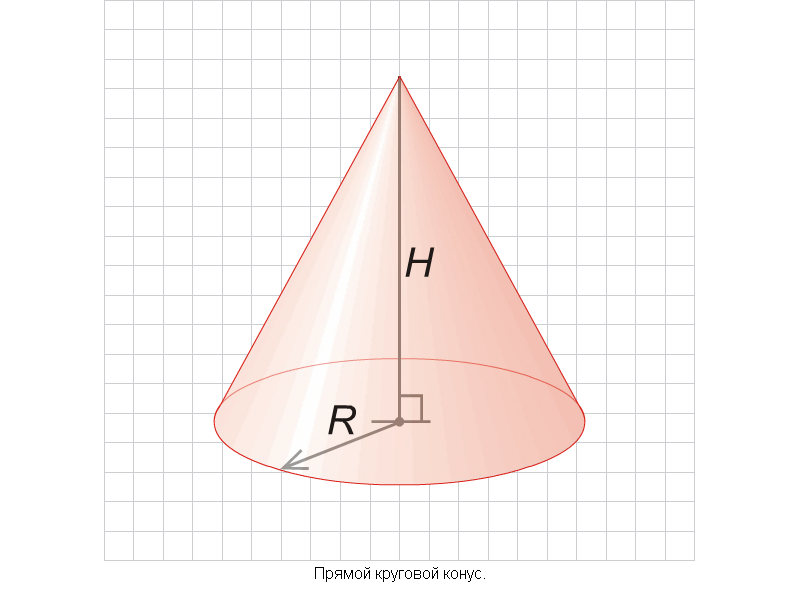
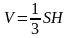
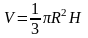
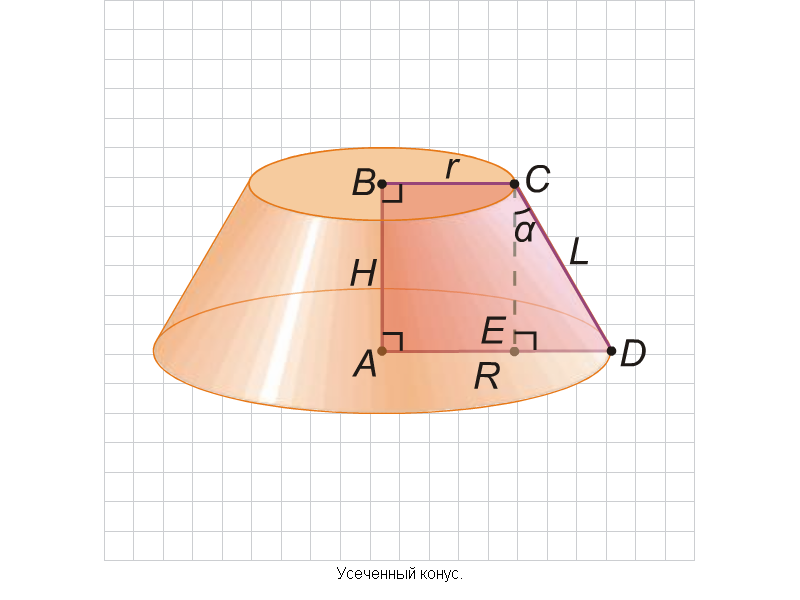
Объем усеченного конуса
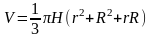
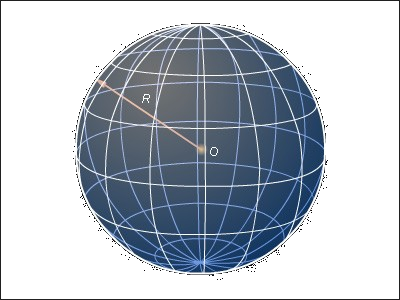
Объем шара радиуса R равен:
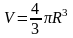
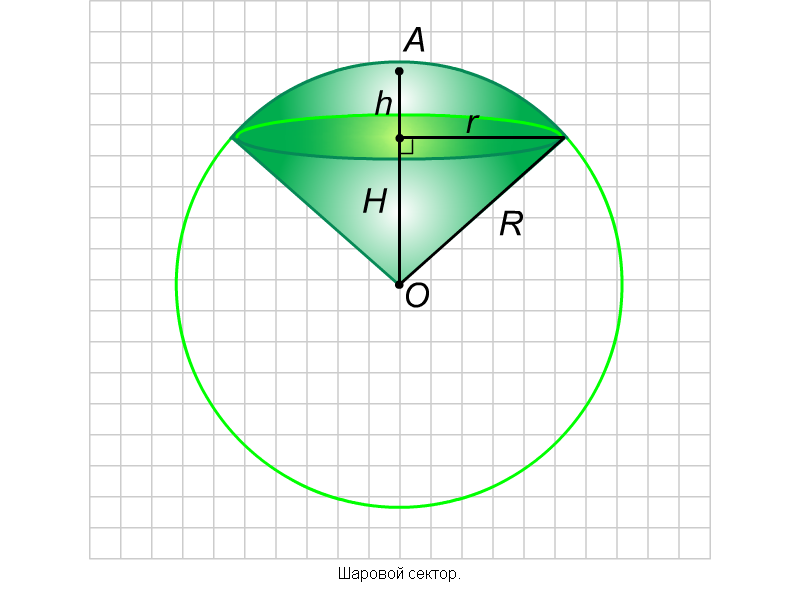
Объем шарового сектора.
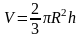
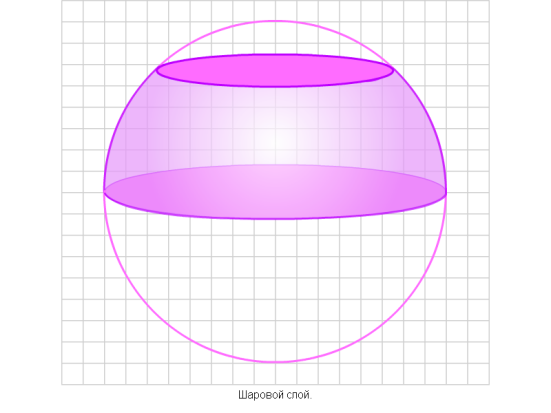
Объем шарового сегмента.
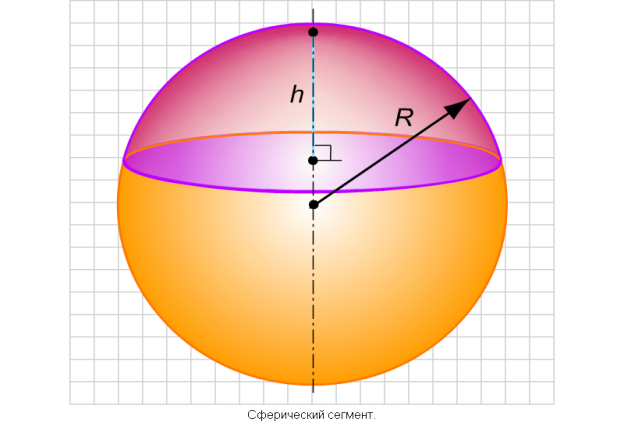
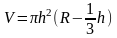
Объем шарового слоя можно вычислить как разность объемов двух шаровых сегментов.
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача 1. Найдите объем цилиндра, если радиус основания равен 2 см, а высота 5 см.
| Дано: Цилиндр R = 2 см h=5 см | Р ешение: ешение:
V = *22*5 = 20 (см3) |
| Найти: V=? | Ответ: V = 20 см3 |
Задача 2. Найдите объем конуса, если его высота 3 см, а радиус основания 4см.
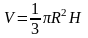
| Дано: Конус R = 4 см h=3 см | Решение:
V =  **42*3 = 16 (см3) **42*3 = 16 (см3) |
| Найти: V=? | Ответ:3 V = 16 см3 |
З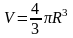 адача 3. Найти объем шара, если его радиус 3см.
адача 3. Найти объем шара, если его радиус 3см.
| Дано: Шар R = 3 см
| Решение:
V = 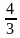 **33 = 36 (см3) **33 = 36 (см3) |
| Найти: V=? | Ответ:3 V = 36 см3 |
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
Задача 1. Найдите объём прямого кругового цилиндра, высота которого 5 дм, а радиус основания 3дм.
Задача 2. Радиус основания конуса равен 48 см, высота его 189 см. Найдите объём конуса.
Задача 3. Радиус шара равен 3,5 дм. Найдите площадь поверхности и объём шара.






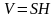
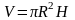

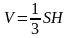
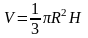

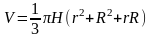

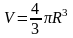

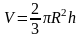

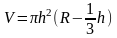

 **42*3 = 16 (см3)
**42*3 = 16 (см3)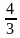 **33 = 36 (см3)
**33 = 36 (см3)









