муниципальное казенное образовательное учреждение
«Черницынская средняя общеобразовательная школа»
Октябрьского района Курской области
ИТОГОВЫЙ ПРОЕКТ
на тему
«Объёмное геометрическое моделирование.
Создание геометрических тел с применением 3D-технологий»
по дисциплине
«Информатика»
Обучающийся: Цуканов Дмитрий
Класс 11А
Руководитель проекта: Пятницков С.В. 26 марта 2024 г.
с.Черницыно
С | 3 |
|
6 |
| 6 |
| 9 |
| 11 |
| 12 |
| 12 |
| 20 |
| 24 |
| 25 |
одержание
ВВЕДЕНИЕ ………………………………………………………………………………..
ГЛАВА I. Теоретический обзор материала по теме исследования
1.1. Геометрические тела ……………………………………………………………….…
1.2. Программы для 3d моделирования (название, краткое описание) ………………...
1.3. История создания программы «Компас-3D» ………………………………………..
ГЛАВА II. Описание исследования и его результаты
2.1. Правила работы в программе «Компас-3D» …………………………………….…..
2.2. Конструирование моделей объёмных геометрических фигур …………………..…
2.3. Технологическая карта на изготовление моделей геометрических фигур с использованием программы «Компас-3D». Экономическое обоснование ……………
ЗАКЛЮЧЕНИЕ……………………………………………...............................................
СПИСОК ИНФОРМАЦИОННЫХ ИСТОЧНИКОВ ………………………………..
ПРИЛОЖЕНИЕ
ВВЕДЕНИЕ
3D ‒ это не только модная аббревиатура из сферы IT, но это ещё дефицитная и, как следствие, высокооплачиваемая технология. 3D-моделирование сравнительно новое направление для обучения компьютерных специалистов с творческими наклонностями.
Не все до конца знают, в чём заключается его суть. Представление большинства кратко и ограничивается тем, что это создание трёхмерных объёмных фигур. Однако области применения 3D-моделирования обширны.
Можно выделить 3 крупные отрасли, которые сегодня невозможно представить без применения трехмерных моделей. Это: индустрия развлечений; медицина; промышленность.
С первой мы сталкиваемся почти каждый день. Это фильмы, анимация и 90% компьютерных игр. Все виртуальные миры и персонажи созданы с помощью одного и того же принципа — полигонального моделирования (Рис. 1).
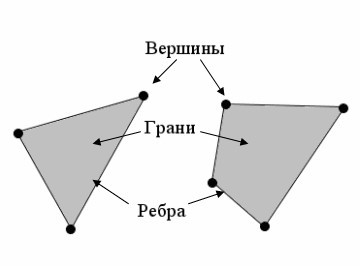

Рис.1. Полигональное моделирование Рис.2. Полигоны
Полигонами (Рис. 2) называются вот эти треугольники и четырехугольники.
Чем больше полигонов на площадь модели, тем точнее модель. При полигональном моделировании мы получаем визуальный образ. Если полигональная модель выполнена в виде замкнутого объема, например, скульптуры, то благодаря современной технологии 3D-печати они могут быть воплощены в жизнь.
 Полигональное моделирование нужно не только для творческих людей (художников, дизайнеров, скульпторов). Еще одной крупной сферой применения 3D моделей является медицина, а именно – хирургия. Можно вырастить протез кости взамен раздробленной. Конечно, используя полигональное моделирование, можно построить все восстанавливающие и усиливающие элементы, но невозможно контролировать необходимые зазоры, сечения, учесть физические свойства материала и технологию изготовления (особенно плечевого сустава). Для таких изделий применяются методы
Полигональное моделирование нужно не только для творческих людей (художников, дизайнеров, скульпторов). Еще одной крупной сферой применения 3D моделей является медицина, а именно – хирургия. Можно вырастить протез кости взамен раздробленной. Конечно, используя полигональное моделирование, можно построить все восстанавливающие и усиливающие элементы, но невозможно контролировать необходимые зазоры, сечения, учесть физические свойства материала и технологию изготовления (особенно плечевого сустава). Для таких изделий применяются методы
Рис.3. промышленного проектирования.
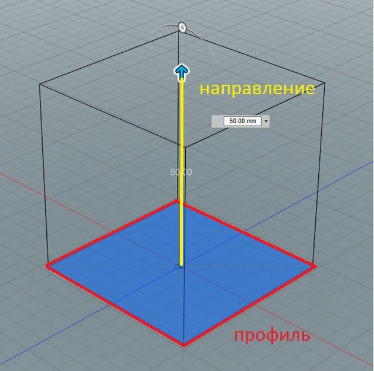
По правильному они называются: САПР (Система Автоматизированного ПРоектирования) или по-английски CAD (Computer-Aided Design). Это принципиально другой тип моделирования. И именно о нем я буду рассказывать. Этот метод отличается от полигонального, тем, что тут нет никаких полигонов и все формы являются цельными и строятся по принципу профиль + направление (Рис. 3).
Базовым типом является твердотельное моделирование. Из названия можно понять, что, если мы разрежем тело, внутри оно не будет пустым. Твердотельное моделирование есть в любой CAD-системе. В CAD мы получаем электронно-геометрическую модель изделия. Твердотельное моделирование отлично подходит для проектирования всего, что получается путем промышленного производства.
Не всегда задуманную топологию и сложность формы можно реализовать в твердотелке, и тогда на помощь приходит неотъемлемая часть промышленного проектирования — поверхностное моделирование.
Актуальность выбранной темы обусловлена практически повсеместным использованием трехмерного моделирования в различных отраслях и сферах деятельности, знание которого становится все более необходимым для полноценного развития личности.
Объектом исследования являются геометрические тела.
Предмет исследования: методы построения моделей геометрических фигур с помощью программы «Компас-3D».
Цель исследования: создать методом 3D-печати наглядное пособие по стереометрии - набор геометрических тел.
Задачи исследования:
Познакомиться с объёмными геометрическими телами
Изучить программы для 3D-моделирования
Сконструировать трехмерные модели геометрических фигур с использованием программы «Компас-3D»
Распечатать модели геометрических фигур на 3D- принтере
Провести экономическое обоснование на изготовление моделей геометрических фигур с использованием программы «Компас-3D»
Решение поставленных задач потребовало привлечения следующих методов исследования:
Работа с различными источниками информации по теме исследования
Описание, систематизация материала, анализ, сравнение
Конструирование
Формы фиксирования результатов:
Скриншоты этапов работы
Описание последовательности выполнения моделей
Готовые модели геометрических тел.
Оснащение и оборудование: программа «Компас-3D» и принтер ZENIT 3D.
Гипотеза: изучение 3D-моделирования способствует развитию пространственного мышления и аккуратности.
Теоретическая и практическая значимость данной работы определяется тем, что мое наглядное пособие по стереометрии – отличный «помощник» на уроках геометрии, как в электронном виде, так и в напечатанном виде на 3D-принтере. Ведь возможность увидеть развертку фигуры, вращать ее, соединять с другими фигурами, заключать одни фигуры внутрь других или же менять форму объемного тела поможет развивать пространственное мышление.
ГЛАВА I. Теоретический обзор материала по теме исследования
1.1. Геометрические тела
Геометрическое тело — некоторый участок пространства, ограниченный замкнутой поверхностью. Множество поверхностей, ограничивающих геометрическое тело, называют его формой.
Существует огромное число геометрических тел. Все они имеют различную форму: от простой до очень сложной, различный способ образования. Однако есть то, что является общим для всех существующих тел — свойство, присущее всем материальным объектам нашего мира — трехмерность.
Трехмерность любого тела говорит о том, что тело в пространстве имеет три однородных измерения: длину, широту и высоту.
Все геометрические тела можно разделить на два типа: многогранники и тела вращения.
Многогранником называется геометрическое тело, поверхностью которого является конечное число многоугольников, каждая сторона любого многоугольника является стороной двух и только двух граней, не лежащих в одной плоскости. Многоугольники – грани многогранника.
Основными элементами многогранника являются:
Грань — поверхность, ограничивающая многогранник.
Ребро — линия пересечения двух соседних граней.
Вершина — точка, в которой пересекаются два или более ребра.
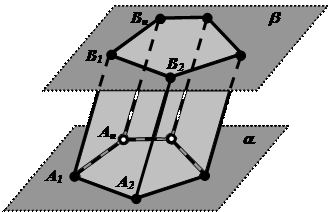
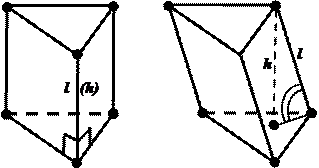
Рис.4. Призма Рис.5. Прямая и наклонная призмы
Многогранник, две грани которого многоугольники, принадлежащие параллельным плоскостям, а остальные грани – параллелограммы, называется призмой (Рис.4). Многоугольники, принадлежащие параллельным плоскостям – основания призмы. Параллелограммы – боковые грани призмы.
Призма называется прямой, если ее боковые ребра перпендикулярны к основаниям, в противном случае призма называется наклонной (Рис.5).
Призма называется треугольной, четырехугольной, пятиугольной и т.д. в зависимости от того, какой многоугольник лежит в ее основании.
Прямая призма называется правильной, если ее основаниями являются правильные многоугольники.
Призма, основанием которой является параллелограмм, называется параллелепипедом (Рис.6).
Прямым параллелепипедом называется параллелепипед, боковые ребра которого перпендикулярны основаниям (Рис.7).
Прямой параллелепипед, основания которого прямоугольники, называется прямоугольным параллелепипедом.
Длины непараллельных ребер прямоугольного параллелепипеда называются линейными размерами (измерениями) прямоугольного параллелепипеда (длина, ширина, высота).

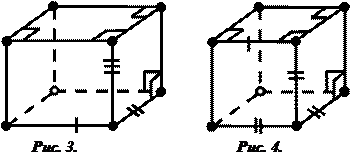
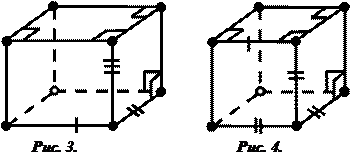 Прямоугольный параллелепипед, все линейные размеры которого равны между собой, называется кубом (Рис. 8).
Прямоугольный параллелепипед, все линейные размеры которого равны между собой, называется кубом (Рис. 8).
| Рис.6. Параллелепипед | Рис.7. Прямой и прямоугольный параллелепипеды | Рис. 8. Куб |
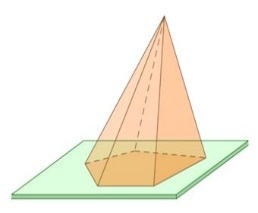
Пирамида — многогранник, основание которого — многоугольник, а остальные грани — треугольники, имеющие общую вершину (Рис.9).
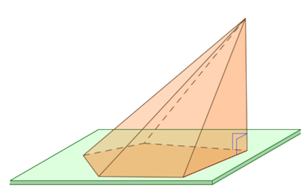
Пирамида называется прямоугольной, если одно из боковых рёбер пирамиды перпендикулярно основанию (Рис.10). Тогда, это ребро и есть высота пирамиды.
Пирамида называется правильной, если её основанием является правильный многоугольник, а вершина проецируется в центр основания (Рис.11).
 У
У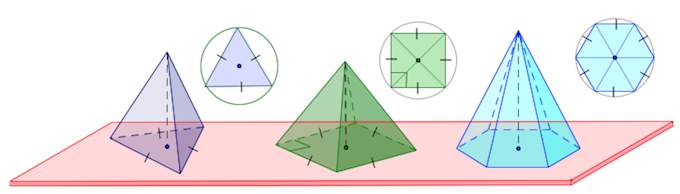
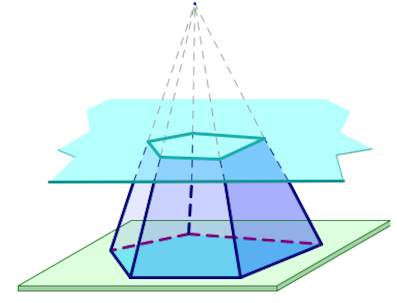
 сечённой пирамидой называется многогранник, заключённый между основанием пирамиды и секущей плоскостью, параллельной её основанию (Рис.12).
сечённой пирамидой называется многогранник, заключённый между основанием пирамиды и секущей плоскостью, параллельной её основанию (Рис.12).
| Рис.9. Пирамида | Рис.10. Прямая пирамида | Рис.11. Правильная пирамида | Рис. 12. Усечённая пирамида |
Тело вращения — тело, полученное в результате вращения плоской фигуры вокруг оси, лежащей в той же плоскости, что и фигура.
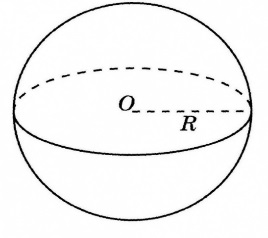


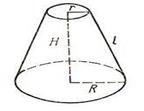
| Рис.13. Шар | Рис.14. Цилиндр | Рис.15. Конус | Рис. 16. Усечённый конус |
Геометрическое тело, полученное при вращении полукруга вокруг его диаметра, называется шаром (Рис.13).
Геометрическое тело, полученное при вращении прямоугольника вокруг одной из его сторон, называется прямым круговым цилиндром (Рис.14). Цилиндр называется прямым, если его образующие перпендикулярны плоскостям оснований.
Геометрическое тело, полученное при вращении прямоугольного треугольника вокруг одного из катетов, называется прямым круговым конусом (Рис. 15).
Геометрическое тело, полученное при вращении прямоугольной трапеции вокруг её боковой стороны, перпендикулярной основаниям, называется прямым круговым усечённым конусом. (Рис.16).
В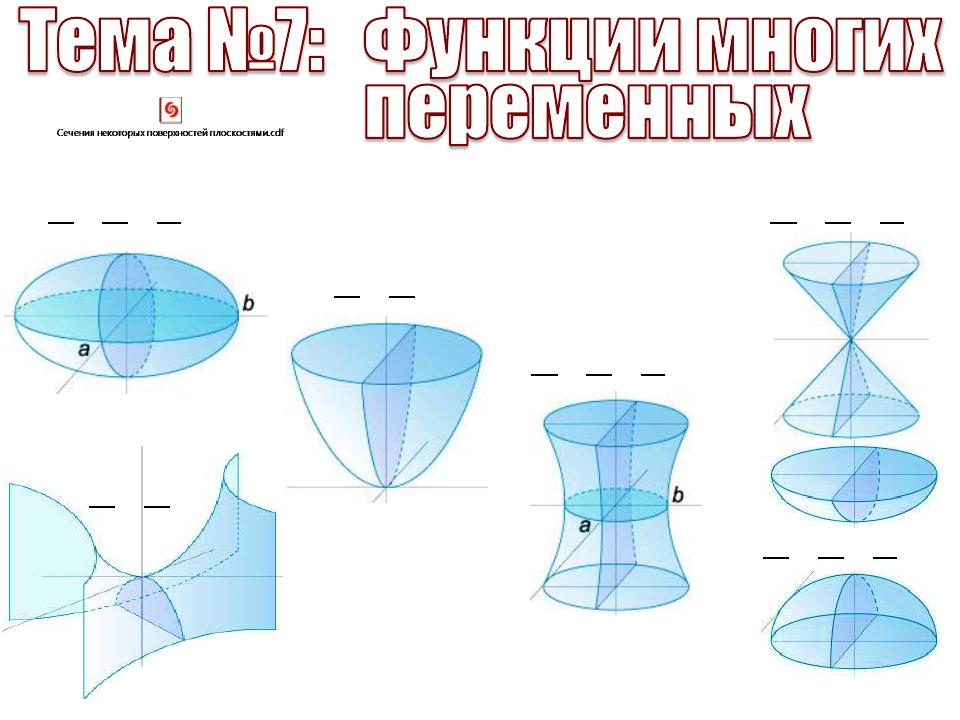

 старших классах я вновь обратился к данной теме. Такие кривые, как эллипс, парабола, гипербола входят в школьное обучение. Они образуют ряд интересных геометрических тел, так же являющимися телами вращения, вот только уже второго порядка (Рис. 17). Это уже не школьная геометрия.
старших классах я вновь обратился к данной теме. Такие кривые, как эллипс, парабола, гипербола входят в школьное обучение. Они образуют ряд интересных геометрических тел, так же являющимися телами вращения, вот только уже второго порядка (Рис. 17). Это уже не школьная геометрия.
Рис.17. Тела вращения второго порядка: эллипсоид, эллиптический параболоид, однополостный гиперболоид
Математическое описание этих тел достаточно сложно и не является целью данного проекта. Для объёмного моделирования важно знать основу построения непосредственно параболы, гиперболы и эллипса. В результате получились красивые и необычные фигуры.
1.2. Программы для 3D-моделирования (название, краткое описание)
WINGS 3D
Программа Wings 3D является продвинутым инструментом для трехмерного моделирования. Пользователям предоставляется множество инструментов, с помощью которых можно создавать очень реалистичные модели. Wings 3D имеет настраиваемый интерфейс, встроенный инструмент отображения AutoUV и может экспортировать готовые файлы в большинство популярных 3D-форматов. Несмотря на все свои достоинства, такие, как поддержка виртуального отображения для симметричного моделирования, Wings 3D не поддерживает анимацию.
DAZ STUDIO
Daz Studio – это мощное и при этом совершенно бесплатное программное обеспечение для трехмерного моделирования. Нельзя сказать, что это легкий для освоения инструмент – новичкам придется долго изучать возможности программы. Создатели программы позаботились о пользовательском опыте, но удобство Daz Studio удастся оценить далеко не сразу. Одной из фишек программы является создание 3D-изображений с GPU ускорением во время рендеринга, что дает возможность создавать очень реалистичные модели. Также в Daz Studio имеется поддержка создания сцен и функционал для анимации моделей.
OPEN SCAD
Программное обеспечение для 3D-моделирования Open SCAD создано для серьезного проектирования (промдизайн, интерьеры, архитектура). Художественные аспекты создателей программы интересовали в гораздо меньшей степени. В отличие от других программ подобного плана, Open SCAD не является интерактивным инструментом – это 3D-компилятор, который отображает детали проекта в трехмерном виде.
AUTODESK 123D
Программа AutoDesk 123D – это большой набор различных инструментов для CAD и 3D-моделирования. С помощью программы можно проектировать, создавать и визуализировать практически любые 3D-модели. AutoDesk также поддерживает технологию 3D-печати. Основной сайт AutoDesk 123D имеет несколько сателлитов, где можно найти множество интересных бесплатных 3D-моделей, с которыми можно поэкспериментировать или просто использовать их в личных целях.
MESHMIXER 3.0
Meshmixer 3.0 позволяет проектировать и визуализировать 3D-конструкции путем объединения двух или нескольких моделей всего за несколько простых шагов. В программе для этого имеется удобная функция «cut and paste», то есть можно вырезать из модели нужные части и вставлять их в другую модель. Программа даже поддерживает лепку – пользователь может создавать виртуальную скульптуру, формируя и уточняя поверхность точно так же, как если бы он лепил модель из глины. И все это в режиме реального времени! Программа поддерживает 3D-печать, готовые модели полностью оптимизированы для отправки в принтер.
3D RESHAPER
3DReshaper является доступным и простым в использовании программным обеспечением для 3D-моделирования. Программу можно использовать в различных областях, таких как искусство, горнодобывающая промышленность, гражданское строительство или судостроение. 3DReshaper поставляется с поддержкой различных сценариев и текстур и имеет множество полезных инструментов и функций, облегчающих процесс трехмерного моделирования.
3D CRAFTER
Бесплатная программа 3D Crafter предназначена для 3D-моделирования в режиме реального времени и создания анимаций. Основная фишка данного редактора – интуитивно понятный подход «drag-and-drop». Сложные модели могут быть построены с помощью простых форм, программа поддерживает скульптурное моделирование и 3D-печать. Это один из самых удобных инструментов для создания анимации.
Blender
Программа Blender является очень мощным и многофункциональным инструментом для работы с трехмерной графикой. Количеством своих функций он практически не уступает большим и дорогим 3ds Max и Cinema 4D. Эта система вполне подойдет как для создания 3D-моделей, так и для разработки видеороликов и мультфильмов. Несмотря на некоторую нестабильность работы и отсутствие поддержки большого числа форматов 3D-моделей, Blender может похвастать перед тем же 3ds Max более продвинутым инструментарием создания анимаций.
Блендер может оказаться сложным в изучении, так как имеет сложный интерфейс, непривычную логику работы и нерусифицированное меню. Зато благодаря открытой лицензии он может быт успешно использован в коммерческих целях.
AUTODESK 3DS MAX
Autodesk 3ds Max — полнофункциональная профессиональная программная система для создания и редактирования трёхмерной графики и анимации, доразработанная компанией Autodesk. Содержит самые современные средства для художников и специалистов в области мультимедиа. Работает в семействе операционных систем Windows
1.3. История создания программы «Компас-3D»
«Ко́мпас» — семейство систем автоматизированного проектирования, универсальная система автоматизированного проектирования, позволяющая в оперативном режиме выпускать чертежи изделий, схемы, спецификации, таблицы, инструкции, расчётно-пояснительные записки, технические условия, текстовые и прочие документы. Изначально система ориентирована на оформления документации в соответствии с Единой системой конструкторской документации (ЕСКД), Единой системой технологической документации (ЕСТД), Системой проектной документации для строительства (СПДС) и международными стандартами, но этим возможности системы не ограничиваются. Разрабатывается российской компанией «Аскон». Название линейки является акронимом от фразы «комплекс автоматизированных систем». Первый выпуск «Компаса» (версия 1.0) состоялся в 1989 году. Первая версия под Windows — «Компас 5.0» — вышла в 1997 году. С 1992 года компания «Аскон» начинает сотрудничать со школами. Образовательная политика АСКОН с 1996 года приобретает завершенные очертания: в вузах активно применяется КОМПАС-График, для преподавания черчения в школах — КОМПАС-Школьник. 2000 год ознаменовался настоящим прорывом: в первой версии КОМПАС-3D позволял создавать трехмерные модели деталей, а затем передавать их в различные системы подготовки программ для станков с ЧПУ и в расчетные пакеты. С 2008 года после участия в национальном проекте «Образование» в каждой школе России начинается установка системы трехмерного моделирования КОМПАС-3D. 2011 год можно отметить выходом первой некоммерческой версии программы «КОМПАС-3D Home». В том же году произошёл выход на международный уровень: открытие европейского представительства АСКОН в Мюнхене, ФРГ. В дальнейшем выпуск новых версий программ позволило компании «Аскон» всё больше завоёвывать рынок информационных технологий. В основе «КОМПАС-3D» лежит российское геометрическое ядро C3D (создано C3D Labs, дочерней компанией АСКОН) и собственные программные технологии, что позволяет заявить о полностью импортонезависимой системе.
ГЛАВА II. Описание исследования и его результаты
2.1. Правила работы в программе «Компас-3D»
Создание объёмных фигур начинается с простого чертежа. В программе 3D-моделирования «Компас-3D» чертёж выполняется в режиме эскиза на плоскости и является типичным примером так называемого 2D-моделирования. Чертежи выполняются с помощью различных элементов линейной геометрии, программа содержит множество простых и сложных элементов и команд. Полученные эскизы являются контурами для формирования объёма. Выполненный чертёж в простом случае может являться основанием всей фигуры, как например квадрат для фигуры куба. В более сложных геометрических фигурах построение производится обычно последовательно и поэтапно. Сначала визуально (или для удобства где-нибудь на бумаге) сложная фигура разбивается на простые геометрические тела, построение которых возможно в рамках одного эскиза и одной операции формирования объёма. Затем последовательно создаются эскизы на плоскостях соприкосновения простых тел, снова формируется объём и т.д. Формирование объёма контуров эскизов и является 3D-моделированием. Основным методом формирования объёма является элемент выдавливания с его опциональными вариациями: линейный элемент выдавливания, элемент вращения и более сложные элементы по траектории и по сечениям. Кроме того, объёмное тело в общем случае можно формировать не только созданием объёма, но и его удалением, т.е. вырезанием. Например, в прямоугольном куске металла необходимо сделать в определённом месте вырез. Можно конечно последовательно создавая прямоугольники и придавая им объём, получить искомый результат. А можно просто создать один прямоугольный объёмный объект, определить положение выреза и одной командой этот вырез произвести. Для этих целей в «Компасе-3D» служит метод вырезания выдавливанием, с теми же опциями что и просто элемент выдавливания, с той лишь разницей указанный объём вырезается (удаляется) из уже имеющегося.
2.2. Конструирование моделей объёмных геометрических фигур
Основой моей работы является не сколько создание объёмных геометрических фигур, а прежде всего всестороннее изучение методов их построения с помощью программы «Компас-3D».
Разберём практическое применение выше описанных методик на примерах конструирования моделей объёмных геометрических фигур.
Куб и цилиндр
В основании квадрат и круг. Единый метод построения объёма – элемент выдавливания. Для наглядности построим вторую локальную систему координат и произведём одновременное построение куба и цилиндра. Построено два эскиза: квадрат со 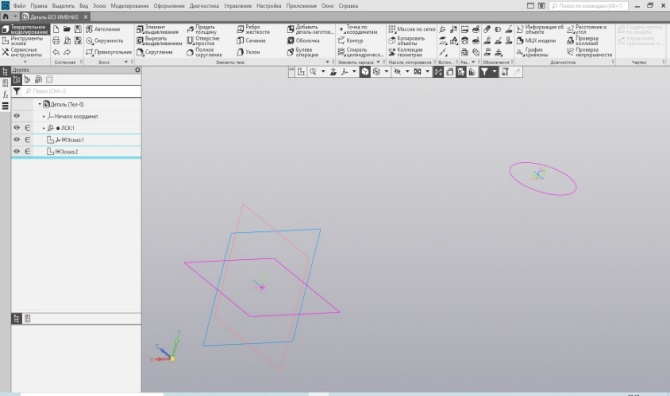
 стороной 50 мм и окружность Ø30 мм (Рис. 18).
стороной 50 мм и окружность Ø30 мм (Рис. 18).
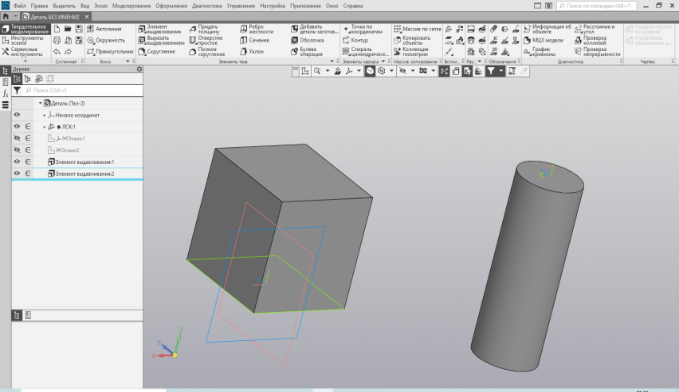
| Рис.18. Эскизы квадрата и окружности | Рис.19. Куб и цилиндр |
Последовательно придадим объём фигурам – куб с выдавливанием на 50мм и цилиндр с выдавливанием на любую произвольную высоту, скажем 80мм.
Шар
Шар – это геометрическое тело, которое является примером тела вращения. Контуром служит половина окружности с центральной осью вращения. Вот и создаём эскиз с построением этого контура. Вариантов построения может быть несколько. Остановлюсь на одном. Строим окружность с диаметром, задающим геометрию будущего шара, скажем 60мм. Строим центральную ось и с помощью метода изменения геометрии «усечь кривую», убираем лишнюю часть окружности (Рис. 20).
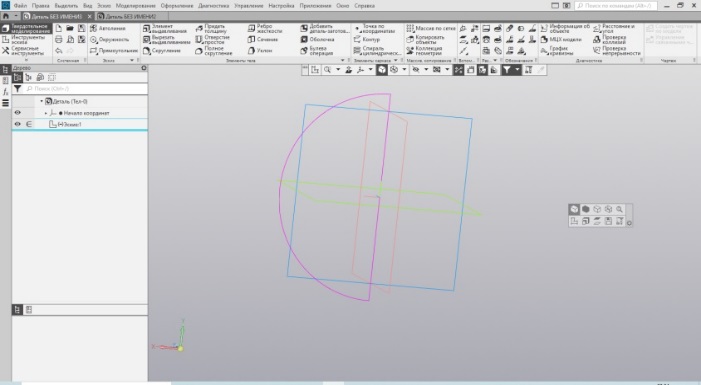
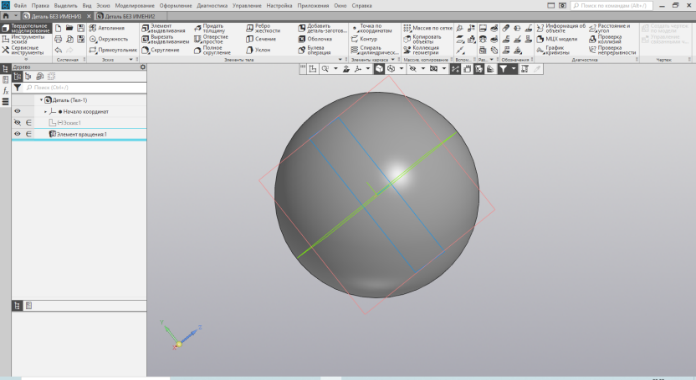 Затем используем частный случай элемента выдавливания – элемент вращения и придаём объём. Отрезок, проведённый через центр окружности, послужил осью вращения. Получаем шар (Рис. 21).
Затем используем частный случай элемента выдавливания – элемент вращения и придаём объём. Отрезок, проведённый через центр окружности, послужил осью вращения. Получаем шар (Рис. 21).
| Рис.20. Эскизы контура окружности | Рис.21. Шар |
Внимательно рассмотрев уже построенную фигуру цилиндра, я понял, что окружность в основании цилиндра даёт возможность считать его тоже фигурой вращения. Сечение цилиндра по вертикальной оси представляет из себя прямоугольник. Итак, вспомним геометрию цилиндра: в основании окружность Ø30 мм и высота фигуры 80 мм.
Легко вычисляем размеры прямоугольного контура вращения: половина от прямоугольника сечения при полной высоте, т.е. 15 мм на 80 мм. Строим эскиз прямоугольника (Рис. 22). И вращаем его. Получается такой же цилиндр (Рис. 23), как и выше.
| 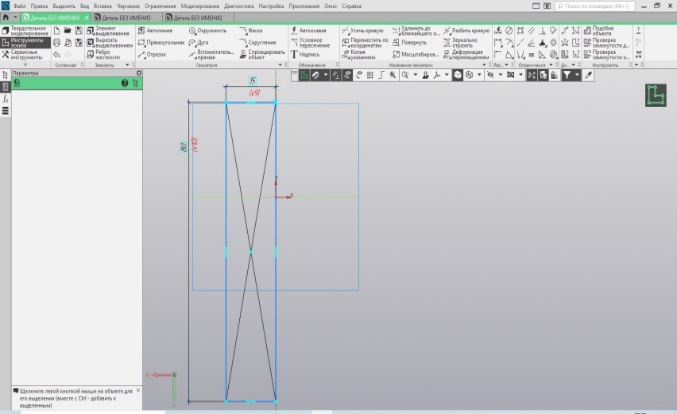 Рис.22. Эскиз прямоугольника Рис.22. Эскиз прямоугольника
| 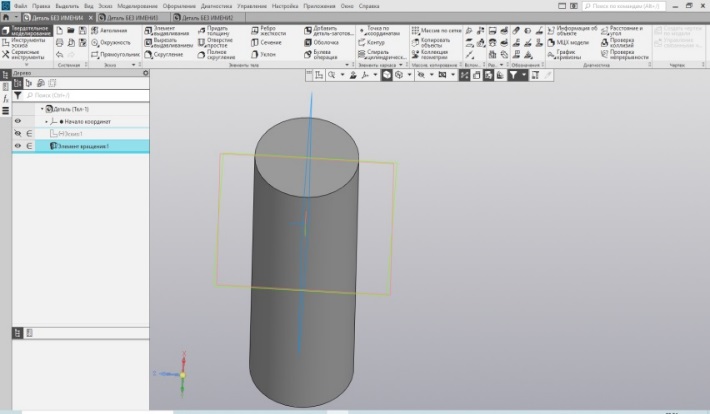 Рис.23. Цилиндр Рис.23. Цилиндр
|
Поставим здесь мысленно закладку, поскольку цилиндр, построенный этим методом, будет использован дальше.
Конус
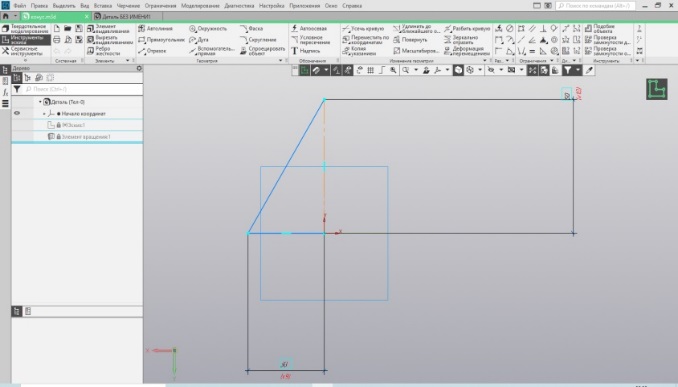
 Следующая фигура вращения – конус. Здесь всё отличие в контуре вращения. В цилиндре – прямоугольник, в конусе прямоугольный треугольник. Построим эскиз прямоугольного треугольника со сторонами: 50 мм – высота конуса, 30 мм – радиус окружности основания (Рис. 24). Используя элемент вращения, получаем объёмную геометрическую фигуру – конус (Рис. 25).
Следующая фигура вращения – конус. Здесь всё отличие в контуре вращения. В цилиндре – прямоугольник, в конусе прямоугольный треугольник. Построим эскиз прямоугольного треугольника со сторонами: 50 мм – высота конуса, 30 мм – радиус окружности основания (Рис. 24). Используя элемент вращения, получаем объёмную геометрическую фигуру – конус (Рис. 25).
| Рис.24. Эскиз прямоугольного треугольника | Рис.25. Конус |
На примере конуса я покажу огромное разнообразие инструментов для 3D-моделирования в программе «Компас-3D».
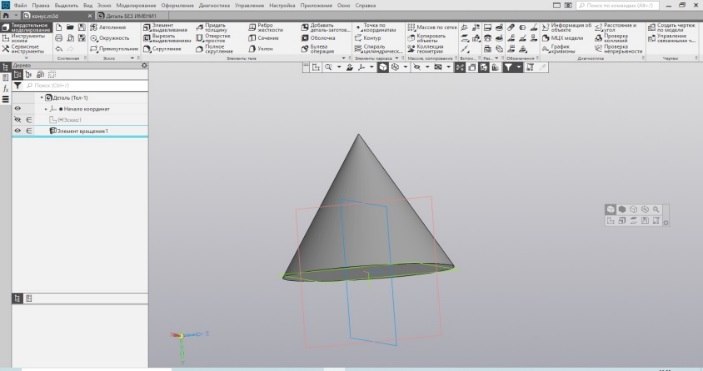
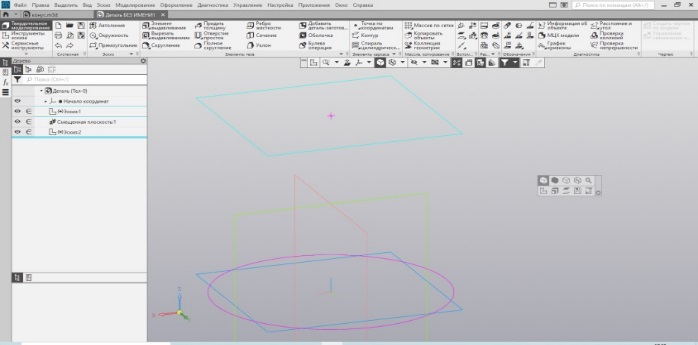
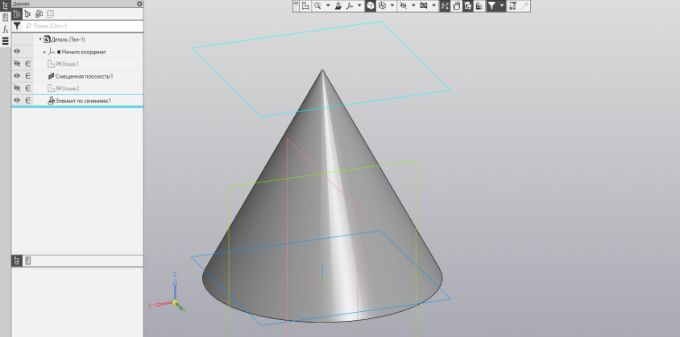
Следующий вариант построения конуса. В основании конуса лежит окружность, вершиной является точка. Построим эти два элемента в двух разных эскизах на смещённых (параллельных) плоскостях, расстояние между которыми равно высоте конуса – 50 мм (Рис.26).
| Рис.26. Эскизы окружности и точки | Рис.27. Конус |
Теперь используем один из вариантов формирования объёма элемента выдавливания – элемент по сечениям. Построенные контуры – окружность и точка – можно рассматривать как контуры сечения, соответственно, соединяя их между собой, получаем тело в пространстве, ограниченное этими сечениями (Рис. 27).
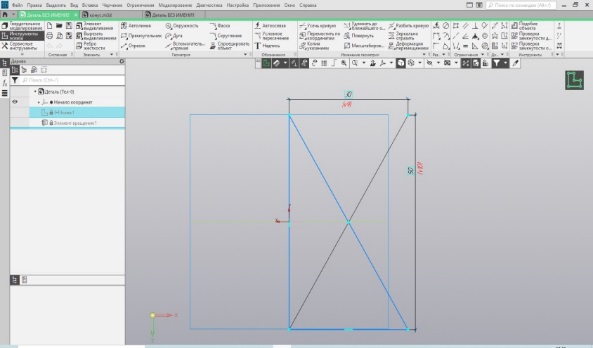 Продолжаем строить конус, ещё один вариант. Вспомним последний вариант построения цилиндра. Отредактируем его и получим снова конус. Открываем в программе цилиндр, построенный вращением прямоугольника, и редактируем эскиз прямоугольника (Рис. 28).
Продолжаем строить конус, ещё один вариант. Вспомним последний вариант построения цилиндра. Отредактируем его и получим снова конус. Открываем в программе цилиндр, построенный вращением прямоугольника, и редактируем эскиз прямоугольника (Рис. 28).
| Рис.28. Редактирование эскиза прямоугольника |
Внесу некоторые пояснения. Стороны прямоугольника выполнены основными линиями, а внутренние диагональные линии – вспомогательными. Удаляем командой «усечь кривую» стороны прямоугольника, образующие внешние стенки цилиндра. У диагональной линии, выполняющей роль гипотенузы прямоугольного треугольника, меняем стиль на «основную». Закрываем редактирование эскиза – опять конус.
Призма
Построим объёмную геометрическую фигуру – призму. Первый, так сказать «ручной» способ построения годен только для простого варианта – треугольной призмы.
Строим из отрезков треугольник и с помощью команды равенства делаем его равносторонним. Далее команда элемента выдавливания на определённую высоту и готова призма. Для призм, в основании которых лежит правильный n-угольник, где n3 следует использовать автоматическое построение многоугольника, которое опционально находится в закладке при построении прямоугольника (Рис. 29). Построим рядом простую и сложную призму. Трёхгранную и пятигранную. Высотой 90 мм и 60 мм (Рис. 30).
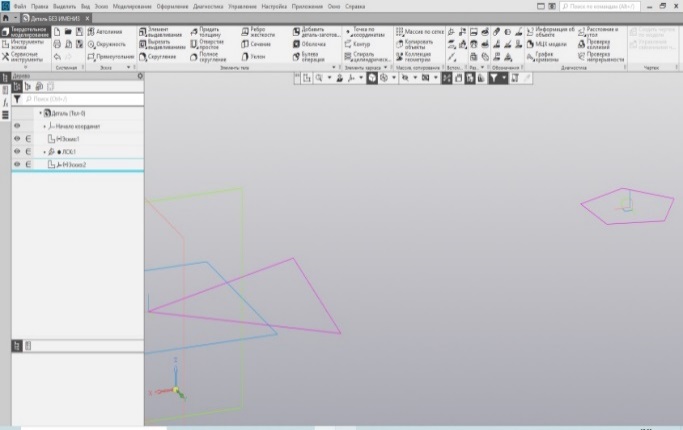
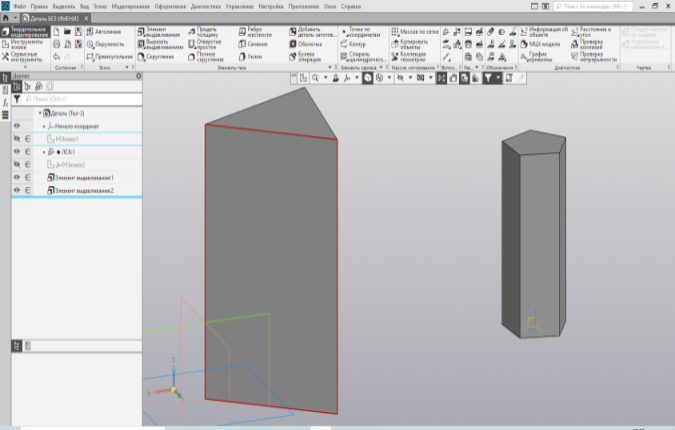
| Рис.29. Эскизы треугольника и пятиугольника | Рис.30. Призмы |
Строить многогранник вручную по всем правилам геометрии довольно затруднительно.
Пирамида
 Построим объёмную геометрическую фигуру – пирамиду. Из вышеописанного можно сделать выводы: построение сложной пирамиды возможно при использовании автоматического построения многогранника, лежащего в её основании.
Построим объёмную геометрическую фигуру – пирамиду. Из вышеописанного можно сделать выводы: построение сложной пирамиды возможно при использовании автоматического построения многогранника, лежащего в её основании.
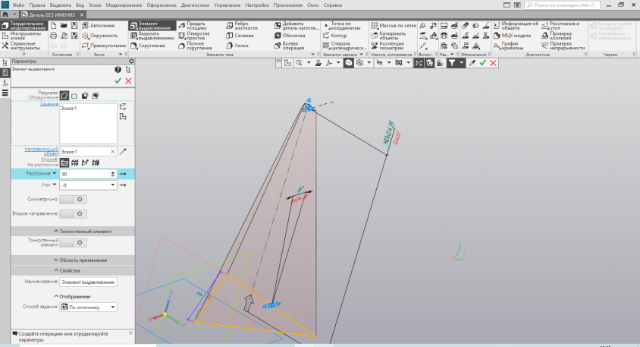
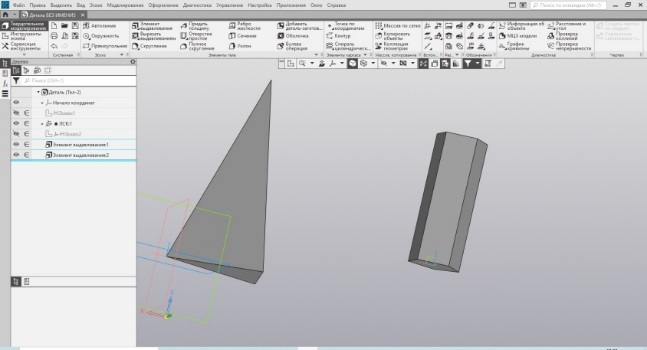
| Рис.31. Преобразование эскиза призмы | Рис.32. Пирамида и призма |
Также можно просто взять готовую призму и преобразовать её в пирамиду. Последним и займёмся, ибо всё остальное является повторением. Для сведения всех точек верхнего основания в одну используем задание угла при построении элемента выдавливания (Рис.31). Подбирая угол в его целой и при необходимости дробной части, добиваемся максимального сведения (для контроля увеличиваем верхнюю точку), при этом стараемся не уйти от заданного размера высоты. Этот метод построения носит относительно приближённый характер и мне не очень нравится. В данном примере угол получился - 9,(1)о. Таким образом построили пирамиду (Рис. 32). Для многогранных пирамид построение аналогично.
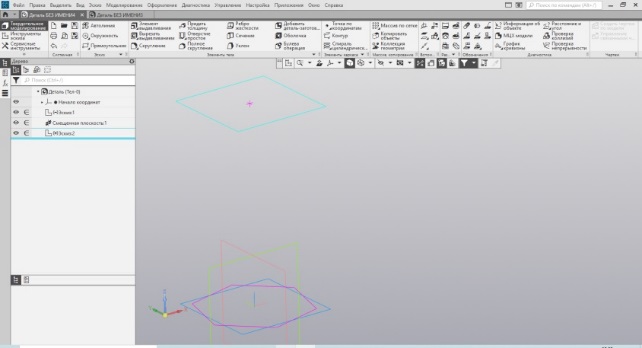
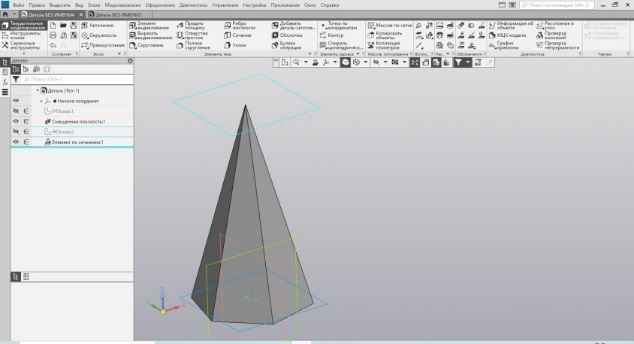 Следующий вариант построения пирамиды основан на уже известном методе использования смещённых плоскостей и формирование объёма элементом по сечениям. В одной плоскости – многоугольник, в другой – точка (Рис. 33). Используем элемент по сечениям и получаем пирамиду (Рис. 34).
Следующий вариант построения пирамиды основан на уже известном методе использования смещённых плоскостей и формирование объёма элементом по сечениям. В одной плоскости – многоугольник, в другой – точка (Рис. 33). Используем элемент по сечениям и получаем пирамиду (Рис. 34).
| Рис.33. Эскизы многоугольника и точки | Рис.34. Пирамида |
Усечённый конус, усечённая пирамида и наклонная призма
Для пополнения коллекции объёмных геометрических фигур, а также изучения новых методов построений получим частные варианты уже построенных фигур: усечённые конус и пирамида и наклонная призма.
У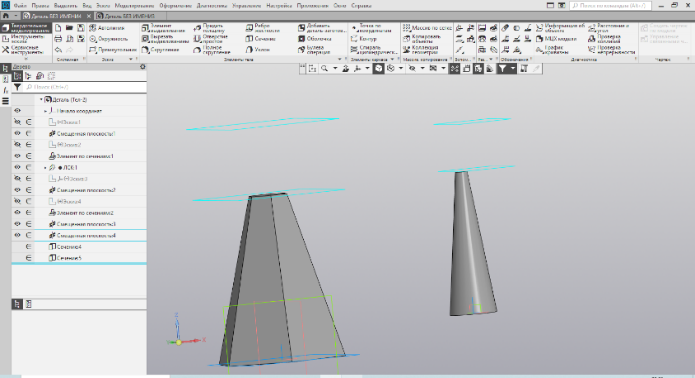
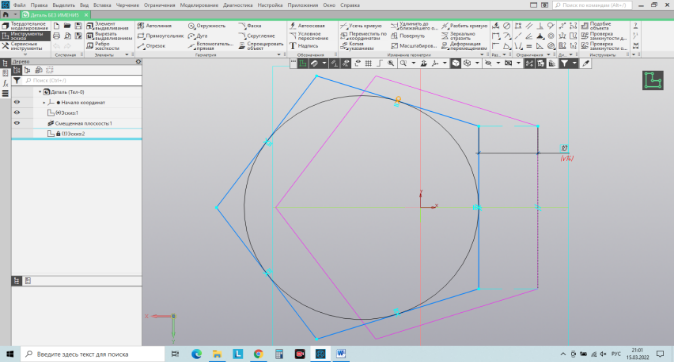 сечение конуса и пирамиды просто и одинаково, по сути. Используется метод смещённых плоскостей. Сам процесс отсечения производится командой «сечение» в разделе «элементы тела». Один нюанс: при усечении рядом стоящих объектов на разных высотах, необходимо в опциях сечения выбирать конкретное тело (Рис. 35).
сечение конуса и пирамиды просто и одинаково, по сути. Используется метод смещённых плоскостей. Сам процесс отсечения производится командой «сечение» в разделе «элементы тела». Один нюанс: при усечении рядом стоящих объектов на разных высотах, необходимо в опциях сечения выбирать конкретное тело (Рис. 35).
| Рис.35. Усечённые пирамида и конус | Рис.36. Построение эскиза наклонной призмы |
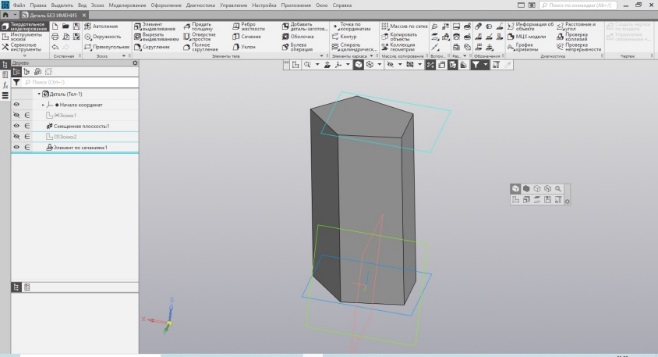
При выполнении наклона призмы придётся поработать со смещением верхнего основания. Здесь я специально оставил открытым один из эскизов, что бы было видно смещение призмы по одной из граней на 10 мм (Рис. 36).
Формирование объёма производится Рис.37. Наклонная призма элементом по сечениям (Рис. 37).
Параболоид, гиперболоид, эллипсоид
Изучение геометрии продолжается. Немного из школьного курса, чисто поверхностно, я узнал, что на основе такие кривых как парабола, гипербола, эллипс, строятся геометрические тела называемые поверхностями вращения второго порядка. Естественно строгое и подробное изучение этих тел выходит за рамки школьного обучения, однако я решил их построить с чисто ознакомительными целями.
Проще всего было с эллипсоидом. Во встроенных библиотеках программы «КОМПАС-3D» есть возможность автоматического построения эллипса, чем можно воспользоваться. Строим эскиз эллипса (Рис. 38), проставляем размеры, из раздела «изменение геометрии» с помощью двух команд – разбить кривую и усечь кривую, сначала разбиваем кривую эллипса на две части и одну из них отсекаем (Рис. 39).
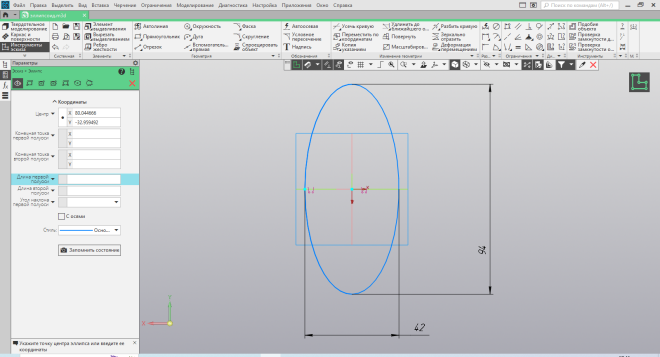
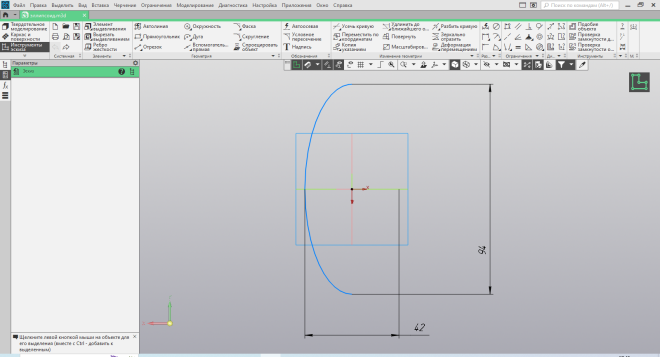
| Рис.38. Эскиз эллипса | Рис.39. Усечение эллипса |
| Рис.40. Придание объёма эллипсоиду | Рис.41. Изменение размеров |
Д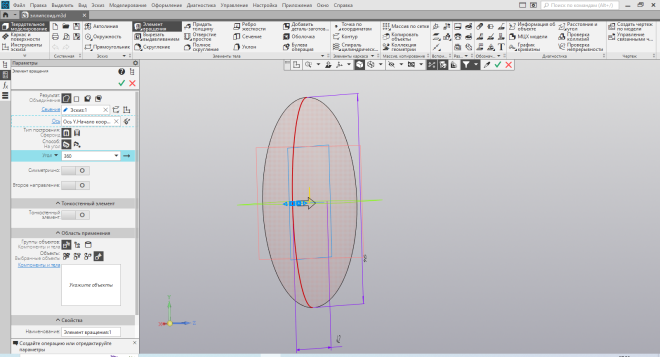
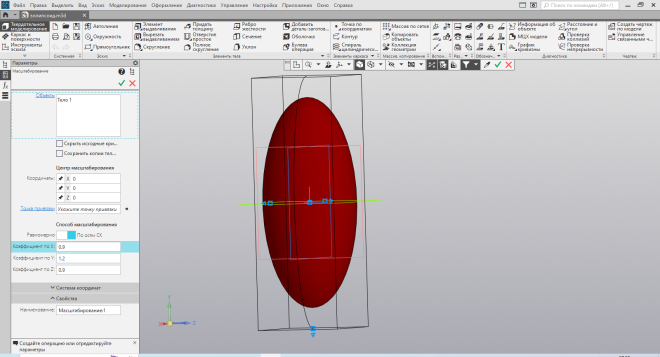 алее с помощью команды формирования объёма – элемента выдавливания, а именно его частного случая, элемента вращения – получаем объёмную фигуру эллипсоида (Рис. 40). В разделе меню «моделирование» есть очень полезная команда масштабировать, которую я использую для изменения размеров (Рис. 41) эллипсоида, причём по каждой оси можно задавать свой коэффициент масштаба.
алее с помощью команды формирования объёма – элемента выдавливания, а именно его частного случая, элемента вращения – получаем объёмную фигуру эллипсоида (Рис. 40). В разделе меню «моделирование» есть очень полезная команда масштабировать, которую я использую для изменения размеров (Рис. 41) эллипсоида, причём по каждой оси можно задавать свой коэффициент масштаба.
Для параболоида и гиперболоида вспомним школьный курс. Формула параболы y=x2 и гиперболы – y=1/x. Они необходимы для задания точек, по которым будут строится кривые.
Параболоид. На эскизе (Рис. 42) по точкам строим одну из ветвей параболы. Далее повторяем. Объём – элементом вращения (Рис. 43), изменяем размеры (Рис. 44) с помощью команды масштабировать, что очень удобно – не надо перестраивать кривую,
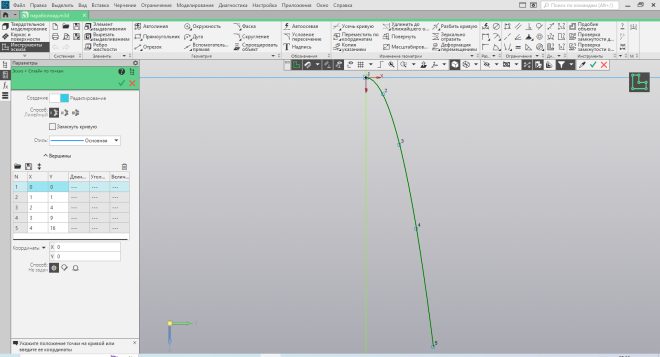
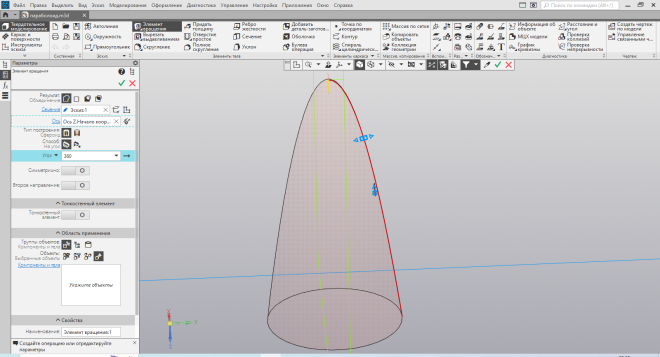
| Рис.42. Эскиз параболы | Рис.43. Придание объёма параболоиду |
в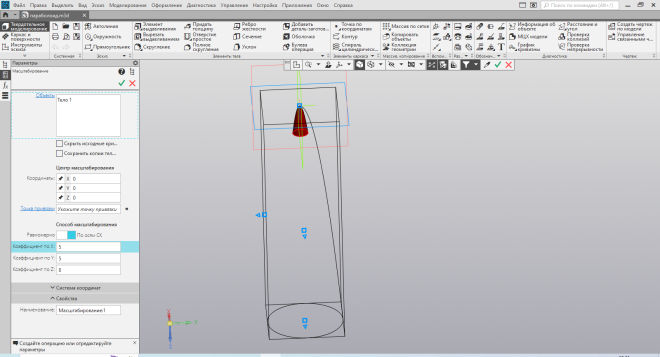 ычислять точки, а просто многократно изменяя коэффициенты масштаба, добиться необходимого внешнего вида.
ычислять точки, а просто многократно изменяя коэффициенты масштаба, добиться необходимого внешнего вида.
| Рис.44. Изменение размеров |
| Рис.45. Эскиз гиперболы | Рис.46. Придание объёма гиперболоиду |
Г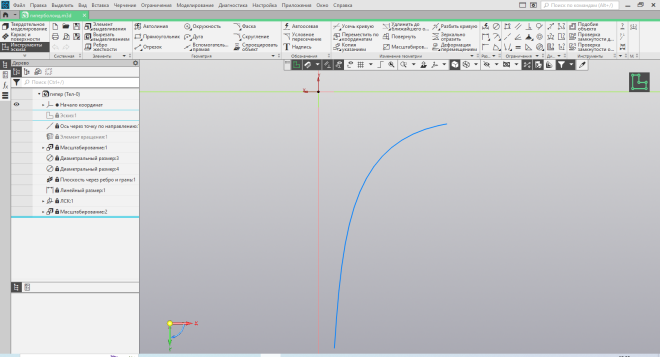
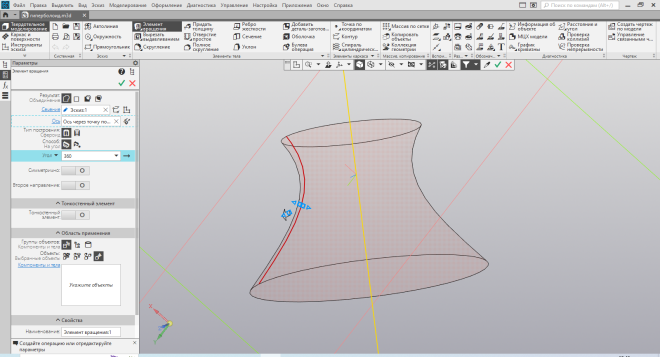
 иперболоид. Построение аналогично предыдущим с некоторым нюансом. На эскизе (Рис. 45) по точкам строим одну из ветвей гиперболы. При использовании элемента вращения, ось вращения строится в процессе создания объёма под вполне логичным углом в 45 или по вектору с координатами точек (0;0) и (0,5;0,5) (Рис. 46).
иперболоид. Построение аналогично предыдущим с некоторым нюансом. На эскизе (Рис. 45) по точкам строим одну из ветвей гиперболы. При использовании элемента вращения, ось вращения строится в процессе создания объёма под вполне логичным углом в 45 или по вектору с координатами точек (0;0) и (0,5;0,5) (Рис. 46).
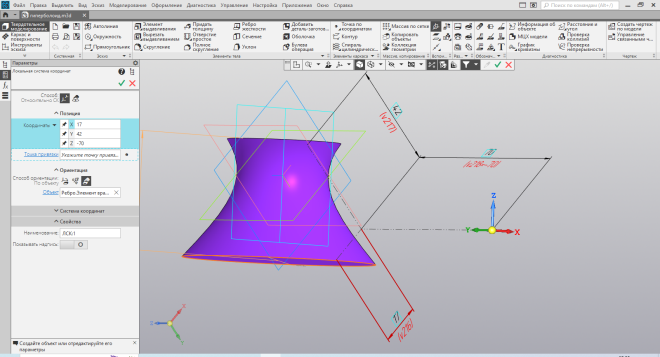
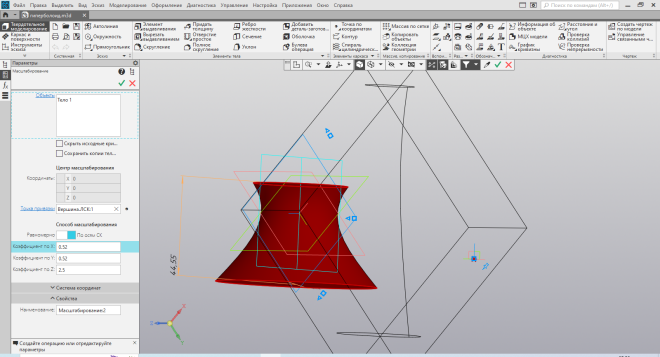
| Рис.47. Построение локальной системы координат | Рис.48. Изменение размеров |
Построив гиперболоид по оси вращения отличной от осей стандартной системы координат, соответственно строю другую локальную систему координат (Рис. 47) и уже с её помощью изменяю размеры (Рис. 48).
2.3. Технологическая карта на изготовление моделей геометрических фигур с использованием программы «Компас-3D». Экономическое обоснование
Таблица 1. Технологическая карта на изготовление моделей геометрических фигур с использованием программы «Компас-3D»
| Фигура / Параметры (на 1 ед.дет.) | Используемый пластик | Толщина оболочки детали | Скорость печати | Процент заполнения | Поддержка | Время печати |
| Куб | PLA | 0,60 мм | 42 мм/сек | 20% | нет | 1ч 48мин |
| Шар | PLA | 0,60 мм | 42 мм/сек | 20% | нет | 1ч 45мин |
| Цилиндр | PLA | 0,60 мм | 42 мм/сек | 20% | нет | 1ч 35мин |
| Конус | PLA | 0,60 мм | 42 мм/сек | 20% | нет | 50мин 44с |
| Пирамида | PLA | 0,60 мм | 42 мм/сек | 20% | нет | 47мин 33с |
| Призма | PLA | 0,60 мм | 42 мм/сек | 20% | нет | 1ч 31мин |
| Усечённый конус | PLA | 0,60 мм | 42 мм/сек | 20% | нет | 38 мин 16с |
| Усечённая пирамида | PLA | 0,60 мм | 42 мм/сек | 20% | нет | 36 мин 04с |
| Наклонная призма | PLA | 0,60 мм | 42 мм/сек | 20% | нет | 1ч 31мин |
| Эллипсоид | PLA | 0,60 мм | 42 мм/сек | 20% | нет | 2ч 43мин |
| Параболоид | PLA | 0,60 мм | 42 мм/сек | 20% | нет | 2ч 40мин 34с |
| Гиперболоид | PLA | 0,60 мм | 42 мм/сек | 20% | нет | 1ч 47мин |
| ИТОГО | 18ч 13мин 11с |
Определим себестоимость изделия (набор моделей геометрических фигур) по формуле: С = П + ОТ +Э, где
С – себестоимость изделия,
П - материальные затраты на пластик для печати моделей геометрических фигур,
ОТ - отчисление на оплату труда,
Э - материальные затраты на стоимость электроэнергии.
Расход пластика на каждую модель можно получить на этапе подготовки модели (слайсинга) к печати.
Таблица 2. Материальные затраты на пластик для печати моделей геометрических фигур с использованием программы «Компас-3D»
| № п/п | Наименование фигуры | Кол-во пластика на 1 фигуру (м) | Кол-во геометрических фигур (шт.) | Стоимость 1 м пластика (руб.) | Стоимость пластика в расчете на 1 фигуру (руб.) |
| 1 | Куб | 9,2 | 1 | 4,2 | 38,64 |
| 2 | Шар | 8,4 | 1 | 4,2 | 35,28 |
| 3 | Цилиндр | 9,2 | 1 | 4,2 | 38,64 |
| 4 | Конус | 3,5 | 1 | 4,2 | 14,7 |
| 5 | Пирамида | 3,1 | 1 | 4,2 | 13,02 |
| 6 | Призма | 7,6 | 1 | 4,2 | 31,92 |
| 7 | Усечённый конус | 2,5 | 1 | 4,2 | 10,5 |
| 8 | Усечённая пирамида | 2,2 | 1 | 4,2 | 9,24 |
| 9 | Наклонная призма | 7,5 | 1 | 4,2 | 31,5 |
| 10 | Эллипсоид | 16,8 | 1 | 4,2 | 70,56 |
| 11 | Параболоид | 16,2 | 1 | 4,2 | 68,04 |
| 12 | Гиперболоид | 10,7 | 1 | 4,2 | 44,94 |
| ИТОГО | 96,9 | - | 4,2 | 406,98 |
Расходы на оплату труда по созданию моделей геометрических фигур:
1кг пластика – 315 м, 1000 : 315 = 3,17 (г) – весит 1 м
Оплата труда по созданию изделия весом 1 г - 50 рублей (по предложениям сайтов фирм, предоставляющих индивидуальные услуги по конструированию и печати 3D изделий).
Таблица 3. Материальные затраты на оплату труда по созданию моделей геометрических фигур с использованием программы «Компас-3D»
| № п/п | Наименование фигуры | Кол-во пластика на 1 фигуру (м) | Вес 1м пластика (г) | Вес 1 фигуры (г) | Стоимость труда по созданию изделия весом 1 г (руб.) | Стоимость труда по созданию изделия (руб.) |
| 1 | Куб | 9,2 | 3,17 | 29,16 | 50 | 1458 |
| 2 | Шар | 8,4 | 3,17 | 26,63 | 50 | 1331,5 |
| 3 | Цилиндр | 9,2 | 3,17 | 29,16 | 50 | 1458 |
| 4 | Конус | 3,5 | 3,17 | 11,1 | 50 | 555 |
| 5 | Пирамида | 3,1 | 3,17 | 9,83 | 50 | 491,5 |
| 6 | Призма | 7,6 | 3,17 | 24,1 | 50 | 1205 |
| 7 | Усечённый конус | 2,5 | 3,17 | 7,93 | 50 | 396,5 |
| 8 | Усечённая пирамида | 2,2 | 3,17 | 6,96 | 50 | 348 |
| 9 | Наклонная призма | 7,5 | 3,17 | 23,77 | 50 | 1188,5 |
| 10 | Эллипсоид | 16,8 | 3,17 | 53,26 | 50 | 2663 |
| 11 | Параболоид | 16,2 | 3,17 | 51,35 | 50 | 2567,5 |
| 12 | Гиперболоид | 10,7 | 3,17 | 33,92 | 50 | 1696 |
| ИТОГО | 96,9 | 3,17 | 307,17 | 50 | 15358,5 |
Стоимость 1 кВт электроэнергии 4,72 руб., потребляемая мощность 3D принтера 300Вт/час, 5 Вт/мин, 0,083 Вт/с
Таблица 4. Материальные затраты на стоимость электроэнергии для печати моделей геометрических фигур с использованием программы «Компас-3D»
| № п/п | Наименование фигуры | Время печати | Кол-во потребленной энергии (кВт) | Стоимость 1 кВт (руб.) | Стоимость электроэнергии для печати 1 фигуры (руб.) |
| 1 | Куб | 1ч 48мин | 0,54 | 4,72 | 2,55 |
| 2 | Шар | 1ч 45мин | 0,525 | 4,72 | 2,48 |
| 3 | Цилиндр | 1ч 35мин | 0,475 | 4,72 | 2,25 |
| 4 | Конус | 50мин 44с | 0,254 | 4,72 | 1,2 |
| 5 | Пирамида | 47мин 33с | 0,238 | 4,72 | 1,12 |
| 6 | Призма | 1ч 31мин | 0,455 | 4,72 | 2,15 |
| 7 | Усечённый конус | 38 мин 16с | 0,191 | 4,72 | 0,9 |
| 8 | Усечённая пирамида | 36 мин 04с | 0,18 | 4,72 | 0,85 |
| 9 | Наклонная призма | 1ч 31мин | 0,455 | 4,72 | 2,15 |
| 10 | Эллипсоид | 2ч 43мин | 0,815 | 4,72 | 3,85 |
| 11 | Параболоид | 2ч 40мин 34с | 0,803 | 4,72 | 3,79 |
| 12 | Гиперболоид | 1ч 47мин | 0,535 | 4,72 | 2,53 |
| Итого | 18ч 13мин 11с | 5,463 | 4,72 | 25,82 |
Таблица 5. Себестоимость изделия для печати моделей геометрических фигур с использованием программы «Компас-3D»
| № п/п | Наименование фигуры | Стоимость пластика в расчете на 1 фигуру (руб.) | Стоимость труда по созданию изделия (руб.) | Стоимость электроэнергии для печати 1 фигуры (руб.) | Себестоимость изделия (руб.) |
| 1 | Куб | 38,64 | 1458 | 2,55 | 1496,64 |
| 2 | Шар | 35,28 | 1331,5 | 2,48 | 1366,78 |
| 3 | Цилиндр | 38,64 | 1458 | 2,25 | 1496,64 |
| 4 | Конус | 14,7 | 555 | 1,2 | 569,7 |
| 5 | Пирамида | 13,02 | 491,5 | 1,12 | 504,52 |
| 6 | Призма | 31,92 | 1205 | 2,15 | 1236,92 |
| 7 | Усечённый конус | 10,5 | 396,5 | 0,9 | 407 |
| 8 | Усечённая пирамида | 9,24 | 348 | 0,85 | 357,24 |
| 9 | Наклонная призма | 31,5 | 1188,5 | 2,15 | 1220 |
| 10 | Эллипсоид | 70,56 | 2663 | 3,85 | 2733,56 |
| 11 | Параболоид | 68,04 | 2567,5 | 3,79 | 2635,54 |
| 12 | Гиперболоид | 44,94 | 1696 | 2,53 | 1740,94 |
| Итого | 406,98 | 15358,5 | 25,82 | 15765,48 |
Проанализировав материальные затраты, можно сделать вывод, что стоимость сырья приемлемая, разориться на электроэнергии при 3D- печати достаточно сложно. Себестоимость напечатанных моделей на 97,4% определяется стоимостью затрат на оплату труда по созданию моделей геометрических фигур с использованием программы «Компас-3D». Но, поскольку я конструировал модели геометрических фигур сам и печатал их на школьном 3D-принтере, используя снова школьное программное обеспечение и компьютер, то можно сказать, что наглядное пособие по стереометрии достаточно бюджетное – 432,8 руб.
Сравнительный анализ цен
Теперь окунёмся в мир интернета и посмотрим на всё что я сделал с чисто прагматической, финансовой стороны. Как оказалось при производстве наглядных пособий по тематике геометрических фигур за основу взяты детские игровые наборы, пазлы, а для старшего поколения – это в основном красочная печатная продукция. Получается ничего серьёзного, только единичные предложения.
| Вид пособия | Количество фигур | Страна производства | Стоимость |
| 
| 10 | Китай | 576р. |
| 
| 7 | Россия | 906р. |
| 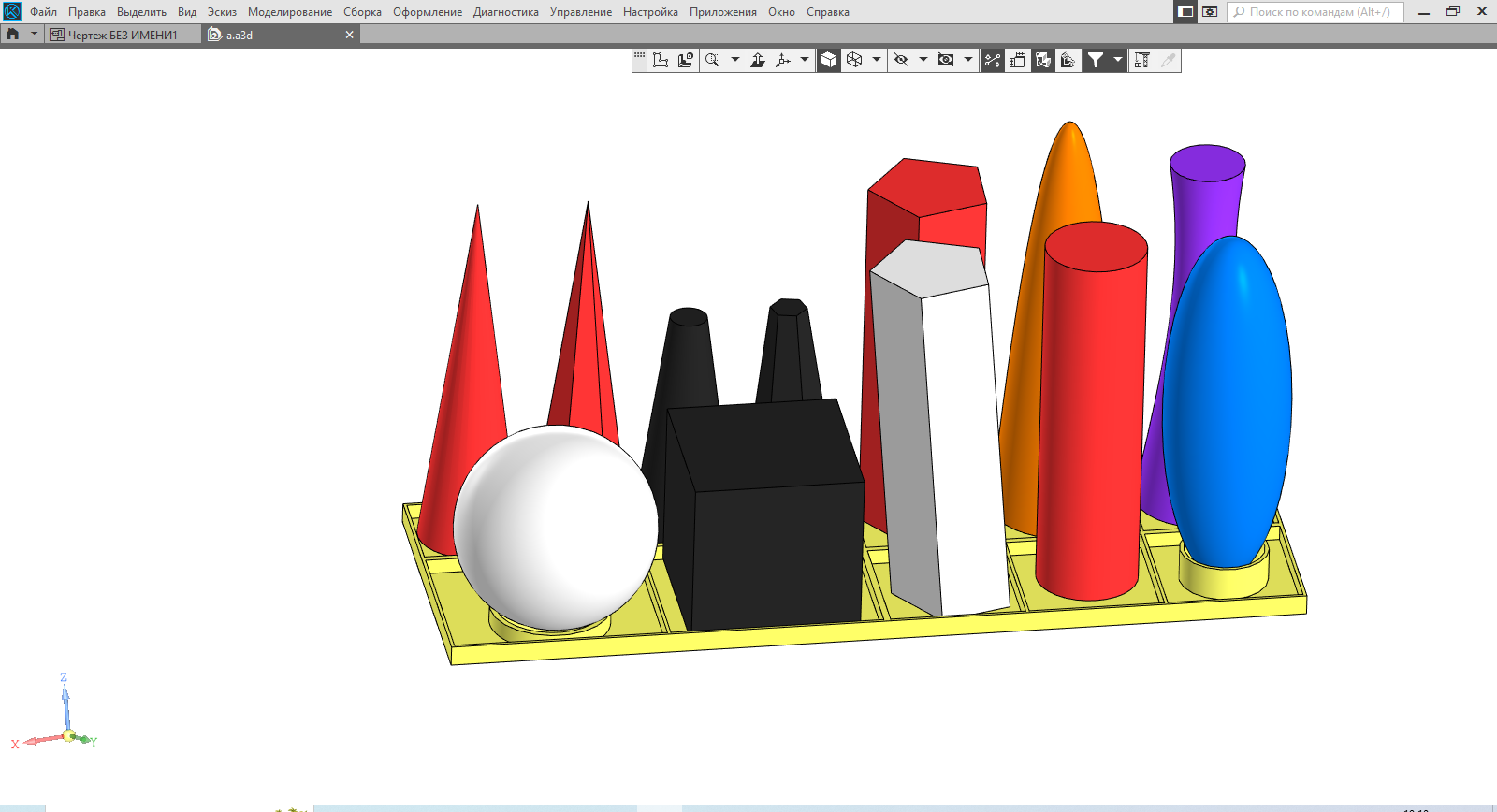
| 12 | Россия | 432,8р. |
Во всех случаях использован экологичный материал, вот только мой пластик более долговечен и безопасен. В моём наборе фигур больше, они разнообразнее и больше по размерам (особенно по сравнению с китайскими).
ЗАКЛЮЧЕНИЕ
Подводя итоги, могу с уверенностью сказать, что достоинства трехмерных технологий довольно ощутимы. Данная технология открыла двери в мир объемных изображений и деталей, которые нашли себе применение во многих сферах современной жизни, начиная от архитектуры и заканчивая промышленной отраслью. И можно сказать, что на этом возможности 3D-технологий не останавливаются, а развиваясь, идут в ногу со временем.
Работая над проектом, я постоянно встречался с различными сложными задачами, которые нужно было решать. Для этого понадобилось более глубокое изучение программы «Компас-3D». Мне стало понятно, что для создания 3D-моделей недостаточно простых навыков работы за компьютером. Использование программы «Компас-3D» требует колоссальных усилий, умения представлять предметы в пространстве и понимания, как они устроены, а также внимания и упорства. Я убедился, что занятие 3D-моделированием помогает развивать творческие способности, пространственное мышление и аккуратность, подтвердив гипотезу проекта.
Таким образом, собрав информацию об объёмных геометрических фигурах, изучив в школе программу «Компас-3D», применив фантазию и потратив некоторое время и средства, я создал методом 3D-печати наглядное пособие по стереометрии - собственный набор для изучения геометрических тел – отличный «помощник» на уроках геометрии, как в электронном виде, так и в напечатанном на 3D-принтере.
Пройдя такой путь, смело могу сказать, что увлечение 3D-моделированием возможно повлияет на выбор моей будущей профессии.
СПИСОК ИНФОРМАЦИОННЫХ ИСТОЧНИКОВ
Самоучитель КОМПАС-3D V20 / А.И. Герасимов. — Санкт-Петербург: BHV-СПб, 2022. — 656 с.
Проектирование в системе КОМПАС: учеб. пособие для студентов технических специальностей / Н.И. Жарков, А.И. Вилькоцкий, О.В. Ярошевич. — Минск: БГТУ, 2006. — 148 с.
http://wwwkompas-edu.ru. Методические материалы размещены на сайте «КОМПАС в образовании».
https://ascon.ru Сайт фирмы АСКОН.
3D моделирование что это и для чего нужно? Электронный ресурс. Режим доступа: https://dekormyhome.ru/remont-i-oformlenie/3d-modelirovanie-v-sovremennom-dizaine-interera.html
Что такое 3д моделирование, или как мечты превратить в реальность. Электронный ресурс. Режим доступа: https://websoftex.ru/3d-modelirovanie-chto-eto-i-dlya-chego-nuzhno/
[Электронный ресурс]. – URL: http://all-flesh.ru/story/3d-modelirovanie-v-21-vek
[Электронный ресурс]. – URL: https://ru.readkong.com/page/lekciya-34-poverhnosti-2-go-poryadka-7793211
[Электронный ресурс]. – URL: https://3dtoday.ru/blogs/3Dtool/help-a-lot-of-beginners-repetierhost-first-steps-part-1
ПРИЛОЖЕНИЕ













 Полигональное моделирование нужно не только для творческих людей (художников, дизайнеров, скульпторов). Еще одной крупной сферой применения 3D моделей является медицина, а именно – хирургия. Можно вырастить протез кости взамен раздробленной. Конечно, используя полигональное моделирование, можно построить все восстанавливающие и усиливающие элементы, но невозможно контролировать необходимые зазоры, сечения, учесть физические свойства материала и технологию изготовления (особенно плечевого сустава). Для таких изделий применяются методы
Полигональное моделирование нужно не только для творческих людей (художников, дизайнеров, скульпторов). Еще одной крупной сферой применения 3D моделей является медицина, а именно – хирургия. Можно вырастить протез кости взамен раздробленной. Конечно, используя полигональное моделирование, можно построить все восстанавливающие и усиливающие элементы, но невозможно контролировать необходимые зазоры, сечения, учесть физические свойства материала и технологию изготовления (особенно плечевого сустава). Для таких изделий применяются методы 
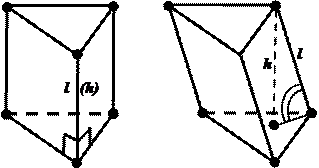

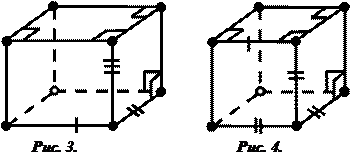

 У
У
 сечённой пирамидой называется многогранник, заключённый между основанием пирамиды и секущей плоскостью, параллельной её основанию (Рис.12).
сечённой пирамидой называется многогранник, заключённый между основанием пирамиды и секущей плоскостью, параллельной её основанию (Рис.12).





 стороной 50 мм и окружность Ø30 мм (Рис. 18).
стороной 50 мм и окружность Ø30 мм (Рис. 18). 
 Затем используем частный случай элемента выдавливания – элемент вращения и придаём объём. Отрезок, проведённый через центр окружности, послужил осью вращения. Получаем шар (Рис. 21).
Затем используем частный случай элемента выдавливания – элемент вращения и придаём объём. Отрезок, проведённый через центр окружности, послужил осью вращения. Получаем шар (Рис. 21). Рис.22. Эскиз прямоугольника
Рис.22. Эскиз прямоугольника Рис.23. Цилиндр
Рис.23. Цилиндр
 Следующая фигура вращения – конус. Здесь всё отличие в контуре вращения. В цилиндре – прямоугольник, в конусе прямоугольный треугольник. Построим эскиз прямоугольного треугольника со сторонами: 50 мм – высота конуса, 30 мм – радиус окружности основания (Рис. 24). Используя элемент вращения, получаем объёмную геометрическую фигуру – конус (Рис. 25).
Следующая фигура вращения – конус. Здесь всё отличие в контуре вращения. В цилиндре – прямоугольник, в конусе прямоугольный треугольник. Построим эскиз прямоугольного треугольника со сторонами: 50 мм – высота конуса, 30 мм – радиус окружности основания (Рис. 24). Используя элемент вращения, получаем объёмную геометрическую фигуру – конус (Рис. 25).

 Продолжаем строить конус, ещё один вариант. Вспомним последний вариант построения цилиндра. Отредактируем его и получим снова конус. Открываем в программе цилиндр, построенный вращением прямоугольника, и редактируем эскиз прямоугольника (Рис. 28).
Продолжаем строить конус, ещё один вариант. Вспомним последний вариант построения цилиндра. Отредактируем его и получим снова конус. Открываем в программе цилиндр, построенный вращением прямоугольника, и редактируем эскиз прямоугольника (Рис. 28). 

 Построим объёмную геометрическую фигуру – пирамиду. Из вышеописанного можно сделать выводы: построение сложной пирамиды возможно при использовании автоматического построения многогранника, лежащего в её основании.
Построим объёмную геометрическую фигуру – пирамиду. Из вышеописанного можно сделать выводы: построение сложной пирамиды возможно при использовании автоматического построения многогранника, лежащего в её основании. 

 Следующий вариант построения пирамиды основан на уже известном методе использования смещённых плоскостей и формирование объёма элементом по сечениям. В одной плоскости – многоугольник, в другой – точка (Рис. 33). Используем элемент по сечениям и получаем пирамиду (Рис. 34).
Следующий вариант построения пирамиды основан на уже известном методе использования смещённых плоскостей и формирование объёма элементом по сечениям. В одной плоскости – многоугольник, в другой – точка (Рис. 33). Используем элемент по сечениям и получаем пирамиду (Рис. 34).
 сечение конуса и пирамиды просто и одинаково, по сути. Используется метод смещённых плоскостей. Сам процесс отсечения производится командой «сечение» в разделе «элементы тела». Один нюанс: при усечении рядом стоящих объектов на разных высотах, необходимо в опциях сечения выбирать конкретное тело (Рис. 35).
сечение конуса и пирамиды просто и одинаково, по сути. Используется метод смещённых плоскостей. Сам процесс отсечения производится командой «сечение» в разделе «элементы тела». Один нюанс: при усечении рядом стоящих объектов на разных высотах, необходимо в опциях сечения выбирать конкретное тело (Рис. 35).



 алее с помощью команды формирования объёма – элемента выдавливания, а именно его частного случая, элемента вращения – получаем объёмную фигуру эллипсоида (Рис. 40). В разделе меню «моделирование» есть очень полезная команда масштабировать, которую я использую для изменения размеров (Рис. 41) эллипсоида, причём по каждой оси можно задавать свой коэффициент масштаба.
алее с помощью команды формирования объёма – элемента выдавливания, а именно его частного случая, элемента вращения – получаем объёмную фигуру эллипсоида (Рис. 40). В разделе меню «моделирование» есть очень полезная команда масштабировать, которую я использую для изменения размеров (Рис. 41) эллипсоида, причём по каждой оси можно задавать свой коэффициент масштаба.

 ычислять точки, а просто многократно изменяя коэффициенты масштаба, добиться необходимого внешнего вида.
ычислять точки, а просто многократно изменяя коэффициенты масштаба, добиться необходимого внешнего вида.


 иперболоид. Построение аналогично предыдущим с некоторым нюансом. На эскизе (Рис. 45) по точкам строим одну из ветвей гиперболы. При использовании элемента вращения, ось вращения строится в процессе создания объёма под вполне логичным углом в 45 или по вектору с координатами точек (0;0) и (0,5;0,5) (Рис. 46).
иперболоид. Построение аналогично предыдущим с некоторым нюансом. На эскизе (Рис. 45) по точкам строим одну из ветвей гиперболы. При использовании элемента вращения, ось вращения строится в процессе создания объёма под вполне логичным углом в 45 или по вектору с координатами точек (0;0) и (0,5;0,5) (Рис. 46). 















