У

 чебный элемент
чебный элемент
Тема: «Объёмный и содержательный подходы к измерению информации.» - 11 -
П редмет: «Информатика»
редмет: «Информатика»
Цели:
Изучив данный учебный элемент, Вы узнаете:
об алфавитном (объёмном) подходе к измерению информации;
о содержательном подходе к измерению информации;
о вероятности и информации;
о примерах решения задач по данной теме;
Оборудование, материалы и вспомогательные средства:
персональный компьютер;
мультимедиа проектор;
презентация урока;
раздаточный материал.
Сопутствующие учебные элементы и пособия:
Учебник И.Г. Семакин и др.
Как можно измерить информацию? Определить её объём.
Существуют два подхода в измерении количества информации: алфавитный (объёмный) и вероятностный (содержательный)
1. Алфавитный подход к определению количества информации
Алфавитный подход позволяет определить количество информации, заключенной в тексте.
Алфавит: все буквы, цифры, знаки препинания, скобки, пробел, специальные знаки.
Полное число символов в алфавите называют мощностью алфавита - N.
В алфавитном подходе: каждый символ алфавита имеет определённый информационный вес – i.
Информационный вес символа зависит от мощности алфавита.
Двоичный алфавит имеет самую маленькую мощность, так как состоит всего из двух символов: 0 и 1.
Информационный вес символа двоичного алфавита принят за единицу информации и называется 1 бит.
Итак, информационный вес каждого символа (i) и мощность алфавита (N) связаны формулой:
2i=N (формула Хартли)
Информационный объём (I) текста, содержащего К символов:
I = К * i
Максимального размера алфавита не существует, но есть достаточный. Его мощность равна 256 символов.
N=256; 256=2i, ; i=8, т.е. один символ этого алфавита весит 8 бит. Его назвали байт.
1 байт = 8 бит
Пример:
мощность русского алфавита равна 54: 33 буквы +10 цифр + 11 знаков препинания + скобки + пробел.
N – количество символов (возможных событий)
i (бит) информации несёт каждый символ
2i=N N=54 ð i= 5,755 бит
Значит, 1 символ русского алфавита несёт 5,755 бит информации
| i | N |
| 1 | 21 = 2 |
| 2 | 22 = 4 |
| 3 | 23 = 8 |
| 4 | 24 = 16 |
| 5 | 25 = 32 |
| 6 | 26 = 64 |
| 7 | 27 = 128 |
| 8 | 28 = 256 |
| 9 | 29 = 512 |
| 10 | 210 = 1024 |
Пример
Найти объём информации книги, сделанной с помощью текстового редактора, если она содержит 150 страниц, на каждой странице – 40 строк, в каждой строке – 60 символов.
Решение
1 страница содержит: 40*60=2400 байт информации.
Книга: 2400 байт*150=360 000 байт.


2. Содержательный подход к измерению информации
Содержательный подход – сущность состоит в том, что количество информации связывается с содержанием сообщения.
1 бит информации несёт сообщение, уменьшающее неопределённость знания в два раза.
Неопределённость знания о результате некоторого события – это количество возможных результатов.
Метод поиска, на каждом шаге которого отбрасывается половина вариантов, называется методом половинного деления.
Пример.
На книжном стеллаже восемь полок. Книга может быть положена на любую из них.
Сколько информации содержит сообщение о том, где находится книга?
Решение
Вопрос №1: книга лежит выше 4 полки?
Ответ: нет.
1 2 3 4 5 6 7 8 (1 бит)
Вопрос №2: книга лежит ниже 3 полки?
Ответ: да.
1 2 3 4 (1 бит)
Вопрос №3: книга на 2 полке?
Ответ: нет.
1 2 (1 бит)
Итог: книга лежит на 1 полке.
1 (3 бита)
Сообщение об одном из двух равновероятностных результатов некоторого события несёт 1 бит информации.
Количество информации i, содержащейся в сообщении о том, что произошло одно из N равновероятностных событий, определяется из решения показательного уравнения:
N = 2i - главная формула информатики
Если N – целая степень числа, то решение простое. Если N=8, то 8=2i , 23 =2i , значит i=3
Если N – нецелая степень числа? У кубика 6 граней:
Если N=6, то 6 =2i , поэтому i – дробное число. 2 i
значит i = 2,58496
Таблица. Количество информации в сообщении об одном из N равновероятностных событий.
| N | i | N | i |
|
|
| 1 | 0.00000 | 11 | 3.45943 |
| 2 | 1.00000 | 12 | 3.58496 |
| 3 | 1.58496 | 13 | 3.70044 |
| 4 | 2.00000 | 14 | 3.80735 |
| 5 | 2.32193 | 15 | 3.90689 |
| 6 | 2.58496 | 16 | 4.00000 |
| 7 | 2.80735 | 17 | 4.08746 |
| 8 | 3.00000 | 18 | 4.16993 |
| 9 | 3.16993 | 19 | 4.24793 |
| 10 | 3.32193 | 20 | 4.32193 |





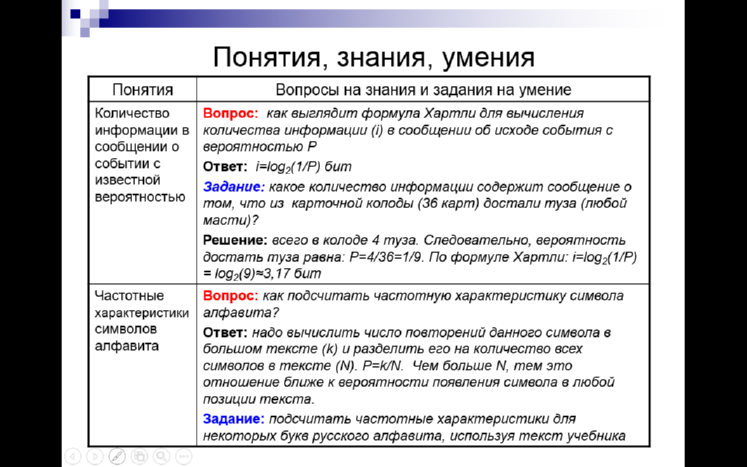
Примеры решения задач
Задача 1
Одно племя имеет 32-символьный алфавит, а второе племя – 64-символьный алфавит. Вожди племен обменялись письмами. Письмо первого племени содержало 80 символов, а письмо второго племени – 70 символов. Сравните объем информации, содержащийся в письмах.
| Дано: N1 = 32 ; N2 = 64 К1 = 80; К2 = 70 I1 - ? I2 - ?
| Решение I1 = K 1∙ i1; I2 = K 2∙ i2 2i = N 2i = 32; i1= 5 бит 2i = 64; i2 = 6 бит I1 = 5 ∙ 80 = 400 бит; I2 = 6 ∙ 70 = 420 бит Ответ: I2 I1
|
Задача 2
Информационное сообщение объемом 1,5 Кб содержит 3072 символа. Сколько символов содержит алфавит, при помощи которого было записано это сообщение?
| Дано: I = 1,5 Кб K = 3072 N - ?
| Решение: N = 2i ; I = K ∙ i i = I / K I = 1,5 ∙ 1024 ∙ 8 = 12288 бит i = 12288 / 3072 = 4 бита N = 24 = 16 символов Ответ: 16 символов |
Задача 3
Для записи сообщения использовался 64-символьный алфавит. Каждая страница содержит 30 строк. Все сообщение содержит 8775 байт информации и занимает 6 страниц. Сколько символов в строке?
| Дано: N = 64 I = 8775 байт Кол. стр. = 6 Кол. строк = 30 K - ?
| Решение: I = K ∙ i K = I / i N = 2i I = 8775 байт = 8775 ∙ 8 = 70 200 бит 64 = 2i , i = 6 бит I одной стр. = I / кол-во страниц = 70200 бит / 6 = 11700 бит K = 11700 бит/ 6 бит / 30 строк = 65 символов Ответ: K = 65 символов |
Задача 4
Считая, что каждый символ кодируется одним байтом, определите, чему равен информационный объем следующего высказывания Жан-Жака Руссо: Тысячи путей ведут к заблуждению, к истине – только один.
| Дано: i = 1 байт = 8 бит K = 57 I - ?
| Решение: I = K ∙ i I = K ∙ i = 1 ∙ 57 = 57 байт х 8 = 456 бит Ответ: I =456 бит |
Что такое «неопределенность знаний»? Рассмотрим примеры:
Пример 1: Вы бросаете монету, загадывая, что выпадет: орел или решка?
Решение: Есть два варианта возможного результата бросания монеты. Ни один из этих вариантов не имеет преимущества перед другим (равновероятны). Перед подбрасыванием монеты неопределенность знаний о результате равна двум.
После совершения действия неопределенность уменьшилась в 2 раза. Получили 1 бит информации.
Ответ: Результат подбрасывания монеты принес 1 бит информации.
Пример 2: Студент на экзамене может получить одну из четырех оценок: 5, 4, 3, 2. Учится неровно и с одинаковой вероятностью может получить любую оценку. После сдачи экзамена, на вопрос: «Что получил?» - ответил: «Четверку». Сколько бит информации содержится в его ответе?
Решение: Если сразу сложно ответить на вопрос, то можно отгадать оценку, задавая вопросы, на которые можно ответить только «да» или «нет», т.е. поиск осуществляется отбрасыванием половины вариантов.
Вопросы будем ставить так, чтобы каждый ответ уменьшал количество вариантов в два раза и, следовательно, приносил 1 бит информации.
1 вопрос: Оценка выше тройки? - ДА
(число вариантов уменьшилось в два раза.) Получен 1 бит информации.
2 вопрос: Ты получил пятерку? - НЕТ
(выбран один вариант из двух оставшихся: оценка – «четверка».) Получен еще 1 бит.
В сумме имеем 2 бита.
Ответ:Сообщение о том, что произошло одно из четырех равновероятностных событий несёт 2 бита информации.
Самостоятельная работа
Задание 1
Два текста содержат одинаковое количество символов. Первый текст составлен в алфавите мощностью 16 символов. Второй текст в алфавите мощностью 256 символов. Во сколько раз количество информации во втором тексте больше, чем в первом?
Задание 2
Мощность алфавита равна 256. Сколько Кбайт памяти потребуется для сохранения 160 страниц текста, содержащего в среднем 192 символа на каждой странице?
Задание 3
Сколько различных последовательностей длиной в 7 символов можно составить из цифр 0 и 1?
Задание 4
Объем сообщения равен 11 Кбайт. Сообщение содержит 11264 символа. Какова мощность алфавита?
Контрольные вопросы
Сущность объёмного подхода к измерению информации
Определение бита с алфавитной точки зрения
Связь между размером алфавита и информационным весом символа
Связь между единицами измерения: бит, байт, Кбайт, Мбайт, Гбайт
Сущность содержательного подхода информации
Определение бита с позиции содержания сообщения.

Иванилова Т.С.
Липецкий политехнический техникум









 чебный элемент
чебный элемент редмет: «Информатика»
редмет: «Информатика»

















