Функция. Область определения и область значений функции - Функции и их свойства - Квадратичная функция
Цель: рассмотреть понятие функции и способы лостроения функции
Ход урока
I. Сообщение темы и цели урока
II. Изучение нового материала
Эта тема является одной из важнейших для всего курса математики. Различные функции будут изучаться вплоть до окончания школы и далее в высших учебных заведениях. Пока же вы познакомитесь с самыми простыми функциями - линейными, квадратичными, дробно-линейными и другими функциями и их графиками. Также вы получите первое представление о графиках уравнений и неравенств.
Данная тема вплотную связана с решением уравнений, неравенств, текстовыми задачами и т. д. Поэтому обратите самое серьезное внимание на ее изучение. Особое внимание следует уделить развитию навыков построения графиков функций, уравнений, неравенств.
1. Понятие функции
Пусть даны два множества действительных чисел D и Е и указан закон f по которому каждому числу х ∈ D ставится в соответствие единственное число у ∈ Е (см. рис.). Тогда говорят, что задана функция y = f(х) с областью определения (О.О.) D и областью значений (О.З.) Е. При этом величину х называют независимой переменной (или аргументом функции), величину у - зависимой переменной (или значением функции).
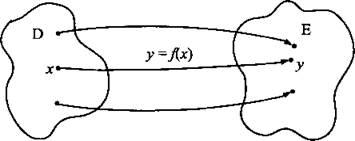
Область определения у = f(x) обозначают D(f), область значений E(f).
Другими словами, функцией называют такую зависимость переменной у от переменной х, при которой каждому значению переменной х соответствует единственное значение переменной у.
Пример 1
Рассмотрим функцию 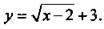 Для нахождения у для каждого значения х необходимо выполнить следующие операции: от величины х вычесть число 2 (x - 2), извлечь квадратный корень из этого выражения
Для нахождения у для каждого значения х необходимо выполнить следующие операции: от величины х вычесть число 2 (x - 2), извлечь квадратный корень из этого выражения 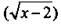 и, наконец, прибавить число 3
и, наконец, прибавить число 3 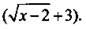 Совокупность этих операций (или закон, по которому для каждого значения х ищется величина y) и называется функцией y(x). Например, для х = 6 находим
Совокупность этих операций (или закон, по которому для каждого значения х ищется величина y) и называется функцией y(x). Например, для х = 6 находим 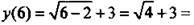
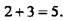 То есть для вычисления функции у в данной точке х необходимо подставить эту величину x в данную функцию у(х).
То есть для вычисления функции у в данной точке х необходимо подставить эту величину x в данную функцию у(х).
Очевидно, что для данной функции для любого допустимого числа х можно найти только одно значение у (т. е. каждому значению х соответствует одно значение y).
Рассмотрим теперь область определения и область значений этой функции. Извлечь квадратный корень из выражения (х - 2) можно только, если эта величина неотрицательная, т. е. х - 2 ≥ 0, или х ≥ 2. Поэтому О.О. функции D(y) = [2; +∞). Так как по определению арифметического корня 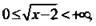 то прибавив ко всем частям этого неравенства число 3, получим
то прибавив ко всем частям этого неравенства число 3, получим 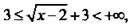 или 3 ≤ у
или 3 ≤ у
Пример 2
Зависимость 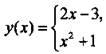 уже не является функцией. Действительно, если мы хотим вычислить значение у, например, для х = 1, то, пользуясь верхней формулой, найдем у = 2 · 1 - 3 = -1, а пользуясь нижней формулой, получим у = 12 + 1 = 2. Таким образом, одному значению х (х = 1) соответствуют два значения у (у = -1 и у = 2). Поэтому эта зависимость (по определению) не является функцией.
уже не является функцией. Действительно, если мы хотим вычислить значение у, например, для х = 1, то, пользуясь верхней формулой, найдем у = 2 · 1 - 3 = -1, а пользуясь нижней формулой, получим у = 12 + 1 = 2. Таким образом, одному значению х (х = 1) соответствуют два значения у (у = -1 и у = 2). Поэтому эта зависимость (по определению) не является функцией.
Пример 3
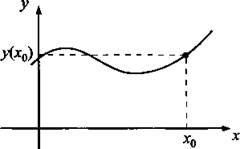
Приведены графики двух зависимостей у(х). Определить, какая из них является функцией.
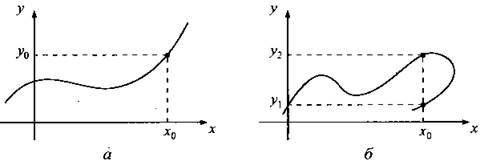
На рис. а приведен график функции, т. к. любой точке х0 соответствует только одно значение На рис. б приведен график какой-то зависимости (но не функции), т. к. существуют такие точки (например, х0), которым отвечает более одного значения у (например, значения y1 и у2).
2. Способы задания функций
1) Аналитический (с помощью формулы или формул)
Пример 4
Рассмотрим функции.
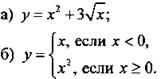
Несмотря на непривычную форму, это соотношение также задает функцию. Для любого значения х легко найти величину у. Например, для х = -0,37. Так как х 0, то пользуемся нижним выражением) имеем: 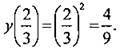 Из способа нахождения у понятно, что любой величине х отвечает только одно значение у.
Из способа нахождения у понятно, что любой величине х отвечает только одно значение у.
в) 3х + у = 2у – х2. Выразим из этого соотношения величину у: 3х + х2 = 2у - у, или х2 + 3х = у. Таким образом, это соотношение также задает функцию у = х2 + 3х.
2) Табличный
Пример 5
Выпишем таблицу квадратов y для чисел х.
| x | 1 | 1,5 | 2 | 2,5 | 3 | 4 | 5 | 6 | 7 |
| y | 1 | 2,25 | 4 | 6,25 | 9 | 16 | 25 | 36 | 49 |
Такая таблица также задает функцию: для каждого (приведенного в таблице) значения x можно найти единственное значение у. Например, y(1,5) = 2,25, y(5) = 25 и т. д.
3) Графический
В прямоугольной системе координат для изображения функциональной зависимости y(x) удобно пользоваться специальным рисунком - графиком функции.
Графиком функции y(x) называют множество всех точек системы координат, абсциссы которых равны значениям независимой переменной х, а ординаты - соответствующим значениям зависимой переменной у.
В силу такого определения все пары точек (x0, у0), которые удовлетворяют функциональной зависимости y(x), расположены на графике функции. Любые другие пары точек, не удовлетворяющие зависимости y(x), на графике функции не лежат.
Пример 6
Дана функция у = 2х - 3|x| + 4. Принадлежит ли графику этой функции точка с координатами: а) (-2; -6); б) (-3; -10)?
а) Найдем значение функции у при х = -2: у(-2) = 2 · (-2) - 3|-2| + 4 = -4 – 3 · 2 + 4 = -6. Так как у(-2) = -6, то точка А(-2; -6) принадлежит графику данной функции.
б) Определим значение функции у при x = -3: y(-3) = 2 · (-3) - 3|-3| + 4 = -6 – 3 · 3 + 4 = -11. Так как у(-3) = -11, то точка В(-3; -10) не принадлежит графику этой функции.
Сравним различные способы задания функции. Наиболее полным следует считать аналитический способ. Этот способ позволяет составить таблицу значений функции для некоторых значений аргументов, построить график функции, провести необходимое исследование функции. Вместе с тем табличный способ позволяет быстро и легко найти значение функции для некоторых значений аргумента. График функции наглядно показывает ее поведение. Поэтому противопоставлять различные способы задания функции не следует: каждый из них имеет свои преимущества и свои недостатки. На практике используются все три способа задания функции.
В дальнейшем будем считать основным аналитический способ задания функции и рассмотрим еще несколько задач.
Пример 7
Дана функция у = 2x2 – 3x + 1. Найти: а) у(2); б) y(-3х); в) у(х + 1).
Для того чтобы найти значение функции при каком-то значении аргумента, необходимо подставить это значение аргумента в аналитический вид функции. Поэтому получим:
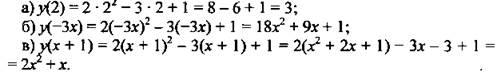
Пример 8
Известно, что у(3 - x) = 2x2 - 4. Найти: а) у(х); б) у(-2).
а) Обозначим буквой z = 3 - x, тогда х = 3 - z. Подставим это значение х в аналитический вид данной функции у(3 - х) = 2х2 - 4 и получим: у(3 - (3 - z))2 - 4, или y(z) = 2 · (3 - z)2 - 4, или y(z) = 2 · (9 - 6z + z2) - 4, или y(z) = 2z2 - 12z + 14. Так как безразлично, какой буквой обозначен аргумент функции: z, х, t или любой другой, то сразу получаем: у(х) = 2x2 – 12x + 14.
б) Теперь легко найти у(-2) = 2 · (-2)2 – 12 · (-2) + 14 = 8 + 24 + 14 = 46.
III. Контрольные вопросы
1. Дайте определение функции и поясните примером.
2. Что такое область определения и область значений функции? Приведите примеры.
3. Перечислите основные способы задания функций.
IV. Задание на уроке
№ 1; 4; 5 (a); 6 (б); 7; 9 (а, в, е); 10; 12; 14 (a); 15.
V. Задание на дом
№ 2; 3; 5 (б); 6 (a); 8; 9 (б, г, д); 11; 13; 14 (б); 16.
VI. Творческие задания
1. Найдите область определения функции.

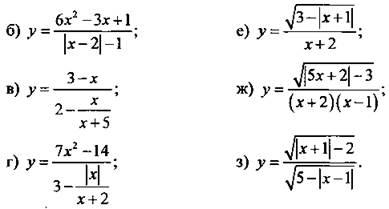
Ответы: 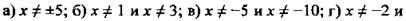
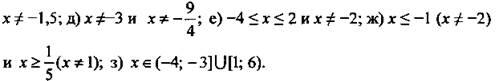
2. Известно значение функции у(6 - х). Найдите функцию у(х).
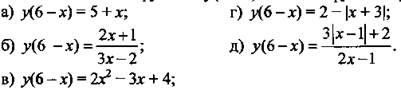
Ответы: 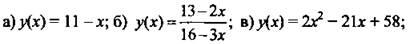
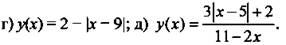
3. Известно значение функции у(2х - 4). Найдите функцию y(x).
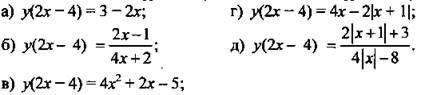
Ответы: 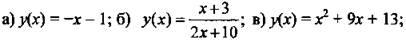
VII. Подведение итогов урока
Свойства и графики основных функций - Функции и их свойства - Квадратичная функция
Цель: вспомнить изученные ранее функции и их свойства.
Ход урока
I. Сообщение темы и цели урока
II. Повторение и закрепление пройденного материала
1. Ответы на вопросы по домашнему заданию (разбор нерешенных задач).
2. Контроль усвоения материала (самостоятельная работа).
Вариант 1
1. Найдите значения функции у(-2) · y(1).
2. Найдите область определения функции.
Вариант 2
1. Найдите значения функции у(-3) · у(2).
2. Найдите область определения функции.
III. Изучение нового материала
1. Свойства функции
Как уже известно из курса 7-8 классов, любая функция характеризуется определенными свойствами. Часть этих свойств была рассмотрена ранее. Теперь необходимо систематизировать эти свойства и рассматривать их при исследовании любых функций и построении их графиков.
Остановимся теперь на свойствах функции. С двумя свойствами функции вы уже знакомы - это область определения и область значений функции. Рассмотрим следующее свойство функции - точка пересечения графика функции с осями координат.
Так как ось Оу характерна тем, что любая точка на ней имеет координату х = 0, а для оси Ох - любая точка на ней имеет координату у = 0, то точки пересечения графика с осями координат ищутся очень просто. Точка пересечения с осью Оу равна значению функции у(х) при х = 0, т. е. у(0). Точки пересечения с осью Ох являются корнями уравнения у(х) = 0 и называются нулями функции.
Пример 1
Рассмотрим функцию у(х) = -х2 + 6х - 8.
Найдем точки пересечения графика этой функции с осями координат. Чтобы определить точку пересечения графика с осью ординат, вычислим значение функции y(х) при х = 0: у(0) = -02 + 6 · 0 - 8 = -8. Получаем координаты этой точки A(0; -8).
Теперь определим точки пересечения графика данной функции с осью абсцисс. Для этого в функцию у = -х2 + 6х - 8 подставим значение у = 0 и получим квадратное уравнение 0 = -х2 + 6х - 8, или 0 = х2 - 6х + 8.
Решим его:
Поэтому график функции пересекает ось абсцисс в двух точках: В(2; 0) и С(4; 0). Для наглядности на рисунке приведен график данной функции (здесь мы несколько забежали вперед) Следующее свойство - ограниченность функции. Функция называется ограниченной снизу, если все значения функции не меньше некоторого числа а (т. е. у(х) ≥ а). Функция называется ограниченной сверху, если все значения функции не больше некоторого числа А (т. е. y(x) ≤ А). Если функция ограничена снизу и сверху, то она называется ограниченной. На рисунке приведены графики ограниченных и неограниченных функций.
Следующее свойство - ограниченность функции. Функция называется ограниченной снизу, если все значения функции не меньше некоторого числа а (т. е. у(х) ≥ а). Функция называется ограниченной сверху, если все значения функции не больше некоторого числа А (т. е. y(x) ≤ А). Если функция ограничена снизу и сверху, то она называется ограниченной. На рисунке приведены графики ограниченных и неограниченных функций.
Для выяснения ограниченности функции очень часто используются алгебраические преобразования.
Пример 2
Докажем, что функция y(x) = -х2 + 6х - 8 ограничена сверху.
Выделим в функции y(x) = -(x2 - 6х + 8) полный квадрат разности. Для этого в скобках прибавим и вычтем единицу.
Получаем: у(х) = -(х2 - 6х + 8) = -((х2 - 6х + 9) — 1) = -((х - 3)2 - 1) = 1 - (х - 3)2.
Так как при всех значениях х величина (х - 3)2 ≥ 0, величина -(х - 3)2 ≤ 0, то 1 - (х - 3)2 ≤ 1, т. е. у(х) ≤ 1. Тогда по определению данная функция ограничена сверху (при этом число А, входящее в определение, равно 1). Из графика примера 1 наглядно видно, что при всех значениях x значения у(х) ≤ 1.
Рассмотрим еще одно свойство функции - монотонность (т. е. возрастание или убывание функции). Функция называется возрастающей, если большему значению аргумента соответствует большее значение функции (т. е. если х2 х1, то у(х2) y(x1)). Функция называется убывающей, если большему значению аргумента соответствует меньшее значение функции (т. е. если х2 x1, то у(х2)
Пример 3
На рисунке приведены графики монотонных (возрастающей и убывающей) и немонотонной функции

Определитьмонотонность функции у(х) = -2х + 4.
Область определения этой функции - все значения х, т. е. х ∈ (-∞; +∞). Возьмем два значения х из области определения этой функции х1 и х2 и пусть х2 х1. Найдем значения функции в этих точках: y(х1) = -2х1 + 4 и у(х2) = -2х2 + 4. Теперь необходимо сравнить эти значения и определить, какое из них больше. Для этого рассмотрим разницу этих величин: у(х2) - y(x1) = (-2х2 + 4) - (-2x1 + 4) = -2х2 + 4 + 2x1 - 4 = -2(х2 – x1).
Так как х2 x1, то разность х2 – x1 0 и величина -2(х2 - x1)
Функция во всей области определения может быть немонотонной, но на отдельных промежутках функция может быть монотонной. Например, в примере 1 функция в целом немонотонная, но на промежутке х ∈ [3; +∞) функция убывает, а на промежутке х ∈ (-∞; 3] - возрастает (докажите самостоятельно).
И наконец, рассмотрим еще одно свойство функции - четность. Предварительно введем еще одно понятие - симметричность области определения. Область определения называется симметричной, если функция определена и в точке х0, и в точке (-х0) (т. е. в точке, симметричной х0 относительно начала числовой оси).
Пример 4
а) Областью определения функции являются все значения х, кроме тех, для которых х2 - 4 = 0 (т. е. х = ±2). Поэтому эта функция определена, например, как при х = -1, так и при х = -(-1) = 1.
И наоборот, эта функция не определена и при х = -2, и при х = -(-2) = 2. Следовательно, область определения данной функции х ∈ (-∞; -2)U(-2; 2)U(2; +∞) симметричная.
б) Областью определения функции являются все значения х, кроме тех, для которых х - 4 = 0 (т. е. х = 4). Поэтому эта функция определена в точке x = -4, но не определена в симметричной точке x = -(-4) = 4. Поэтому область определения данной функции x ∈ (-∞; 4)U(4; +∞) не является симметричной.
Понятие четности функции вводится только для функции с симметричной областью определения. Функция называется четной, если при изменении знака аргумента, значение функции не меняется, т. е. y(-х) = у(х). График четной функции всегда симметричен относительно оси ординат.
Функция называется нечетной, если при изменении знака аргумента, значение функции также меняется на противоположное, т. е. у(-х) = -у(х). График нечетной функции всегда симметричен относительно начала координат.
На рисунке приведены (для наглядности) графики четной, нечетной функции и функции, не имеющей никакой четности.

Пример 5
Выяснить четность функций: а) у = |х| - x2; б) у = x - x3; в) y = x - 2.
Прежде всего отметим, что области определения всех трех функций х ∈ (-∞; +∞) симметричны. Для выяснения четности этих функций y(x) надо найти значение y(-x) и сравнить значения y(x) и y(-x).
а) y(-x) = |-x| - (-x)2 = |x| - х2 (здесь учтено, что |-х| = |x| и (-х)2 = x2). Теперь легко видеть, что y(-x) совпадает с данной функцией y(x), т. е. y(-x) = y(x). Поэтому данная функция четная и ее график симметричен относительно оси ординат.
б) y(-х) = -x - (-x)3 = -х - (-х)3 = -х + х3 = -(х - х3) = -у(х). Видно, что значения функции в точках х и -х противоположны по знаку, т. е. y(-x) = -y(x). Поэтому данная функция нечетная и ее график симметричен относительно начала координат.
в) y(-x) = -х - 2. Сравнивая значение –y(x) = -х - 2 со значением y(x) = х - 2, видим, что равенство y(-x) = y(x) не выполняется. Поэтому эта функция не является четной. Найдем теперь величину –y(x) = -(х - 2) = 2 - x. Сравнивая значение y(-x) = -x - 2 со значением –y(x) = 2 - x, видим, что равенство y(-x) = -y(x) также не выполняется. Поэтому эта функция не является нечетной.
Итак, данная функция никакой четности не имеет и ее график не обладает никакой симметрией.
В заключение отметим, что исследование основных свойств функции облегчает анализ ее поведения и построение ее графика. В старших классах будут рассмотрены и другие свойства функции.
2. Свойства и графики некоторых функций
Теперь необходимо вспомнить основные свойства и графики некоторых ранее изученных функций (свойства надо представлять, но запоминать не стоит).
Линейная функция у = kx + b
1. Область определения - множество всех чисел.
2. Графиком функции является прямая линия.
3. График функции пересекает ось абсцисс в точке х = b/k (при k ≠ 0) и параллелен оси абсцисс при k = 0. График функции пересекает ось ординат в точке у = b.
4. Функция возрастает при k 0, убывает при k
5. Функция неограниченная при k ≠ 0 и ограниченная при k = 0.
6. Функция определенной четности не имеет при b ≠ 0, нечетная при b = 0 и четная при k = 0.
7. Область значений - множество всех чисел при k ≠ 0 и у = b при k = 0.
8. При b = 0 функцию у = kх называют прямой пропорциональной
Пример 6
Найти условие, при котором линейная функция у = kх + b является: а) нечетной; б) четной.
Область определения функции х ∈ (-∞; +∞) — симметричная. Найдем значение у(-x) = k · (-х) + b = -kх + b.
а) Если функция нечетная, то у(-x) = -y(x). Получаем: -kх + b = -(kх + b), или b = -b, или 2b = 0, откуда b = 0.
б) Если функция четная, то у(-x) = y(x). Получаем: -kх + b = kх + b, или 0 = 2kх, откуда k = 0 (т. к. x - любое число, не равное нулю).
Обратная пропорциональность у = k/x.
1. Область определения - множество всех чисел, кроме нуля.
2. Графиком функции является гипербола.
3. График функции осей координат не пересекает.
4. Функция возрастает при k 0 в области определения.
5. Функция неограниченная.
6. Функция нечетная.
7. Область значений - множество всех чисел, кроме нуля.
Пример 7
Выясним монотонность обратной пропорциональности у = k/x.
Область определения данной функции D(y) = (-∞; 0)U(0; +∞). Рассмотрим два произвольных значения x1 и х2 (где x1 х2) из области определения функции. Найдем значения функции в этих точках y(x1) = k/x1 и у(х2) = k/x2 и сравним их. Для этого рассмотрим разность Так как х2 х1, то разность x1 - х2 отрицательна. Поэтому знак разности у(х2) — у(х1) противоположен знаку дроби k/x1x2.
Функция у = k/x не определена в точке х = 0. Рассмотрим два промежутка области определения. При х1, х2 ∈ (-∞; 0) и при х1 ,х2 ∈ (0; +∞) произведение x1x2 положительно. Поэтому знак разности у(х2) — у(х1) противоположен знаку коэффициента k. Следовательно, при k 0. т. е. у(х2) у(х1) и функция возрастает; при k 0 величина у(х2) — у(х1)
Квадратная функция у = х2
Заметим, что функция у = х2 является частным случаем квадратичной функции, которая детально будет изучаться позднее.
1. Область определения - множество всех чисел.
2. Графиком функции является парабола.
3. График функции проходит через начало координат.
4. Функция убывает на промежутке (-∞; 0] и возрастает на промежутке [0; +∞).
5. Функция ограничена снизу, т. е. у ≥ 0.
6. Функция четная.
7. Область значений - промежуток [0; +∞).
Пример 8
Докажем ограниченность квадратичной функции у = х2.
Очевидно, что при всех значениях x величина у = х2 принимает только неотрицательные значения, т. е. у ≥ 0. По определению функция ограничена снизу, т. е. у ≥ а (где а может быть любым неположительным числом: a = -103, a = -5, a = -0,1, a = 0).
Кубическая функция у = x3
1. Область определения - множество всех чисел.
2. График специального названия не имеет.
3. График функции проходит через начало координат.
4. Функция возрастает.
5. Функция неограниченная.
6. Функция нечетная.
7. Область значений - множество всех чисел.
Пример 9
Ads by optAd360
Докажем нечетность кубической функции у = х3.
Область определения функции х ∈ (-∞; ∞) - симметричная. Найдем значение функции у(-х) = (-х)3 = (-1)3 · х3 = -х3 = -y(x). Так как выполнено равенство у(-х) = y(x), то по определению данная функция нечетная.
Функция 
1. Область определения — множество неотрицательных чисел.
2. График специального названия не имеет.
3. График выходит из начала координат.
4. Функция возрастает.
5. Функция ограничена снизу, т. е. у ≥ 0.
6. Функция определенной четности не имеет.
7. Область значений - множество неотрицательных чисел.
Функция = |x|
1. Область определения - множество всех чисел.
2. График специального названия не имеет.
3. График проходит через начало координат.
Ads by optAd360
4. Функция убывает на промежутке (-∞; 0] и возрастает на промежутке [0; +∞).
5. Функция ограничена снизу, т. е. у ≥ 0.
6. Функция четная.
7. Область значений - множество неотрицательных чисел.
Рассмотренные свойства функций используются и при построении графиков более сложных функций.
Пример 10
Построим график функции 
Область определения функции - множество всех чисел, кроме х = 2. Сократим дробь и запишем функцию в виде  Поэтому надо построить график линейной функции у = 2 - 2х и удалить из него точку с абсциссой х = 2 (показана стрелками).
Поэтому надо построить график линейной функции у = 2 - 2х и удалить из него точку с абсциссой х = 2 (показана стрелками).
Пример 11
Построим график функции у = 2х + |х - 3|.
Раскроем знак модуля, рассмотрев два случая. При х - 3 Строим при х
IV. Контрольные вопросы
1. Как найти точки пересечения графика функции с осями координат?
2. Понятие ограниченности функции.
3. Возрастающая и убывающая на промежутке функция.
4. Нечетная и четная функции и их свойства.
5. Свойства и график линейной функции y = kх + b.
6. Свойства и график обратной пропорциональности у = k/x.
Ads by optAd360
7. Свойства и график квадратичной функции у = х2.
8. Свойства и график кубической функции y = х3.
9. Свойства и график функции 
10. Свойства и график функции у = |х|.
V. Задание на уроке
№ 17 (а, в); 18 (а); 20; 23; 25 (а); 27; 29 (а); 30 (а, в, д); 31 (а, г); 32; 37; 41 (б); 42 (а); 45; 51 (а); 53 (б); 54 (а).
VI. Задание на дом
№ 17 (б, г); 18 (б); 21; 22; 25 (б); 28; 29 (б); 30 (б, г, е); 31 (б, в); 33; 38; 41 (в); 42 (б); 46 (а); 51 (б); 53 (в); 54 (б, в).
VII. Творческие задания
1. Постройте график функции:
2. Постройте множество точек (х; у), координаты которых удовлетворяют условию:
VIII. Подведение итогов урока
Корни квадратного трехчлена - Квадратный трехчлен - Квадратичная функция
Цель: рассмотреть понятие квадратного трехчлена, его корни, выделение квадрата двучлена.
Ход урока
I. Сообщение темы и цели урока
II. Повторение и закрепление пройденного материала
1. Ответы на вопросы по домашнему заданию (разбор нерешенных задач).
2. Контроль усвоения материала (письменный опрос).
Вариант 1
1. Функция, возрастающая на промежутке.
2. Понятие нечетной функции и ее свойство.
3. Постройте график функции.
Вариант 2
1. Функция, убывающая на промежутке.
2. Понятие четной функции и ее свойство.
3. Постройте график функции.
III. Изучение нового материала
Выражение (где х - переменная;  - коэффициенты, при этом аn ≠ 0) называют многочленом n-й степени. Коэффициент аП называют старшим коэффициентом, коэффициент а0 - свободным членом.
- коэффициенты, при этом аn ≠ 0) называют многочленом n-й степени. Коэффициент аП называют старшим коэффициентом, коэффициент а0 - свободным членом.
Ads by optAd360
Пример 1
а) - многочлен пятой степени, а5 = 2 - старший коэффициент, а0 = -5 - свободный член.
б) — многочлен третьей степени, а3 = 7 - старший коэффициент, а0 = 0 - свободный член.
Значение переменной x0, при котором многочлен Рn(х) равен нулю, называют корнем многочлена, т. е. Рn(х0) = 0.
Пример 2
Найдем корни многочлена Р3(х) = 2х3 - 8х.
Для этого необходимо решить кубическое уравнение 2х3 - 8х = 0. Разложим левую часть уравнения на множители: 2х(х2 - 4) = 0, или 2х(х + 2)(х - 2) = 0. Произведение множителей равно нулю, если один из них равен нулю.
Получаем три линейных уравнения: х = 0, х + 2 = 0, х - 2 = 0, откуда x1 = 0, х2 = -2 и х3 = 2.
Итак, данный многочлен имеет три корня.
Наиболее изучен и наиболее часто встречается в школьном курсе математики многочлен второй степени - квадратный трехчлен. Квадратным трехчленом называют многочлен ах2 + bх + с, где х - переменная, а, b и с — коэффициенты (а ≠ 0). Коэффициент а называют старшим коэффициентом, b - вторым коэффициентом, с - свободным членом.
Пример 3
а) Р2(х) = 3х2 - 7х - 2 - квадратный трехчлен, у которого а = 3, b = -7 и с = -2.
б) Р2(х) = 3х2 - 1х - квадратный трехчлен, у которого а = 3, b = -7 и с = 0.
в) Р2(х) = 3х2 - квадратный трехчлен, у которого а = 3, b = с = 0.
Таким образом, может оказаться, что в квадратном трехчлене коэффициенты b = 0, или с = 0, или даже b = с = 0.
Естественно, чтобы найти корни квадратного трехчлена Р2(х) = ах2 + bх + с, надо решить квадратное уравнение Р2(х) = 0.
Ads by optAd360
Дискриминант D = b2 - 4ас квадратного уравнения Р2(х) = 0 также считают дискриминантом квадратного трехчлена Р2(х). Если D 0, то квадратный трехчлен имеет два различных корня: если D = 0 - один корень (точнее, два одинаковых корня); если D
Найдем корни квадратного трехчлена 3х2 - 5х - 2.
Решим квадратное уравнение 3х2 - 5х - 2 = 0.
Для этого уравнения а = 3, b = -5 и с = -2. Найдем дискриминант D = (-5)2 - 4 · 3 · (-2) = 49 и корни т. е. х1 = 12/6 = 2 и x2 = -2/6 = -1/3.
Итак, данный трехчлен имеет два корня х1 = 2 и х2 = -1/3.
Подобным же образом можно находить и корни квадратных трехчленов с параметром (в основном однородных трехчленов).
Пример 5
Найдем корни квадратного трехчлена 4х1 – 3nх – 7n2 (где n - параметр).
Данный трехчлен является однородным, т. к. каждый из его членов: 4х2, -3nх и -7n2 - имеет одну и ту же (вторую) степень. Решим однородное квадратное уравнение 4х2 – 3nх – 7n2 = 0. Для этого уравнения а = 4, b = -3n и с = -7n2. Найдем дискриминант и корни  т. е. х1 = 14n/8 = 7/4n и и х2 = -8n/8 = -n. Таким образом, данный трехчлен имеет два корня: х1 = 7n/4 и х2 = -n.
т. е. х1 = 14n/8 = 7/4n и и х2 = -8n/8 = -n. Таким образом, данный трехчлен имеет два корня: х1 = 7n/4 и х2 = -n.
При решении задач удобно бывает квадратный трехчлен aх2 + bх + с представить в виде а(х - m)2 + n, где m и n - некоторые числа. Такое преобразование называют выделением квадрата двучлена из квадратного трехчлена.
Пример 6
Выделим из трехчлена 2х2 - 16х + 7 квадрат двучлена.
Сначала вынесем за скобки коэффициент 2 и получим: Теперь в скобках выделим квадрат двучлена. Для этого представим член -8х в виде удвоенного произведения: -8х = -2· х · 4. Затем прибавим и вычтем квадрат второго члена 42. Получаем:
Таким образом, из квадратного трехчлена 2х2 - 16х + 7 выделили квадрат двучлена 2(х - 4)2 - 25, т. е. представили в заданном виде (где а = 2, m = 4 и n = -25).
В частности, такое представление позволяет утверждать, что наименьшее значение трехчлена равно -25 и достигается при х = 4. Действительно, в выражении 2(х - 4)2 - 25 при всех х величина 2(х - 4)2 ≥ 0. Поэтому наименьшее значение выражения будет при х - 4 = 0, т. е. х = 4.
Аналогичный прием может быть использован и при исследовании многочленов второй степени с двумя переменными.
Пример 7
Найдем наименьшее значение многочлена Р(х, у) = 2х2 + у2 + 2ху - 2х + 5.
В данном многочлене представим члены в виде: 2х2 = х2 + х2 и 5 = 1 + 4 и выделим квадраты двучленов. Получаем.
Учтем, что при всех значениях х и у величины (х + у)2 ≥ 0 и (х - 1)2 ≥ 0. Поэтому наименьшее значение данного многочлена достигается при условии х + у = 0 и х - 1 = 0, т. е. при х = 1 и y = -1. Это наименьшее значение равно 4.
Выделение квадрата двучлена полезно использовать и при решении прикладных задач.
Пример 8
На берегу канала надо огородить с трех сторон участок прямоугольной формы (со стороны канала участок не загораживают) наибольшей площади. Длина забора 120 м. Каковы будут размеры участка и его площадь?
Пусть забор имеет форму ломаной ABCD со сторонами АВ = CD = х (м) и ВС = 120 - 2х (м). Найдем площадь участка S = АВ · ВС = х(120 - 2х) = -2х2 + 120х (м2). Выделим в этом квадратном трехчлене квадрат двучлена: S = -2х2 + 120х = -2(х2 - 60х) = -2(х2 - 2 · х · 30 + 302 - 302) = -2(х - 30)2 + 2 · 900 = 1800 - 2(х - 30)2. При всех значениях х выражение -2(х - 30)2 ≤ 0. Поэтому величина S имеет наибольшую величину при х = 30, и эта величина S = 1800. Таким образом, размеры забора равны: АВ = 30 м, ВС = 60 м и CD = 30 м. При этом площадь участка составляет 1800 м2 (18 соток).
IV. Контрольные вопросы
1. Какое выражение называют многочленом n-й степени с одной переменной?
2. Корень многочлена n-й степени.
3. Какой многочлен называют квадратным трехчленом?
4. Как найти корни квадратного трехчлена?
5. Сколько корней имеет квадратный трехчлен?
6. Какое преобразование называют выделением квадрата двучлена из квадратного трехчлена?
V. Задание на уроке
№ 55; 56 (а, г); 59 (а, б, д, е); 61 (а, г); 63; 64 (а, в); 66 (б, г); 68; 70; 72; 74(a); 75 (б).
VI. Задание на дом
№ 56 (б, в); 58; 59 (в, г); 61 (б, в); 64 (б, г); 66 (а, в); 69; 71; 73; 74 (б); 75 (а).
VII. Творческие задания
1. Найдите связь между переменными хи^, если выполнено равенство.
Ответы: а) х = 2,5у и х = -4у; б) х = 4у и х = 1/3у; в) х = 5у и х = 1,5у; г) х = у и х = 0,6y.
2. Найдите наибольшее значение выражения. При каких значениях х и у оно достигается?
Ответы: а) 13 при х = -2 и у = 3; б) 29 при х = 5 и y = -1; в) 7 при х = 1 и y = -1; г) 10 при х = 2 и у = 2.
3. Найдите наибольшее значение выражения. При каких значениях х и у оно достигается?
Ответы: а) 7 при х = 2 и у = -3; б) 1 при х = 1 и у = -2; в) 10 при х = -2 и у =3; г) 2 при х = 1 и у = 5.
VIII. Подведение итогов урока
Разложение квадратного трехчлена на множители - Квадратный трехчлен - Квадратичная функция
Цель: обсудить разложение многочленов на линейные множители.
Ход урока
I. Сообщение темы и цели урока
II. Повторение и закрепление пройденного материала
1. Ответы на вопросы по домашнему заданию (разбор нерешенных задач).
2. Контроль усвоения материала (письменный опрос).
Вариант 1
1. Дайте определение многочлена n-й степени.
2. Найдите корни квадратного трехчлена 3х2 - 5х - 2.
3. Найдите наименьшее значение выражения х2 + у2 - 6х + 8у.
Вариант 2
1. Дайте определение квадратного трехчлена.
2. Найдите корни квадратного трехчлена 7х2 - 4х - 3.
3. Найдите наименьшее значение выражения х2 + у2 + 4х - 8у.
III. Изучение нового материала
При решении уравнений, действиях с алгебраическими дробями и т. д. необходимо раскладывать многочлены на множители. Особенно часто приходится раскладывать квадратные трехчлены на линейные множители. При этом необходимо учитывать две следующие теоремы.
Теорема 1. Если х1 и х2 - корни квадратного трехчлена ах2 + bх + с, то ах2 + bх + с = а(х – х1)(х - х2).
Докажем это утверждение. В многочлене ах2 + bх + с вынесем за скобки множитель а и получим: Учтем, что х1 и х2 корни и квадратного трехчлена ах2 + bх + с, и квадратного уравнения ах2 + bх + с = 0. Поэтому по теореме Виета тогда
Подставив эти соотношения, получим: 

В таком равенстве раскроем скобки, сгруппируем слагаемые и разложим выражение на множители: 

Итак, получили: и тогда
Заметим, что в этом выражении многочлены х – х1 и х - х2 имеют первую степень, т. е. линейные многочлены. Поэтому равенство является разложением квадратного трехчлена ах2 + bх + с на линейные множители х – x1 и х - х2 (с точностью до коэффициента а).
Пример 1
Разложим на линейные множители квадратный трехчлен 4х2 - 3х - 10.
Найдем корни этого трехчлена, решив квадратное уравнение 4х - 3х- 10 = 0. Такими корнями являются числа х1 = -5/4 и х2 = 2.
Тогда по доказанной теореме получаем: 
Такое разложение можно записать и в другом виде, внеся множитель 4 в первую скобку: 4х2 - 3х - 10 = (4х + 5)(х - 2).
Пример 2
Разложим на множители квадратный трехчлен -3х2 + 12х - 12.
Решив квадратное уравнение -3х2 + 12х - 12, найдем два равных корня трехчлена: x1 = х2 = 2.
Тогда получаем разложение данного квадратного трехчлена на множители: -3х2 + 12х - 12 = -3(х - 2)(х - 2), или -3х2 + 12х - 12 = -3(х - 2)2.
Таким образом, теорема 1 выполняется, если квадратный трехчлен имеет два различных или одинаковых корня, т. е. при дискриминанте трехчлена D ≥ 0.
Пример 3
Сократим дробь
Разложим на множители числитель и знаменатель дроби.
Корни числителя х1 = 1/2 и x2 = 5/3. Поэтому получаем: 
Корни знаменателя х1 = 1/2 и x2 = -1/4. Имеем разложение:  Теперь легко сократить дробь:
Теперь легко сократить дробь:
Обсудим теперь ситуацию, при которой квадратный трехчлен не имеет корней, т. е. его дискриминант D
Теорема 2. Если квадратный трехчлен ах2 + bх + с не имеет корней, то его нельзя разложить на множители, являющиеся многочленами первой степени.
Докажем способом от противного. Предположим, что квадратный трехчлен можно разложить на линейные множители, т. е. где k, m, р, q - некоторые числа и k ≠ 0, р ≠ 0.
Очевидно, что произведение (kx + m)(px + q) обращается в нуль при  . Следовательно, при таких значениях обращается в нуль и трехчлен ах2 + bх + с. Поэтому числа
. Следовательно, при таких значениях обращается в нуль и трехчлен ах2 + bх + с. Поэтому числа  являются корнями трехчлена ах2 + bх + с. Но это противоречит условию теоремы: трехчлен ах2 + bх + с корней не имеет.
являются корнями трехчлена ах2 + bх + с. Но это противоречит условию теоремы: трехчлен ах2 + bх + с корней не имеет.
Пример 4
Дискриминант квадратного трехчлена 3х2 - 5х + 4 равен: Так как дискриминант отрицательный, то квадратный трехчлен 3х2 - 5х + 4 корней не имеет и не может быть разложен на линейные множители.
Заметим, что способ разложения на линейные множители, изложенный в примерах 1-3, может быть использован и в случае многочленов второй степени с параметром.
Пример 5
Разложим на множители многочлен  (где n - параметр).
(где n - параметр).
Найдем корни данного трехчлена. Для этого решим квадратное уравнение В этом уравнении коэффициенты: а = 1, b = -3n и с = 2n2 + n - 1.
Найдем дискриминант и его корни т. е.
Теперь разложим многочлен на множители: 

Теорема 1 может быть обобщена и на случай многочлена n-й степени: если х1, х2, ..., хn - корни многочлена 
 то его можно разложить на линейные множители:
то его можно разложить на линейные множители:
Пример 6
Рассмотрим кубический многочлен Р3(х) = 3х3 + 4х2 - 5х - 2.
Проверкой можно убедиться, что он имеет корни х1 = -1/3, х2 = 1 и х3 = -2 (как найти эти корни - другой вопрос). Тогда многочлен можно разложить на линейные множители:
Заметим, что многочлен может не иметь корней, но тем не менее раскладываться на множители.
Пример 7
Разложим на множители многочлен четвертой степени Р4(х) = х4 + х2 + 1.
Очевидно, что такой многочлен корней не имеет. Действительно, при всех значениях х выражения х4 ≥ 0 и х2 ≥ 0. Поэтому значения многочлена Р4(х) ≥ 1 и не равны нулю.
Тем не менее его удается разложить на множители. Для этого к нему прибавим и вычтем х2, получим разность квадратов и разложим ее на множители. Имеем: 
Таким образом, многочлен четвертой степени разложили на произведение двух квадратных трехчленов. Очевидно, что разложить данный многочлен на линейные множители изначально было невозможно.
IV. Контрольные вопросы
1. Сформулируйте и докажите теорему о разложении на линейные множители квадратного трехчлена с неотрицательным дискриминантом.
2. Сформулируйте и докажите теорему о невозможности разложения на множители квадратного трехчлена с отрицательным дискриминантом.
V. Задание на уроке
№ 76 (а, б, г); 79 (а); 80 (б, г); 82; 83 (а, в, д); 85 (а); 87 (а); 88 (б).
VI. Задание на дом
№ 76 (в, д, и); 79 (б); 80 (а, в); 81; 83 (б, г, е); 85 (б); 87 (б); 88 (а).
VII. Творческие задания
1. Разложите на множители квадратный трехчлен.
Ответы:
2. Разложите на множители многочлен.
Ответы:
3. Найдите значение выражения.
Ответы: a-г) 0.
4. Разложите выражение на множители.
Ответы:
VIII. Подведение итогов урока
Функция y = ах2, ее график и свойства - Квадратичная функция и ее график - Квадратичная функция
Цель: рассмотреть свойства и график простейшей квадратичной функции у = ах2.
Ads by optAd360
Ход урока
I. Сообщение темы и цели урока
II. Повторение и закрепление пройденного материала
1. Ответы на вопросы по домашнему заданию (разбор нерешенных задач).
2. Контроль усвоения материала (самостоятельная работа).
Вариант 1
1. Разложите многочлен на множители.
2. Сократите дробь.
Вариант 2
1. Разложите многочлен на множители.
2. Сократите дробь.
III. Изучение нового материала
Одной из наиболее распространенных и изученных функций является квадратичная функция у = ах2 + bх + с, где х - независимая переменная; а, b и с- некоторые числа (причем а ≠ 0).
Например, перемещение х тела при движении с ускорением а описывается квадратичной функций где x0 и V0 - положение и скорость тела в начальный момент времени t = 0.
С частным случаем квадратичной функции у = х2 (где а = 1, b = 0, с = 0) школьники уже знакомы. Графиком этой функции является парабола. Продолжим изучение квадратичных функций. Сначала ограничимся изучением функции у = ах2.
Пример 1
Составим таблицу значений и в одной системе координат построим графики функций
| x | -2 | -1,5 | -1 | -0,5 | 0 | 0,5 | 1 | 1,5 | 2 |
| у = 1/2х2 | 2 | 1,12 | 0,5 | 0,12 | 0 | 0,12 | 0,5 | 1,12 | 2 |
| у = х2 | 4 | 2,25 | 1 | 0,25 | 0 | 0,25 | 1 | 2,25 | 4 |
| y = 2х2 | 8 | 4,5 | 2 | 0,5 | 0 | 0,5 | 2 | 4,5 | 8 |
Отметив на координатной плоскости точки, приведенные в таблице, построим графики данных функций. Видно, что при каждом значении х значения функции у = 1/2х2 в два раза меньше значений функции у = х2, а значения функции у = 2х2 в два раза больше значений функции у = х2. Другими словами, график функции у = 1/2х2 можно получить сжатием в два раза вдоль оси ординат графика функции у = х2. График функции у = 2х2 можно получить растяжением в два раза вдоль оси ординат графика функции у = х2.
Ads by optAd360
Вообще говоря, график функции у = ах2 можно получить из параболы у = х2 растяжением вдоль оси ординат в а раз при а 1 и сжатием вдоль оси ординат в 1/a раз при 0
Приведем свойства функции у = ах2 при а 0:
1. Область определения функции - промежуток (-∞; ∞).
2. Если х = 0, то у = 0. Следовательно, график проходит через начало координат.
3. Если х ≠ 0, то у 0. Поэтому график расположен в верхней полуплоскости.
4. Функция четная, т. е. противоположным значениям аргумента соответствуют равные значения функции у(-х) = у(х). График функции симметричен относительно оси ординат.
5. Функция убывает в промежутке (-∞; 0] и возрастает в промежутке [0; ∞).
6. Функция ограничена снизу, у ≥ 0. Наименьшее значение у = 0 функция принимает при х = 0, наибольшего значения функция не имеет.
7. Область значений функции - промежуток [0; +∞).
Ads by optAd360
Обсудим теперь свойства и график квадратичной функции у = ах2 при a
Пример 2
Составим таблицу значений и в одной системе координат построим графики функций у = 1/2х2 и у = -1/2х2.
| x | -2 | -1,5 | -1 | -0,5 | 0 | 0,5 | 1 | 1,5 | 2 |
| у = 1/2х2 | 2 | 1,12 | 0,5 | 0,12 | 0 | 0,12 | 0,5 | 1,12 | 2 |
| у = -1/2х2 | -2 | -1,12 | -0,5 | -0,12 | 0 | -0,12 | -0,5 | -1,12 | -2 |
Отметим точки, приведенные в таблице, и построим графики данных функций. Видно, что при каждом значении х значения функции у = -1/2х2 противоположны по знаку значениям функции у = 1/2х2. Поэтому график функции у = -1/2х2 получается из графика функции у = 1/2х2 с помощью симметрии относительно оси абсцисс.
Теперь легко сформулировать свойства функции у = ах2 при а
1. Область определения функции - промежуток (-∞; ∞).
2. Если х = 0, то у = 0. Следовательно, график проходит через начало координат.
3. Если х ≠ 0, то у
4. Функция четная, у(-х) = y(x). График функции симметричен относительно оси ординат.
5. Функция возрастает в промежутке (-∞; 0] и убывает в промежутке [0; ∞).
6. Функция ограничена сверху, у ≤ 0. Наибольшее значение у = 0 функция принимает при х = 0, наименьшего значения функция не имеет.
7. Область значений функции - промежуток (-∞; 0].
Пример 3
Обсудим монотонность функции у(х) = ах2.
Область определения такой функции - все значения х. Рассмотрим два произвольных значения х2 и х1, такие, что х2 x1. Найдем значения функции в этих точках: у(х2) = ах22 и у(х1) = ах12 и сравним их. Для этого определим знак разности у(х2) - у(х1) = ах22 – ах12 = а(х2 + х1)(х2 – х1).
Так как х2 x1, то разность х2 – х1 положительна. Поэтому разность у(х2) - у(х1) определяется знаком произведения а(х2 + х1). Так как сумма х2 + х1 может иметь различный знак, то в области определения выделим два промежутка.
а) Для промежутка х ∈ [0; +∞) сумма х2 + х1 0. Поэтому знак разности у(х2) - y(х1) совпадает со знаком коэффициента а.
При а 0 разность у(х2) - y(x1) 0, т. е. у(х2) у(х1) и функция возрастает.
При а
б) Для промежутка х ∈ (-∞; 0] сумма х2 + x1
При а 0 разность у(х2) - y(х1)
При а 0 разность у(х2) - y(х1) 0, т. е. у(х2) y(х1) и функция возрастает.
Ads by optAd360
Пример 4
Построим график функции
Область определения функции задается условием 2х - 4 ≠ 0, т. е. х ≠ 2. Разложим числитель и знаменатель дроби на множители и сократим ее. Получаем:
Построим параболу у = 1/2х2 и удалим из нее точку с абсциссой х = 2 (показана стрелками).
Пример 5
При каких значениях а парабола у = -1/2х2 и прямая у = 3х + а не имеют общих точек?
Предположим, что данные линии имеют общую точку. Тогда ее координаты удовлетворяют системе уравнений
Попробуем решить эту систему. Так как в уравнениях левые части одинаковы, то равны и правые.
Получаем уравнение -1/2х2 = 3х + а, или 0 = х2 + 6х + 2а. На самом деле данные линии общих точек не имеют. Это означает, что полученное квадратное уравнение решений не имеет. Поэтому его дискриминант D = 36 - 8а 36/8 = 4,5.
На рисунке приведена иллюстрация задачи. Очевидно, прямая у = 3х + а пересекает ось ординат в точке у = а. При увеличении а прямая смещается вверх параллельно самой себе. Выполненные расчеты показывают, что прямая при а 4,5 не имеет общих точек с параболой (линия 3).
IV. Контрольные вопросы
1. Какая функция называется квадратичной?
2. Как называют график квадратичной функции?
3. Приведите основные свойства и график функции у = ах2 при а 0.
4. Приведите основные свойства и график функции у = ах2 при а
5. Как из графика функции у = x2 получить график функции у = ах2 при а 0.
V. Задание на уроке
№ 90; 92; 94; 96 (а, в); 97; 99; 101; 103 (а); 104 (а); 105.
VI. Задание на дом
№ 91; 93; 95; 96 (б, г); 98; 100; 102; 103 (б, в); 104 (б).
VII. Творческие задания
1. Постройте график функции.
2. Постройте график уравнения или неравенства.
VIII. Подведение итогов урока
Графики функций у = ах2 + n и у = а(х - m)2 - Квадратичная функция и ее график - Квадратичная функция
Цель: рассмотреть параллельный перенос графика функции.
Ход урока
I. Сообщение темы и цели урока
II. Повторение и закрепление пройденного материала
1. Ответы на вопросы по домашнему заданию (разбор нерешенных задач).
2. Контроль усвоения материала (письменный опрос).
Вариант 1
1. Приведите основные свойства и график функции у = ах2 при а 0.
2. Постройте график функции.
3. При каком значении а прямая у = х + а касается параболы y = 0,5x2?
Вариант 2
1. Приведите основные свойства и график функции у = ах2 при а
2. Постройте график функции.
3. При каком значении а прямая у = х - а касается параболы у = -2x2?
III. Изучение нового материала
На предыдущем уроке были рассмотрены два важнейших преобразования графика функции у = f(x).
1. График функции у = -f(x) получается из графика функции у = f(x) с помощью симметрии относительно оси абсцисс.
2. График функции у = af(x) получается из графика функции у = f(x) растяжением вдоль оси ординат в а раз при а 1 и сжатием в 1/a раз при 0
Эти преобразования пригодны для любых функций (как изученных, так и еще не рассмотренных). Поэтому необходимо знать такие преобразования и уметь ими пользоваться.
Рассмотрим еще два важнейших преобразования графика функции у = f(х) - построение графиков функции у = f(х) + n и y = f(x - m).
3. График функции у = f(x) + n получается из графика функции у = f(x) с помощью параллельного переноса вдоль оси ординат на |n| единиц: вверх при n 0 и вниз при n
Пример 1
Построим график функции у = -х2 - 2.
В соответствии с приведенным алгоритмом график функции у = -х2 - 2 получается из графика функции у = -x2 параллельным переносом вдоль оси ординат на 2 единицы вниз, т. к. n = -2
4. График функции у = f(x - m) получается из графика функции у = f(x) с помощью параллельного переноса вдоль оси абсцисс на |m| единиц: вправо при m 0 и влево при m
Ads by optAd360
Пример 2
Построим график функции у = (х + 1)2.
Запишем функцию в виде у = (х - (-1))2. Тогда в соответствии с изложенным алгоритмом график функции y = (х + 1)2 получается из графика функции у = х2 параллельным переносом вдоль оси абсцисс на 1 единицу влево, т. к. m = -1
Из преобразований 3-4 следует, что график функции у = f(x - m) + n получается из графика функции у = f(x) с помощью двух параллельных переносов: сдвига вдоль оси абсцисс на |m| единиц: вправо при m 0 и влево при m 0 и вниз при n
Пример 3
Построим график функции у = -1/2(х - 2)2 + 1.
Очевидна следующая последовательность преобразований графика (алгоритм построения):
Ads by optAd360
1. Строим график функции у = х2.
2. Получаем из него график функции у = -х2 (преобразование 1 - симметрия относительно оси абсцисс).
3. Строим график функции у = -1/2х2 (преобразование 2 - сжатие предыдущего графика в два раза вдоль оси ординат).
4. Получаем из него график функции у = -1/2х2 + 1 (преобразование 3 - сдвиг на одну единицу вверх).
5. Строим график функции у = -1/2(х - 2)2 + 1 (преобразование 4- сдвиг предыдущего графика на две единицы вправо).
После выполнения этих построений получаем окончательный график (на рисунке приведены: начальный этап построения - график функции у = х2 и конечный этап - график у = -1/2(х - 2)2 + 1).
IV. Контрольные вопросы
1. Алгоритм построения графика функции у = -f(x)?
2. Как построить график функции у = af(x) при а 0?
3. Построение графика функции у = f(x) + n.
4. Алгоритм построения графика функции у = f(x - m).
V. Задание на уроке
№ 106 (а, в); 107 (а); 109 (а, в, д); 110 (б, в); 114; 116 (а, в); 117 (а); 118 (а, б).
VI. Задание на дом
№ 106 (б, г); 107 (б); 109 (б, г, е); 110 (а, г); 115; 116 (б, г); 117 (б); 118 (в, г).
VII. Подведение итогов урока







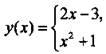 уже не является функцией. Действительно, если мы хотим вычислить значение у, например, для х = 1, то, пользуясь верхней формулой, найдем у = 2 · 1 - 3 = -1, а пользуясь нижней формулой, получим у = 12 + 1 = 2. Таким образом, одному значению х (х = 1) соответствуют два значения у (у = -1 и у = 2). Поэтому эта зависимость (по определению) не является функцией.
уже не является функцией. Действительно, если мы хотим вычислить значение у, например, для х = 1, то, пользуясь верхней формулой, найдем у = 2 · 1 - 3 = -1, а пользуясь нижней формулой, получим у = 12 + 1 = 2. Таким образом, одному значению х (х = 1) соответствуют два значения у (у = -1 и у = 2). Поэтому эта зависимость (по определению) не является функцией.
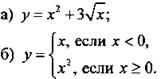

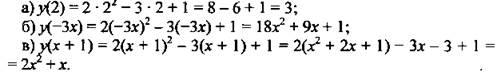

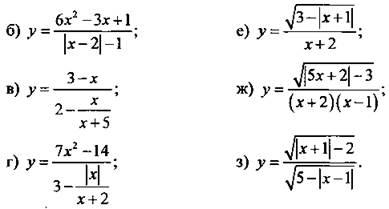
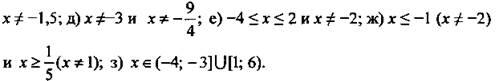
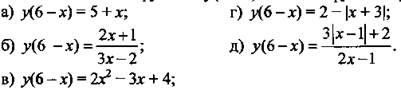
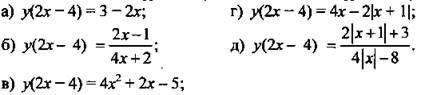
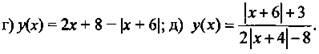
 Следующее свойство - ограниченность функции. Функция называется ограниченной снизу, если все значения функции не меньше некоторого числа а (т. е. у(х) ≥ а). Функция называется ограниченной сверху, если все значения функции не больше некоторого числа А (т. е. y(x) ≤ А). Если функция ограничена снизу и сверху, то она называется ограниченной. На рисунке приведены графики ограниченных и неограниченных функций.
Следующее свойство - ограниченность функции. Функция называется ограниченной снизу, если все значения функции не меньше некоторого числа а (т. е. у(х) ≥ а). Функция называется ограниченной сверху, если все значения функции не больше некоторого числа А (т. е. y(x) ≤ А). Если функция ограничена снизу и сверху, то она называется ограниченной. На рисунке приведены графики ограниченных и неограниченных функций.



















