Обобщающее повторение: решение геометрических задач по теме "Длина окружности и дуги. Площадь круга и его частей."

Длина окружности и дуги. Площадь круга и его частей.

1. Найдите площадь круга: а) описанного около прямоугольного треугольника с катетом а и противолежащим углом α; б) описанного около равнобедренного треугольника с основанием а и высотой h, проведенной к основанию; в) вписанного в равнобедренный треугольник с боковой стороной b и углом α при основании; г) описанного около равнобокой трапеции с основаниями 5 и 3 и боковой стороной 2.

2. Внутри круга радиуса r проходит окружность, которая делит его площадь пополам. Каков радиус этой окружности?

3. а) Квадрат и круг имеют одинаковую длину границы. Какая из этих фигур имеет большую площадь? б) Квадрат и круг равновелики. У какой из этих фигур длиннее граница?

4. В правильный многоугольник вписана окружность. Докажите, что отношение площади круга, ограниченного этой окружностью, к площади многоугольника равно отношению длины окружности к периметру многоугольника.

5. В кольце, образованном двумя концентрическими окружностями, хорда большей окружности, касающаяся меньшей, равна а. Определите площадь кольца.

6. Постройте круг, площадь которого равна: а) сумме площадей двух данных кругов;

б) площади данного кольца.

7. Найдите площадь кольца шириной d, если L — длина окружности, равноудаленной от его краев.

8. Каким способом выгоднее (с точки зрения расходов на материал) перекачивать газ: по одной большой трубе с площадью сечения S или по двум малым трубам с площадью сечения S/2 у каждой?

9. На сторонах прямоугольного треугольника как на диаметрах построены три полукруга. Докажите, что площадь полукруга, построенного на гипотенузе, равна сумме площадей полукругов, построенных на катетах.

10. Из точки С данной полуокружности опущен перпендикуляр CD на диаметр АВ, и на отрезках AD и DB как на диаметрах построены новые полуокружности по одну сторону с данной. Докажите, что площадь арбелоса Архимеда,— фигуры, ограниченной тремя полуокружностями,— равна площади круга с диаметром CD.

11. Найдите радиус сектора площади S с центральным углом 72°.

12. Какую часть от площади круга составляет площадь сектора, если: а) центральный угол сектора равен 300°; б) длина дуги сектора равна диаметру круга?

13. Вычислите площадь сектора, если известны: а) длина его дуги l и радиус круга R;

б) длина его границы т и центральный угол φ радиан.

14. АВ и CD — два взаимно перпендикулярных диаметра круга. Из точки D как из центра радиусом DA описана дуга АМВ (М— внутри круга). Докажите, что луночка АМВС равновелика треугольнику ABD.

15. Определите площадь сегмента, если: а) ограничивающая его хорда имеет длину а, а дуга содержит 240°; б) длина его хорды 2, а длина его стрелки √2 -1. (Стрелка сегмента — это часть диаметра круга, перпендикулярного его хорде, лежащая внутри сегмента).

16. В круге радиуса R проведены по одну сторону от центра две параллельные хорды, одна из которых стягивает дугу в 120°, а другая — в 60°. Определите площадь части круга, заключенной между хордами.

17. Хорда CD параллельна диаметру АВ. Определите площадь, заключенную между дугой CD и хордами АС и AD, если площадь круга равна q, а дуга CD содержит 120°.

18. Из точки границы круга проведены две взаимно перпендикулярные хорды, отсекающие сегменты площадью s каждый. Определите площадь оставшейся части круга.

19. Колесо радиуса R катится по прямой. Какова длина пройденного им пути, если оно сделало n оборотов?

20. Два зубчатых колеса сцепили между собой. Их радиусы R₁ и R₂. Первое из них сделало n₁ оборотов. Сколько оборотов сделало второе?

21. Лесной участок имеет форму круга. Чтобы обойти этот участок по опушке, идя со скоростью 4 км / ч, нужно затратить на 45 мин больше, чем для того, чтобы пересечь его по диаметру. Найдите длину опушки данного участка.

22. а) Переведите в радианную меру углы в 30°, 72°, 120°, 135°; б) Переведите в градусную меру углы, величина которых в радианах равна π/4; π/12; 3π/5; 4π/3; 2.

23. На катушку диаметром 1 см намотано 20 см ниток. На какую наименьшую длину можно удлинить нитку, чтобы она намоталась за целое число оборотов?

24. Окружность радиуса 2 см разогнута в дугу радиуса 5 см. Найдите градусную меру дуги.

25. Окружность радиуса 5 см разогнута в дугу окружности, содержащую 150°. Найдите радиус дуги.

26. Вокруг треугольника ABC, в котором АС = 6, ∟A = 70°, ∟C = 80°, описана окружность. Найдите длины меньших дуг, концами которых являются вершины треугольника

27. В прямоугольном треугольнике ABC ВС =12, ∟A = 60°. Найдите длину дуги окружности с центром в вершине С, касающейся гипотенузы АВ и заключенной внутри треугольника.

28. Найдите хорду, стягивающую дугу длиной 2π, если дуга содержит: а) 60°; б) 90°;

в) 120°.

29. В окружности длиной 24π см проведена хорда, равная 12 см. Найдите градусную меру меньшей дуги, стягиваемой хордой.

30. В единичной окружности проведены хорды длиной √2 и √3. Как относятся длины меньших дуг, стягиваемых этими хордами?

31. Дуга сегмента содержит 120° и имеет длину 6π. Определите длину наибольшей окружности, вписанной в этот сегмент.

32. Две касательные к окружности имеют длину l и образуют угол φ радиан. Найдите длину меньшей дуги окружности, заключенной между точками касания.

33. Дан отрезок АВ (рис. а). Вы хотите покороче попасть из А в В, двигаясь только по полуокружностям, диаметры которых лежат на АВ. Какой вы выберете путь: верхний или нижний?

34. Все окружности (рис. б-г) имеют радиус 1. Для каждого случая определите длину выделенной линии.

35. Даны две окружности радиусами R и r (R r). Центр меньшей окружности лежит на большей. Длина дуги меньшей окружности внутри большего круга равна L. Какова длина дуги большей окружности внутри меньшего круга?

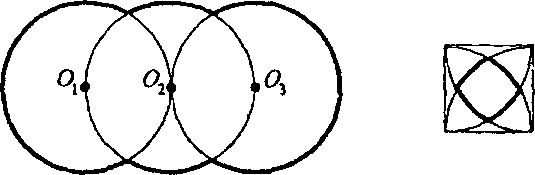
а) б) в) г).