Алгебра. Урок №75. 8 класс. Дата:____________________
Обобщающий урок. Системы уравнений.
Цели урока – обобщение и систематизация знаний учащихся по теме «Системы уравнений».
Задачи урока:
создать условия для обобщения, систематизации и развития знаний по теме «Системы уравнений», подготовить к контрольной работе;
создать условия для развития математического мышления, вычислительных и графических навыков, внимательности, устной и письменной математической речи;
воспитание культуры общения и поведения, аккуратности и трудолюбия, коммуникативных качеств личности.
Тип урока: урок обобщения и закрепления знаний, умений и навыков.
Структура урока.
I. Организационный момент.
Один из великих философов сказал: «Где есть желание – найдется путь!» Надеюсь, что вы сегодня на уроке с желанием будете решать системы, определяя свой рациональный путь.
II. Постановка целей и задач урока.
Итак, тема нашего урока – повторения «Системы уравнений». Запишите тему урока в тетради.
Скажите, какие цели вы поставите для себя на сегодняшний урок? Записать на доске.
- повторить, что такое системы уравнений, решение системы уравнений;
- вспомнить способы решения систем уравнений;
- вырабатывать умения в решении систем уравнений;…
У вас на столах лежат оценочные листы. За каждый этап урока выставляйте себе оценку.
III. Проверка домашнего задания.
Учащиеся сдают тетради с домашним заданием.
а) Страница 183 №7. Ответ: (3; 5); ( -1; -3)
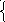 б) №9. у = 2 + х
б) №9. у = 2 + х
х2 + у2 = 10
х2 + (2 + х)2 = 10, х2 + 2х – 3 =0; D = 16; х1= 1; х2= - 3. Ответ: (1; 3); (-3; -1)
IV. Проверка теоретического материала в форме игры «Крестики-нолики».
Если вы согласны с утверждением, ставите крестик, если не согласны – нолик.
1. Решить систему уравнений, значит найти все ее решения или доказать, что решений нет.
2. Решением системы уравнений является пара чисел, обращающих в верное равенство хотя бы одно из уравнений.
3. Система уравнений может иметь бесконечно много решений.
4. Решить систему уравнений можно способом умножения.
5. Достоинство графического метода-наглядность.
6. Способ сложения предполагает исключение одной переменной.
7. Решить систему способом подстановки, это значить выразить только переменную у через х.
Самопроверка. Ответы: Х0Х0ХХ0. Не забываем выставлять оценки в оценочные листы.
V. Актуализация опорных знаний.
а) Выразите одну переменную через другую: 2х – 2у = 4; 7х – у = 1; х • у = 9 х2 + у – 9 = 0.
б) Является ли пара чисел (2; -1) решением системы?
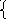
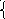
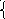 х + у = -1 х + у =1; х – у = 3;
х + у = -1 х + у =1; х – у = 3;
х – 2у = 6. нет 4х – 3у = 11. да 2х + у = 3. да
в) Установите соответствие между формулой и графиком. Слайды 2,3.
VI. Решение заданий обязательной части.
- Какие способы решения систем уравнений вы знаете? Слайд 4.
Слайд 4. - В чем заключается способ подстановки решения системы двух линейных уравнений с двумя переменными? (каждому ученику распечатать алгоритмы)
-Применяя этот способ, решить систему уравнений: (задание дано на карточках)
 №1. 2х + у = 2
№1. 2х + у = 2
6х – 2у = 1 (решают на доске и в тетрадях)
- В чем заключается способ сложения? Решить систему уравнений способом сложения.
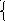 №2. 2х + 2у = 10
№2. 2х + 2у = 10
3х - 4у= 1 (решают на доске и в тетрадях)
- В чем заключается графический способ решения системы уравнений с двумя переменными? Решить графическим способом систему уравнений:
 №3. у – 2х = 5
№3. у – 2х = 5
4х + 2у = 6 (решают на доске и в тетрадях)
Ребята, напоминаю вам, что графический способ решения систем уравнений трудоемок и дает приблизительные ответы, но бывают такие виды систем нелинейных уравнений, которые можно решить только этим способом.
VII. Физкультминутка.
Много ль надо нам, ребята, для умелых наших рук?
Нарисуем два квадрата, а на них огромный круг.
А потом еще кружочек, треугольный колпачок.
Вот и вышел очень, очень развеселый чудачок.
(Дети рисуют в воздухе геометрические фигуры.)
VIII. Решение задач с помощью систем уравнений.
- Где находит применение теория систем уравнений? (при решении задач)
(Повторяется схема решения задач с помощью систем уравнений). Слайд 5.
- Сейчас вы увидите только часть решения некоторой задачи. Попробуйте по этой части сформулировать всю задачу. Слайд 6.
Пусть стороны прямоугольника будут х и у см. Тогда имеем:
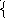 х – у = 4
х – у = 4
2(х + у) = 20 Ученики составляют задачу.
Задача. Периметр прямоугольника равен 20 см., а одна из сторон больше другой на 4 см.. Найдите стороны прямоугольника.
- А теперь откройте учебник на стр. 183, решаем задачу № 10.
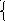 3х + 5у = 50 -6х – 10у = -100
3х + 5у = 50 -6х – 10у = -100
6х + 3у = 51 -7у = -49; у = 7 авторучек; 3х + 35 = 50; х = 5 карандашей.
IX. Тестовые задания.
ТЕСТ по теме «Системы линейных уравнений».
1. Какие из перечисленных уравнений являются линейными?
а) х – 2у = 1; б) ху + 3у = - 18
в) х2 + 2у = 5; г) – х – у = - 11.
2. Какая из перечисленных пар чисел является решением системы уравнений
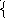 2х + у = 12,
2х + у = 12,
х – 2у = 2?
а) (2; 0); б) (1; -2); в) (4; 4); г) (5,2; 1,6).
3. Какая из перечисленных систем не имеет решения?
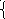
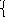
 а) 2х + у = 5 б) 2х + 3у = 8 в) х – у = 6,
а) 2х + у = 5 б) 2х + 3у = 8 в) х – у = 6,
4х +2у = 10 3х – у = - 9 х – у = - 3
4. Какая из перечисленных систем имеет одно решение?
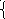
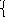
 а) 2х + у = 5 б) 2х + 3у = 8 в) х – у = 6,
а) 2х + у = 5 б) 2х + 3у = 8 в) х – у = 6,
4х +2у = 10 3х – у = - 9 х – у = - 3
5. Какая из перечисленных систем имеет множество решений?
 а) 2х + у = 5 б) 2х + 3у = 8 в) х – у = 6,
а) 2х + у = 5 б) 2х + 3у = 8 в) х – у = 6,
4х +2у = 10 3х – у = - 9 х – у = - 3
Ответы: 1) а; г 2) г 3) в 4) б 5) а
X. Странички истории.
Существует, ребята, еще один способ решения систем уравнений, который мы с вами еще не рассматривали. Это метод - метод перебора или подбора. Например, дается система:
 х + у = 7,
х + у = 7,
х – у = 1
Можно легко подобрать значения х и у: х = 4, у = 3
-Попробуйте решить систему методом подбора:
 х + у = 5
х + у = 5
х2 - у = 7, х = 3, у = 2
Все эти способы решения систем уравнений знали люди давно. Точной даты неизвестно, но они имеются в книге Ньютона «Всеобщая арифметика», которая была издана в 1707 году.
XI. Итоги урока.
- Итак, ребята, мы заканчиваем изучение темы «Системы уравнений».
А сейчас, ответьте, пожалуйста, на такие вопросы:
1.Чему вы учились сегодня на уроке?
2. Какой способ решения систем уравнений с двумя переменными вам понравился больше?
3. Где могут применяться знания о системах уравнений с двумя переменными?
( Математические методы используются при решении задач с практическим содержанием. Это могут быть задачи по физике, химии, расчет биополей по биологии и т.д.)
4. А какие системы окружают нас повседневной жизни? Слайды 7,8,9,10
(ученики вспоминают о предметах, где они встречали системы: русский язык - соединительные союзы, биология -система кровообращения человека, физика - система СИ, химия - периодическая система элементов, астрономия - Солнечная система.)
б) В оценочных листах выставите себе итоговую оценку. Оценки за урок, комментирование.
XII. Домашнее задание. повторять п. 4.1 – п. 4.6, составить математические модели к задачам, одну решить (по выбору). Учащимся карточки.
Домашнее задание.
Задача иранского ученого XVI века Бехаэддина: Разделить число 10 на 2 части, разность которых 5.
Задача Бхаскары: Некто сказал другу: «Дай мне 100 рупий и я буду богаче тебя вдвое». Друг ответил: «Дай мне только 10 и я стану в 6 раз богаче тебя». Сколько рупий было у каждого?
Задача из рассказа А.П.Чехова «Репетитор»: Купец купил 130 аршин черного и синего сукна за 540 рублей. Спрашивается, сколько аршин он купил того и другого, если синее сукно стоило 5 рублей за аршин, а черное 3 рубля?
Задача Ал – Хорезми: Найти два числа, зная, что их сумма равна 10, а отношение 4.
XIII. Рефлексия . Слайд 11.
Прием рефлексии «Мишень». Учащиеся должны поставить точку в каждом секторе.
Учащимся карточки.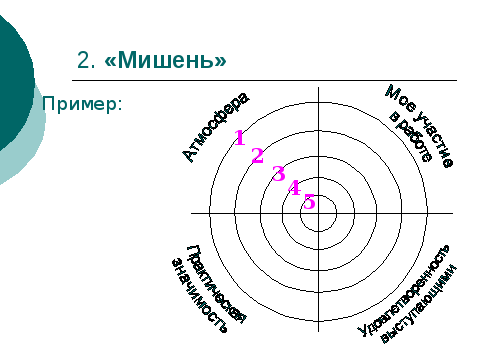
|
| Домашнее задание. | Игра «Крестики - нолики | Устная работа. | Работа у доски. | Решение задач. | Тестовые задания. | Активность на уроке | Итоговая оценка |
| Белоусова В. |
|
|
|
|
|
|
|
|
| Еленский А. |
|
|
|
|
|
|
|
|
| Коновалов А. |
|
|
|
|
|
|
|
|
Ответы к игре
«Крестики – нолики»:
Х 0 Х 0 Х Х 0
Ответы к тесту:
1)а, г; 2)г; 3)в; 4)б; 5)а.
ТЕСТ по теме «Системы линейных уравнений».
1. Какие из перечисленных уравнений являются линейными?
а) х – 2у = 1; б) ху + 3у = - 18
в) х2 + 2у = 5; г) – х – у = - 11.
2. Какая из перечисленных пар чисел является решением системы уравнений
 2х + у = 12,
2х + у = 12,
х – 2у = 2?
а) (2; 0); б) (1; -2); в) (4; 4); г) (5,2; 1,6).
3. Какая из перечисленных систем не имеет решения?
 а) 2х + у = 5 б) 2х + 3у = 8 в) х – у = 6,
а) 2х + у = 5 б) 2х + 3у = 8 в) х – у = 6,
4х +2у = 10 3х – у = - 9 х – у = - 3
4. Какая из перечисленных систем имеет одно решение?
 а) 2х + у = 5 б) 2х + 3у = 8 в) х – у = 6,
а) 2х + у = 5 б) 2х + 3у = 8 в) х – у = 6,
4х +2у = 10 3х – у = - 9 х – у = - 3
5. Какая из перечисленных систем имеет множество решений?
 а) 2х + у = 5 б) 2х + 3у = 8 в) х – у = 6,
а) 2х + у = 5 б) 2х + 3у = 8 в) х – у = 6,
4х +2у = 10 3х – у = - 9 х – у = - 3
---------------------------------------------------------------------------------------------------------------
ТЕСТ по теме «Системы линейных уравнений».
1. Какие из перечисленных уравнений являются линейными?
а) х – 2у = 1; б) ху + 3у = - 18
в) х2 + 2у = 5; г) – х – у = - 11.
2. Какая из перечисленных пар чисел является решением системы уравнений
 2х + у = 12,
2х + у = 12,
х – 2у = 2?
а) (2; 0); б) (1; -2); в) (4; 4); г) (5,2; 1,6).
3. Какая из перечисленных систем не имеет решения?
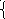
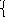
 а) 2х + у = 5 б) 2х + 3у = 8 в) х – у = 6,
а) 2х + у = 5 б) 2х + 3у = 8 в) х – у = 6,
4х +2у = 10 3х – у = - 9 х – у = - 3
4. Какая из перечисленных систем имеет одно решение?
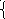
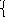
 а) 2х + у = 5 б) 2х + 3у = 8 в) х – у = 6,
а) 2х + у = 5 б) 2х + 3у = 8 в) х – у = 6,
4х +2у = 10 3х – у = - 9 х – у = - 3
5. Какая из перечисленных систем имеет множество решений?
 а) 2х + у = 5 б) 2х + 3у = 8 в) х – у = 6,
а) 2х + у = 5 б) 2х + 3у = 8 в) х – у = 6,
4х +2у = 10 3х – у = - 9 х – у = - 3
---------------------------------------------------------------------------------------------------------------
ТЕСТ по теме «Системы линейных уравнений».
1. Какие из перечисленных уравнений являются линейными?
а) х – 2у = 1; б) ху + 3у = - 18
в) х2 + 2у = 5; г) – х – у = - 11.
2. Какая из перечисленных пар чисел является решением системы уравнений
 2х + у = 12,
2х + у = 12,
х – 2у = 2?
а) (2; 0); б) (1; -2); в) (4; 4); г) (5,2; 1,6).
3. Какая из перечисленных систем не имеет решения?
 а) 2х + у = 5 б) 2х + 3у = 8 в) х – у = 6,
а) 2х + у = 5 б) 2х + 3у = 8 в) х – у = 6,
4х +2у = 10 3х – у = - 9 х – у = - 3
4. Какая из перечисленных систем имеет одно решение?
 а) 2х + у = 5 б) 2х + 3у = 8 в) х – у = 6,
а) 2х + у = 5 б) 2х + 3у = 8 в) х – у = 6,
4х +2у = 10 3х – у = - 9 х – у = - 3
5. Какая из перечисленных систем имеет множество решений?
 а) 2х + у = 5 б) 2х + 3у = 8 в) х – у = 6,
а) 2х + у = 5 б) 2х + 3у = 8 в) х – у = 6,
4х +2у = 10 3х – у = - 9 х – у = - 3
---------------------------------------------------------------------------------------------------------------
Алгоритм решения систем уравнений способом подстановки.
1) Из одного уравнения системы (все равно из какого) нужно выразить одно неизвестное через другое, допустим у через х;
2) полученное выражение подставить в другое уравнение системы - получится одно уравнение с одним неизвестным х;
3) решив это уравнение, найти значение х;
4) подставив найденное значение х в выражение для у, найти значение у.
-------------------------------------------------------------------------------------------------------------------
Алгоритм решения систем уравнений способом подстановки.
1) Из одного уравнения системы (все равно из какого) нужно выразить одно неизвестное через другое, допустим у через х;
2) полученное выражение подставить в другое уравнение системы - получится одно уравнение с одним неизвестным х;
3) решив это уравнение, найти значение х;
4) подставив найденное значение х в выражение для у, найти значение у.
-------------------------------------------------------------------------------------------------------------------Алгоритм решения систем уравнений способом подстановки.
1) Из одного уравнения системы (все равно из какого) нужно выразить одно неизвестное через другое, допустим у через х;
2) полученное выражение подставить в другое уравнение системы - получится одно уравнение с одним неизвестным х;
3) решив это уравнение, найти значение х;
4) подставив найденное значение х в выражение для у, найти значение у.
-------------------------------------------------------------------------------------------------------------------
Алгоритм решения систем уравнений способом сложения.
1) Уравнять модули коэффициентов при одном из неизвестных;
2) складывая или вычитая почленно полученные уравнения, найти одно неизвестное;
3) подставляя найденное значение в одно из уравнений исходной системы, найдем второе неизвестное.
-------------------------------------------------------------------------------------------------------------------
Алгоритм решения систем уравнений способом сложения.
1) Уравнять модули коэффициентов при одном из неизвестных;
2) складывая или вычитая почленно полученные уравнения, найти одно неизвестное;
3) подставляя найденное значение в одно из уравнений исходной системы, найдем второе неизвестное.
-------------------------------------------------------------------------------------------------------------------
Алгоритм решения систем уравнений способом сложения.
1) Уравнять модули коэффициентов при одном из неизвестных;
2) складывая или вычитая почленно полученные уравнения, найти одно неизвестное;
3) подставляя найденное значение в одно из уравнений исходной системы, найдем второе неизвестное.
-------------------------------------------------------------------------------------------------------------------
Алгоритм решения систем уравнений графическим способом.
1) Строится график каждого из уравнений системы (для этого надо выразить у через х);
2) находятся координаты точек пересечения построенных графиков (если они пересекаются);
3) координаты точки пересечения графиков записывают в ответ (они являются решением системы этих уравнений).
Графический способ применяется при решении практических задач для нахождения приближенных решений.
-------------------------------------------------------------------------------------------------------------------
Алгоритм решения систем уравнений графическим способом.
1) Строится график каждого из уравнений системы (для этого надо выразить у через х);
2) находятся координаты точек пересечения построенных графиков (если они пересекаются);
3) координаты точки пересечения графиков записывают в ответ (они являются решением системы этих уравнений).
Графический способ применяется при решении практических задач для нахождения приближенных решений.
-------------------------------------------------------------------------------------------------------------------
Алгоритм решения систем уравнений графическим способом.
1) Строится график каждого из уравнений системы (для этого надо выразить у через х);
2) находятся координаты точек пересечения построенных графиков (если они пересекаются);
3) координаты точки пересечения графиков записывают в ответ (они являются решением системы этих уравнений).
Рефлексия «Мишень».
------------------------------------------------------------------------------------------------------------------------------------
Рефлексия «Мишень».

----------------------------------------------- --------------------------------------------------------------------------------
Оценочный лист ученика(цы) 8 класса_____________________________________________________
по теме «Системы уравнений».
| № | Этапы урока | оценка |
| 1 | Выполнение домашнего задания. |
|
| 2 | Проверка теоретического материала. Игра «Крестики-нолики». |
|
| 3 | Актуализация знаний. Устная работа. |
|
| 4 | Решение систем. Работа у доски. |
|
| 5 | Решение задач с помощью систем уравнений. |
|
| 6 | ТЕСТ по теме «Системы линейных уравнений». |
|
| 7 | Моя активность на уроке. |
|
|
| Итоговая оценка за урок |
|
-------------------------------------------------------------------------------------------------------------------------
Оценочный лист ученика(цы) 8 класса_____________________________________________________
по теме «Системы уравнений».
| № | Этапы урока | оценка |
| 1 | Выполнение домашнего задания. |
|
| 2 | Проверка теоретического материала. Игра «Крестики-нолики». |
|
| 3 | Актуализация знаний. Устная работа. |
|
| 4 | Решение систем. Работа у доски. |
|
| 5 | Решение задач с помощью систем уравнений. |
|
| 6 | ТЕСТ по теме «Системы линейных уравнений». |
|
| 7 | Моя активность на уроке. |
|
|
| Итоговая оценка за урок |
|
-------------------------------------------------------------------------------------------------------------------------
Оценочный лист ученика(цы) 8 класса_____________________________________________________
по теме «Системы уравнений».
| № | Этапы урока | оценка |
| 1 | Выполнение домашнего задания. |
|
| 2 | Проверка теоретического материала. Игра «Крестики-нолики». |
|
| 3 | Актуализация знаний. Устная работа. |
|
| 4 | Решение систем. Работа у доски. |
|
| 5 | Решение задач с помощью систем уравнений. |
|
| 6 | ТЕСТ по теме «Системы линейных уравнений». |
|
| 7 | Моя активность на уроке. |
|
|
| Итоговая оценка за урок |
|
-------------------------------------------------------------------------------------------------------------------------
«Где есть желание – найдется путь!»
-----------------------------------
Домашнее задание.
1. Задача иранского ученого XVI века Бехаэддина: Разделить число 10 на 2 части, разность которых 5.
2. Задача Бхаскары: Некто сказал другу: «Дай мне 100 рупий и я буду богаче тебя вдвое». Друг ответил: «Дай мне только 10 и я стану в 6 раз богаче тебя». Сколько рупий было у каждого?
3. Задача из рассказа А.П.Чехова «Репетитор»: Купец купил 130 аршин черного и синего сукна за 540 рублей. Спрашивается, сколько аршин он купил того и другого, если синее сукно стоило 5 рублей за аршин, а черное 3 рубля?
4. Задача Ал – Хорезми: Найти два числа, зная, что их сумма равна 10, а отношение 4.
--------------------------------------------------------------------------------------
Домашнее задание.
1. Задача иранского ученого XVI века Бехаэддина: Разделить число 10 на 2 части, разность которых 5.
2. Задача Бхаскары: Некто сказал другу: «Дай мне 100 рупий и я буду богаче тебя вдвое». Друг ответил: «Дай мне только 10 и я стану в 6 раз богаче тебя». Сколько рупий было у каждого?
3. Задача из рассказа А.П.Чехова «Репетитор»: Купец купил 130 аршин черного и синего сукна за 540 рублей. Спрашивается, сколько аршин он купил того и другого, если синее сукно стоило 5 рублей за аршин, а черное 3 рубля?
4. Задача Ал – Хорезми: Найти два числа, зная, что их сумма равна 10, а отношение 4.
--------------------------------------------------------------------------------------
Домашнее задание.
1. Задача иранского ученого XVI века Бехаэддина: Разделить число 10 на 2 части, разность которых 5.
2. Задача Бхаскары: Некто сказал другу: «Дай мне 100 рупий и я буду богаче тебя вдвое». Друг ответил: «Дай мне только 10 и я стану в 6 раз богаче тебя». Сколько рупий было у каждого?
3. Задача из рассказа А.П.Чехова «Репетитор»: Купец купил 130 аршин черного и синего сукна за 540 рублей. Спрашивается, сколько аршин он купил того и другого, если синее сукно стоило 5 рублей за аршин, а черное 3 рубля?
4. Задача Ал – Хорезми: Найти два числа, зная, что их сумма равна 10, а отношение 4.
--------------------------------------------------------------------------------------
Домашнее задание.
1. Задача иранского ученого XVI века Бехаэддина: Разделить число 10 на 2 части, разность которых 5.
2. Задача Бхаскары: Некто сказал другу: «Дай мне 100 рупий и я буду богаче тебя вдвое». Друг ответил: «Дай мне только 10 и я стану в 6 раз богаче тебя». Сколько рупий было у каждого?
3. Задача из рассказа А.П.Чехова «Репетитор»: Купец купил 130 аршин черного и синего сукна за 540 рублей. Спрашивается, сколько аршин он купил того и другого, если синее сукно стоило 5 рублей за аршин, а черное 3 рубля?
4. Задача Ал – Хорезми: Найти два числа, зная, что их сумма равна 10, а отношение 4.
--------------------------------------------------------------------------------------





 б) №9. у = 2 + х
б) №9. у = 2 + х
 №1. 2х + у = 2
№1. 2х + у = 2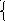 №2. 2х + 2у = 10
№2. 2х + 2у = 10 №3. у – 2х = 5
№3. у – 2х = 5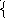 х – у = 4
х – у = 4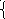
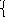
 а) 2х + у = 5 б) 2х + 3у = 8 в) х – у = 6,
а) 2х + у = 5 б) 2х + 3у = 8 в) х – у = 6, х + у = 7,
х + у = 7, х + у = 5
х + у = 5

















