Урок 4/10
подробно презентация
Тема: Обобщение и уточнение Ньютоном законов Кеплера
Ход урока:
Новый материал (30мин)
1. Закон всемирного тяготения.
Сообщение ученика = Книга “Астрономия в ее развитии” = Рождение великого закона (стр. 38).
| Повторение законов Кеплера:
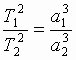 I. Все планеты Солнечной системы вращаются вокруг Солнца по эллиптическим орбитам, в одном из фокусов которых находится Солнце. I. Все планеты Солнечной системы вращаются вокруг Солнца по эллиптическим орбитам, в одном из фокусов которых находится Солнце.
II. Радиус-вектор планеты за одинаковые промежутки времени описывает равные площади: скорость движения планет максимальна в перигелии и минимальна в афелии.
III. Квадраты периодов обращения планет вокруг Солнца соотносятся между собой, как кубы их средних расстояний от Солнца: |
| 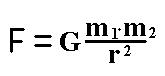 Исаак НЬЮТОН (1643-1727) в 1686г в 3-х книгах "Математические начала натуральной философии", излагает учение о всемирном тяготении и теорию движения небесных тел. Исаак НЬЮТОН (1643-1727) в 1686г в 3-х книгах "Математические начала натуральной философии", излагает учение о всемирном тяготении и теорию движения небесных тел. Сила тяготения между Солнцем и планетой пропорциональна произведению их масс и обратно пропорциональна квадрату расстояния между ними. | Гравитация – общее свойство всех тел природы. Для небесных тел объясняет: |
| Можно показать упрощенный вывод закона Всемирного тяготения описан в учебнике физики для X классов физико-математических школ под редакцией А.А. Пинского. Если планеты движутся по почти круговым орбитам, их центростремительные ускорения равны: 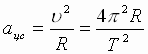 , где Т – период обращения планеты вокруг Солнца, R - радиус орбиты планеты. Из III закона Кеплера , где Т – период обращения планеты вокруг Солнца, R - радиус орбиты планеты. Из III закона Кеплера 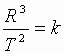 или или 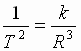 . Следовательно, ускорение любой планеты независимо от ее массы обратно пропорционально квадрату радиуса ее орбиты: . Следовательно, ускорение любой планеты независимо от ее массы обратно пропорционально квадрату радиуса ее орбиты: 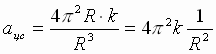 . Согласно II закону Ньютона, сила F, сообщающая планете это ускорение, равна: . Согласно II закону Ньютона, сила F, сообщающая планете это ускорение, равна: 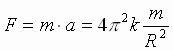 (1) сила, действующая на любую планету, прямо пропорциональна массе планеты и обратно пропорциональна квадрату расстояния от нее до Солнца. (1) сила, действующая на любую планету, прямо пропорциональна массе планеты и обратно пропорциональна квадрату расстояния от нее до Солнца.
Согласно III закону Ньютона, сила F', действующая на планету со стороны Солнца, равна ей по модулю, противоположна по направлению и равна 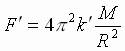 : где М – масса Солнца. : где М – масса Солнца.
Поскольку F = F',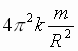 = =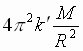 . Обозначим . Обозначим 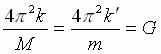 где G – постоянная величина. Тогда где G – постоянная величина. Тогда 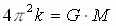 и выражение (1) можно записать в виде известной нам формулы закона Всемирного тяготения: и выражение (1) можно записать в виде известной нам формулы закона Всемирного тяготения: 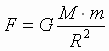 |
| Законы Кеплера как движутся, то ЗВт почему так движутся. 4 закона (3 закона Кеплера и 3Вт) основные законы Небесной механики – раздела астрономии, исследующего движение небесных тел под действием взаимного притяжения. Понятие “небесная механика” ввел в 1799г Пьер Симон Лапласс (1749-1827, Франция) в астрономии исследовал сложные случаи возмущенного движения космических тел (вековые возмущения Юпитера, Сатурна, Луны; фигуры планет; движение полюсов Земли; первая теория движения спутников Юпитера и динамической теории приливов; обоснование механической устойчивости Солнечной системы). Пятитомный "Трактат о небесной механике" стал классическим трудом и в течении 50 лет был основным руководством для астрономов в данном разделе науки. |
2. Возмущения, открытие других планет.
С глубокой древности, видимые невооруженным глазом, людям были известны 5 планет (Какие?). Н. Коперник научно обосновал, что Земля тоже планета СС.
В 1781г Уильям Гершель (1738 – 1822, Англия) 13 марта в 10ч вечера открыл Уран (правда считал, что это комета и лишь через 4 месяца российский астроном А.И. Лексель (1740 –1784) указал, что это планета.
А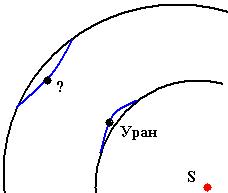 строномы рассчитали орбиту Урана, используя законы небесной механики, но скоро выяснилось, что Уран отклоняется от Кеплеровской (эллиптической) орбиты. Почему?
строномы рассчитали орбиту Урана, используя законы небесной механики, но скоро выяснилось, что Уран отклоняется от Кеплеровской (эллиптической) орбиты. Почему?
1. Действие Сатурна или Юпитера (выяснилось, – нет).
2. За Ураном есть еще планета?
Изменения характеристик движения космических тел вследствие притяжения со стороны других космических тел, помимо центрального, называются возмущениями и наблюдаются в виде отклонений от траекторий, вычисленных на основе задачи 2-х тел (законов Кеплера). Невозмущенным называется довольно редкий вид движения космических тел, строго подчиняющегося законам Кеплера.
Закон всемирного тяготения решает задачу взаимодействия двух тел, а тут задача взаимного притяжения трех тел. В реальных ситуациях космические системы только из 2-х тел встречаются сравнительно редко. Чаще приходится описывать движение 3-х небесных тел, определяя движение 2-х тел относительно третьего или всех трех тел относительно центра масс (например, для системы Земля - Луна - Солнце). Точное решение задачи 3-х тел (Зундман, 1912г) носит очень сложный характер и, как правило, заменяется приближенным решением.
Джон Адамс (1819-1892, Англия) – студент, начав с 1844г расчеты, к сентябрю 1845г указал, где искать новую планету. Но ни профессор Кембриджского университета Уэллис, ни директор Гринвичской обсерватории Джорж Эри (1801-1892) не предприняли ее поиска –проигнорировали расчеты молодого математика.
Во Франции Урбен Леверье (1811-1877) так же решил сверхсложную задачу в 1846г используя теорию возмущений, опубликовал три статьи и 18 сентября отправил письмо астроному Берлинской обсерватории Иогану Галле (1812-1910), который 23 сентября 1846г в 52' от указанного места открыл 8-ю планету – Нептун. Кстати, в конце 1612 – начале 1613г в журнале наблюдений Г.Галилея есть зарисованная звездочка- это был Нептун, но ни он, ни Лаланд, наблюдавший Нептун 8 и10 мая 1795г, не обратили внимания.
13 марта 1930г Клайд Томбо (1906-1997, США) сообщает об открытии девятой планеты - Плутона (исключен 24.08.2006г из числа больших планет). Орбита была рассчитана еще в 1905г американскими астрономами Персиваль Ловелл (на фото у него был Плутон, но он не обратил на это внимания) и Эдуардом Пикеринг (1846- 1919) подтверждена в 1915г.
Расчеты, позволившие открыть 8-ю и 9-ю планеты (а так же ряд астероидов) доказали справедливость закона всемирного тяготения. 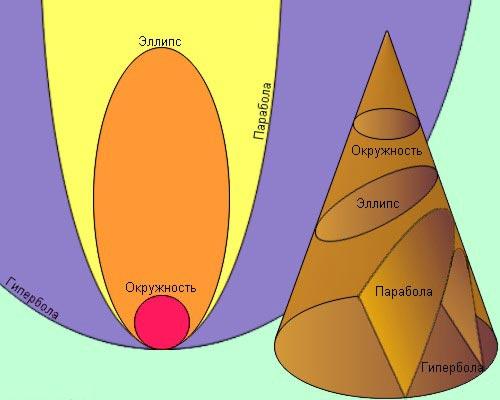
3. Законы Кеплера в формулировки Ньютона.
Сформулировав задачу двух тел (m1, m2 со скоростями v1, v2) и решая ее с помощью высшей математики (находя коэффициенты тел под действием силы взаимного притяжения) Ньютон вывел все законы Кеплера из Закона Всемирного тяготения, при этом открыл и разработал дифференциальное и интегральное исчисление. Спутниками космических объектов называются объекты, вращающиеся вокруг них (общего центра тяжести) под действием сил тяготения. Луна - единственный естественный спутник Земли, а искусственных спутников Земли (ИСЗ) в настоящее время насчитывается свыше 7500. Спутники есть у всех планет Солнечной системы, кроме Меркурия и Венеры. У больших астероидов тоже есть спутники - астероиды поменьше. Все планеты Солнечной системы можно считать спутниками Солнца. Наша Галактика имеет 2 больших спутника - галактики Большое и Малое Магелланово Облако и более 30 других звездных систем поменьше.
I-й закон Кеплера
- формулировка;
- понятие эллипса и формы эллипса;
- ближайшая и наиболее удаленная точка орбиты;
- астрономическая единица.
Допуская неподвижность одного тела, Ньютон доказывает: Под действием силы тяготения одно небесное тело по отношению к другому может двигаться по окружности, эллипсу, параболе и гиперболе (виды канонического сечения). (гравитационные сферы планет).
Первому закону подчиняется и форма орбиты искусственных небесных тел, которая зависит от модуля и направления начальной скорости.
Зависимость формы орбиты от скорости: 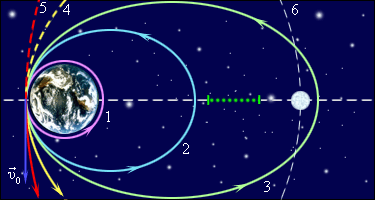
1. Круговая – υo=7,91 км/с. 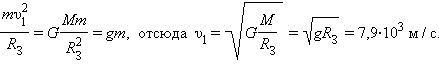 Для ИСЗ, запускаемых на околоземные низкие орбиты (h = 200 км), υI =7,78 км/с. В общем виде первую космическую скорость можем найти по формуле
Для ИСЗ, запускаемых на околоземные низкие орбиты (h = 200 км), υI =7,78 км/с. В общем виде первую космическую скорость можем найти по формуле 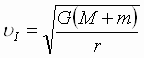
2. Эллиптическая (разной степени вытянутости орбиты): 2 - υ=9 км/с, 3 - υ = 11,1 км/с (облет Луны - сильно вытянутый эллипс).
3. Параболическая 4 - υ2= υo.√2 =11,19 км/с (тело становится ИС Солнца) 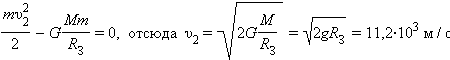 В общем виде вторую космическую скорость можно найти по формуле
В общем виде вторую космическую скорость можно найти по формуле 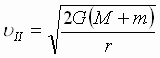
4. Гиперболическая 5 – υ3= υ2.√2 =16,67 км/с (при скорости υ3 12 км/с полет к ближайшим планетам, а при скорости υ316,7 км/с полет к дальним планетам СС.
Скорость, с которой запущенный с Земли КЛА покинет пределы Солнечной системы, называют иногда третьей космической скоростью. Она равна сумме скоростей движения Земли вокруг Солнца и II космической скорости КЛА относительно Земли, υIII = 42 км/с.
Для формирование знаний об истории космонавтики лучше использовать внеклассное занятие, или отдельный урок с выступлениями учащихся по предложенной тематике. Часть материала по истории космонавтики здесь.
2-й закон Кеплера
1) формулировка;
2) изменение скорости и энергии.
Закон не потребовал уточнения.
3-й закон Кеплера
- формулировка;
- комментарий формулы.
| И. Ньютон решая задачу двух тел, вращающихся вокруг общего центра, найдя их получаемые ускорения из закона всемирного тяготения и через угловую скорость центростремительное ускорение получил уточненный 3-й закон Кеплера с массами тел. Вывод может выглядеть так: |
| Угловая скорость их обращения вокруг центра масс равна 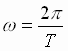 , где Т – период обращения. Тогда центростремительное ускорение тел: , где Т – период обращения. Тогда центростремительное ускорение тел: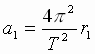 , ,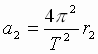 (2), где r1 и r2 - расстояния тел от центра масс системы. Приравнивая выражения (1) и (2), получим: (2), где r1 и r2 - расстояния тел от центра масс системы. Приравнивая выражения (1) и (2), получим: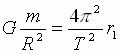 , , 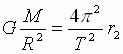 (3). Складывая почленно выражения (3), получим: (3). Складывая почленно выражения (3), получим: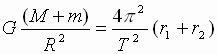 → → 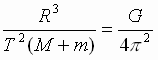 (4). В правой части выражения (4) находятся лишь постоянные величины, откуда следует его справедливость для любой системы двух гравитационно взаимодействующих тел. Для двух космических систем это выражение запишется в виде уточненного III закона Кеплера: (4). В правой части выражения (4) находятся лишь постоянные величины, откуда следует его справедливость для любой системы двух гравитационно взаимодействующих тел. Для двух космических систем это выражение запишется в виде уточненного III закона Кеплера: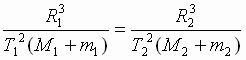 → →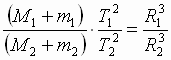 |
| 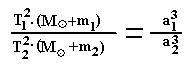 (17) (17)
| Квадраты сидерических периодов планет, умноженные на сумму масс Солнца и соответствующей планеты, относятся как кубы больших полуосей орбит планет. Закон применим не только для планет, но и спутников и позволяет определить массу любого тела в связанной системе движущихся тел. (запомнить, что в сумме масс всегда ставится объект и его спутник). |
II. Закрепление материала (8 мин)
Просмотреть пример №5 (стр. 46).
Решается задача №8 (стр. 47).
Решается задача №7 (стр. 47).
Индивидуальные карточки по теме "Законы Кеплера" (Н.Н. Гомулина)
CD- "Red Shift 5.1" Планеты СС- их нахождение в данный момент времени: созвездия, координаты, угловое удаление от Солнца, Луны.
Итог:
1) Закон всемирного тяготения?
2) В чем заключалось уточнение Ньютоном 1-го закона Кеплера?
3) В чем заключалось уточнение Ньютоном 3-го закона Кеплера?
4) Оценки
Домашнее задание: §10, вопросы стр.47, СР№5 стр. 52 п.6-9.
Задачи:
1. Деймос, один из спутников Марса, отстоит от планеты на расстоянии 23500 км и совершает один оборот вокруг Марса за 30 часов 18 минут. Зная среднее расстояние Земли от Солнца и сидерический период Земли, вычислите отношение масс Марса и Солнца.
2. Какую скорость должна иметь на старте с поверхности Луны (Марса) ракета, доставляющая на Землю образцы грунта?







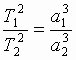 I. Все планеты Солнечной системы вращаются вокруг Солнца по эллиптическим орбитам, в одном из фокусов которых находится Солнце.
I. Все планеты Солнечной системы вращаются вокруг Солнца по эллиптическим орбитам, в одном из фокусов которых находится Солнце.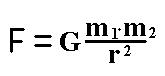 Исаак НЬЮТОН (1643-1727) в 1686г в 3-х книгах "Математические начала натуральной философии", излагает учение о всемирном тяготении и теорию движения небесных тел.
Исаак НЬЮТОН (1643-1727) в 1686г в 3-х книгах "Математические начала натуральной философии", излагает учение о всемирном тяготении и теорию движения небесных тел. 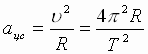 , где Т – период обращения планеты вокруг Солнца, R - радиус орбиты планеты. Из III закона Кеплера
, где Т – период обращения планеты вокруг Солнца, R - радиус орбиты планеты. Из III закона Кеплера 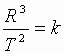 или
или 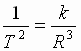 . Следовательно, ускорение любой планеты независимо от ее массы обратно пропорционально квадрату радиуса ее орбиты:
. Следовательно, ускорение любой планеты независимо от ее массы обратно пропорционально квадрату радиуса ее орбиты: 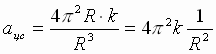 . Согласно II закону Ньютона, сила F, сообщающая планете это ускорение, равна:
. Согласно II закону Ньютона, сила F, сообщающая планете это ускорение, равна: 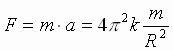 (1) сила, действующая на любую планету, прямо пропорциональна массе планеты и обратно пропорциональна квадрату расстояния от нее до Солнца.
(1) сила, действующая на любую планету, прямо пропорциональна массе планеты и обратно пропорциональна квадрату расстояния от нее до Солнца.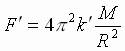 : где М – масса Солнца.
: где М – масса Солнца.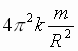 =
=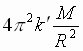 . Обозначим
. Обозначим 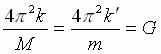 где G – постоянная величина. Тогда
где G – постоянная величина. Тогда 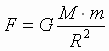
 строномы рассчитали орбиту Урана, используя законы небесной механики, но скоро выяснилось, что Уран отклоняется от Кеплеровской (эллиптической) орбиты. Почему?
строномы рассчитали орбиту Урана, используя законы небесной механики, но скоро выяснилось, что Уран отклоняется от Кеплеровской (эллиптической) орбиты. Почему?

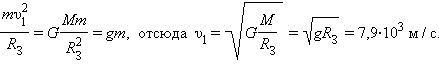 Для ИСЗ, запускаемых на околоземные низкие орбиты (h = 200 км), υI =7,78 км/с. В общем виде первую космическую скорость можем найти по формуле
Для ИСЗ, запускаемых на околоземные низкие орбиты (h = 200 км), υI =7,78 км/с. В общем виде первую космическую скорость можем найти по формуле 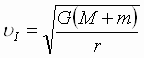
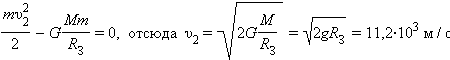 В общем виде вторую космическую скорость можно найти по формуле
В общем виде вторую космическую скорость можно найти по формуле 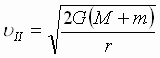
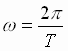 , где Т – период обращения. Тогда центростремительное ускорение тел:
, где Т – период обращения. Тогда центростремительное ускорение тел: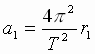 ,
,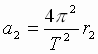 (2), где r1 и r2 - расстояния тел от центра масс системы. Приравнивая выражения (1) и (2), получим:
(2), где r1 и r2 - расстояния тел от центра масс системы. Приравнивая выражения (1) и (2), получим: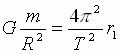 ,
, 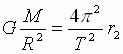 (3). Складывая почленно выражения (3), получим:
(3). Складывая почленно выражения (3), получим: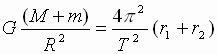 →
→ 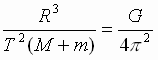 (4). В правой части выражения (4) находятся лишь постоянные величины, откуда следует его справедливость для любой системы двух гравитационно взаимодействующих тел. Для двух космических систем это выражение запишется в виде уточненного III закона Кеплера:
(4). В правой части выражения (4) находятся лишь постоянные величины, откуда следует его справедливость для любой системы двух гравитационно взаимодействующих тел. Для двух космических систем это выражение запишется в виде уточненного III закона Кеплера: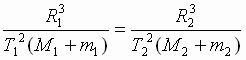 →
→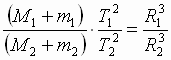
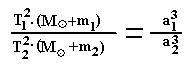 (17)
(17)









