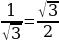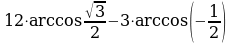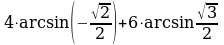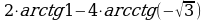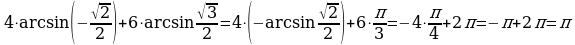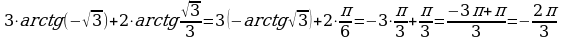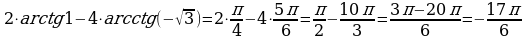Тема занятия: Обратные тригонометрические функции
План:
-
Понятие обратных тригонометрических функций
-
Вычисление обратных тригонометрических функций по таблице
-
Упражнения с решениями
-
Самостоятельная работа
Понятие обратных тригонометрических функций
Мы знаем, что синус, косинус, тангенс и котангенс работают с углами. Но существуют такие задачи, в которых угол не известен, а известно значение самой тригонометрической функции. Как же определить угол?
Для решения таких задач изучают обратные тригонометрические функции. К ним относят арксинус, арккосинус, арктангенс, арккотангенс. Разберемся в их определениях.
-
Арксинус
Определение. Арксинусом числа b называется такой угол из отрезка  , синус которого равен b. То есть
, синус которого равен b. То есть
Пример 1. 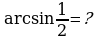
Так как по таблице 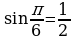 и
и  , то
, то 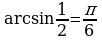
2. Арккосинус
Определение. Арккосинусом числа b называется такой угол из отрезка  , косинус которого равен b. То есть
, косинус которого равен b. То есть
Пример 2. 
Так как по таблице  и
и 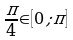 , то
, то 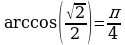
3. Арктангенс
Определение. Арктангенсом числа b называется такой угол из интервала  , тангенс которого равен b. То есть
, тангенс которого равен b. То есть
Пример 3. 
Так как по таблице 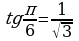 и
и  , то
, то 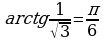 .
.
4. Арккотангенс
Определение. Арккотангенсом числа b называется такой угол из интервала 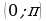 , котангенс которого равен b. То есть
, котангенс которого равен b. То есть
Пример 4. 
Так как по таблице  и
и 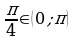 , то
, то 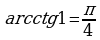 .
.
Вычисление обратных тригонометрических функций по таблице
Все обратные тригонометрические функции можно вычислить по таблице. Например, 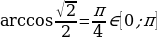 . Ищем в строчке косинуса значение
. Ищем в строчке косинуса значение 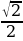 , а затем смотрим наверх, на угол, которому соответствует это значение. Но нужно знать еще правила, по которым вычисляются одинаково по парам: арксинус с арктангенсом; арккосинус с арккотангенсом.
, а затем смотрим наверх, на угол, которому соответствует это значение. Но нужно знать еще правила, по которым вычисляются одинаково по парам: арксинус с арктангенсом; арккосинус с арккотангенсом.

Правило1. Арксинус и арктангенс вычисляются по таблице ТОЛЬКО ИЗ ПЕРВОЙ ЧЕТВЕРТИ. При этом, если число отрицательное, то минус выносится вперед, а затем значения берутся из 1 четверти.
Рассмотрим примеры (проверяйте по таблице)
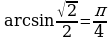



Правило2. Арккосинус и арккотангенс вычисляются по таблице из первой и второй четвертях. При этом, положительное значение берется из 1 четверти, а отрицательное из 2 четверти.
Рассмотрим примеры (проверяйте по таблице)
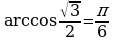
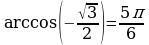
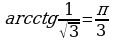
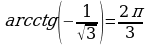
Помним, что 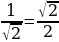 и
и 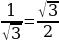
Упражнения с решениями
Пример 5. Вычислите:
а) 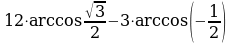
б) 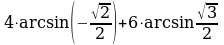
в) 
г) 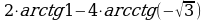
Решение: используя таблицу значений и правила вычисления 1 и 2, получим
а) 
б) 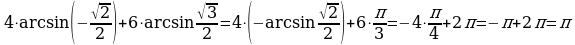
в) 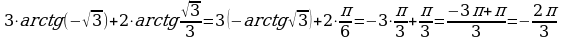
г) 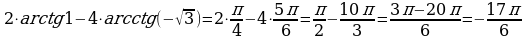







 , синус которого равен b. То есть
, синус которого равен b. То есть
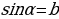
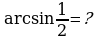
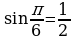 и
и  , то
, то 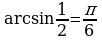
 , косинус которого равен b. То есть
, косинус которого равен b. То есть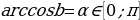
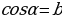

 и
и 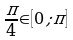 , то
, то 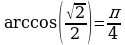
 , тангенс которого равен b. То есть
, тангенс которого равен b. То есть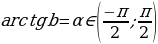
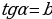

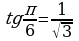 и
и  , то
, то 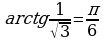 .
.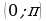 , котангенс которого равен b. То есть
, котангенс которого равен b. То есть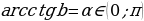
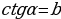

 и
и 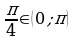 , то
, то 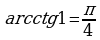 .
.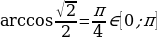 . Ищем в строчке косинуса значение
. Ищем в строчке косинуса значение 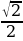 , а затем смотрим наверх, на угол, которому соответствует это значение. Но нужно знать еще правила, по которым вычисляются одинаково по парам: арксинус с арктангенсом; арккосинус с арккотангенсом.
, а затем смотрим наверх, на угол, которому соответствует это значение. Но нужно знать еще правила, по которым вычисляются одинаково по парам: арксинус с арктангенсом; арккосинус с арккотангенсом.
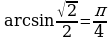



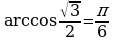
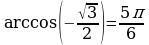
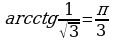
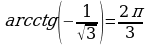
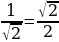 и
и