Образовательный минимум по математике 6 кл за I четверть с примерами в табличной форме.

Наименование темы

Правила

Примеры

Делители и кратные.

Делителем натурального числа n называют число,   на которое n делится без остатка.  

Делителем числа   9   является число   3 ,             9 : 3 = 3 

Oдин (1) — это делитель любого натурального числа.

2 : 1 = 2 ;         4 : 1 = 4 ;       11 : 1 = 11   и. т. д.    

Если число b делитель числа a , то a называют кратным числу b .     a : b = n . 

12 : 6 = 2 ;          двенадцать кратно шести     или  двенадцать  -  кратное числа шесть.    

Признаки делимости

на 10,

на 5,

на 2

Натуральное число делится на 10 без остатка только в том случае,  если оно оканчивается на нуль. 

Если последняя цифра

 натурального числа не 0, то число на 10 без остатка не делится.  

Числа 10, 20, 30 … , 220, 1200, 1210 … и т. д. делятся на 10 без остатка

Натуральное число делится на 5 без остатка в том случае, если оно оканчивается на 0 или на 5

Числа 5, 10, 15, 20 … , 220, 225, … и т. д. делятся на 5 без остатка.

Если последняя цифра в записи натурального числа четная (2, 4, 6, 8) или 0 , то это число делится на 2 без остатка.

Числа   2, 4, 6, 8, 10 … , 220, 222, 224, 226, 228, … , 1200, 1202, 1204, 1206, 1208, 1210, 1212, 1214 … и т. д. делятся на 2 без остатка.  

Признаки делимости

на 9,

на 3

 Натуральное число делится на 3 без остатка, если сумма его цифр    кратна трем.  

Число 762 делится на 3 без остатка, так как сумма его цифр:  

7 + 6 + 2 = 15 — кратна 3       ( 15 : 3=5 ). 

Натуральное число делится на 9 без остатка, если сумма его цифр кратна девяти.

Число 765 делится на 9 без остатка, так как сумма его цифр:

7 + 6 + 5 = 18 — кратна 9 ( 18 : 9=2 ).

Простые и составные числа

Натуральное число называют простым, если оно имеет

только два делителя: единицу и само это число.

 3   делится без остатка на 1 и на 3;  
5   делится без остатка на 1 и на 5;

7 делится без остатка на 1 и на 7; 

Натуральное число называют составным, если оно имеет

более двух делителей.

4 делится без остатка на 1, на 2 и на 4;

8 делится без остатка на 1, на 2, на 4 и на 8;

9   делится без остатка на 1, на 3 и на 9; 

Число 1 имеет только один делитель: само это число (1) .  Поэтому его не относят ни к составным, ни к простым числам.    

 Любое составное число можно разложить на два множителя,  каждый из которых больше 1. Простое число так разложить на   множители нельзя.    

4=2•2 ; 6=2•3 ; 9=3•3 ; 15=3•5 ;

Разложение на простые множители

Всякое составное число можно разложить на простые множители.

1. Проверяем, не является ли предложенное число простым.

2. Если нет, то подбираем, руководствуясь признаками деления делитель, из простых чисел начиная с наименьшего (2, 3, 5 …).

3. Повторяем это действие до тех пор, пока частное не окажется простым числом.

1421=7*7*29 8=2*2*2

Наибольший общий делитель. Взаимно простые числа

Наибольший общий делитель (НОД) двух и более чисел — это самое большее натуральное число, на которое эти числа делятся

без остатка.

НОД(12; 8) = 4,  

            НОД (20;35,50)= 5  

 Если у нескольких чисел нет общих делителей кроме единицы, то эти  числа называются взаимно простыми.  

НОД(5;8)=1 , 

НОД(11;18)=1 , 

  НОД(16; 27)=1

Чтобы найти наибольший общий делитель нескольких натуральных чисел, надо:

1) разложить их на простые множители;

2) из множителей, входящих в разложение одного из этих чисел, вычеркнуть те, которые не входят в разложение других чисел;

3) найти произведение оставшихся множителей.

Найдем НОД (48;36).

1. Разложим числа 48 и 36 на простые множители.

48 = 2 · 2 · 2 · 2 · 3

36 = 2 · 2 · 3 · 3

2. Из множителей, входящих в разложение числа 48 вычеркнем те, которые не входят в разложение числа 36.

48 = 2 · 2 · 2 · 2 · 3

Остаются множители 2, 2 и 3.

3. Перемножим оставшиеся множители и получим 12. Это число и является наибольшим общим делителем чисел 48 и 36.

НОД (48;36) = 2 · 2 · 3 = 12.

Наименьшее общее кратное.

Наименьшим общим кратным натуральных чисел a и b называют наименьшее натуральное число, которое кратно a и b .

НОК (8,6)=24,

НОК (25,50)=100

Чтобы найти наименьшее общее кратное нескольких натуральных чисел, надо:

1) разложить их на простые множители;

2) выписать множители, входящие в разложение одного из чисел;

3) добавить к ним недостающие множители из разложений остальных чисел;

4) найти произведение получившихся множителей.

Найдем НОК (75;60).

1. Разложим числа 75 и 60 на простые множители.

75 = 3 · 5 · 5 60 = 2 · 2 · 3 · 3

2. Выпишем множители, входящие в разложение числа 75: 3, 5, 5.

НОК (75;60) = 3 · 5 · 5 · …

3. Добавим к ним недостающие множители из разложения числа 60, т.е. 2, 2.

НОК (75;60) = 3 · 5 · 5 · 2 · 2

4. Найдем произведение получившихся множителей: НОК (75;60) = 3 · 5 · 5 · 2 · 2 = 300.

Основное свойство дроби.

Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится равная ей дробь.

Две равные дроби являются различными записями одного и того же числа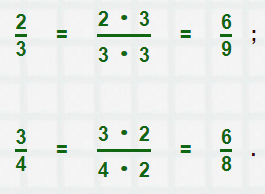

Сокращение дробей

Деление числителя и знаменателя на их общий делитель, отличный от единицы, называют сокращением дроби.

Приведение дробей к общему знаменателю

При приведении дроби к новому знаменателю ее числитель и

знаменатель умножают на дополнительный множитель

Чтобы привести дроби к наименьшему общему знаменателю, надо:

1) найти наименьшее общее кратное знаменателей этих дробей, оно и будет их наименьшим общим знаменателем;

2) разделить наименьший общий знаменатель на знаменатели данных дробей, т. е. найти для каждой дроби дополнительный множитель;

3) умножить числитель и знаменатель каждой дроби на ее дополнительный множитель;

Сравнение, сложение и вычитание дробей с разными знаменателями

Чтобы сравнить (сложить или вычесть) дроби с разными знаменателями, надо:

1) привести данные дроби к наименьшему общему знаменателю;

2) сравнить (сложить или вычесть) полученные дроби.

Сложение и вычитание смешанных чисел

Чтобы сложить смешанные числа:

1) привести дробные части этих чисел к наименьшему общему знаменателю:

2) отдельно выполнить сложение целых частей и отдельно дробных частей. Если при сложении дробных частей получилась неправильная дробь, выделить целую часть из этой дроби и прибавить ее к полученной целой части.

Чтобы выполнить вычитание смешанных чисел, надо:

1) привести дробные части этих чисел к наименьшему общему

знаменателю; если дробная часть уменьшаемого меньше дробной части вычитаемого, превратить ее в неправильную дробь, уменьшив на единицу, целую часть:

2) отдельно выполнить вычитание целых частей и

отдельно дробных частей: