Ոչ ստանդարտ խնդիրների դերը հանրակրթական դպրոցներում: 3-4 դասարաններում
Հայտնի է, որ տեքստային խնդիրների լուծումը մեծ դժվարություն է առաջացնում սովորողների համար: Ամենադժվարը առաջին փուլն է`երբ պետք է վերլուծության ենթարկել խնդրի տեքստը: Աշակերտները դժվար են կողմնորոշվում խնդրի տեքստում, նրա պայմանին և պահանջին:
Խնդրի տեքստը` դա կյանքից վերցրած փաստեր են`
«Մաշան վազեց 100 մետր, իսկ նրան ընդառաջ…»
«Առաջին դասարանի աշակերտները գնեցին 12հատ մեխակ, իսկ երկրորդ դասարանցիները…»
Տեքստում կարևոր է ամեն ինչ, և գործող դեմքերը, և նրանց գործողությունները, և թվային արժեքները: Մենք հենց այդ էլ սովորեցնում ենք, որպեսզի նրանք կարողանան կողմնորոշվել որոշ հատկություններում և օգտագործեն այլ տարբերակներ:
Մաթեմատիկական խնդրի տեքստում ընկած է կենտրոնացման կարողությունը, որը կարևորագույն արդյունք և պայման է աշակերտի ընդհանուր զարգացման մեջ: Կենտրոնացման կարողության զարգացմամբ պետք է զբաղվել ոչ միայն մաթեմատիկայի դասին, այլ նաև ընթերցանության, տեխնոլոգիայի, ֆիզկուլտուրայի և բոլոր դասաժամերի ընթացքում: Երեխայի մտավոր զարգացման մեջ կարևոր է ամեն ինչ, սկսված մանրուքից մինչև բարձրագույն գիտելիքները: Պետք է ստեղծել միջառարկայական կապ ցանկացած առարկայի հետ:
Խնդիր.- Տանձը թանկ է խնձորից 2 անգամ: Ո՞րն է թանկ` 4կգ խնձորը, թե՞ 2կգ տանձը: Կառուցել մոդելը (գրաֆիկը):
Խնձորի գինը /----/
Տանձի գինը /----/----/
4կգ խնձորի գինը /----/----/----/----/
2կգ տանձի գինը /----/----/----/----/
Պատ.` 4կգ խնձորի և 2կգ տանձի արժեքները նույնն են:
Խնդիր.-
Խնդիր.-
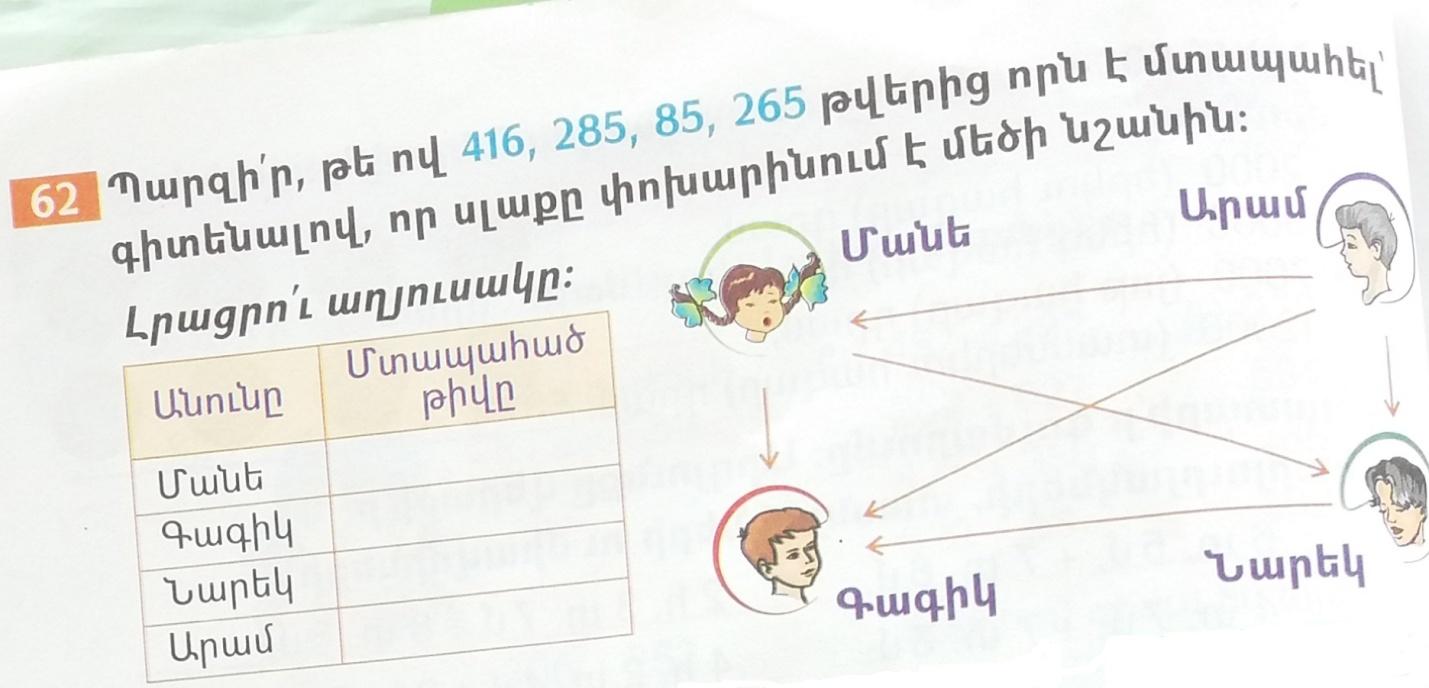
Լուծում.-Ըստ գծագրի Արամի մտապահած թիվը ամենամեծն է 416, Գագիկը` 85,285-ը մտապահել է Մանեն, Նարեկը` 265,:
Խնդիր.- Բանկան մեղրի հետ կշռում է 500գ: Նույն բանկան կերոսինի հետ կշռում է 350գ: Կերոսինը մեղրից թեթև է 2 անգամ: Որքա՞ն է կշռում դատարկ բանկան:
Լուծում.- Գծում ենք գծագիր: Ուշադրություն ենք դարձնում դատարկ բանկայի կշռին և թե ինչպես են կապված մեղրի կշիռն ու կերոսինի կշիռը նույն բանկայի հետ:


Բանկա մեղր 500գ
2 անգամ 350գ
Բանկա կերոսին
Մեղր-2 անգամ ծանր
Կերոսին














Գծագրից պարզ է, որ բանկաների քաշը հավասար է, ըստ պայմանի` մեղրը 2 անգամ ծանր է կերոսինից, ապա 500-350 և կիմանանք, թե ինչքան է նրանց տարբերությունը: Քանի որ բանկաները հավասար են, ապա 150*2=300գ` դա մեղրի իրական քաշն է, իսկ կերոսինինն` 150գ է: Այստեղից էլ հետևում է, որ բանկայի քաշը 200գ է:
500-350=150գ /կերոսին/
150*2=300գ /մեղր /
500+350-(300+150)=400գ / զույգ բանկաները/
400/2=200գ /բանկա/
Պատ`. 200գ
Ընդհանրապես, ոչ ստանդարտ խնդիրները կարելի է դասակարգել ըստ մտածողության, ուշադրության, հիշողության և տրամաբանության զարգացման:
Խնդիր .- Կռահի ́ր օրինաչափությունը և լրացրու ́ դատարկ վանդակները. [ 8 ]

Խնդիր.- [ 8 ]
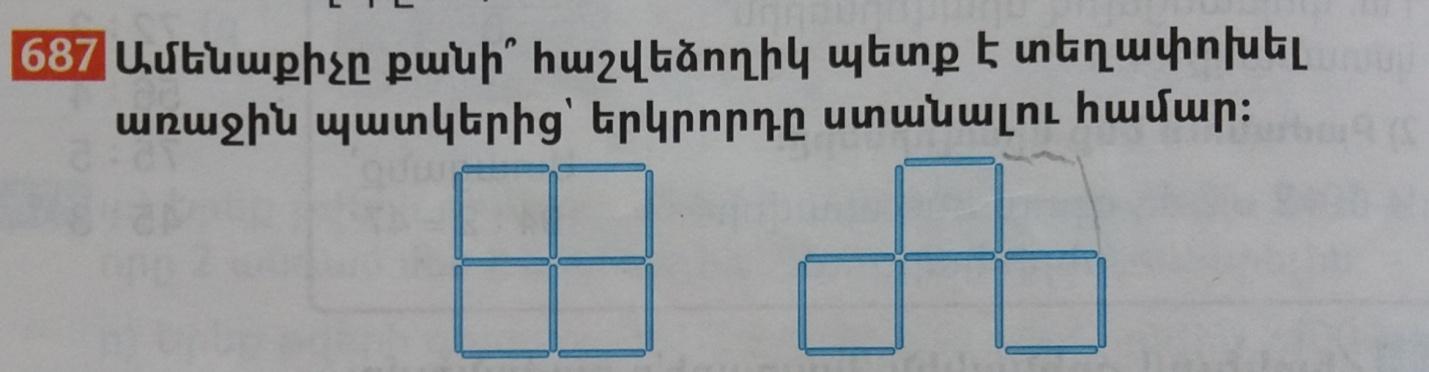
Խնդիր.- [ 9 ]
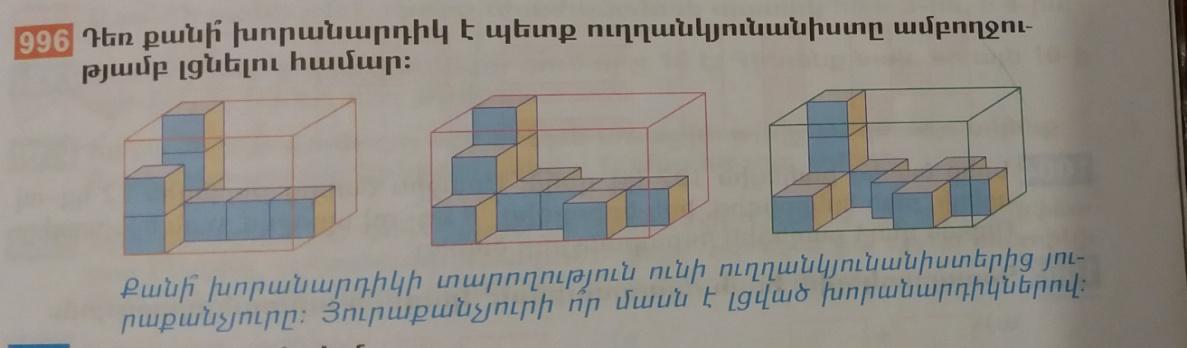
Այս տիպի խնդիրները երեխաները հեշտութամբ են կարողանում լուծել, քանի որ այն տեսողական է և հաշվելով շարքերը, այն կարողանում են վերականգնել:
Խնդիր.- Աշակերտների հիշողությունը մարզելու համար ավելի օգտակար են հետևյալ առաջադրանքները, որոնց հետ աշակերտները սիրով և հետաքրքրությամբ են աշխատում.
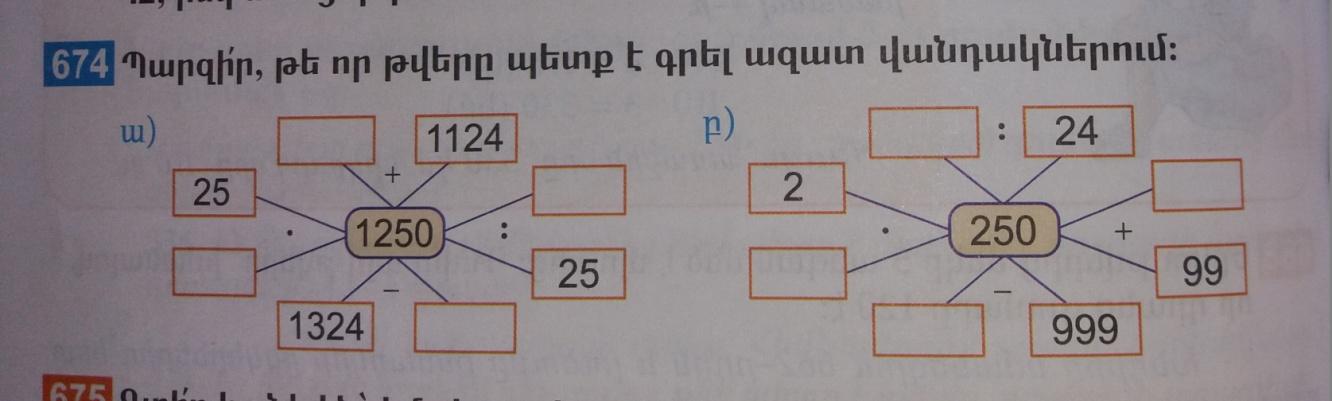 [ 8 ]
[ 8 ]
Այս վարժությունը լուծելու համար պետք է կատարել հակառակ գործողություն, այսինքն 1250 բաժանենք 25 ր ստանանք 25-ի վրա բազմապատկվող թիվը, միայն բաժանման դեպքում չի կատարվի հակառակ գործողություն:
Խնդիր.- 6 թխվածքաբլիթ բաժանեցին եղբայրների և քույրերի միջև այնպես, որ եղբայրների մոտ 2-ով ավելի քիչ է քան քույրերի մոտ: Որքա՞ն թխվածքաբլիթ ստացան եղբայրները և որքա՞ն քույրերը:
 Այս խնդիրը հեշտ է լուծել գծագրի միջոցով:
Այս խնդիրը հեշտ է լուծել գծագրի միջոցով:


6
Ե.

 Ք.
Ք.
Ինչպե՞ս իմանանք, թե քանի վանդակ կա ամեն հատվածում: Քանակը երկու հատվածների հավասար է 6-ի, այսինքն 2 հատվածների քանակը հավասար է քչին: Հավասար է 6-2=4, իսկ նրանցից յուրաքանչյուրը հավասար է 2-ին: Երբ աշակերտներին այս մեկնաբանությունը պարզ լինի, պետք է գրեն հարցերով և գործողություններով: Պետք է հուշել առաջին հարցը.
Որքա՞ն կլինի թխվածքաբլիթ, եթե քույրերի մոտ լինի աւյյնքան, որքան եղբայրների` 6-2=4
Որքա՞ն կար թխվածքաբլիթ եղբայրների մոտ` 4-2=2
Որքա՞ն կար թխվածքաբլիթ քույրերի մոտ` 2+2=4 կամ 6-2=4
Պատ.` եղբայրների մոտ 2, քույրերի`4 :
Խնդիր.- Հորինի հնարավոր շարունակություն տրված թվերի հերթականությանը.
1,1,2,3,5,…,…,…
1+1=2
1+2=3
2+3=5
3+5=8
5+8=13
8+13=21
Առաջին կարևորագույն պայմանն է, որով կարող ենք կառուցել այս հերթականությունը, այսպիսին է` առաջի 2 թվերը գումարելիներ են, իսկ ամեն երրորդը գումարն է, որը նախորդի գումարն է, իսկ հաջորդի գումարելին:
Պատ.` հնարավոր է այսպիսի հերթականություն` 8,13,21:
Խնդիր.- [ 9 ]
Լուծում.-
853-ի լուծում.- Յուրաքանչյուրին հասավ մեկական խնձոր, որովհետև նրանք երեքն էին` հայր, որդի և թոռնիկ / 2 հայր և 2 որդի/:
Խնդիր.- Կոլյան և Վասյան միասին ունեն 15 դրոշմանիշ: Կոլյան դրանցից 2-ը նվիրեց Վասյային: Որքա՞ն դրոշմանիշ եղավ նրանց մոտ միասին:
Պատ.` այս խնդիրը կատակ է, քանի որ նրանց մոտ քանակը չի փոխվի:
Խնդիր.- Թվաբանական գործողությունների և փակագծերի օգնությոմբ (ուղղահայաց, հորիզոնական կամ էլ թեք) ստացեք ճշմարիտ հավասարություն: Օրինակ` 63=7×9, 9x(3+6)=81
Գտեք առնվազն 6 հավասարություններ:
| 15
| 5 | 10 | 42 | 14 | 66 |
| 7
| 6 | 9 | 3 | 56 | 38 |
| 3
| 7 | 42 | 10 | 18 | 28 |
| 63
| 5 | 49 | 2 | 31 | 20 |
| 7
| 13 | 12 | 32 | 43 | 4 |
| 1
| 9 | 3 | 6 | 81 | 5 |
Խնդիր.- Աննայի ակվարիումի բարձրությունը 52 սմ է, իսկ Աննան բոյը 2,5 անգամ մեծ է ակվարիումի բարձրությունից։ Քանի՞ սանտիմետր է Աննայի բոյը։
52*2= 104
52:2=26
104+26=130
Խնդիր.- Ո՞ր պատկերի մակերեսն է 20 միավոր։ Մեկ փոքր քառակուսու մակերեսը համարիր մեկ միավոր։
Պատ.` Դ:
Խնդիր.- Որդու և հոր տարիքը միասին 40 է: Որքա՞ն կլինի նրանց տարիքը միասին 3 տարի հետո:



40





46


Այս խնդրից հայտնի չէ, թե նրանցից յուրաքանչյուրը քանի տարեկան է, բայց պարզ է , որ յուրաքանչյուրի տարիքին ավելացել է 3 տարի, իսկ միասին կլինի` 3+3 : Այսպիսով` 40+3+3=46: 3 տարի հետո նրանց ընդհանուր տարիքը կլինի 46:
Պատ.` 46 տ.:
Ոչ ստանդարտ խնդիրների լուծման ժամանակ հաճախ օգտվում ենք այսպես կոչված «ենթադրությունների» մեթոդից.
Խնդիր.- Հարությունը, Դավիթը և Սուրենը միասին որսացել են 15 ձուկ: Հարությունը որսացել է այնքան ձուկ, որը հավասարապես կարելի է բաժանել 3 տղաների մեջ: Դավիթը Հարությունից 1 ձուկ ավելի էր որսացել, իսկ Սուրենը` բոլորից քիչ: Քանի՞ ձուկ է որսացել տղաներից յուրաքանչյուրը: [14]
Լուծում.- Ենթադրենք Հարությունը որսացել է 9 ձուկ, որը կարելի է հավասարապես բաժանել 3 տղաների մեջ: Այս դեպքում կստացվի, որ Դավիթը որսացել է ` 9+1, 10 ձուկ: Ուրեմն, Հարությունը և Դավիթը որսացել են 19 ձուկ` 9+10, որը հնարավոր չէ 1915: Ուրեմն, Հարությունը որսացել է 6 կամ 3 ձուկ: Ենթադրենք նա որսացել է 6 ձուկ, իսկ Դավիթը` 7 ձուկ, (6+1) : Միասին նրանք որսացել են 13 ձուկ` (6+7), նշանակում է Սուրենը որսացել է 2 ձուկ` (15-13)
| Սուրեն | Հարություն | Դավիթ |
|
|
|
|  9 9
19 | 9+1 15 |
| 2 |  6 6
13 | 6+1 15 |
| 8 |  3 3
7 | 3+1 15 |
Պատասխան` Հարությունը`6 ձուկ, Դավիթը` 7 ձուկ և Սուրենը` 2 ձուկ:



























 [ 8 ]
[ 8 ] Այս խնդիրը հեշտ է լուծել գծագրի միջոցով:
Այս խնդիրը հեշտ է լուծել գծագրի միջոցով:











