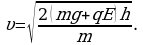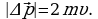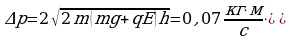Школьный этап олимпиады по физике.
11 класс
-
Баллистический маятник.
В ящик массой М, подвешенный на тонкой нити, попадает пуля массой m, летевшая горизонтально со скоростью 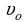 , и застревает в нем. На какую высоту Н поднимается ящик после попадания в него пули?
, и застревает в нем. На какую высоту Н поднимается ящик после попадания в него пули?
-
Баллистический маятник.
По условию первой задачи определите количество теплоты, выделившееся при ударе пули о ящик. Какую часть 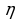 составляет это количество теплоты от первоначальной энергии пули?
составляет это количество теплоты от первоначальной энергии пули?
-
Пузырек воздуха.
На какой глубине h находился пузырек воздуха, если в процессе всплытия на поверхность воды, его радиус успел увеличиться в n = 2 раза? Атмосферное давление 100 кПа, плотность воды 1000 кг/м3. Температуру воды считать постоянной.
-
Аккумулятор.
Найдите ЭДС и внутреннее сопротивление аккумулятора, если при силе тока 15А он отдает во внешнюю цепь мощность 135 Вт, а при токе 6А – мощность 64,6 Вт.
-
Шарик и пластина.
Непроводящая отрицательно заряженная пластина, создающая вертикально направленное однородное электрическое поле напряженностью 104 В/м, укреплена горизонтально. На нее с высоты 10 см падает шарик массой 20 г, имеющий положительный заряд 10-5 Кл. Какой импульс шарик передает пластине при абсолютно упругом ударе?
Ответы, указания, решения к олимпиадным задачам
1. В ящик массой М, подвешенный на тонкой нити, попадает пуля массой m, летевшая горизонтально со скоростью 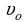 , и застревает в нем. На какую высоту Н поднимается ящик после попадания в него пули?
, и застревает в нем. На какую высоту Н поднимается ящик после попадания в него пули?
Решение.
-
Рассмотрим систему: ящик-нить-пуля. Эта система является замкнутой, но в ней внутренняя неконсервативная сила трения пули о ящик, работа которой не равна нулю, следовательно, механическая энергия системы не сохраняется.
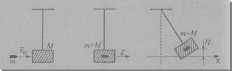
Выделим три состояния системы:
-
Первое – пуля движется со скоростью 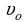 , ящик покоится.
, ящик покоится.
-
Второе - пуля застряла в ящике, ящик вместе с ней приобретает некоторую скорость u; нить вертикальна, т.к. время соударения мало.
-
Третье – ящик с пулей внутри поднялся на высоту Н; его скорость равна нулю.
-
При переходе системы из 1 состояния во 2 ее механическая энергия не сохраняется.
Поэтому во втором состоянии применяем закон сохранения импульса в проекции на ось Х: 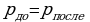 ;
; 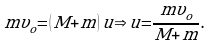
-
Закон сохранения энергии при переходе системы из второго в третье состояние: 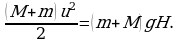
-
Решая систему уравнений, находим искомую величину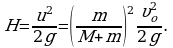
Критерии оценивания:
-
Выделение трех состояний системы, наличие рисунка к каждому состоянию – 2 балла
-
Запись закона сохранения импульса в проекции на ось Х, решение уравнения – 2 балла
-
Запись закона сохранения механической энергии – 2 балла
-
Решение системы двух уравнений – 3 балла
-
Вывод единиц измерения – 1 балл
2. По условию первой задачи определите количество теплоты, выделившееся при ударе пули о ящик. Какую часть 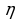 составляет это количество теплоты от первоначальной энергии пули?
составляет это количество теплоты от первоначальной энергии пули?
Решение.
-
При переходе указанной в задаче №1 системы из первого состояния во второе выделяется количество теплоты Q, равное со знаком минус работе сил трения между пулей и ящиком: 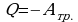
-
Согласно закону изменения механической энергии: 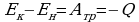 .
.
Отсюда искомое количество теплоты: 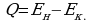
-
Начальная механическая энергия системы: 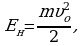 конечная -
конечная - 
-
Количество теплоты: 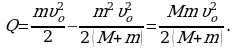
-
Определим ту часть механической энергии пули (т.е. первоначальной энергии системы), которая уходит на нагрев пули и ящика: 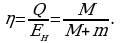
Критерии оценивания:
-
Составление формулы количества теплоты, равному со знаком минус работе силы трения между пулей и ящиком – 2 балла
-
Запись формулы количества теплоты, выделившегося при ударе пули о ящик в общем виде – 3 балла
-
Решение уравнения количества теплоты, выделившегося при ударе пули о ящик – 4 балла
-
Нахождение части механической энергии пули, которая идет на нагрев пули и ящика – 1 балл
3. На какой глубине h находился пузырек воздуха, если в процессе его всплытия на поверхность воды его радиус успел увеличиться в n = 2 раза? Атмосферное давление 100 кПа, плотность воды 1000 кг/м3. Температуру воды считать постоянной.
Решение.
-
Считаем, что температура воздуха внутри пузырька не меняется, т.е. он вплывает достаточно медленно, тогда справедлив закон Бойля-Мариотта: 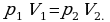
-
Давление воздуха внутри пузырька на глубине h равно сумме атмосферного и гидростатического давлений: 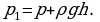
-
Давление на поверхности воды равно атмосферному давлению: 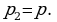
-
Начальный объем пузырька: 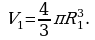 Конечный -
Конечный - 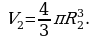
-
Подставим, получим: 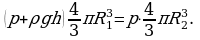
-
С учетом условия 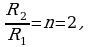 получим:
получим: 
-
Отсюда искомая глубина: 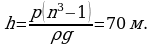
Критерии оценивания:
-
Запись уравнения закона Бойля-Мариотта – 1 балл
-
Запись уравнения давления воздуха на глубине h – 1 балл
-
Запись уравнения давления воздуха на поверхности воды – 1 балл
-
Формулы начального и конечного объемом пузырьков – 2 балла
-
Вывод расчетной формулы в общем виде – 4 балла
4. Найдите ЭДС и внутреннее сопротивление аккумулятора, если при силе тока 15А он отдает во внешнюю цепь мощность 135 Вт, а при токе 6А – мощность 64,6 Вт.
Решение.
-
Воспользуемся соотношением для полезной мощности:  где
где 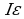 - полная мощность, а
- полная мощность, а 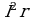 - потери мощности в источнике.
- потери мощности в источнике.
-
Тогда имеем систему уравнений: 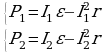
-
Решая систему уравнений, получаем: 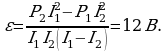
-
Умножим (1) на 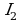 , а (2) на
, а (2) на 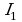 , а затем вычтем и получим:
, а затем вычтем и получим: 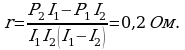
Критерии оценивания:
-
Уравнение для полезной мощности – 1 балл
-
Составление системы уравнений – 2 балла
-
Решение системы уравнений, вывод формулы в общем виде – 3 балла
-
Нахождение внутреннего сопротивления источника тока – 3 балла
-
Математические вычисления – 1 балл
5. Непроводящая отрицательно заряженная пластина, создающая вертикально направленное однородное электрическое поле напряженностью 104 В/м, укреплена горизонтально. На нее с высоты 10 см падает шарик массой 20 г, имеющий положительный заряд 10-5 Кл. Какой импульс шарик передает пластине при абсолютно упругом ударе?
Решение.
-
Поскольку пластина заряжена отрицательно, напряженность поля над ней направлена вертикально вниз, поэтому при падении шарика на него действуют две сонаправленные силы: сила тяжести и электрическая
и электрическая 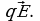
-
Перемещая шарик на расстояние h, они совершают работу: 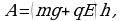 что по теореме о кинетической энергии приводит к приобретению конечной скорости
что по теореме о кинетической энергии приводит к приобретению конечной скорости 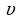 :
: 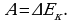
-
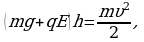 и
и 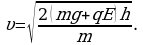
-
При абсолютно упругом ударе скорость шарика не изменится по модулю, но изменится по направлению на противоположное, что соответствует изменению импульса, по модулю равного: 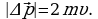
-
Такой импульс он и передаст пластине: 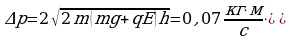
Критерии оценивания:
-
Запись второго закона Ньютона в векторной форме – 1 балл
-
Запись формулы работы сил – 1 балл
-
Запись теоремы о кинетической энергии - 1 балл
-
Решение системы уравнений – 3 балла
-
Нахождение импульса, переданного телом, вывод формулы в общем виде – 2 балла
-
Вывод единиц измерения – 1 балл
-
Математические вычисления – 1 балл





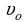 , и застревает в нем. На какую высоту Н поднимается ящик после попадания в него пули?
, и застревает в нем. На какую высоту Н поднимается ящик после попадания в него пули?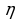 составляет это количество теплоты от первоначальной энергии пули?
составляет это количество теплоты от первоначальной энергии пули?
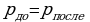 ;
; 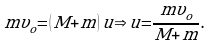
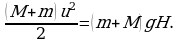
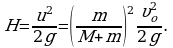
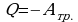
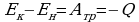 .
. 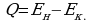
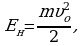 конечная -
конечная - 
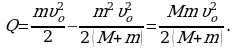
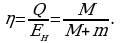
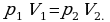
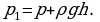
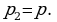
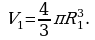 Конечный -
Конечный - 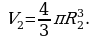
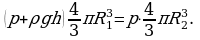
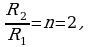 получим:
получим: 
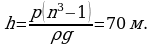
 где
где 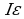 - полная мощность, а
- полная мощность, а 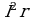 - потери мощности в источнике.
- потери мощности в источнике.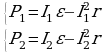
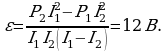
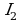 , а (2) на
, а (2) на 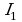 , а затем вычтем и получим:
, а затем вычтем и получим: 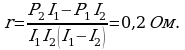
 и электрическая
и электрическая 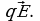
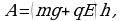 что по теореме о кинетической энергии приводит к приобретению конечной скорости
что по теореме о кинетической энергии приводит к приобретению конечной скорости 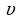 :
: 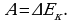
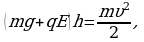 и
и