Олимпиадные задачи по математике (7 – 8 класс) с решением.

ОЛИМПИАДНЫЕ ЗАДАЧИ 7 – 8 КЛАСС

1. Разность между квадратом суммы и суммой цифр двухзначного числа равна самому числу. Найти все такие числа.

Решение. (a+b)² – (b+a) = 10a+b

(a+b)*(a+b-2) = 9a

(a+b) = 9, т.к. (a+b) не равно a

(a+b-2) = a, b = 2, a = 7

Ответ: 72

1. Может ли число, в записи которого участвуют 2010 цифр 3 (тройка) и несколько нулей, быть полным квадратом?

Решение. Допустим, что изначальное число - полный квадрат, тогда оно будет заканчиваться на четное количество нулей. Разложим его на множители – представим в виде произведения десятки в четной степени и числа, заканчивающегося на три. Т.к. второе число в произведении заканчивается на три и не может быть представлено в виде квадрата, то и изначальное число не может быть представлено в виде полного квадрата.

Ответ: не может быть полным квадратом.

Свойства квадрата целого числа:

1. Квадрат числа при делении на любое число дает тот же остаток, что и квадрат его остатка.

2. Точный квадрат целого числа не может оканчиваться цифрами 2, 3, 7, 8, а также нечётным количеством нулей.
   Первое свойство очевидное и доказательства не требует.

Квадрат натурального числа либо делится на 4, либо при делении на 8 даёт остаток 1.
Доказательство:
Если а – число чётное, то есть а = 2к, то 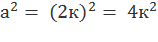_{ }  – делится на 4.
Если а – число нечётное, то есть а = 2к + 1, то
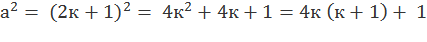_{ } – при делении на 8 даёт остаток 1.

Квадрат натурального числа либо делится на 9, либо при делении на 3 даёт остаток 1.
Доказательство:
Если число а кратно 3, значит а = 3к, тогда 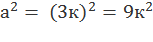_{ } - делится на 9.
Если же число а не кратно 3, то оно имеет вид а = 3к ± 1,

Тогда

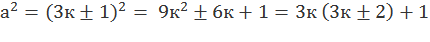
– при делении на 3 даёт остаток 1.

Число это делится на 3, но не делится на 9. А было бы квадратом - делилось.

1. На рисунке 1 =70° + x – y.

1 – 2 =50°+ 2х – 2у. Доказать, что МВ BN.

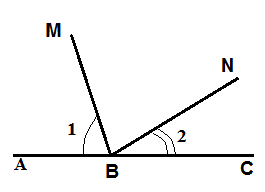
Доказательство:

2 = 1 – (50° + 2х – 2у) = 70° + x - y - 50° - 2x + 2y = 20° - x + y, тогда

1 + 2 = 70° + x - y + (20° - x + y = 90°.

Значит MBN = 180° - ( 1 + 2) = 90°, т. е. МВ BN.

Что и требовалось доказать.