Методическая разработка открытого урока

Аннотация

В данной методической разработке представлена методика проведения комбинированного занятия по теме «Преобразование графиков тригонометрических функций» дисциплины «Математика».

Методическая разработка содержит:

• План урока.

• Методику проведения урока.

• Рабочую тетрадь по теме «Преобразование графиков тригонометрических функций».

• Карточки с тестовыми заданиями.

• Карточки « Самооценка уровня усвоения изученного материала».

• Слайды с учебно-методическим материалом урока.

При проведении занятия широко используются возможности интерактивной доски. Учебно-методический материал занятия отображается на интерактивной доске и включает в себя как задания, разработанные препедавателем так и анимационный и интерактивный материал с обучающего диска. Слайды подготовлены в среде мастера SMART Notebook 10.

Данная методическая разработка может представлять интерес для преподавателей различных дисциплин при подготовке и проведении занятий с использованием интерактивной доски.

Содержание

Введение

План урока

Методика проведения урока

Заключение

Приложение 1.

Введение

Российский национальный проект «Образование» включает в себя такие важные вопросы как применение инноваций и интерактивного оборудования.

XXI век - век новых информационных технологий. С раннего возраста дети уже привыкают к удобствам технического прогресса и современным средствам получения информации. И с этим ничего не поделаешь, так гораздо легче воспринимать информацию.

Новые информационно-коммуникационные средства обучения приходят на смену классическим. Применение информационных технологий на занятиях направлено на совершенствование существующих технологий обучения, их использование расширяет стандартные методы обучения.

Одним из таких средств является интерактивная доска. Ее использование на уроках позволяет многим преподавателям плавно перейти от привычного ведения занятия к современному уровню преподавания, а учащимся успешно овладевать знаниями.

Работа с интерактивными досками помогает в организации учебного процесса. Это хороший выбор для тех преподавателей, которые с помощью современных технических и аудиовизуальных средств и интенсивных методов обучения хотят заинтересовать своих слушателей, облегчить усвоение материала. С интерактивными досками можно работать как в большой аудитории, так и в маленьких группах. Эти современные аудиовизуальные средства обучения помогают разнообразить занятие.

Преподаватель может по-разному классифицировать материал, используя различные возможности доски: перемещать объекты, работать с цветом, – при этом, привлекая к процессу студентов, которые затем могут самостоятельно работать в небольших группах. Иногда можно снова обращать внимание учащихся на доску, чтобы они поделились своими мыслями и обсудили их перед тем, как продолжить работу. Но важно понимать, что этот эффективность работы с доской во многом зависит от самого преподавателя, от того, как он применяет те или иные ее возможности.

Данная методическая разработка содержит материалы, иллюстрирующие разнообразие и возможности использования интерактивной доски в учебном процессе.

План открытого урока

по дисциплине «Математика

Дата проведения: 29.10.2013 г.

Занятие: 21

Группа: 118

Специальность:

110809 « Механизация с/х»

Преподаватель: Мигашкина О. А.

Место проведения: аудитория №102

Тема: Преобразование графиков тригонометрических функций.

Вид занятия (тип урока): комбинированный урок

Цели урока:

Образовательная: повторить правила преобразований графиков функций; рассмотреть виды преобразований графиков тригонометрических функций, отработать навыки построения графиков функций.

Развивающая: способствовать формированию умений использовать приёмы сравнения, обобщения, выявления главного, переноса знаний в новую ситуацию; развитию математического кругозора, мышления, внимания и памяти.

Воспитательная: содействовать воспитанию интереса к математике, активности, формированию коммуникативных навыков при организации групповой работы студентов.

Методы и приёмы обучения:

- информационно-развивающий (объяснение, рассказ);

- наглядно-иллюстративный (демонстрация слайдов);

- репродуктивный ( решение задач и тестовых заданий);

- проблемный.

Межпредметные связи: физика, биология

Внутрипредметные связи: Тема «Преобразование графиков функций»

Тема «Функция , свойства, график».

Тема «Функция , свойства, график».

Тема «Функции свойства, графики».

Обеспечение занятия:

Наглядные пособия:

• Слайды с учебно-методическим материалом.

• Анимационный и интерактивный материал с обучающего диска.

Раздаточный материал:

• Карточки с тестовыми заданиями

• Карточки « Самооценка уровня усвоения изученного материала»

• Шаблоны систем координат для работы в группах

• Рабочая тетрадь

ТСО:

• Персональный компьютер IBM PC

• Мультимедийный проектор и интерактивная доска.

Литература:

• Алгебра и начала математического анализа. 10-11 классы: учеб. для общеобразоват. учреждений с прил. на электронном носителе/ [А. Н. Колмогоров, А. М. Абрамов, Ю. П. Дудницын и др. ]; под ред. А. Н. Колмогорова. – 21-е изд. – М.: Просвещение, 2012. – 384 с.

• Практические занятия по математике: Учеб. пособие для средних спец. учеб. заведений/ Н. В. Богомолов. – 5-е изд., стер. – М. : Высш. шк., 2002. – 495 с.

Требования к усвоениям учебного материала:

Студент должен

Знать: графики тригонометрических функций, геометрические преобразования графиков тригонометрических функций.

Уметь: применять геометрические преобразования при построении графиков тригонометрических функций.

Общие компетенции:

ОК 3. Принимать решения в стандартных и нестандартных ситуациях и нести за них ответственность.

ОК 6. Работать в коллективе и команде, эффективно общаться с коллегами, руководством, потребителями.

ОК 7. Брать на себя ответственность за работу членов команды (подчиненных), за результат выполнения заданий.

Содержание занятия:

1.Организационный момент (2 мин)

• Приветствие

• Определение отсутствующих

• Проверка готовности группы к занятию

• Организация внимания студентов.

2.Проверка знаний и умений по пройденной теме (10 мин)

2.1. Выполнение задания на установление соответствия «формула-график»

2.2.Решение теста

3. Мотивация учебной деятельности. (2 мин)

4. Сообщение темы, плана, постановка цели занятия (2 мин)

5. Актуализация опорных знаний и действий студентов (20 мин)

5.1.Графики каких функций вы умеете строить?
5.2.Установите соответствие между формулой, задающей функцию и названием графика.

5.3. Преобразование графиков квадратичной функции.

6. Изучение и освоение нового материала (восприятие, осмысление)

(30 мин)

6.1. Виды преобразований графиков тригонометрических функций.

6.2. Построение графиков функций.

7. Закрепление изученного материала (20 мин)

7.1.Построение графиков функций (работа в группах).

8. Подведение итогов урока (3 мин)

8.1. Заполнение карточки «Самооценка уровня усвоения изученного материала)

8.2. Оценивание

9. Сообщение домашнего задания: (1 мин)

Построить графики функций

Методика проведения урока

1. Организационный момент

Приветствие. Преподаватель и студенты приветствуют друг друга.

Определение отсутствующих студентов. Дежурный сообщает об отсутствующих студентах. Преподаватель отмечает отсутствующих в журнале.

Проверка готовности группы и организация внимания студентов. Преподаватель настраивает студентов на серьёзный лад, предлагает им сосредоточиться и быть внимательными на протяжении всего урока. Создаёт непринуждённую, но рабочую атмосферу на уроке.

1. Проверка знаний и умений по пройденной теме

1. Преподаватель предлагает студентам выполнить устное задание на установление соответствия «формула-график» на интерактивной доске с использованием маркера. (Презентация, слайд 1)

2. На втором этапе проверки знаний и умений по пройденной теме студенты выполняют тестовые задания «Да-нет». (Приложение 1.) Ответ проверяют составлением ответа на интерактивной доске (маркером чертится кривая-ответ, ответу «да» соответствует кривая над прямой, «нет» - кривая под числовой прямой). (Презентация, слайд 2). Происходит повторное проговаривание правильных ответов. Студенты получают листы самооценки на урок, в которых будут проставлять количество заработанных баллов на протяжении всего занятия.

(Приложение 1)

1. Мотивация учебной деятельности

Преподаватель, после проверки тестового задания акцентирует внимание студентов на получившуюся кривую: «Встречали ли вы в своей жизни такие графики?»

Осуществляется показ презентации «Графики тригонометрических функций в жизни», который сопровождается пояснениями преподавателя. Просмотр презентации завершается вопросом: «Как вы думаете, какова тема нашего занятия?» (Презентация, слайд 5-9)

1. Сообщение темы, плана, постановка цели занятия

Сообщается тема урока и формулируются цели урока. Рекомендуется план урока, который включает в себя следующие пункты:

1. Виды преобразований графиков тригонометрических функций.

2. Построение графиков функций.

Преподаватель объясняет студентам, что работа на уроке будет осуществляться в рабочих тетрадях.

При сообщении темы урока и плана демонстрируются 10 слайд презентации

1. Актуализация опорных знаний и действий студентов

Преподаватель задаёт вопрос: «Графики каких функций вы умеете строить?»

Прогнозируемый ответ – графики линейных, квадратичных, тригонометрических……функций.

Студентам предлагается выполнить задание на интерактивной доске «Установите соответствие между формулой, задающей функцию и названием графика». (Презентация, слайд 3).

По слайдам презентации студенты вспоминают преобразование графиков квадратичной функции, отвечая на вопросы (Слайд 4):

- Какие преобразования нужно выполнить, чтобы получить график функции?

Прогнозируемый ответ – совершить параллельный перенос графика функции на 2 единичных отрезка вверх по оси х.

- Каким образом построить график функции
Прогнозируемый ответ – выполнить параллельный перенос графика функции на вектор (0; -2).

По такому же алгоритму студенты вспоминают построение графиков следующих функций

Преподаватель предлагает проверить правильность рассуждений с помощью анимационного материала с обучающего диска.

Студенты делают вывод о том, какие виды преобразований графиков функции они вспомнили.

Преподаватель задаёт вопрос: «Как вы думаете, такие преобразования применимы к графикам тригонометрических функций?

Прогнозируемый ответ – да, наверное.

1. Изучение и освоение нового материала

Вопрос 1. Виды преобразований графиков тригонометрических функций

Преподаватель задаёт вопрос: «Каким образом построить график функции (Слайд 12)

• График какой функции нужно построить, как основу?

(Студенты выполняют построение графика по контрольным точкам – ).

Построение графика функции студенты выполняют по желанию на интерактивной доске, остальные в рабочей тетради в готовой системе координат. (Слайд 13)

Преподаватель предлагает построить график следующей функции – Построение выполняется на интерактивной доске и в рабочих тетрадях. (Слайд 13)

После построения графиков преподаватель просит студентов сделать вывод о рассмотренных преобразованиях графиков. (Параллельный перенос графиков функций на вектор (0; в) вдоль оси ординат). (Слайд 14)

Для закрепления преподаватель предлагает студентам выполнить задание на интерактивной доске и в рабочих тетрадях. (Слайд 15)

Далее перед учащимися возникает вопрос, а как же построить график функции , (Слайд 16)

Изучение происходит по такому же алгоритму, с использованием интерактивной доски и рабочей тетради. Правильность построения проверяется с помощью анимации с обучающего диска. Студенты делают вывод о виде преобразования –параллельный перенос вдоль оси абсцисс. (Слайды 17-19)

Преподаватель нацеливает студентов на выполнение заданий на интерактивной доске и в рабочей тетради.

И опять перед студентами вопрос: «Какие преобразования необходимо использовать при выполнении заданий 5 и 6? (Приложение 3, слайд 20).

Предполагаемый ответ-растяжение и сжатие относительно координатных осей.

Преподаватель предлагает понаблюдать за преобразованием графика используя анимацию «Построение », но график функции предлагает построить студентам без анимации, используя интерактивную доску.

Студенты формулируют вывод: « для построения графика функции надо растянуть график функции в а раз вдоль оси ординат.

Если то растяжение – сжатие в а раз.( Слайд 21)

Далее учащиеся выполняют задания в рабочих тетрадях 5 и 6 и на интерактивной доске (задания на установление соответствий). (Слайды 22-24)

Вопрос 2. Построение графиков функций.

- Итак, мы построили много графиков функций, назовите виды преобразований, которые были рассмотрены.

- Какие преобразования нужно применить, чтобы построить график функции ? (Слайд 25-26)

Один студент выполняет построение на доске, остальные в тетради.

Проверка правильности построения осуществляется с помощью интерактивной модели с обучающего диска.

1. Закрепление изученного материала

Студенты делятся на 5 групп, каждая группа получает задание на построение графика функции и готовый шаблон системы координат (приложение 4), на которой группа должна отобразить общее решение задания. При выполнении этого задания каждый участник выполняет построение и в своей карточке (рабочая тетрадь).

Итогом выполнения задания является защита построенного графика каждой группой. (Слайд 27)

1. Подведение итогов урока

Студентам предлагается оценить свою работу на занятии с помощью карточки «Самооценка уровня усвоения изученного материала», в которой на протяжении всего урока каждый учащийся отмечал набранные баллы по каждому этапу урока. По общему количеству баллов учащийся выставляет себе соответствующую оценку и озвучивает её.

1. Сообщение домашнего задания

Студентам предлагается записать домашнее задание (слайд 29-30):

Построить графики функций

Заключение

В данной работе рассмотрены возможности применения интерактивной доски на уроке математики. Данное средство можно использовать:

1)  на этапе введения нового материала.

2)  на этапе формирования образа, подкрепляющего понятие.

3)  на этапе мысленных манипуляций созданным образом при решении задач.

4)  для связи образной и аналитической составляющих мышления.

Использование интерактивного оборудования позволяет заменить многие традиционные средства обучения. Во многих случаях такая замена оказывается эффективной, так как позволяет поддерживать у студентов интерес к изучаемому предмету, позволяет создать информационную обстановку, стимулирующую интерес и пытливость учащегося. Интерактивное оборудование даёт возможность преподавателю оперативно сочетать разнообразные средства, способствующие более глубокому и осознанному усвоению изучаемого материала, экономит время урока.

На момент написания методической разработки урок был проведён в четырёх группах, в одной из них в качестве открытого урока. Студенты с удовольствием выполняют задания на интерактивной доске. Нужно заметить, что в каждой группе находится несколько студентов, которые испытывают «боязнь» перед интерактивной доской, но это всё проходит после выполнения одного, двух заданий с использованием этого средства.

Считаю, что весь урок в целом, и отдельные его элементы, имеют место для дальнейшего совершенствования и использования при изучении дисциплины «Математика». А также может представлять интерес для преподавателей других дисциплин, использующих интерактивную доску.

Приложение 1.

Лист самоконтроля

Фамилия Имя_________________________________________

Тест (балл)	3 Задание (балл)	5 Задание (балл)	6 задание (балл)	Ответы на вопросы (устно)	Работа у доски, работа в группах	Итоговая оценка
5 заданий-5 4 задания-4 3 задания-3 2 задания-2 1 задание-1	3 графика-3 2 графика -2 1 график -1	4 графика-4 3 графика-3 2 графика-2 1 график -1	4 графика-4 3 графика-3 2 графика-2 1 график -1	За каждый правильный ответ- 1 балл	2 балла 4 балла	20-25 б. - «5» 15-20 б. – «4» 10-15 б. – «3» Менее 10 б. – «2»

Приложение 2.

Тест

1 Вариант

1. Функция синус чётная?

2. График функции косинус симметричен относительно оси Оу?

3. Область значений функций синус и косинус ?

4. График тангенса проходит через начало координат?

5. Функция котангенс чётная?

2 Вариант

1. Функция косинус нечётная?

2. График функции синус симметричен относительно начала координат?

3. Область значений функций тангенс и котангенс ?

4. График котангенса не проходит через начало координат?

5. Функция тангенс чётная?

Приложение 3.

Рабочая тетрадь

Преобразование графиков тригонометрических функций

План

1. Виды преобразований графиков тригонометрических функций.

2. Построение графиков функций.

1. Задание.

Установите соответствие:

y = f(x) + m растяжение относительно оси Оу

y = f(x + t) параллельный перенос

относительно оси Оу

y = af(x)

растяжение относительно оси Ох

y = fа(x) параллельный перенос

относительно оси Оу

2. Задание

Постройте график функции

3. Задание

Установите соответствие «формула-график»

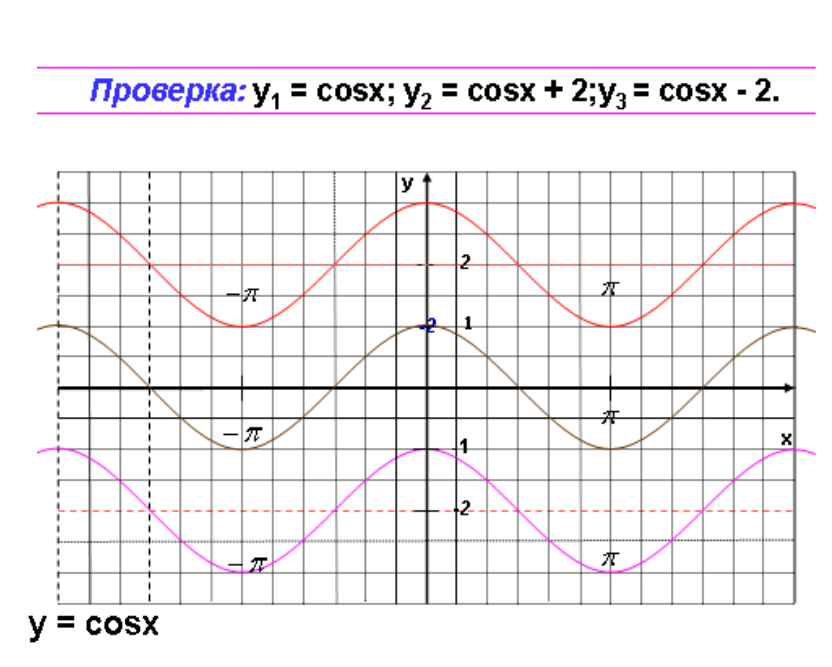
4. Задание

Постройте график функции

5. Задание

Определите, графики каких функций изображены на рисунке:

6. Задание

7. Задание Постройте

8. Задание

Постройте график функции

9 Задание.

Установи соответствие

Приложение 4.

Раздаточный материал для работы в группах

Приложение 5.

Слайды с учебно-методическим материалом

Литература

1. Н. В. Богомолов. Практические занятия по математике: Учеб. пособие для средних спец. учеб. заведений – 5-е изд., стер. – М. : Высш. шк., 2002. – 495 с.

1. Гусев В. А., Мордкович А. Г. Математика: Справ. Материалы: Кн. для учащихся.-2-е изд.-М.: Просвещение, 2000.-416 с.

1. Алгебра и начала математического анализа. 10-11 классы: учеб. для общеобразоват. учреждений с прил. на электронном носителе/ [А. Н. Колмогоров, А. М. Абрамов, Ю. П. Дудницын и др. ]; под ред. А. Н. Колмогорова. – 21-е изд. – М.: Просвещение, 2012. – 384 с.

http://nsportal.ru/sites/default/files/2012/10/urokalgebryiv10klasse.doc