Описанная окружность_урок1

Описанная окружность

Определение: окружность называется описанной около треугольника,

если все вершины треугольника

лежат на этой окружности.

На каком рисунке окружность описана около треугольника:

1)

2)

3)

4)

5)

Если окружность описана около треугольника,

то треугольник вписан в окружность.

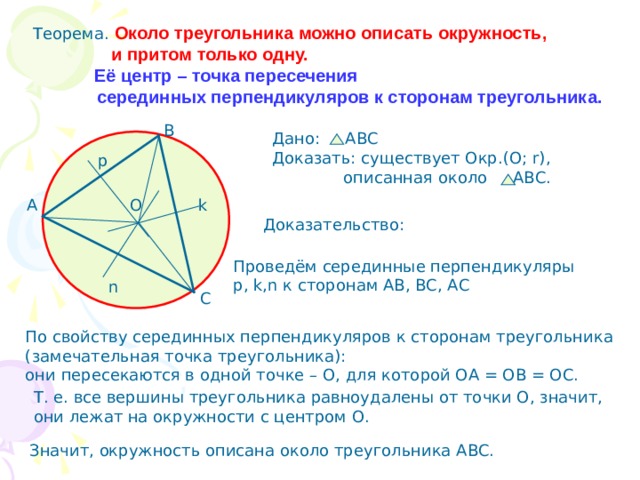
Теорема. Около треугольника можно описать окружность,

и притом только одну.

Её центр – точка пересечения

серединных перпендикуляров к сторонам треугольника.

В

Дано: АВС

Доказать: существует Окр.(О; r) ,

описанная около АВС.

p

k

О

А

Доказательство:

Проведём серединные перпендикуляры

p, k,n к сторонам АВ, ВС, АС

n

С

По свойству серединных перпендикуляров к сторонам треугольника

( замечательная точка треугольника):

они пересекаются в одной точке – О, для которой ОА = ОВ = ОС.

Т. е. все вершины треугольника равноудалены от точки О, значит,

они лежат на окружности с центром О.

Значит, окружность описана около треугольника АВС.

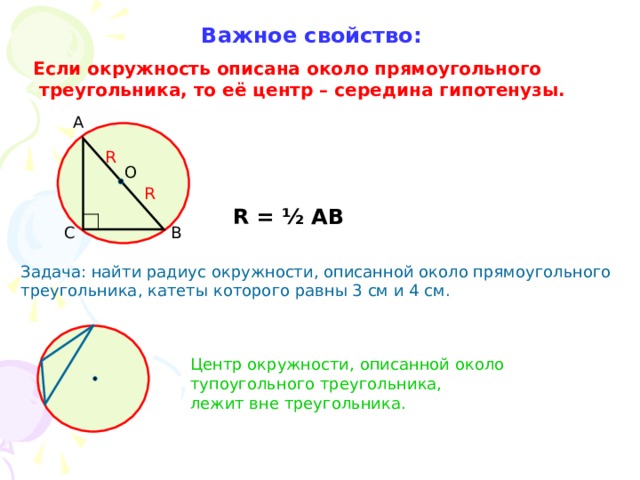
Важное свойство:

Если окружность описана около прямоугольного

треугольника, то её центр – середина гипотенузы.

A

R

O

R

R = ½ AB

C

B

Задача: найти радиус окружности, описанной около прямоугольного

треугольника, катеты которого равны 3 см и 4 см.

Центр окружности, описанной около тупоугольного треугольника,

лежит вне треугольника.

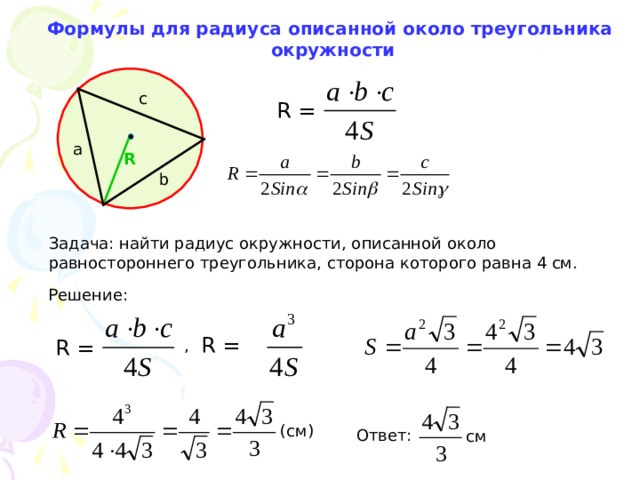
Формулы для радиуса описанной около треугольника

окружности

c

R =

a

R

b

Задача: найти радиус окружности, описанной около

равностороннего треугольника, сторона которого равна 4 см.

Решение:

R =

R =

,

(см)

Ответ:

см

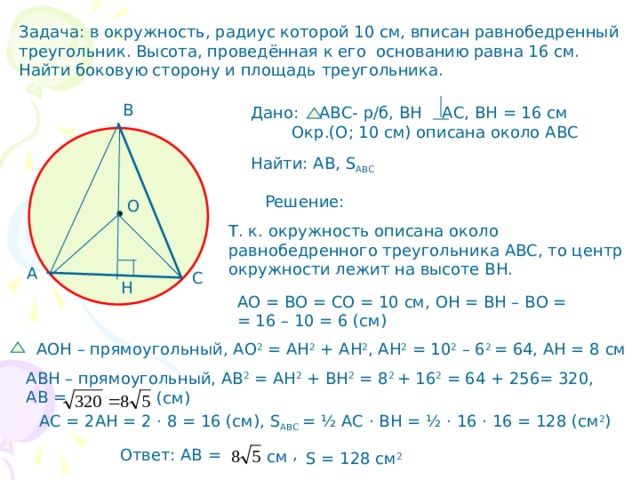
Задача: в окружность, радиус которой 10 см, вписан равнобедренный треугольник. Высота, проведённая к его основанию равна 16 см. Найти боковую сторону и площадь треугольника.

В

Дано: АВС- р/б, ВН АС, ВН = 16 см

Окр.(О; 10 см) описана около АВС

Найти: АВ, S АВС

Решение:

О

Т. к. окружность описана около

равнобедренного треугольника АВС, то центр

окружности лежит на высоте ВН.

А

С

Н

АО = ВО = СО = 10 см, ОН = ВН – ВО =

= 16 – 10 = 6 (см)

АОН – прямоугольный, АО 2 = АН 2 + АН 2 , АН 2 = 10 2 – 6 2 = 64, АН = 8 см

АВН – прямоугольный, АВ 2 = АН 2 + ВН 2 = 8 2 + 16 2 = 64 + 256= 320,

АВ =

(см)

АС = 2АН = 2 · 8 = 16 (см), S АВС = ½ АС · ВН = ½ · 16 · 16 = 128 (см 2 )

,

Ответ: АВ =

см

S = 128 см 2