Описанная окружность_урок2

Описанная окружность

Определение: окружность называется описанной около

четырёхугольника,

если все вершины четырёхугольника лежат на окружности.

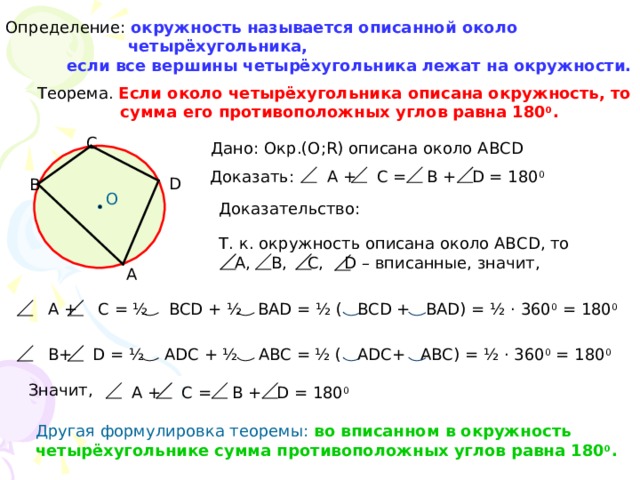
Теорема. Если около четырёхугольника описана окружность, то

сумма его противоположных углов равна 180 0 .

C

Дано: Окр.(О; R) описана около АВС D

A + C = B + D = 180 0

Доказать:

D

B

О

Доказательство:

Т. к. окружность описана около АВС D , то

А, В, С, D – вписанные, значит,

A

А + C = ½ BCD + ½ BAD = ½ ( BCD + BAD) = ½ · 360 0 = 180 0

B+ D = ½ ADC + ½ ABC = ½ ( ADC+ ABC) = ½ · 360 0 = 180 0

Значит,

A + C = B + D = 180 0

Другая формулировка теоремы: во вписанном в окружность

четырёхугольнике сумма противоположных углов равна 180 0 .

Обратная теорема: если сумма противоположных углов

четырёхугольника равна 180 0 , то около

него можно описать окружность.

C

Дано: АВС D, A + C = 180 0

D

B

О

Доказать:

Окр.(О; R) описана около АВС D

Доказательство: № 729 (учебник)

A

Вокруг какого четырёхугольника нельзя описать окружность?

Следствие 1: около любого прямоугольника можно описать

окружность, её центр – точка пересечения диагоналей.

Следствие 2: около равнобедренной трапеции можно описать

окружность.

А

В

С

К

Реши задачи

Найти углы четырёхугольника РКЕН:

В

Е

С

?

К

120 0

70 0

?

О

80 0

80 0

М

А

Р

Н