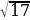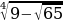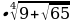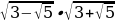Корни натуральной степени из числа и их свойства.
Определение. Корнем n-ной степени из числа a называется такое число, n-я степень которого равна a, то есть 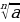 = b, т.к.
= b, т.к. 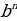 = a
= a
Если n - нечетное число, то существует единственный корень n-й степени из любого числа (положительного или отрицательного).
Например, 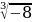 = – 2,
= – 2, 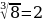
Если n - четное число, то существует два корня n-й степени из любого положительного числа. Например, корень четвертой степени из числа 625 - это числа – 5 и 5. Так как 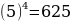 ,
, 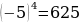
Корень четной степени из отрицательного числа не существует. Например, 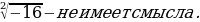
Определение. Арифметическим корнем n-ной степени из числа а называют неотрицательное число, n-я степень которого равна a.
Например, 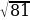 = 9 т.к.
= 9 т.к. 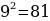
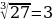 т.к.
т.к. 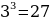
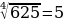 т.к.
т.к. 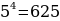
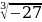 = – 3 т.к.
= – 3 т.к. 
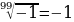 т.к.
т.к. 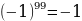
Решение уравнения хn = a
n – нечетное
При любых значениях a уравнение имеет один корень
n – четное
-
Если a  0, то уравнение имеет два корня
0, то уравнение имеет два корня
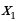 =
= 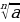 ;
; 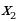 =
= 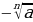
-
Если a  0 , то уравнение имеет один корень x = 0
0 , то уравнение имеет один корень x = 0
-
Если a  0 , то уравнение не имеет корней
0 , то уравнение не имеет корней
Основные свойства арифметических корней n-ной степени
Для любого натурального n, целого k и любых неотрицательных чисел a и b выполнены равенства:
1 .
. 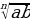 =
= 
2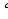 .
. 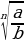 =
= 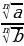 (
(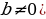
3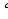 .
. 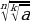 =
= 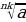
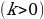
4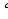 .
. 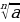 =
= 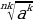
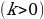
5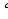 .
. 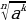 =
= 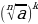 (если
(если 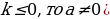
6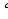 . Для любых чисел a и b , таких, что
. Для любых чисел a и b , таких, что 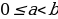 , выполняется неравенство
, выполняется неравенство 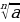

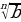
Примеры с решениями:
1. Решите уравнения
а) 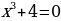
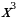 = – 4
= – 4
х = 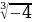 =
= 
б) 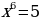
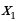 =
=  ;
; 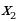 =
= 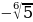
в) 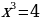
х = 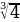
г) 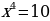
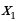 =
= 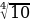 ;
; 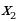 =
= 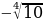
2. Найдите значения числового выражения
а) 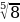
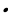
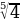 =
= 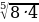 =
= 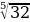 = 2
= 2
б) 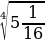 =
= 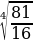 =
= 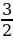
Решите самостоятельно:
1) Вычислите
а) 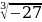
б) 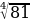
в) 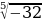
г) 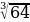
2) Решите уравнения
а) 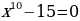
б) 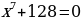
в) 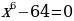
г) 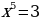
3) Найдите значение числового выражения
а) 
б) 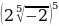
в) (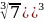
г) 
д) 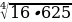
е)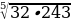
ж) 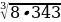
з) 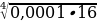
и) 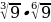
к) 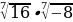
л) 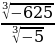
м) 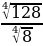
4) Найдите значение выражения
Воспользуйтесь формулой сокращенного умножения:
(a−b)·(a + b) = a2 − b2
а) 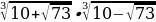
б) 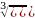 +
+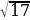
в) 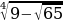
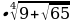
г) 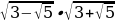
Ответьте на вопросы:
– Дайте определение корня n-ой степени из действительного числа.
– Сколько корней может иметь уравнение вида хn = a?
Отчего это зависит?
– Как вычислить корень n-ой степени из числа?
– Когда корень n-ой степени не имеет смысла?







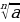 = b, т.к.
= b, т.к. 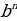 = a
= a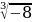 = – 2,
= – 2, 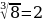
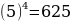 ,
, 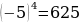
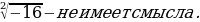
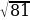 = 9 т.к.
= 9 т.к. 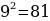
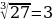 т.к.
т.к. 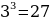
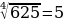 т.к.
т.к. 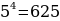
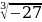 = – 3 т.к.
= – 3 т.к. 
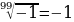 т.к.
т.к. 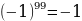
 0, то уравнение имеет два корня
0, то уравнение имеет два корня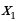 =
= 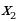 =
= 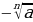
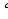 .
. 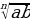 =
= 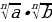
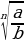 =
= 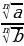 (
(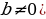
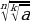 =
= 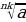
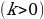
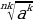
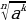 =
= 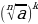 (если
(если 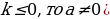
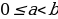 , выполняется неравенство
, выполняется неравенство 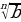
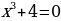
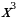 = – 4
= – 4 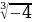 =
= 
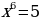
 ;
; 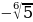
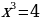
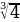
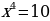
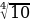 ;
; 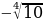
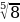
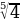 =
= 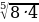 =
= 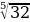 = 2
= 2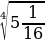 =
= 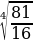 =
= 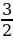
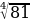
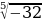
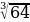
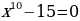
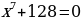
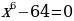
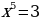
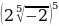
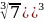
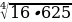
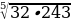
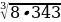
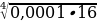
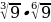
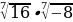
 +
+