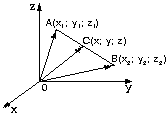Данный краткий конспект отражает такие важные понятия: прямоугольная система кокоординат, координаты точки в пространстве, вектор, действия над векторами, косинус угла между векторами
Просмотр содержимого документа
«Опорный конспект по теме: "Координатный метод в пространстве".11 класс»
Тема: «Векторы в пространстве. Метод координат в пространстве».
| 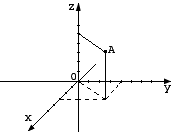
рис. 1
| Если через некоторую точку пространства проведены три попарно перпендикулярные прямые, на каждой из них выбрано направление (оно обозначается стрелкой) и выбрана единица измерения отрезков, то говорят, что задана прямоугольная система координат в пространстве. Пример. Точка А ( 3; 4; 5), рис.1.
Ох, Оу, Оz - оси абсцисс, ординат и аппликат. Координаты точки М записываются так: М (х; у; z). |
| 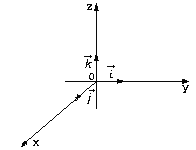
рис. 2
| Зададим в пространстве прямоугольную систему координат Оxyz. На каждой из положительных полуосей отложим от начала координат единичные векторы (длины которых равны единице): 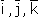 ., рис.2. ., рис.2.
Эти векторы назовем координатными векторами, они не компланарны( т.е. не лежат в одной плоскости). Поэтому любой вектор а можно разложить по координатным векторам, т.е. представить в виде:
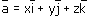
причем коэффициенты разложения х, у, z определяются единственным образом.
|
Коэффициенты x, y и z в разложении называются координатами вектора 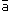 в данной системе координат.
в данной системе координат.
Координаты вектора 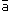 будем записывать в скобках:
будем записывать в скобках: 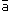 (x ; y ; z).
(x ; y ; z).
Координаты равных векторов равны.
Правила действия над векторами.
Каждая координата суммы двух или более векторов равна сумме соответствующих координат этих векторов. Если 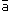 +
+  =
= 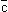 ,
,
то 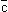 (x
(x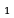 +x₂; y₁+y₂; z₁+z₂); где
+x₂; y₁+y₂; z₁+z₂); где 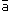 (x₁; y₁; z₁),
(x₁; y₁; z₁),  {x₂; y₂; z₂}.
{x₂; y₂; z₂}.
Каждая координата разности двух векторов равна разности соответствующих координат этих векторов. Если 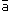 -
-  =
= 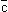 , то
, то 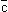 (x₁-x₂; y₁-y₂; z₁-z₂).
(x₁-x₂; y₁-y₂; z₁-z₂).
Каждая координата произведения вектора на число равна произведению соответствующей координаты вектора на это число. Если k =
=  , то
, то  (kx₁; ky₁; kz₁).
(kx₁; ky₁; kz₁).
Координаты любой точки D в прямоугольной системе координат Оxyz равны соответствующим координатам вектора  .
.
Т.о. если A(x; y; z), то  (x ; y ; z).
(x ; y ; z).
Простейшие задачи в координатах.
Координаты середины отрезка.
| 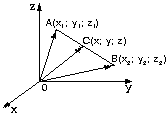
рис. 3
| 
Таким образом, каждая координата середины отрезка равна полусумме соответствующих координат его концов.
|
Вычисление длины вектора по его координатам.

Расстояние между двумя точками. M₁ (x₁; y₁; z), M₂(x₂; y₂; z₂), тогда

Косинус угла между векторами
Чтобы найти косинус угла между векторами нужно скалярное произведение этих векторов разделить на произведение их длин.
В случае, если векторы заданы на плоскости и имеют координаты  и
и  , то косинус между ними вычисляется по формуле:
, то косинус между ними вычисляется по формуле:
Если же векторы заданы в пространстве, то есть  и
и  , то косинус угла вычисляется по формуле
, то косинус угла вычисляется по формуле
Примеры вычисления косинуса угла между векторами
Пример
Задание. Найти косинус угла  между векторами
между векторами  и
и 
Решение. Так как векторы заданы на плоскости, воспользуемся формулой
Подставим координаты заданных векторов:
Ответ. 
Пример
Задание. Найти косинус угла между векторами  и
и  , заданных в пространстве.
, заданных в пространстве.
Решение. Для нахождения косинуса угла между заданными векторами, воспользуемся формулой
Подставляя координаты векторов  и
и  , получим
, получим
Ответ. 







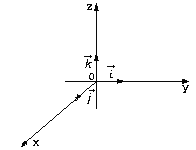
 +x₂; y₁+y₂; z₁+z₂); где
+x₂; y₁+y₂; z₁+z₂); где