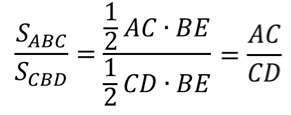Просмотр содержимого документа
«Опорный конспект по теме 'Площадь"»
Площадь – величина положительная.
Площадь квадрата равна квадрату его стороны.

![]()
а
Площадь прямоугольника. Площадь параллелограмма
 Площадь прямоугольника равна произведению его смежных сторон.
Площадь прямоугольника равна произведению его смежных сторон.
 А В
А В
SABCD = ab
a
C D
b
Основание - одна из сторон параллелограмма.
Высотой параллелограмма, проведённой к стороне, называется перпендикуляр, проведённый из любой точки противолежащей стороны к прямой, содержащей основание.
А В

![]()

![]() М
М
C D
Е
CD – основание
AE, АМ– высоты
Теорема. Площадь параллелограмма равна произведению его
основания на высоту.
SАВС = DС∙АЕ
Площадь трапеции
Высотой трапеции называется перпендикуляр, проведённый из любой точки одного из оснований на другое основание или его продолжение.

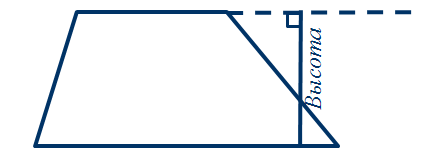
Теорема. Площадь трапеции равна произведению полусуммы длин её оснований на высоту.
Площадь трапеции равна произведению полусуммы длин её оснований на высоту.
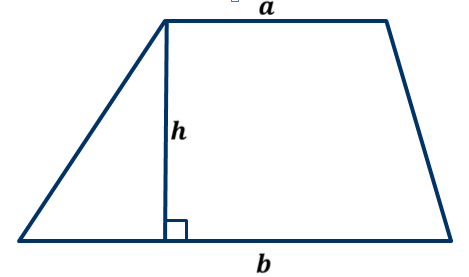
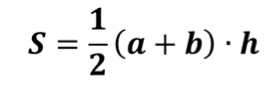
Площадь треугольника
Высотой треугольника называется перпендикуляр, проведённый из вершины треугольника на противоположную сторону или её продолжение.
Одну из сторон треугольника называют основанием. Под словом «высота» подразумевают высоту треугольника, проведенную к основанию.
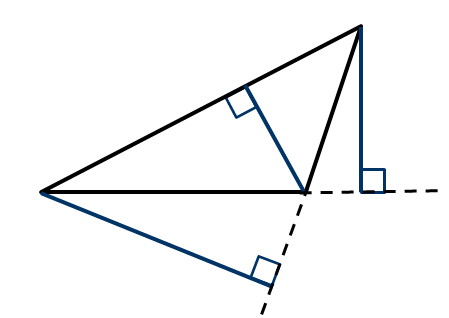
Основание - ВС, высота – АК
Основание – АС, высота - ВЕ
Основание – АВ, высота - СF
Теорема 1. Площадь треугольника равна половине произведения его основания на высоту.
![]()
 В
В
SАВС = 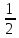 АС∙ВН
АС∙ВН
А С
Н
Следствия:
Площадь прямоугольного треугольника равна половине произведения длин его катетов.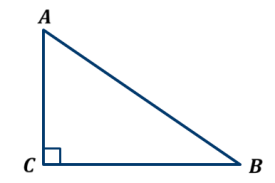
SАВС = 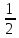 АС∙ВС
АС∙ВС
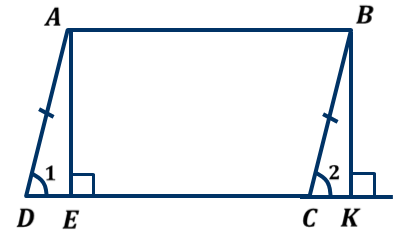
Если высота одного треугольника равна высоте другого треугольника, то их площади относятся как основания.
∆ АВС: АС – основание, ВЕ – высота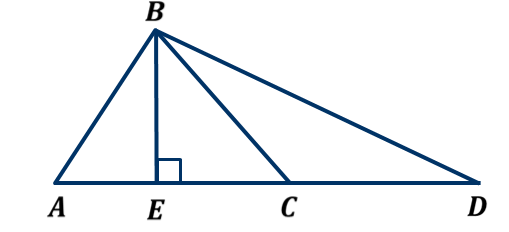
∆ CВD: CD – основание, ВЕ – высота
SАВС = 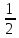 АС∙ВЕ; SCВD =
АС∙ВЕ; SCВD = 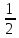 CD∙ВЕ
CD∙ВЕ
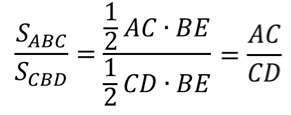
Теорема 2. Если угол одного треугольника равен углу другого треугольника, то площади этих треугольников относятся как произведения сторон, заключающих равные углы.
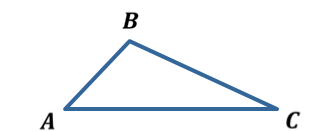
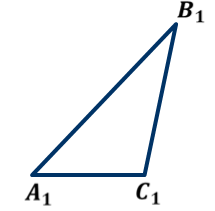
S
S1
![]() ∆ АВС
∆ АВС
![]() ∆ А1В1С1
∆ А1В1С1
∠А1=∠А2







 Площадь прямоугольника равна произведению его смежных сторон.
Площадь прямоугольника равна произведению его смежных сторон. А В
А В 






 В
В 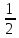 АС∙ВН
АС∙ВН