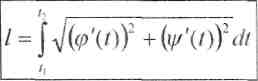Лекция №3
Тема: Определенный интеграл. Применение определенного интеграла к вычислениям площади плоских фигур, объемов тел.
Составление дифференциальных уравнений.
План:
-
Определение и свойства определенного интеграла. Формула Ньютона – Лейбница.
-
Вычисление определенных интегралов различными методами.
-
Применение определенного интеграла к вычислению площади плоской фигуры, объемов тел.
4. Ддифференциальные уравнения.
1.Определение и свойства определенного интеграла. Формула Ньютона – Лейбница.
Построение понятия определенного интеграла состоит из следующих этапов.
Пусть на отрезке [a, b] определена функция у = f(x). Отрезок [a, b] разобьем на п частей точками а = х0 1 2 п = b (разбиение R). На любом отрезке( 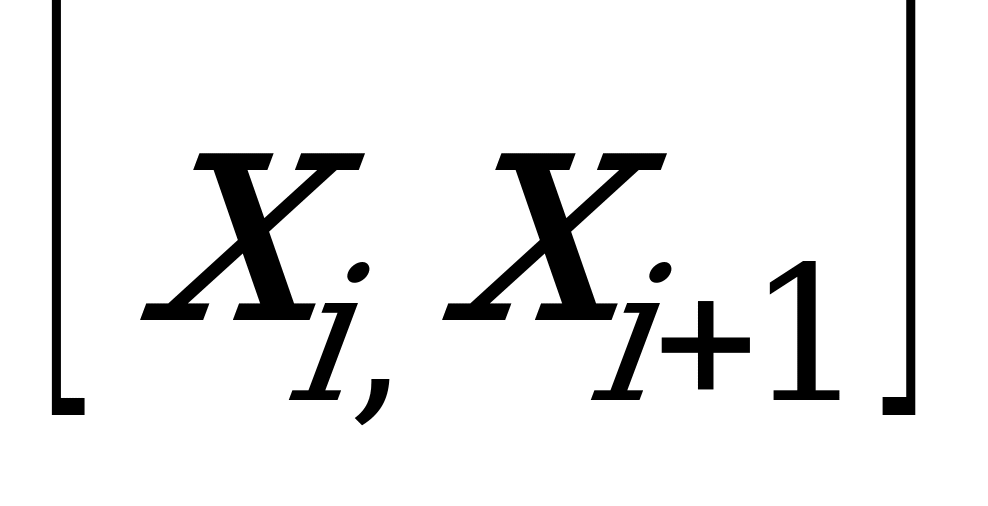 - частичный отрезок) выберем по произвольной точке ξ
- частичный отрезок) выберем по произвольной точке ξ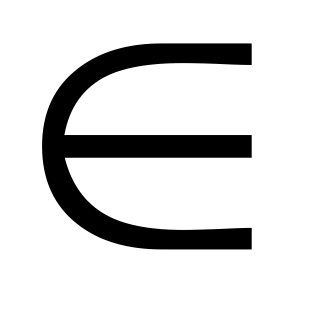 [х
[х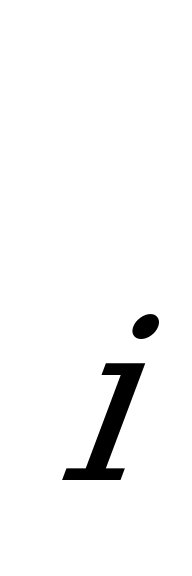 , xi+1]. (Рис1) ∆х
, xi+1]. (Рис1) ∆х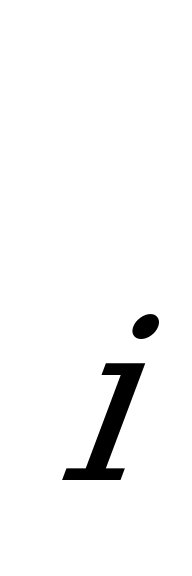 =х
=х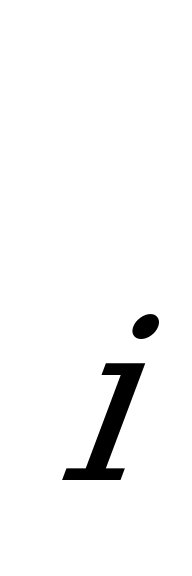 +1-х
+1-х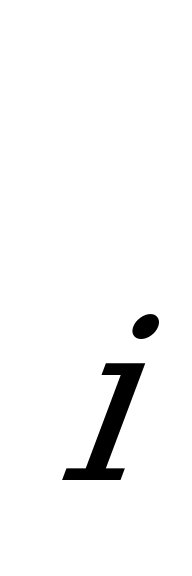 - длина отрезка. Составим сумму S
- длина отрезка. Составим сумму S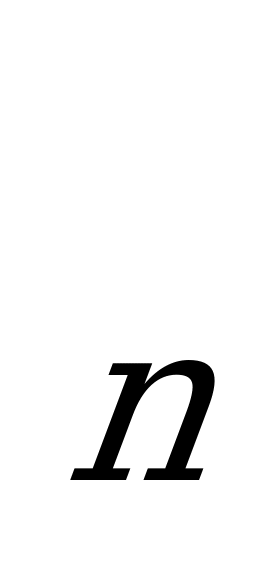 =
=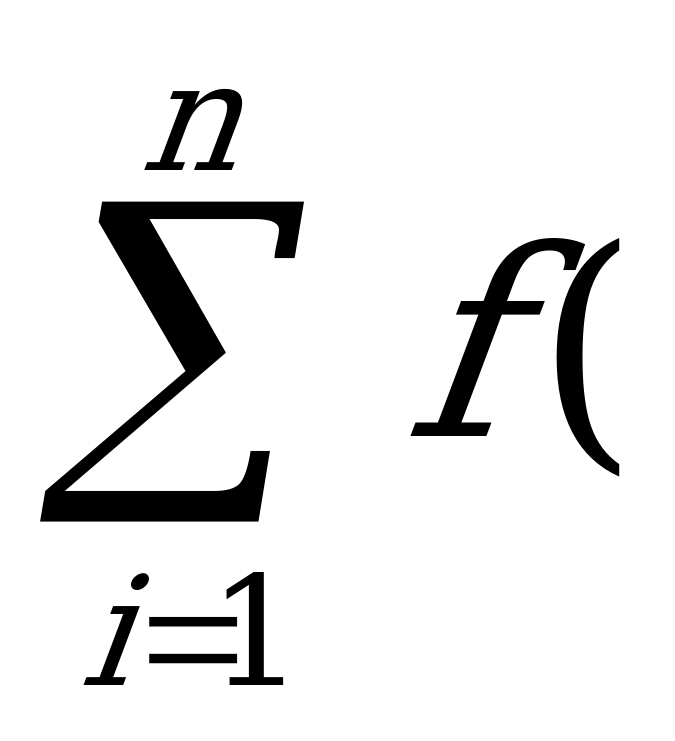 ξ
ξ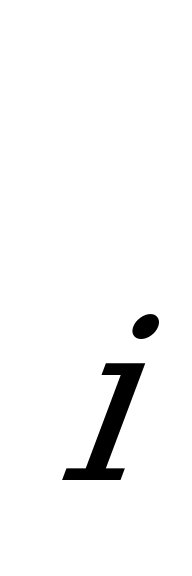 )∆х
)∆х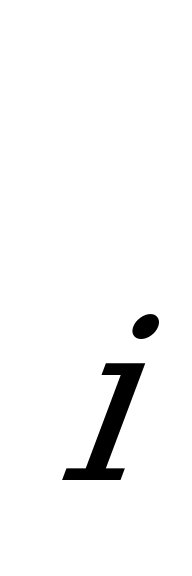 - n – ая интегральная сумма (Римана) функции f на отрезке [a, b].
- n – ая интегральная сумма (Римана) функции f на отрезке [a, b].
Г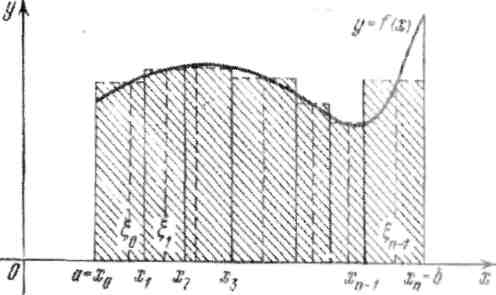 еометрический смысл суммы Sn - это есть алгебраическая сумма площадей
еометрический смысл суммы Sn - это есть алгебраическая сумма площадей
прямоугольников, в основании которых лежат отрезки ∆x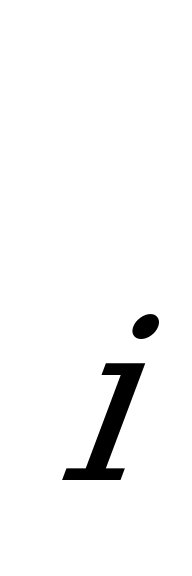 , a
, a
высоты равны f(ξ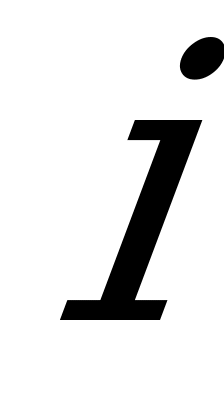 ). (В том
). (В том
случае функция неотрицательна функция)
Обозначим через γR = max ∆x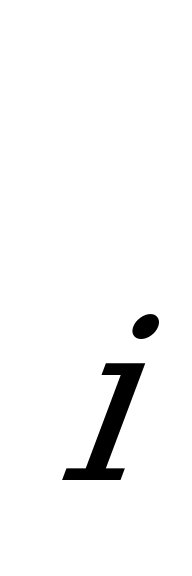 - максимальную длину отрезков
- максимальную длину отрезков
длину отрезков [х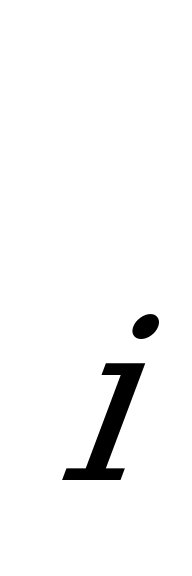 х
х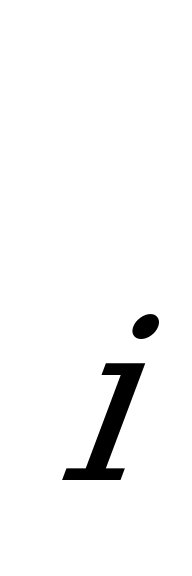 +1]
+1]
разбиения R. Предел (если он
существует), к которому
стремится интегральная сумма
рис1. Sn, когда γR = max ∆x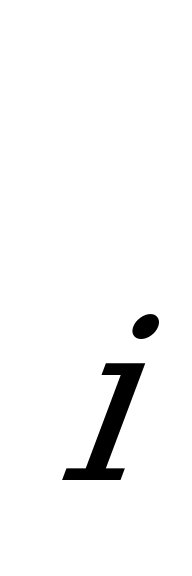 → 0, называется определенным интегралом от функции f на отрезке [a, b] и обозначается:
→ 0, называется определенным интегралом от функции f на отрезке [a, b] и обозначается:
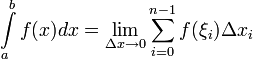
(1)
Предел (1) называют интегралом Римана и функцию, для которой этот предел существует называют интегрируемой в смысле Римана.
Определение: Определенным интегралом функции у=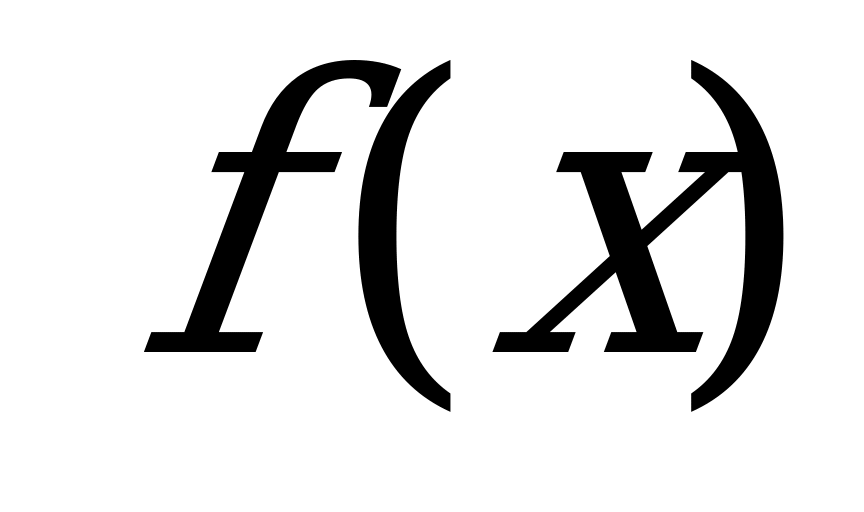 на отрезке
на отрезке 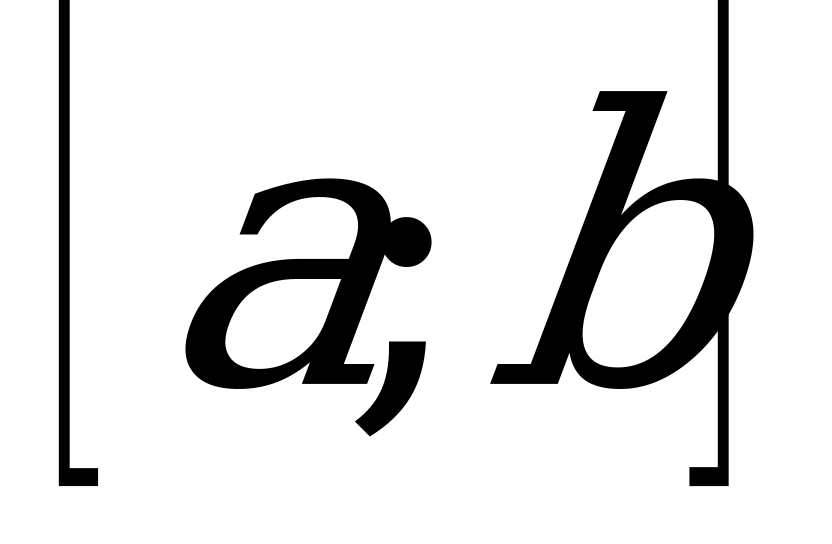 называется интеграл:
называется интеграл:
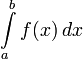
a – нижний предел.
b – верхний предел.
f(x) – подынтегральная функция.
dx- дифференциал независимой переменной.
Непосредственное вычисление определенного интеграла по формуле (1) связано с рядом трудностей, так как интегральные суммы имеют сложный вид, и найти их предел нелегко. До XVII века вычисление интегралов являлось трудной математической задачей. Ньютон и Лейбниц указали метод решения таких задач путем сведения к отысканию первообразной функции.
Таким образом, определенный интеграл вычисляется с помощью фундаментальной формулы Ньютона – Лейбница:
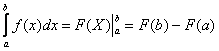
Определенный интеграл обладает рядом свойств, аналогичных свойствам неопределенного интеграла:
-
П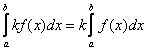 остоянный множитель можно выносить за знак интеграла :
остоянный множитель можно выносить за знак интеграла :
-
И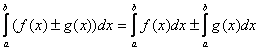 нтеграл от алгебраической суммы равен сумме интегралов от этих функций:
нтеграл от алгебраической суммы равен сумме интегралов от этих функций:
-
Для любых чисел a, b и с имеет место равенство:
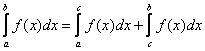
4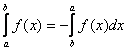 ) При перемене местами пределов интегрирования интеграл изменяет лишь знак:
) При перемене местами пределов интегрирования интеграл изменяет лишь знак:
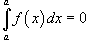
5)
2. Вычисление определенных интегралов различными методами.
-
Непосредственное интегрирование - вычисление интегралов с помощью непосредственного использования таблицы простейших интегралов, основных свойств неопределенных интегралов и формулы Ньютона – Лейбница.
-
Замена переменной в определенном интеграле:
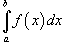
Определенный интеграл
по переменной x можно преобразовать в определенный интеграл относительно переменной t с помощью подстановки x = g (t):
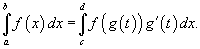
Новые пределы интегрирования по переменной t определяются выражениями
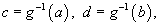
где g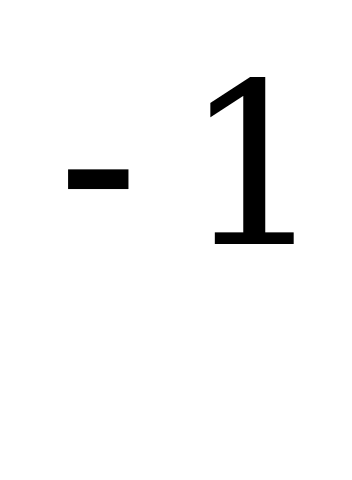 - обратная функция к g, т.е. t = g
- обратная функция к g, т.е. t = g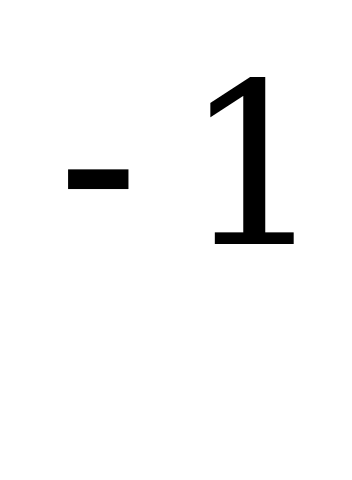 (x).
(x).
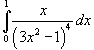
Пример1:
Решение.
Сделаем замену:
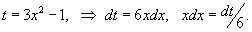
Пересчитаем пределы интегрирования. Если x = 0, то t = −1. Если же x = 1, то
t = 2. Тогда интеграл через новую переменную t легко вычисляется:
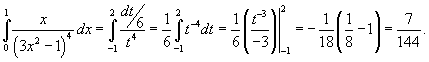
-
Интегрирование по частям для определенного интеграла
В этом случае формула интегрирования по частям имеет вид:
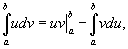
Г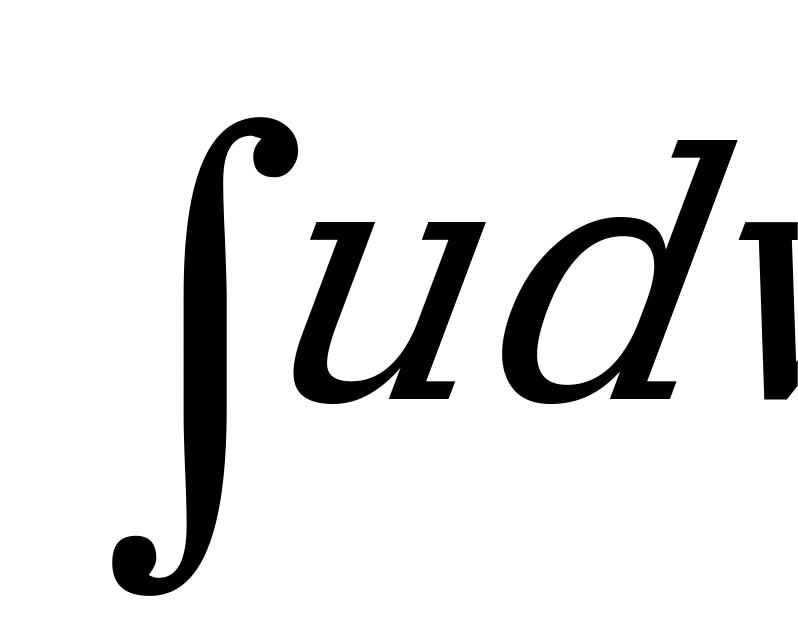
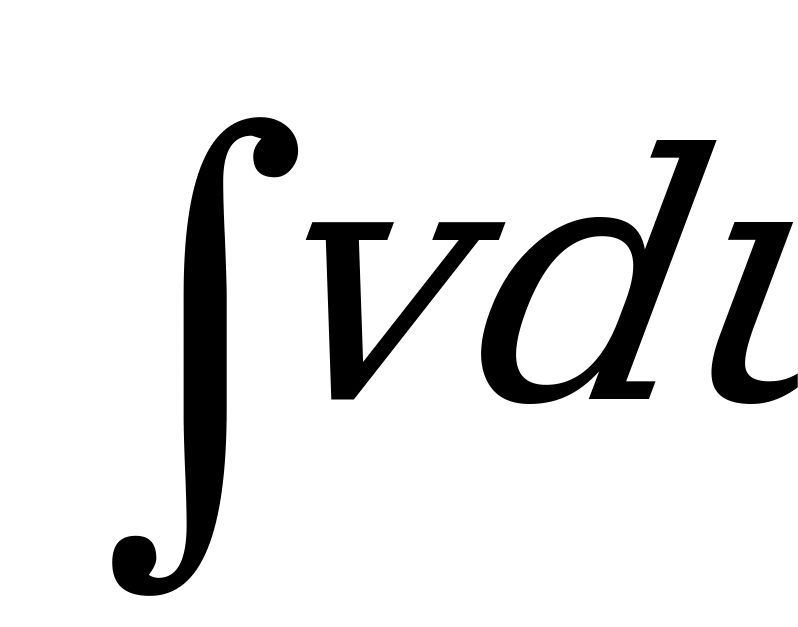 де u и v – непрерывно дифференцируемые функции от х. С помощью этой формулы нахождение интеграла сводится к отысканию другого интеграла
де u и v – непрерывно дифференцируемые функции от х. С помощью этой формулы нахождение интеграла сводится к отысканию другого интеграла
;
При этом за u берется такая функция, которая при дифференцировании упрощается, за dv – та часть подынтегрального выражения, интеграл от которой известен или может быть найден.
Пример 2:
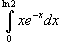
Вычислить интеграл
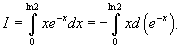
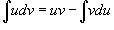 Используем интегрирование по частям: В нашем случае пусть будет
Используем интегрирование по частям: В нашем случае пусть будет
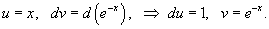
Следовательно, интеграл равен
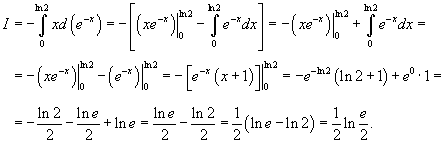
3. Применение определенного интеграла к вычислению площади плоской фигуры, объемов тел.
Фигура, ограниченная на плоскости ОХУ отрезком 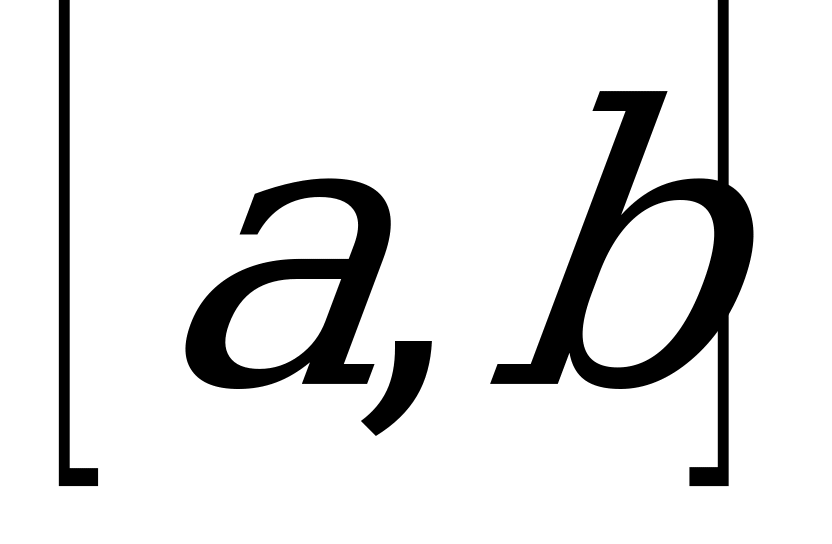 оси ОХ, прямыми х=a, x=b и графиком непрерывной и неотрицательной функции у = f(x) на [a,b], называется криволинейной трапецией.
оси ОХ, прямыми х=a, x=b и графиком непрерывной и неотрицательной функции у = f(x) на [a,b], называется криволинейной трапецией.
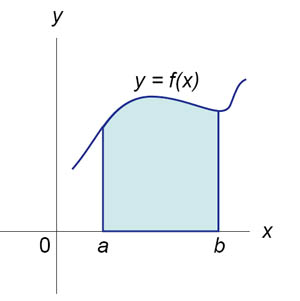
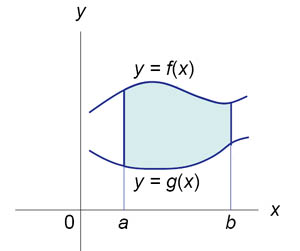
Площадь криволинейной трапеции вычисляется с помощью определенного интеграла:
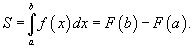
Пусть F (x) и G (x) - первообразные функций f (x) и g (x), соответственно. Если f (x) ≥ g (x) на замкнутом интервале [a, b],
то площадь области, ограниченной двумя кривыми y = f (x), y = g (x) и вертикальными линиями x = a, x = b (рисунок 2), определяется формулой
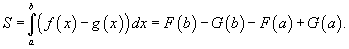
Вычисление объемов тел вращения:
Пусть дана кривая у=f(x), a≤x≤b. Объем тела вращения, ограниченного плоскостями х= a и х=b и поверхностью вращения кривой вокруг оси ОХ вычисляется по формуле:
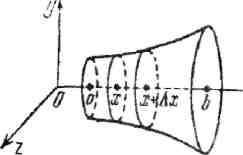
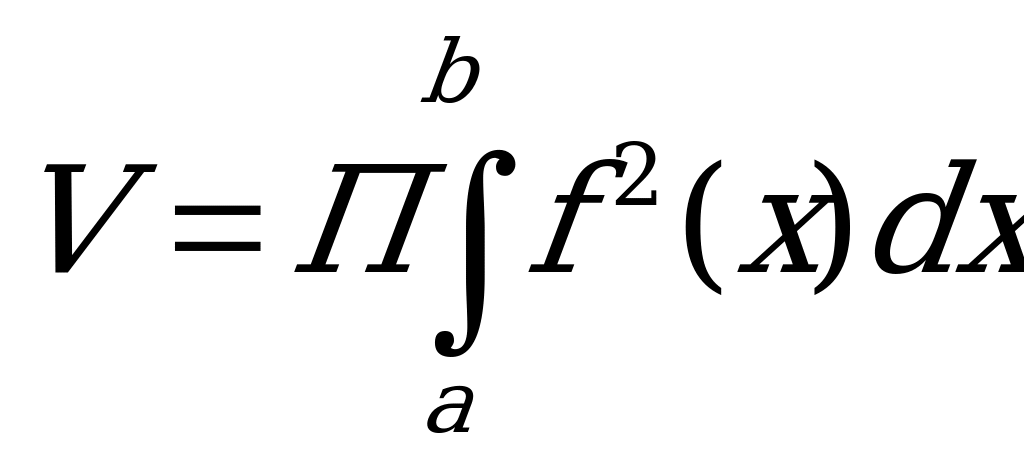
Аналогично можно получить формулу объема тела вращения вокруг оси ОУ
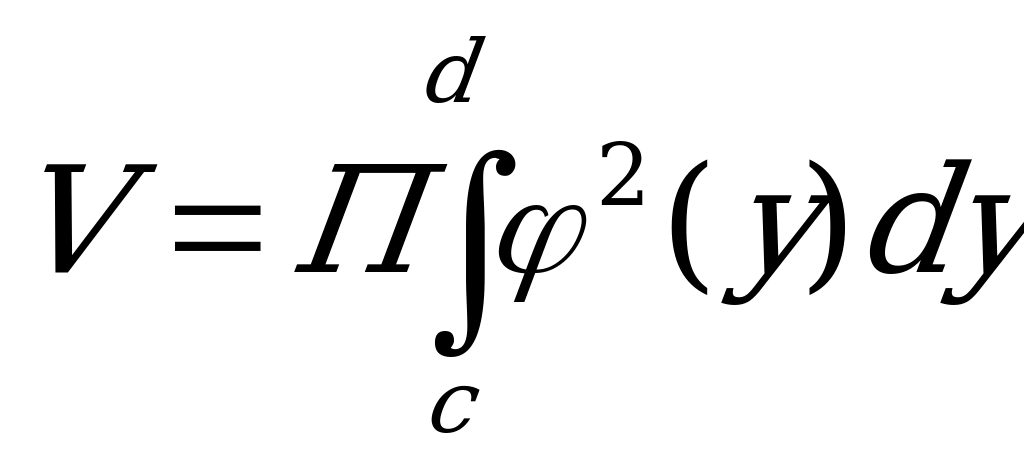 ;
;
Длина дуги кривой вычисляется по формуле:
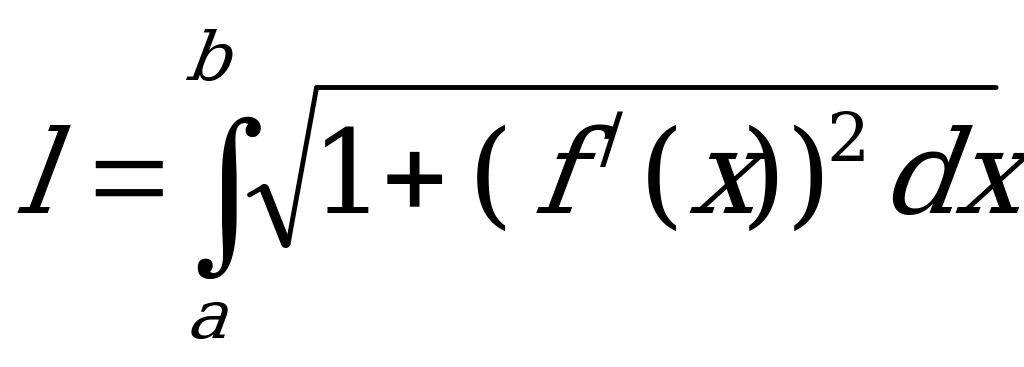
Если площадь сечения тела плоскостью, перпендикулярной оси Ох, выражена как функция от х, т.е. в виде Ѕ = Ѕ(х) (а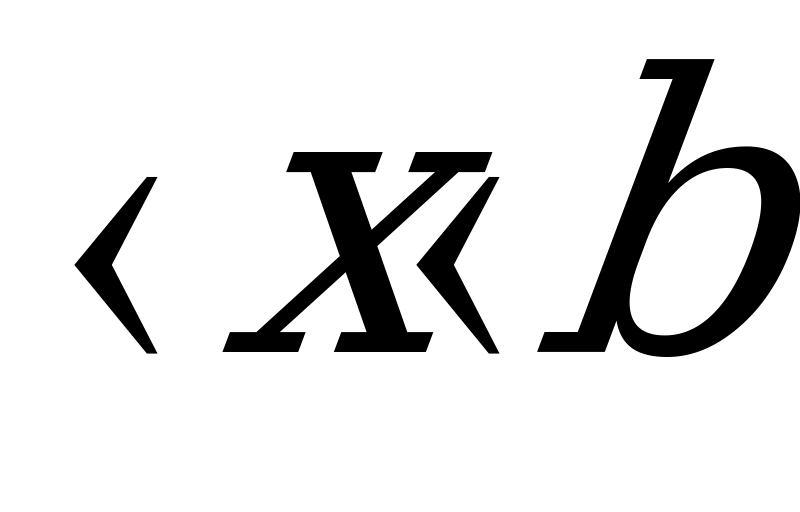 ), то объем части тела, заключенный между перпендикулярными оси Ох плоскостями х=а и х=b находится по формуле
), то объем части тела, заключенный между перпендикулярными оси Ох плоскостями х=а и х=b находится по формуле
V= 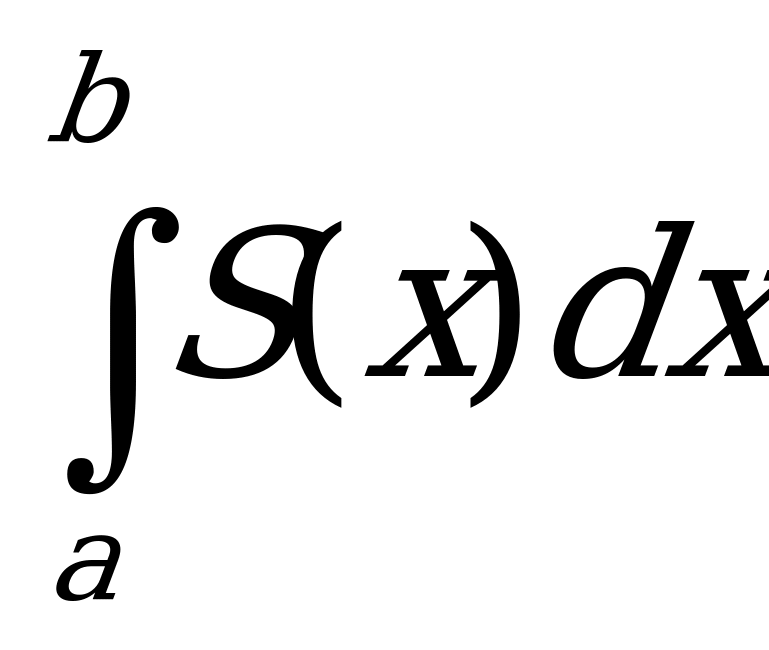
-
Дифференциальные уравнения:
Многие физические законы, которым подчиняются те или иные явления, происходящих в природе записываются в виде математического уравнения, выражающего определенную зависимость между какими-то величинами. Часто речь идет о соотношении между величинами, изменяющимися с течением времени. Соответствующее уравнение содержит одну или несколько функций и их производных. Большое значение, которое имеют дифференциальные уравнения для математики и особенно для ее приложений, объясняются тем, что к решению таких уравнений сводится исследование многих физических и технических задач. Дифференциальные уравнения играют существенную роль в других науках и областях, таких, как биология, экономика и электротехника. Дифференциальные уравнения широко применяются в области медицины: это волновые и колебательные движения, вязкость крови, для описания медико – биологических приложений ультразвука и т. д. В действительности, они возникают везде, где есть необходимость количественного(числового) описания явлений.
Дифференциальное уравнение - это уравнение, связывающее значение некоторой неизвестной функции в некоторой точке и значения её производных различных порядков в той же точке. Дифференциальное уравнение содержит в своей записи неизвестную функцию, ее производные и независимые переменны. Все дифференциальные уравнения можно разделить на обыкновенные дифференциальные уравнения(ОДУ), в которые входят только функции (и их производные) от одного аргумента, и уравнения с частными производными (УРЧП), в которых входящие функции зависят от многих переменных. Порядком или степенью дифференциального уравнения называется наибольший порядок производных, входящих в дифференциальное уравнение.
Первоначально дифференциальные уравнения возникли из задач механики, в которых участвовали координаты тел, их скорости и ускорения, рассматриваемые как функции времени. Формулировка второго закона Ньютона для материальной точки дает простейший пример обыкновенного дифференциального уравнения второго порядка с неизвестной функцией координат точки и временем, выступающим в роли независимой переменной.
О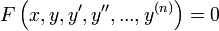
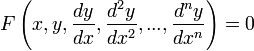 быкновенные дифференциальные уравнения (ОДУ) — это уравнения вида
быкновенные дифференциальные уравнения (ОДУ) — это уравнения вида
или
где 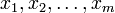 — неизвестная функция (возможно, вектор-функция; в таком случае часто говорят о системе дифференциальных уравнений), зависящая от независимой переменной x , штрих означает дифференцирование по x . Число n называется порядком дифференциального уравнения. Решением дифференциального уравнения называется раз дифференцируемая функция, удовлетворяющая уравнению во всех точках своей области определения. Обычно существует целое множество таких функций (такое параметризованное семейство рещений, называется общим решением дифференциального уравнения), и для выбора одного из них требуется наложить на него дополнительные условие: например, потребовать, чтобы решение принимало в данной точке данное значение. Полученное единственное решение называется частным решением.
— неизвестная функция (возможно, вектор-функция; в таком случае часто говорят о системе дифференциальных уравнений), зависящая от независимой переменной x , штрих означает дифференцирование по x . Число n называется порядком дифференциального уравнения. Решением дифференциального уравнения называется раз дифференцируемая функция, удовлетворяющая уравнению во всех точках своей области определения. Обычно существует целое множество таких функций (такое параметризованное семейство рещений, называется общим решением дифференциального уравнения), и для выбора одного из них требуется наложить на него дополнительные условие: например, потребовать, чтобы решение принимало в данной точке данное значение. Полученное единственное решение называется частным решением.
Дифференциальные уравнения с разделяющими переменными
П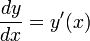 усть y(x) — некоторая функция, y'(x) — ее производная. Для удобства будем записывать
усть y(x) — некоторая функция, y'(x) — ее производная. Для удобства будем записывать
производную виде
имеющем смысл отношения бесконечно малых приращений — дифференциалов. Дифференциал dx — приращение значения переменной в окрестности x, стремящееся к нулю. Дифференциал функции dy — малое приращение функции, dy = f(x + dx) − f(x) = y'(x)dx. Пусть f(x) и g(y) — некоторые функции от x и y. Рассмотрим уравнение
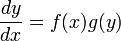
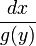 Уравнение такого вида называется обыкновенным дифференциальным уравнением с разделяющимися переменными. Умножим его на
Уравнение такого вида называется обыкновенным дифференциальным уравнением с разделяющимися переменными. Умножим его на
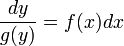 Последнее равенство означает, что малые приращения левой и правой частей равны. Поэтому их суммы также равны. Предположим что при x = x
Последнее равенство означает, что малые приращения левой и правой частей равны. Поэтому их суммы также равны. Предположим что при x = x y = y
y = y и возьмем интегралы от левой и правой частей. Пределы интегрирования — от y
и возьмем интегралы от левой и правой частей. Пределы интегрирования — от y до y для левой части и от x
до y для левой части и от x до x для правой части уравнения:
до x для правой части уравнения:
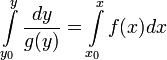
Р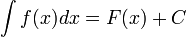 ешая получившееся в результате интегрирования алгебраическое уравнение, мы можем выразить y(x).Значения x
ешая получившееся в результате интегрирования алгебраическое уравнение, мы можем выразить y(x).Значения x и y
и y называются начальными условиями. В случае других начальных условий решение уравнения будет отличаться на постоянную. Поэтому, если начальные условия не даны, можно взять первообразные левой и правой частей и прибавить к ним константу. Используя неопределенный интеграл — обозначение множества первообразных -
называются начальными условиями. В случае других начальных условий решение уравнения будет отличаться на постоянную. Поэтому, если начальные условия не даны, можно взять первообразные левой и правой частей и прибавить к ним константу. Используя неопределенный интеграл — обозначение множества первообразных -
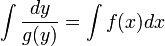 где F(x) — первообразная f(x), C — произвольная постоянная, запишем это в виде
где F(x) — первообразная f(x), C — произвольная постоянная, запишем это в виде
Следует отметить, что у дифференциального уравнения с разделяющимися переменными могут существовать так называемые нулевые решения — постоянные y, удовлетворяющие уравнению g(y) = 0. При них равны нулю как правая, так и левая части дифференциального уравнения (поскольку производная константы равна нулю).
Пример1:
Решить дифференциальное уравнение
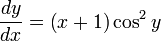
Разделим переменные:
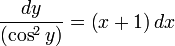
Т. к. начальные условия не заданы, возьмем неопределенный интеграл от обеих частей уравнения:
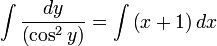
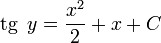
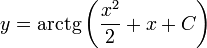
Осталось лишь выразить y через x:
Найдем также нулевые решения:
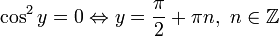
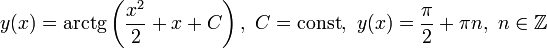
Ответ:
ff*W
Запишем параметрическое уравнение эллипса: x = acos/, y = bsmt. С учетом
а 0 ■ я/2
симметрии фигуры получаем S - 4 j ydx -A j a sin t(~b sin t)dt =4ab I sin2 tdt =
nil
. . t 1 -cos2/ , _ ,( 1
Aab J dt = 2ab\ t-
nab.
\ 2 Площадь в полярных координатах.
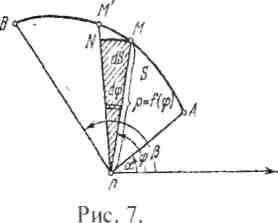
Задача. Найти площадь
S сектора ОАВ, ограниченной данной линией
р = f{q) и двумя лучами
(р -а, ср =
р (Рис. 7.) где
р и
(р- полярные
координаты.
Для решения задачи разобьем сектор ОАВ на секторы лучами а = (ра [ й •■„_, Элемент и-ного сектора можно приближенно считать круговым сектором, ограниченным окружностью радиуса Р, =/О?,) • Площадь такого сектора
1
ASj = — pt А(р). Чтобы получить общую площадь суммируем площади всех полученных
И 1 П 1 Р
секторов. S = ^AS, =-^р;А(р, щ_^*-\рЧ(р.
J-! *~ i-\ ^~
l-l 1-1 a
Т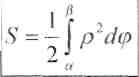 аким образом, получаем формулу для вычисления площади в полярных
аким образом, получаем формулу для вычисления площади в полярных
координатах:
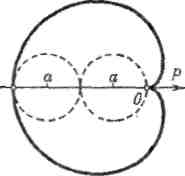
Пример 4. Вычислить площадь фигуры ограниченной кардиоидой
р = а(\ -coscp) (Рис. 8)
Учитывая симметрию фигуры можно записать
| 71 Л П
S = 2-—\p2d(p = J (a(l-cos (p)fd(p = a2\(j -2cos
2 (p]d~
0
+ cos
H
(Ъ 1
(p -zsin q
dcp
— (p -2sin
2cp
Рис. 8.
| ^' | \ |
| 2a | г-2аш^ |
| a | \ / |
| 0 | a 2a x |
|
| Рис. 9. |
S = 2• — \ 4а2 sin2 (pd
и2 \(\-cos7xp)dq =
т/4
2а2\ q sin2

Вычисление объемов тел вращения. Пусть Г есть кривая у = /(х), а Вычислим
У ю)
Производим разбиение отрезка [о, /] на части
а = х0 2 хп_, п = b
Считаем, что элемент объема AF тела ограниченного
объем тела вращения, ограниченного плоскостями х = а и х -Ь и поверхностью вращения кривой /"вокруг ОХ. (Рис.
Рис. 10.
плоскостями х = х; и х = хм приближенно равен объему цилиндра высоты Ах; = х;+| —xt, радиуса yt = /Ос,.). То есть AF = лу2Ах1 - itf (jc,)Ax..
Величина Ки = /Т^/2(х,)Аху приближенно выражает F и переходя к пределу
л-1 ''
имеем V - lim ^■V/2(xJ)Ax/ = n\ f2(x)dx. Мы получили формулу объема тела
п-1
1
max Дг, —0
вращения. Аналогично можно получить формулу объема тела вращения вокруг оси ОУ.
V = n\(p2(y)dy.
Пример 5. Вычислить объем тела, полученного вращением вокруг оси
Оу фигуры, лежащей в плоскости Оху и
о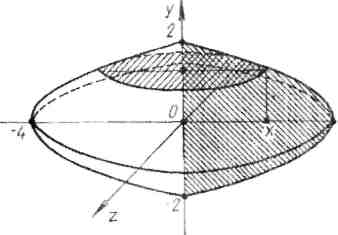 граниченной линиями у = 4 - х, х - 0 . Очевидно (Рис. 11), что
граниченной линиями у = 4 - х, х - 0 . Очевидно (Рис. 11), что
ь х
V}. = я j x2dy = п \ (4 - у2)1 dy =2тг| (4 - у2 )2 dy =
16-V+Z
3 5
2я\ (16- 8'2 + '4 )dy = 2л 512
( 64 32Л
л-«107,23
2л- 32 + —
Рис. 11.
15
I 3 5 J
Длина дуги кривой.
Определение. Под длиной дуги АВ понимается предел, к которому стремиться длина ломаной линии, вписанной в эту дугу, когда число звеньев ломанной возрастает неограниченно, а длина наибольшего звена ее стремиться к нулю.
| S/ | i |
|
|
|
|
|
|
|
|
|
| JhfU | Mi |
|
| W | \л | Mi | мн. | Щ | 4ft |
| ffb) |
|
| а |
|
|
| \ |
|
|
| i » |
| и |
| &х, | йхг | U- | —*»- | uxt | -*- -*•« | ix. | «* я |
Кривая называется гладкой, если она непрерывна и в каждой точке имеет касательную непрерывно меняющую свое положение от точки к точке.
Рассмотрим вопрос о длине дуги / кривой, заданной у = f(x), а b. Впишем
в данную гладкую кривую ломаную линию А = М0М1М2 •■•Мп_1Мп = В. (Рис. 12)
Проектируя точки А/, на Ох получим разбиение отрезка
[а, Ъ\ на п частей а = х0 2 л_, хн = Ь.
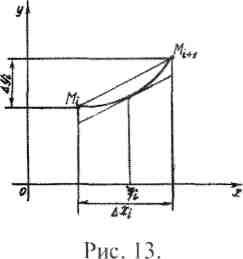
Рассмотрим /-тое звено ломаной [М,,А//+1]. (Рис. 13) Ду;-
приращение функции /(х) на Ах;.
А/, = М,ММ = ^Лх2+Ау2
Согласно теореме Лагранжа Ду; = Ах, • /'(§,) , £, е [хР х/+1].
Тогда А/, = М,Мм =л]\ +(/"'(£; ))2Ах; , а длину всей ломаной можно получить суммируя все ее звенья.
/ = ^-\/l + v (ь,)2)Ах, • Перейдем к пределу, считая, что наибольшее звено стремиться
к нулю.
/ = lim Хд/Пь (/'(£, )2 К -W =fVl+(/'W)2^
Пример 6. Найти длину дуги кривой у = — л/х между точками с абсциссами
х, = 3 и х2 = 8.
Согласно формуле имеем + xdx =
{l + Xf
3/2
38
3
Случай параметрически заданной кривой.
Гх = q{t)
Если линия задана в параметрическом виде, то есть t] t t2, где q(t)
[У = W(t)
и !//(/) непрерывно дифференцируемые на отрезке [/р^2] функции.
При стремлении длины отрезка ломаной к нулю можно считать, что А/, - dl, то
есть дифференциалу дуги. Тогда также Дх. - dx. Av — dy соответствующие
дифференциалы. Тогда можно записать A/, =MlMi+i = у Ах,2 + Ay,2 —»й?/ = д/ах2 + dy2 . Это формула для вычисления дифференциала дуги. Тогда / = J dl .
Так как dx = (p'(t)dt и dy = y/'(t)dt, то dl = yl((p'(t)dtf +(y/'(t)dtf = J(pVJf+(i//Xt))2dt и
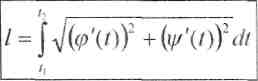
\x = a cos t
Пример 7. Найти длину дуги астроиды , . (Рис. 14.)
[у = asm" t
22
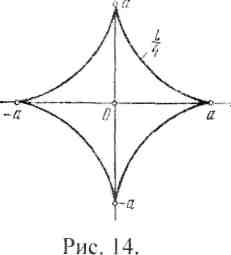
x'{t) = -За cos
2 /sin/. ''(/) = 3asin
2 /cos/
/
Ф
I v 9a2 cos4 / sin2 / + 9a2 sin4 / cos2 /J/ =
4 J
о
Л-/2 .т/2
= 3a J cos/ sin /J/ = 3a J sin td(sin /) =
nil
за
о sin2 /
= ia-
2
l = 6a
Длина дуги в полярных координатах.
Выведем сначала дифференциал dl дуги в полярных координатах. Из предыдущего раздела известно, что (dl)2 = (dx)" + (dy)2. где х н у— прямоугольные декартовы координаты точки дуги.
Как известно, формулы перехода от полярных координат р и ф к прямоугольным х и у следующие: х = pcoscp, у= р sin ср . Тогда dx = x'(p)dp - (р' cosp - ps'm(p)d(p dy = y\(p)d(p = (p' sinp + pcoscp)dp . Возведя в квадрат и складывая, получим (dl)" ={p'2 cos2 p -2p'pcospsinp + р2 sin2 2 sin2 ср + 2p'pcos(ps'm(p +
+ р2 cos2 (p){dq)2 = (p'2 + p2)(d
2
I—f2 Г
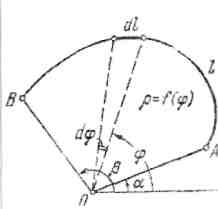
Следовательно, dl = ^p " + p'dq. (\)
Для того чтобы найти длину дуги непрерывно дифференцируемой кривой
р = р((р) между точками А и В (Рис. 15) необходимо проинтегрировать равенство (1) в пределах от р - а до р = р.
% Р ,
Рис.15. l = yp'2 + P2d(p
а
Пример 8.. Вычислить полную длину дуги кардиоиды (Рис. 8.) р = a(l -coscp). р' = as'mq)
Г / 7 7 ") * О С I " • 7
I = I -у/а (1 -cos
d(p = a\^jl-2cos(p + cos"(р + sin qd
=
= aj y2(l -cos
=aj -/2-2sin2 — dip =a\ 2sin — dcp ~ -4acos-
o о ' о
l~%a
Физические и механические приложения определенного интеграла.
4а
Одно из основных применений определенного интеграла - для вычисления работы переменной силы.
23
Задача. Найти работу А непрерывной переменной силы F(x), приложенной к материальной точке М, при перемещении последней вдоль оси Ох из положения х = а
в положение х = Ь, пред-
„--»—-*2?—«»^ М М F(x) полагая, что направление силы
" Л! ~~а ^ й совпадает с направлением пере-
мещения.
Пусть точка М переместилась
из положения х в положение х +
dx (Рис. 16.). На бесконечно
малом промежутке [х, х + dx]длины dx силу F(x) приближенно можно считать
постоянной. Поэтому элементарная работа силы равна
dA - F(x)dx
Интегрируя данное выражение в пределах отх=а до х=Ь, получим всю работу А = \F(x)dx
а
Кроме того, определенный интеграл применяется для вычисления некоторых механических величин, таких как: статистические моменты, моменты инерции и координаты центра масс.
Несобственный интеграл.
h
При определении интеграла J f{x)dx предполагалось, что 1) промежуток
а
интегрирования [a, b] конечен и 2) подынтегральная функция f(x)- определена и непрерывна на [а,Ь\. Иногда от одного (или обоих) этих предположений можно отказаться в этом случае интеграл имеет название несобственный интеграл.
I. Интеграл по бесконечному промежутку.
Определение. Пусть функция /(х) задана и непрерывна на полуинтервале
аТогда для любого х существует интеграл \ f(x)dx. Если существует
а В
предел lim \f(x)dx, то этот предел называют несобственным интегралом с
а
бесконечным верхним пределом интегрирования функции f(x) на интервале [а, + со] и записывают в виде
\f(x)dx- lim \f(x)d
При этом говорят, что интеграл сходится. В противном случае (предел не существует или равен со) говорят, что он расходится или не существует как несобственный интеграл.
24
Примеры.
+ в
1. [cosxdx = lim | cosxox = lim sini? -Предела нет. Несобственный интеграл не
существует.
2. 2х
» ■ в ,
.rax г ах
3. —г = lim —г = 1
im
= lim + 1
= 1 Интеграл сходится.
Утверждение: Если /(я;) 0, то интеграл | f(x)dx возрастает вместе с В.
а
Л"
Доказательство: Пусть В' В . так как j f{x)dx 0 (интеграл от положительной
функции), то J f(x)dx = j f(x)dx + J f(x)dx \f(x)dx
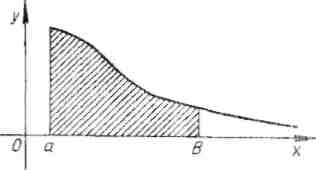
Известно, что всякая возрастающая переменная имеет предел (конечный или бесконечный), то есть при f{x) О интеграл
\ f(x)dx имеет (конечное или бесконечное
Рис. 17.
числовое значение. Геометрически - это площадь фигуры, ограниченной слева прямой
х = а, снизу осью Ох, сверху графиком y-f(x) и неограниченно простирающейся
направо. (Рис. 17.)
Пусть F(x) первообразная для /(х), тогда
+00 В
\f(x)dx = lim \f{x)dx- lim \F(B)- F(a)\. Если ввести обозначение
lim F(x) = F(+oo), то приходим к обобщенной формуле Ньютона-Лейбница
1-W
\f(x)dx=F(+°o)-F{a)
-roj
Мы подробно рассмотрели вычисление интеграла Г f(x)dx. Аналогично можно
определить интегралы с бесконечным нижним пределом и с обоими бесконечными пределами:
Глава 8.
ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
Определенный интеграл.
Определение 1. Пусть на отрезке [a, b] определена функция у = f(x). Отрезок [a, b] разобьем на п частей точками а = х0 1 2 п_{ п = b (разбиение R). На любом отрезке [x,,jc/+1] ([х,,хж] - частичный отрезок) выберем по произвольной точке Eiе[хп xi+l]. (Рис 1.) Дх, =х,+|-х, - длина отрезка. Составим сумму
п
Sn = V/(Ј,)AXj - п -ная интегральная сумма (Римана) функции / на отрезке [a, b].
Геометрический смысл суммы Sn- это есть алгебраическая сумма площадей

прямоугольников, в основании которых лежат отрезки Axj, a
высоты равны /(£,). (В том
случае если функция
неотрицательна.)
Обозначим через XR - max Ax, - максимальную
(iin-\
длину отрезков \хп х;+1]
разбиения R. Предел (если он
существует), к которому
стремится интегральная сумма
рис_ 1 _ Sn, когда XR - 0, называется
определенным интегралом от функции / на отрезке [a, b] и обозначается как
WmS„= lim Yf(i)Ax: = \f(X)dx(Y)
5 . П max A*; ~V ^^
ar ""* u i = I a
a, b- нижний и верхний пределы интегрирования, [а, Ь\- отрезок
интегрирования.
Предел (1) называют интегралом Римана и функцию, для которой этот предел существует называют интегрируемой в смысле Римана.
Данное определение эквивалентно следующему.
Определение Г. Определенным интегралом от функции f на отрезке [a,b] называется число I, удовлетворяющее следующему свойству: для всякого е 0 можно найти число 5 0 такое, что для любого разбиения R отрезка [а, Ь\, у которого XR = max Дх, 8 , выполняется неравенство
\S„ -1
Ј/(Ј)Ax;-7
при произвольном выборе точек £. е [хр х.+1].
В случае непрерывных функций понятие определенного интеграла введено Коши. Говорят, что непрерывная на [a, b] функция интегрируема в смысле Коши.
27
| i | X, | У, |
| 0 | 0,0 | 0,5000* |
| 1 | 0,1 | 1,0050 |
| 2 | 0,2 | 1,0198 |
| 3 | 0,3 | 1,0440 |
| 4 | 0,4 | 1,0770 |
| 5 | 0,5 | 1,1180 |
| 6 | 0,6 | 1,1662 |
| 7 | 0,7 | 1,2207 |
| 8 | 0,8 | 1,2806 |
| 9 | 0,9 | 1,3454 |
| 10 | 1,0 | 0,7071* |
Находим ^, = 11,4838. И по формуле трапеций имеем 7*1,148. Точное значение этого же интеграла, полученное по формуле Ньютона-Лейбница
+ -ln(l
■V2) «1,1479.
П Формула Симпсона
Более точную формулу можно получить, если профиль криволинейной полоски считать параболой, а не прямой линией как в формуле трапеций. В этом случае можно получить формулу Симпсона:
b ,
\f(x)dx*~--{f(a) + 2[f(a + 2h) + - + f(a + (n-2)h)]+
J Ъп
a
+ 4[f(a + h) + - + f(a + (n-l)h]+f(b)},h = — .
Пример 2. Вычислить приближенно |- —^dx
I.
y,=-
Промежуток интегрирования разбиваем на 10 частей (п = 10), h = 0,1. В таблицу запишем абсциссы точек деления х, и соответствующие им ординаты 1
| /' | х. | У, |
| 0 | 0,0 | 1,00000 |
| 1 | 0,1 | 0,99010 |
| 2 | 0,2 | 0,96153 |
| 3 | 0,3 | 0,91743 |
| 4 | 0,4 | 0,86206 |
| 5 | 0,5 | 0,80000 |
| 6 | 0,6 | 0,73529 |
| 7 | 0,7 | 0,67114 |
| 8 | 0,8 | 0,60975 |
| 9 | 0,9 | 0,55249 |
| 10 | 1,0 | О - ОС |
3






 еометрический смысл суммы Sn - это есть алгебраическая сумма площадей
еометрический смысл суммы Sn - это есть алгебраическая сумма площадей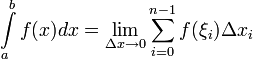
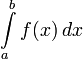
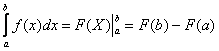
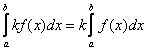 остоянный множитель можно выносить за знак интеграла :
остоянный множитель можно выносить за знак интеграла :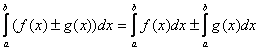 нтеграл от алгебраической суммы равен сумме интегралов от этих функций:
нтеграл от алгебраической суммы равен сумме интегралов от этих функций: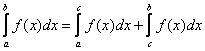
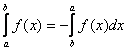 ) При перемене местами пределов интегрирования интеграл изменяет лишь знак:
) При перемене местами пределов интегрирования интеграл изменяет лишь знак: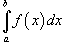
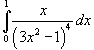
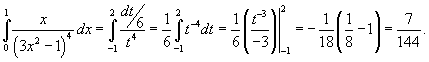
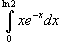
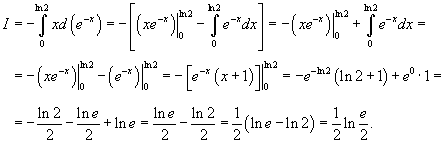



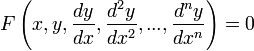 быкновенные дифференциальные уравнения (ОДУ) — это уравнения вида
быкновенные дифференциальные уравнения (ОДУ) — это уравнения вида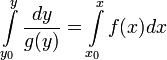


 граниченной линиями у = 4 - х, х - 0 . Очевидно (Рис. 11), что
граниченной линиями у = 4 - х, х - 0 . Очевидно (Рис. 11), что