Практическое занятие: Вычисление определенных интегралов
Сегодня мы научимся вычислять определенные интегралы. Прежде чем мы перейдем к практическим примерам, вспомним материал предыдущего урока и ответим на некоторые вопросы. Что такое определенный интеграл? В первую очередь – это число, в отличие от неопределенного интеграла, который является функцией. В общем виде определенный интеграл записывается так: 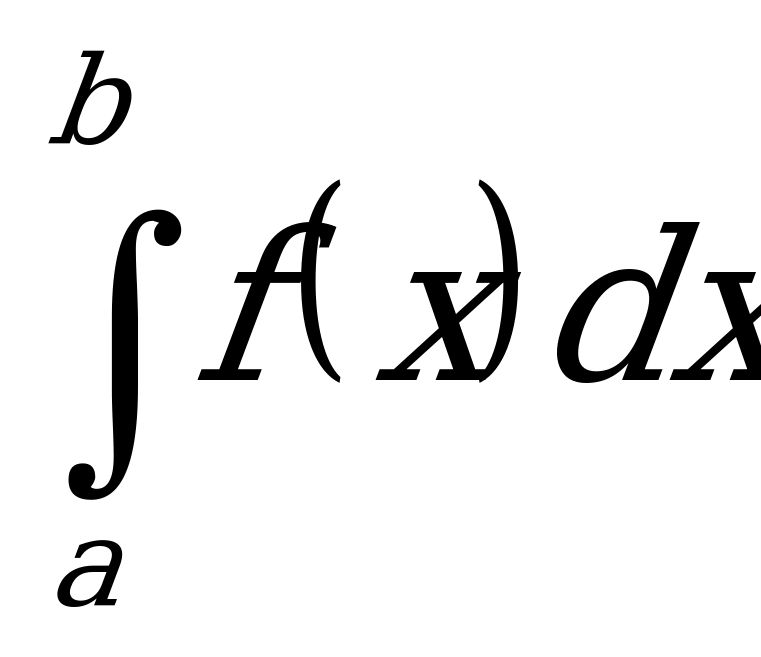 . Что прибавилось по сравнению с неопределенным интегралом? Прибавились пределы интегрирования. Что значит решить определенный интеграл? Решить определенный интеграл – это значит, найти число, заданное формулой
. Что прибавилось по сравнению с неопределенным интегралом? Прибавились пределы интегрирования. Что значит решить определенный интеграл? Решить определенный интеграл – это значит, найти число, заданное формулой 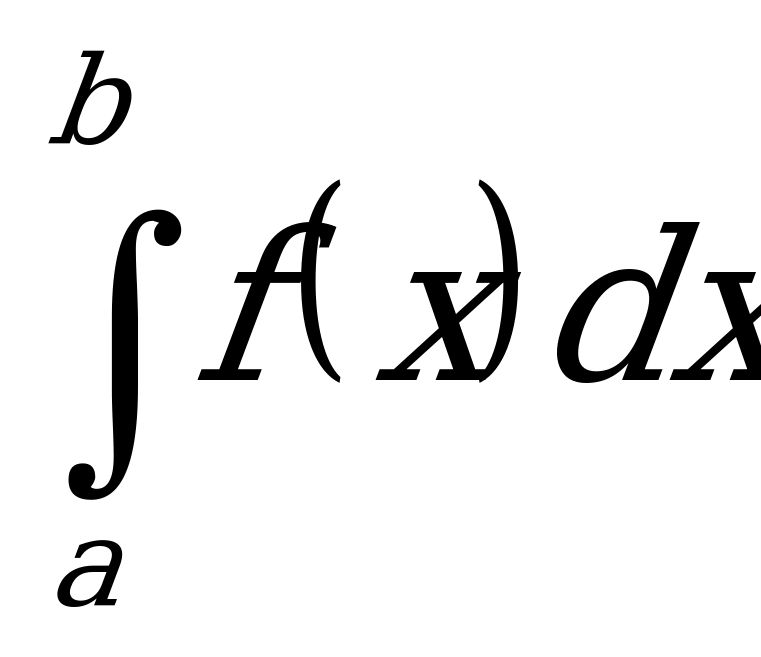 . Как его найти? С помощью формулы Ньютона-Лейбница:
. Как его найти? С помощью формулы Ньютона-Лейбница:
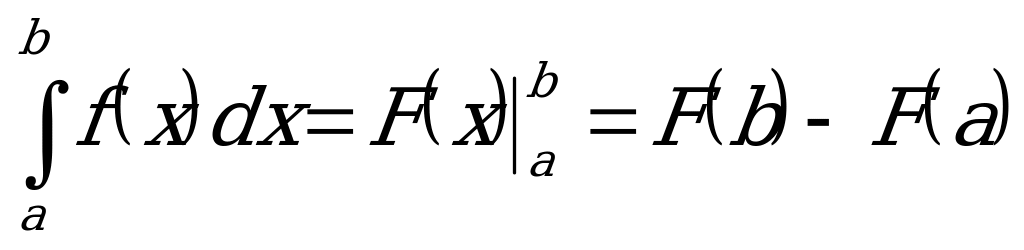 .
.
То есть, для того чтобы научиться решать определенные интегралы необходимо:
1) Уметь находить первообразные функций (неопределенные интегралы).
2) Уметь вычислить разность первообразных.
Как видите, для того чтобы освоить определенный интеграл, нужно достаточно хорошо ориентироваться в «обыкновенных» неопределенных интегралах. Для вычисления неопределенных интегралов мы использовали три метода интегрирования: метод непосредственного интегрирования, метод замены (введения новой переменной) и интегрирование по частям. Рассмотрим применение данных методов для вычисления определенных интегралов.
При этом, как и для неопределенного интеграла, для определенного интеграла справедливы свойства линейности:
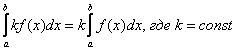
 – это справедливо не только для двух, но и для любого количества функций.
– это справедливо не только для двух, но и для любого количества функций.
Пример 1.Вычислить определенный интеграл

Решение:

(1) Используем свойства линейности определенного интеграла.
(2) Интегрируем по таблице, при этом все константы выносим – они не будут участвовать в подстановке верхнего и нижнего предела.
(3) Для каждого из трёх слагаемых применяем формулу Ньютона-Лейбница:
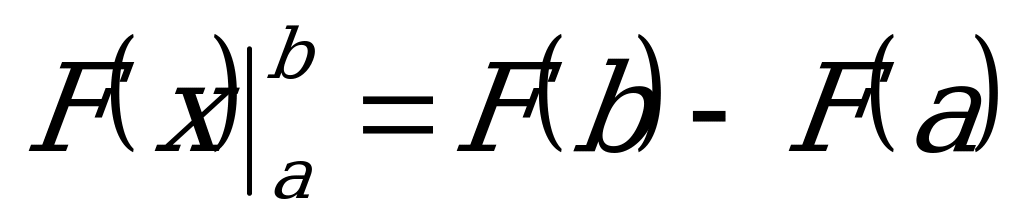
Решение обычно значительно сокращают и оформляют следующим образом:
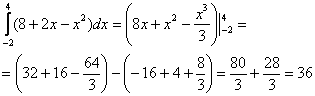
Ответ: 36.
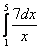
Пример 2. Вычислить определенный интеграл:
Решение:
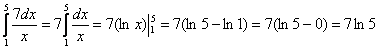
Ответ: 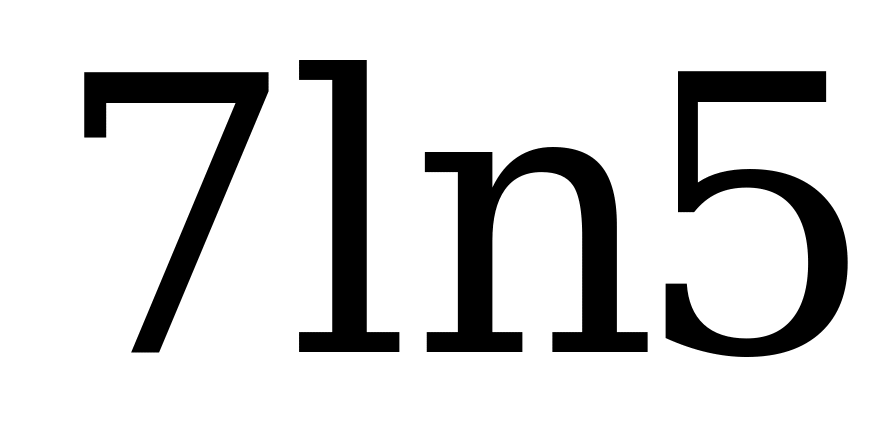 .
.

Пример 3: Вычислить определенный интеграл:
Решение:
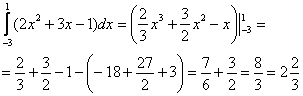
Ответ: 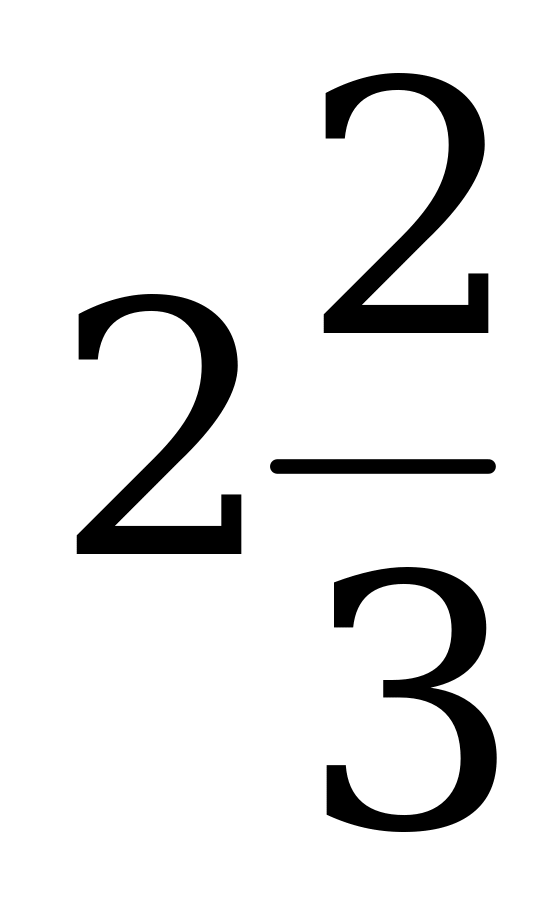 .
.
В определенном интеграле можно проводить замену переменной интегрирования. Для определенного интеграла справедливы все типы замен, что и для неопределенного интеграла.
Пример 4. Вычислить определенный интеграл:
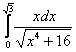
Решение:
Вводим новую переменную: 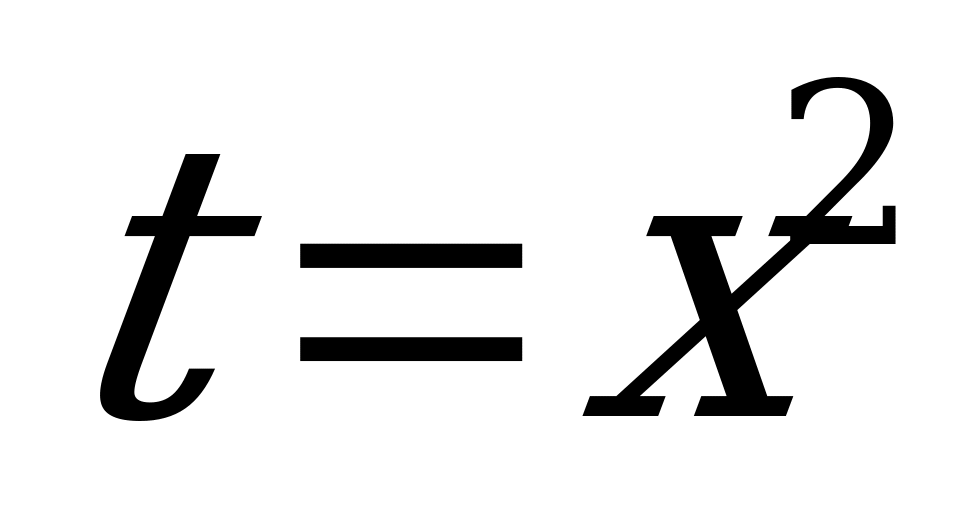 , тогда
, тогда 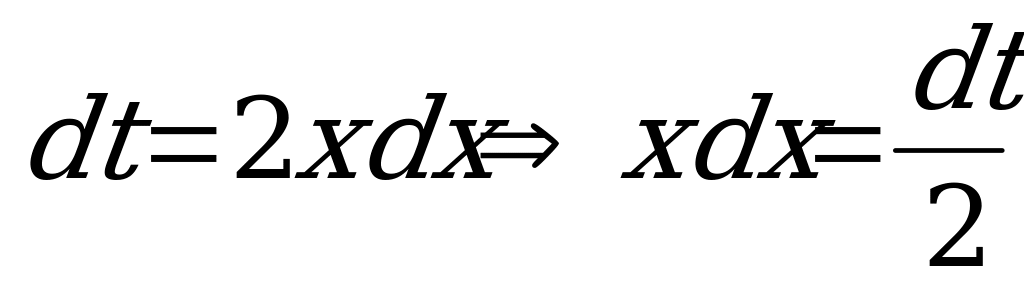 .
.
По сравнению с заменой в неопределенном интеграле у нас добавляется дополнительный этап: находим новые пределы интегрирования.
Это достаточно просто. Смотрим на нашу замену 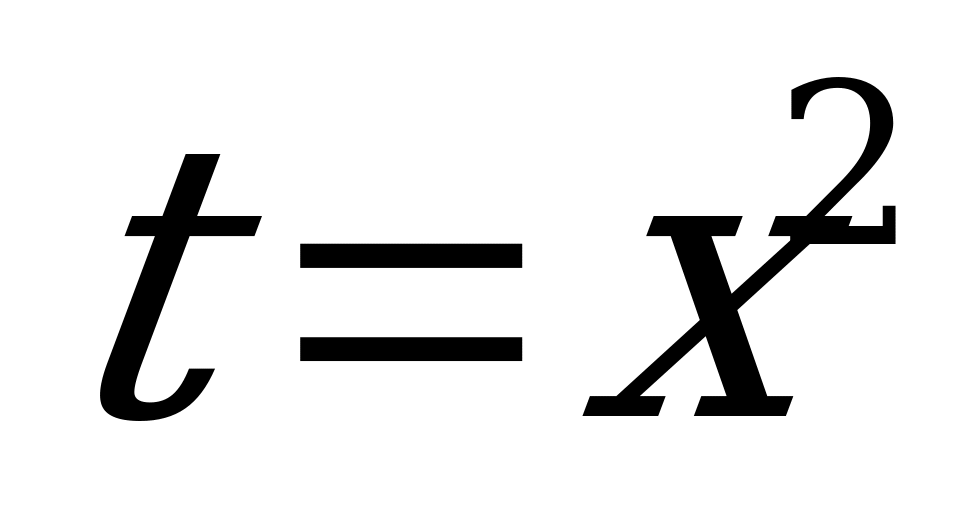 и старые пределы интегрирования
и старые пределы интегрирования 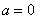 ,
, 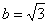 .
.
Сначала подставляем в выражение замены 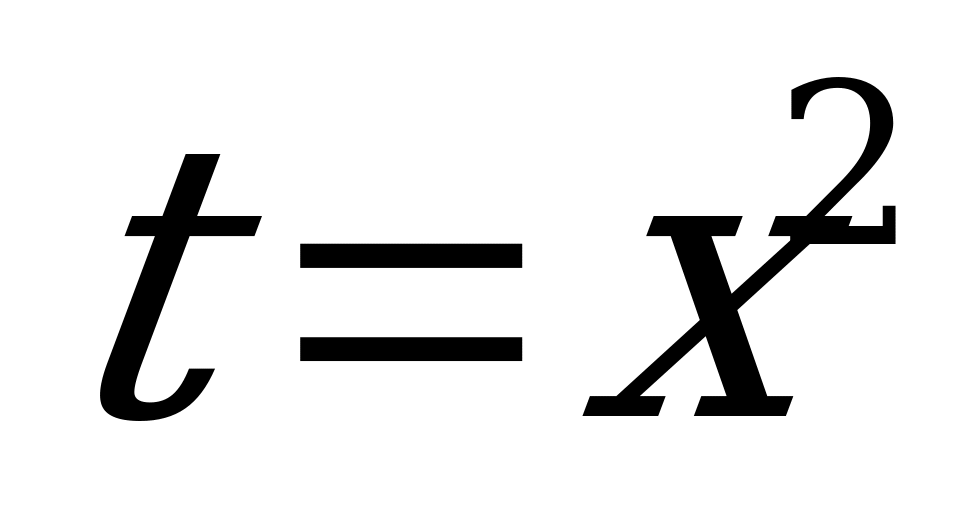 нижний предел интегрирования, то есть, ноль:
нижний предел интегрирования, то есть, ноль:
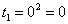
Потом подставляем в выражение замены 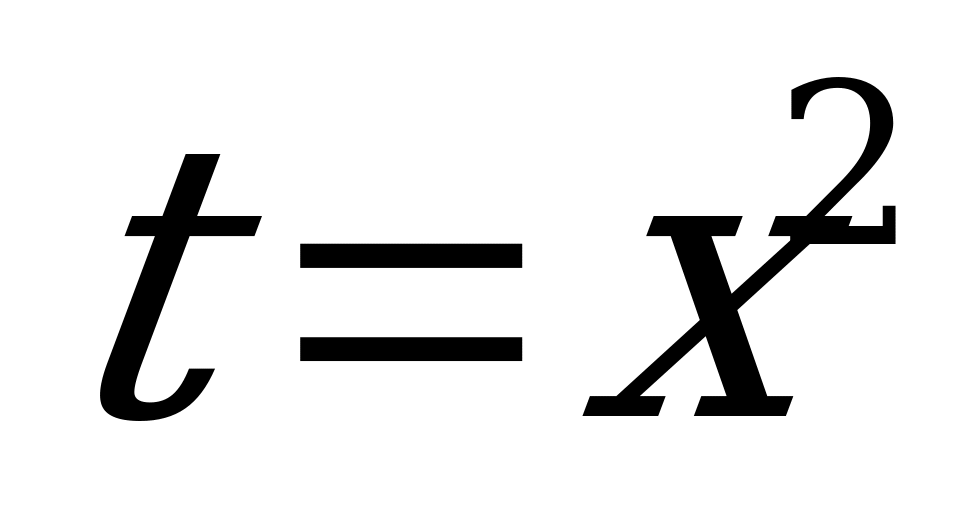 верхний предел интегрирования, то есть, корень из трёх:
верхний предел интегрирования, то есть, корень из трёх:
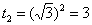
Продолжаем решение.

(1) В соответствии с заменой записываем новый интеграл с новыми пределами интегрирования.
(2) Это простейший табличный интеграл, интегрируем по таблице.
(3) Используем формулу Ньютона-Лейбница 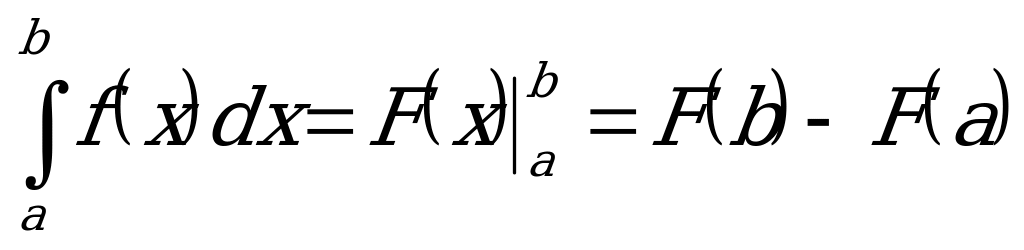 .
.
Ответ стремимся записать в максимально компактном виде, используем свойства логарифмов.
Ещё одно отличие от неопределенного интеграла состоит в том, что после того, как вычислили интеграл, обратную замену производить не надо.
Ответ: 0,35
Пример 5. Вычислить определенный интеграл:
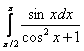
Решение:
Проведем замену переменной: 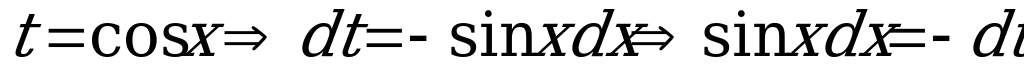 .
.
Найдем новые переделы интегрирования:
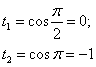
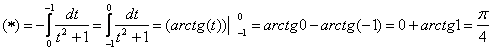
Ответ: 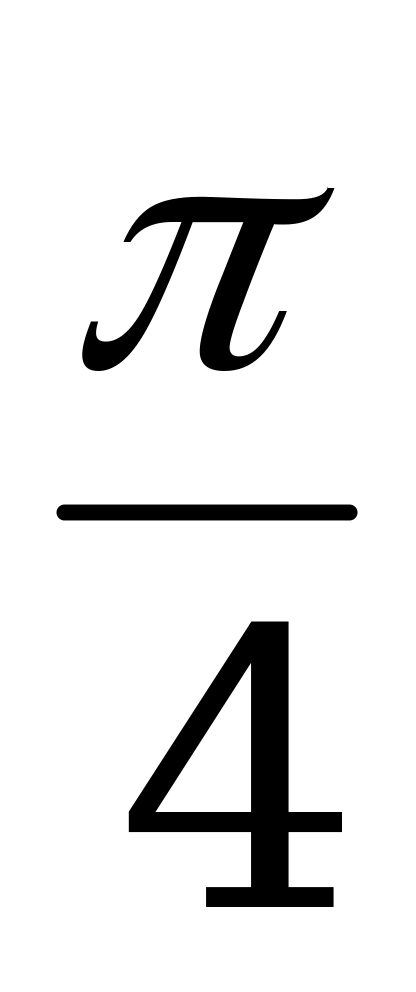 .
.
Пример 6. Вычислить определенный интеграл: 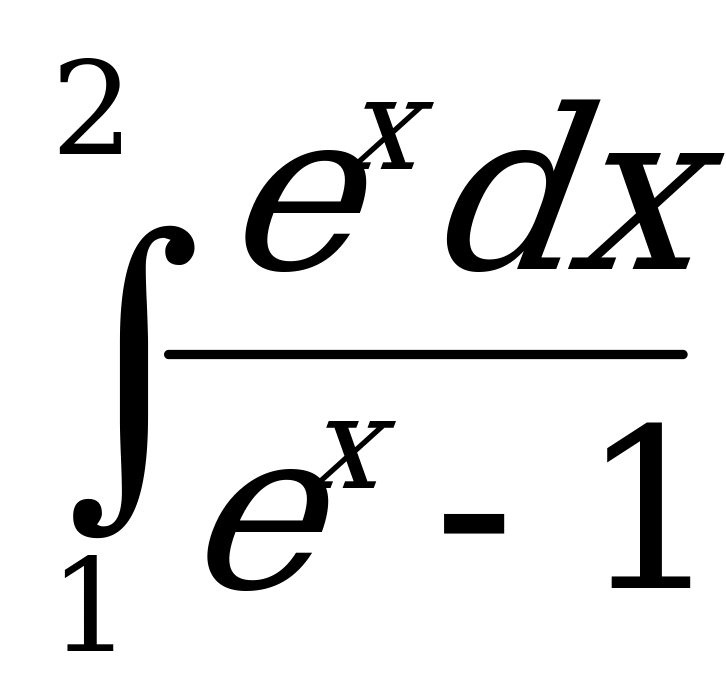
Решение:
Проведем замену переменной:  .
.
Найдем новые переделы интегрирования: 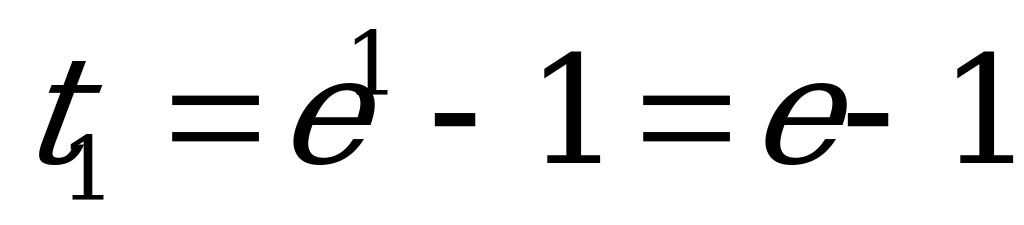 ;
; 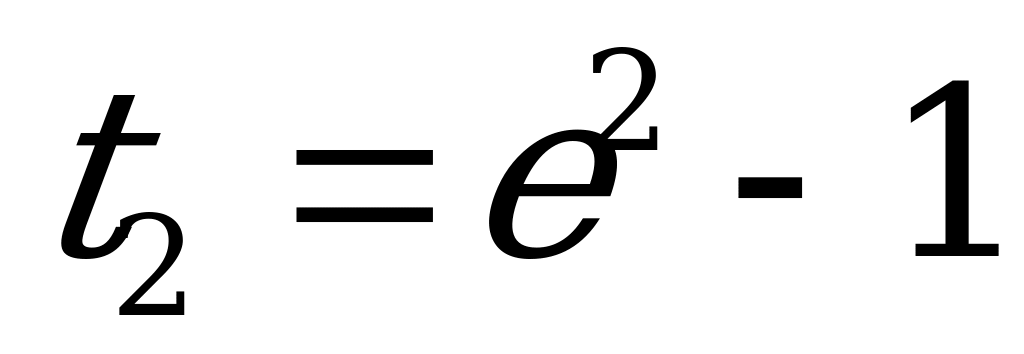 .
.
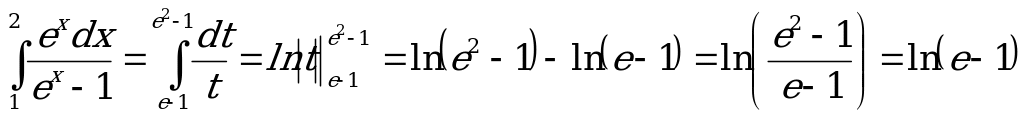 .
.
Ответ: 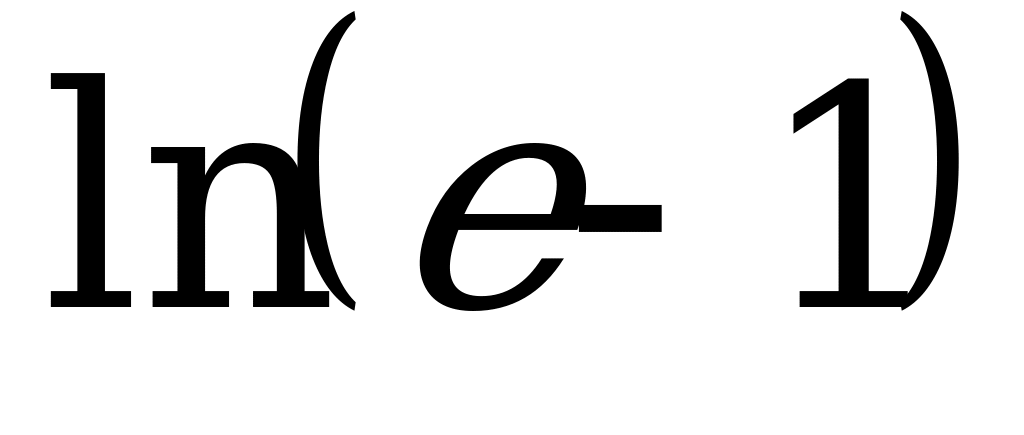 .
.
Для определенного интеграла справедлива формула интегрирования по частям, которая в данном случае будет иметь вид:
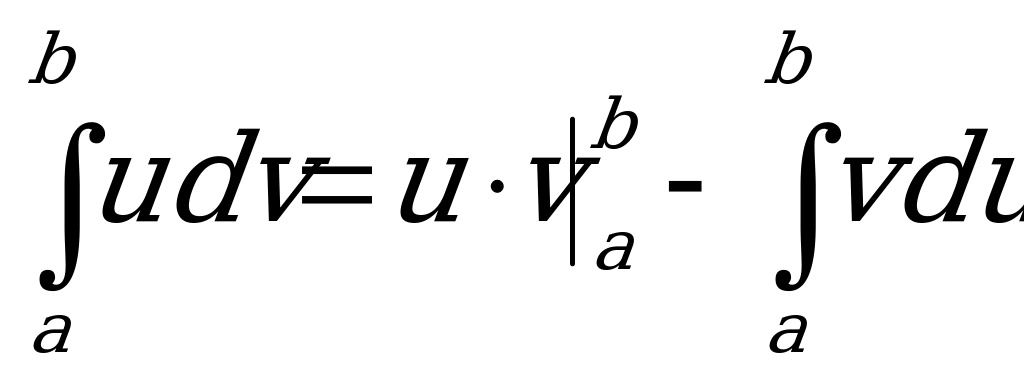 .
.
Пример 7. Вычислить интеграл 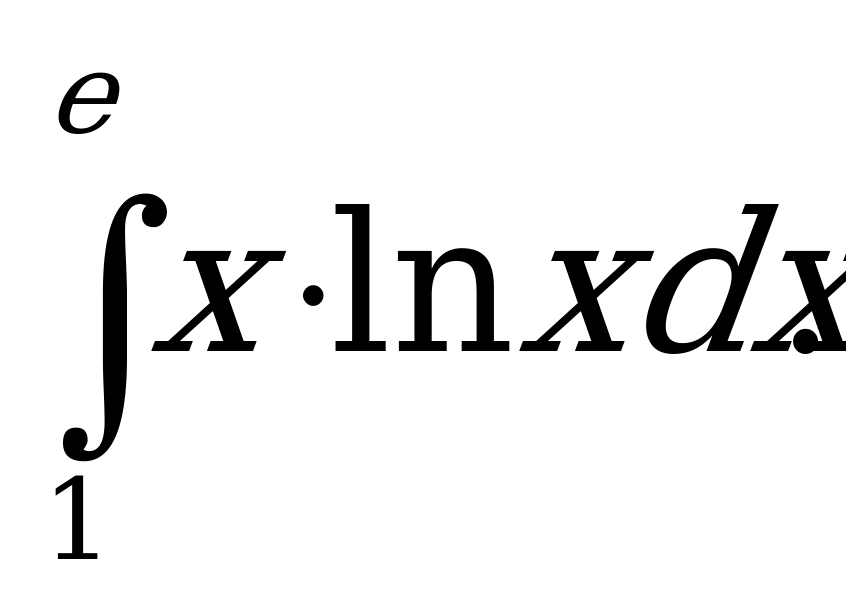
Решение:
Данный интеграл находим при помощи метода интегрирования по частям.
Затем в полученное выражение подставим соответствующее значение аргумента х.
Пусть 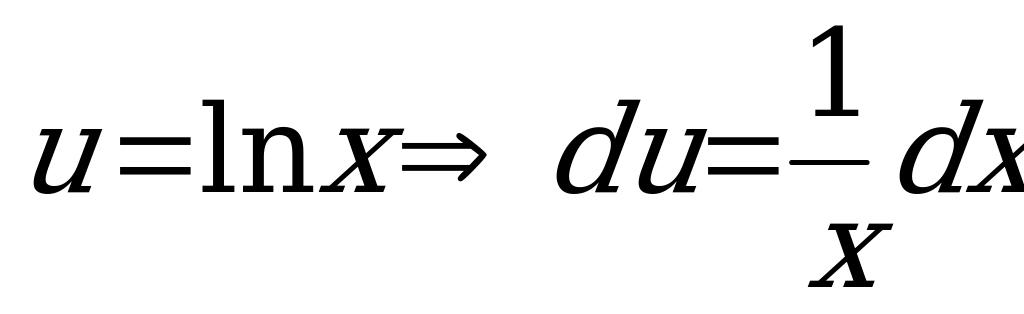
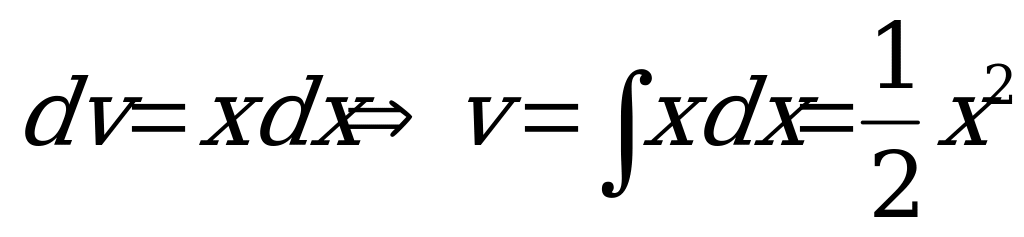 , тогда имеем:
, тогда имеем:
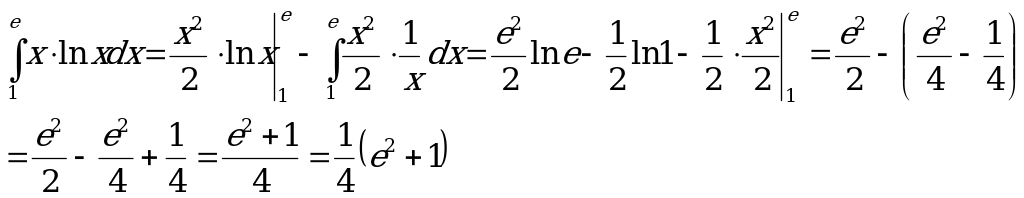
Ответ: 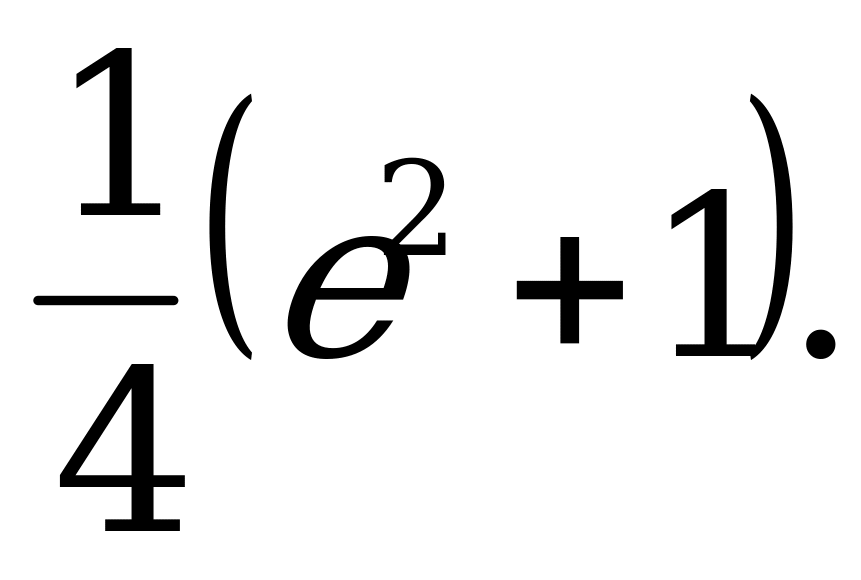
Самостоятельная работа
Вычислите определенные интегралы:
1) 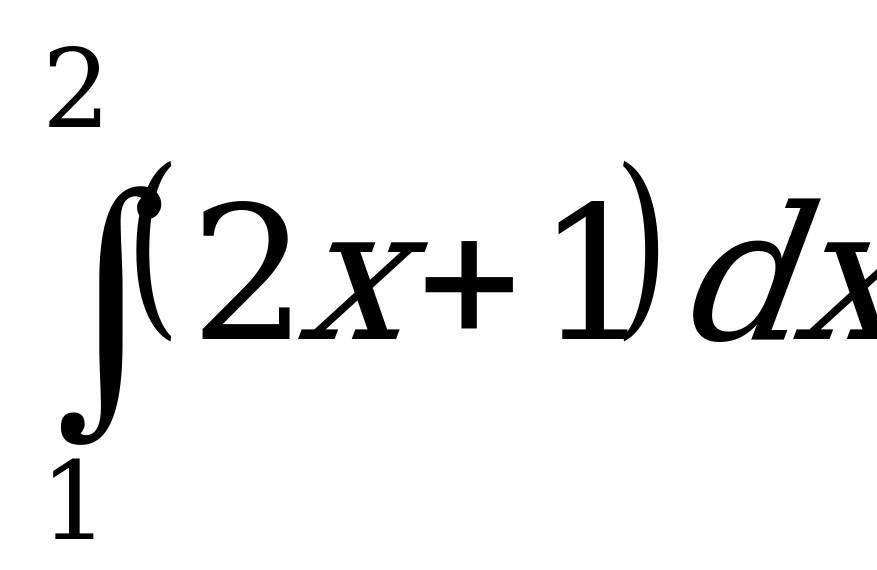 ;
;
2) 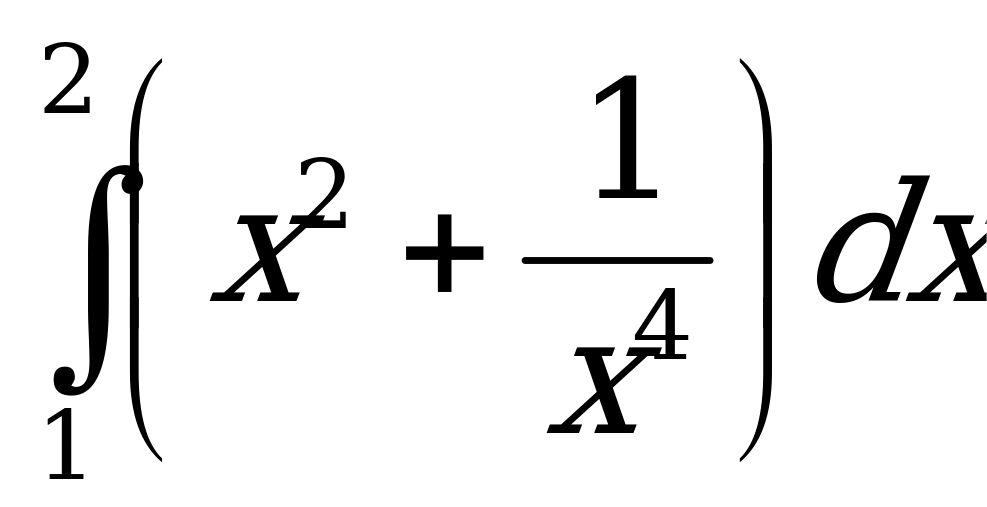 ;
;
3) 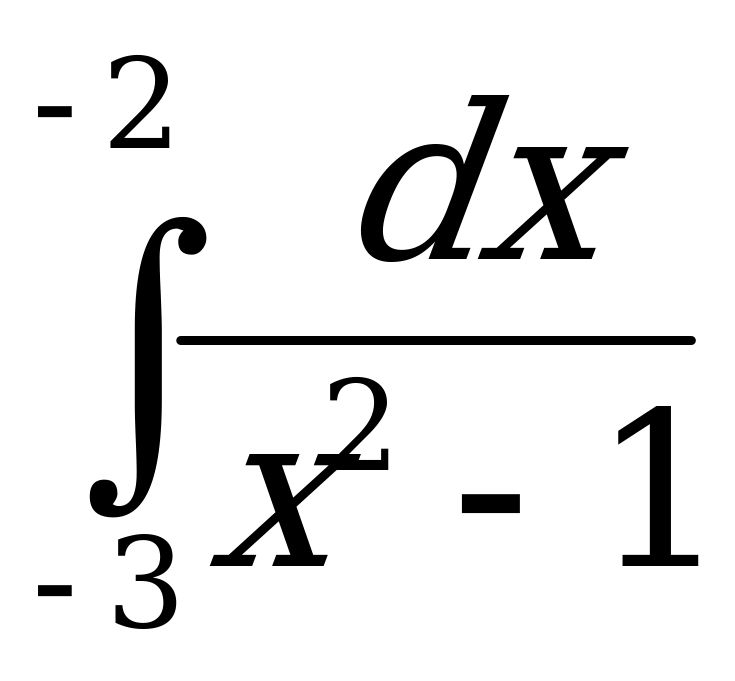 ;
;
4) 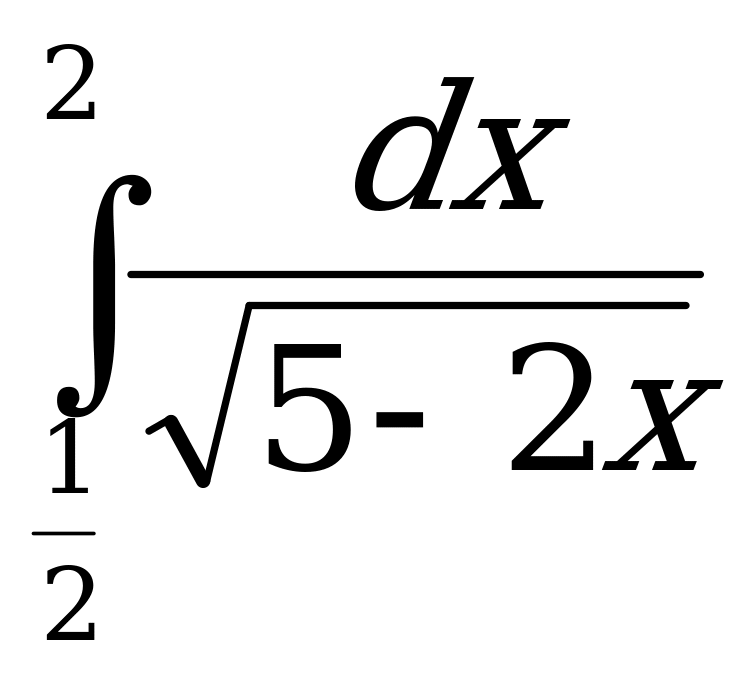 ;
;
5) 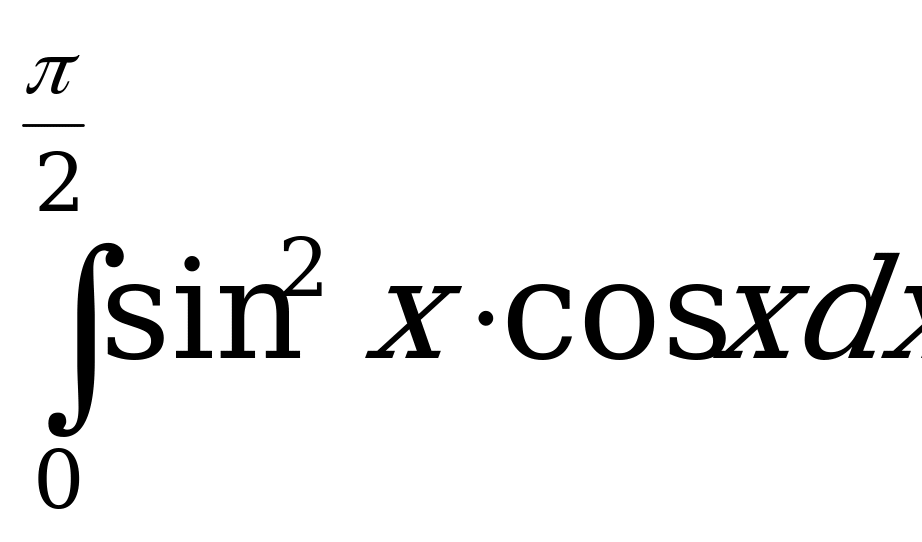 ;
;
6) 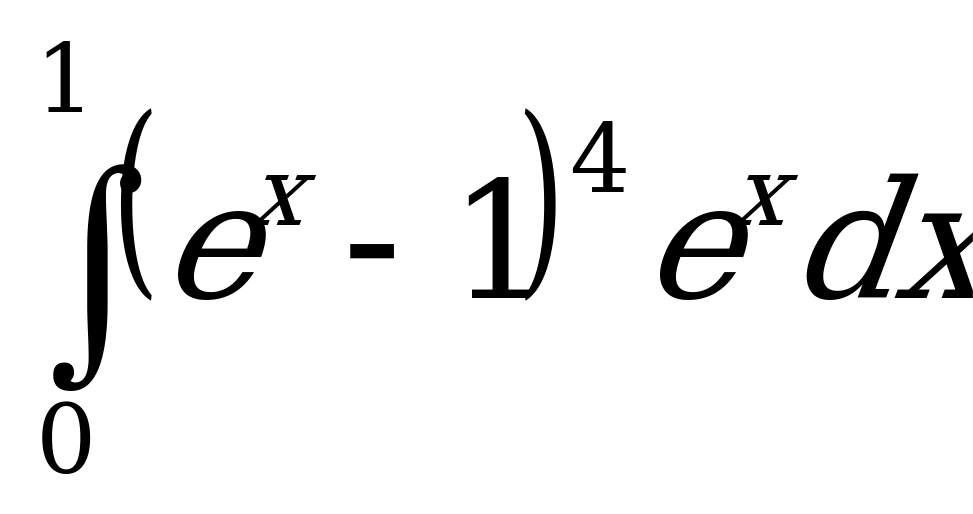 .
.
5





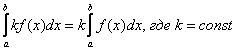
 – это справедливо не только для двух, но и для любого количества функций.
– это справедливо не только для двух, но и для любого количества функций.
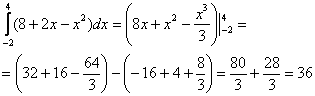

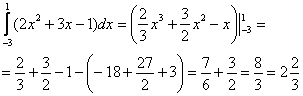
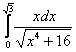

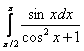
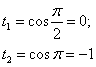
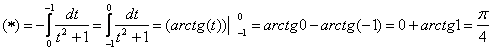
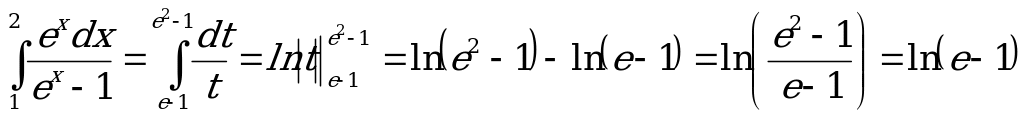 .
.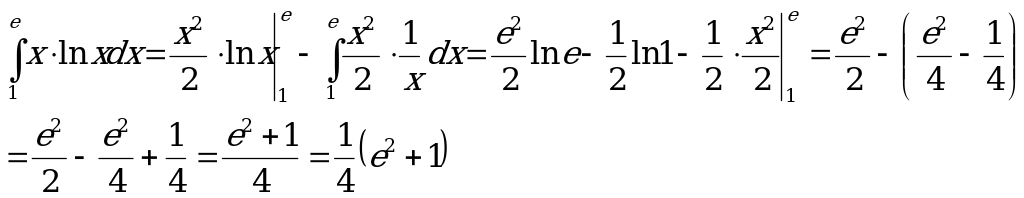
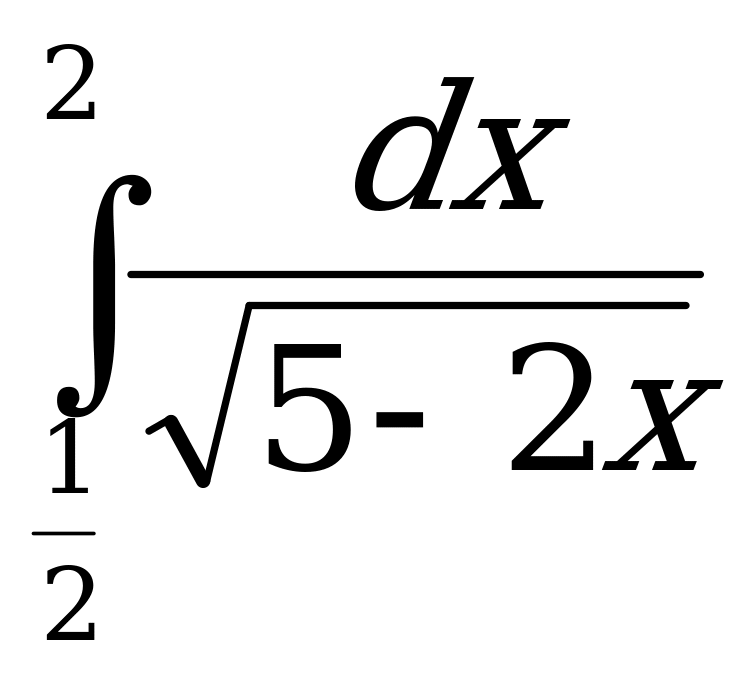 ;
;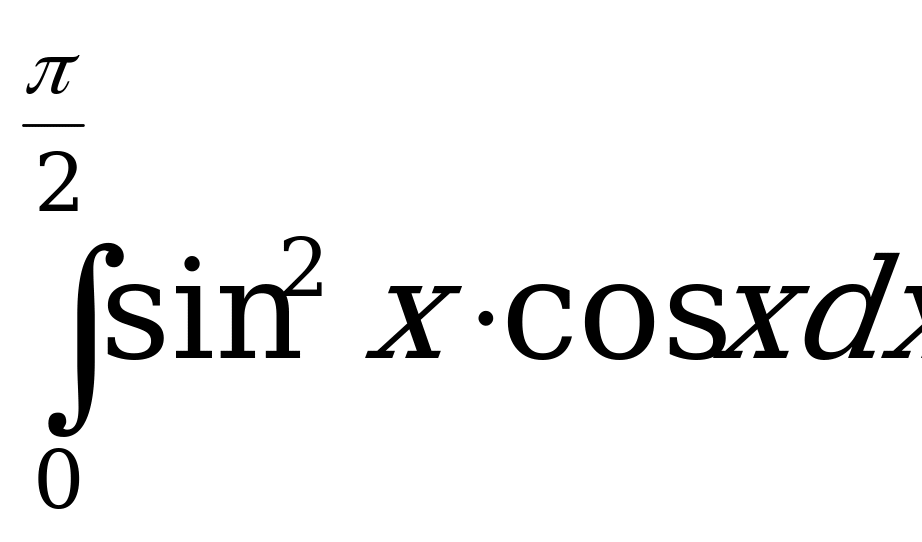 ;
;

















