
Мастер-класс
«Из опыта подготовки к ОГЭ
по математике
Модуль «Геометрия» 1 часть»
Полянская Л. Н., учитель математики
Булгакова Н.Г., учитель математики
МБОУ СОШ № 59

Основной государственный экзамен
Основной государственный экзамен — это основной обязательный вид экзамена в 9 классе средней школы.
ОГЭ - это результат работы ученика и учителя на протяжении всего обучения в школе, и подготовка к нему является важной составляющей учебного процесса.

Наибольший процент нерешенных заданий приходится на модуль «Геометрия»:
- на изучение геометрии в школе отводится в среднем в два раза меньше времени, чем на уроки алгебры;
- навыки построения и чтения чертежей у многих ребят сформированы плохо;
- аналитическое мышление развито не в полной мере
Итог: задания по геометрии зачастую просто игнорируются учащимися.

Цель мастер-класса:
- поделиться с коллегами опытом работы в подготовке учащихся к ОГЭ модуль «Геометрия».
Задачи:
- показать систему подготовки учащихся к ОГЭ
- определить объём необходимых знаний для успешной сдачи экзамена, продемонстрировать типовые задачи (шаблоны)
- решить совместно модуль «Геометрия» из первой части Демоверсии ОГЭ, как официального источника демонстрационного варианта

система подготовки
При подготовке учащихся к ОГЭ учителю необходимо:
- формировать у учащихся навыки самоконтроля;
- выполнять систематически контроль теоретических знаний ;
- формировать умения проверять ответ на правдоподобие;
- систематически отрабатывать вычислительные навыки;
- формировать умение переходить от словесной формулировки соотношений между величинами к математической;
- учить проводить доказательные рассуждения при решении задач;
- учить записывать математические рассуждения, доказательства, обращая внимание на точность и полноту проводимых обоснований.

При подготовке к ОГЭ следует знать специфику класса и уровень знаний по предмету.

типовые задачи
Задание №15
Планиметрическая задача с практическим содержанием.
1й тип задач
1)Какой угол (в градусах) образуют минутная
и часовая стрелки часов в 18:00?
Решение. стрелки образуют развернутый угол, а он равен 180°.
Ответ: 180.
2) Какой угол (в градусах) описывает минутная
стрелка за 4 минуты?
Решение. Сначала найдем, сколько в одной
минуте градусов. Так как в круге 60 минут и 360 градусов, то
360 : 60 = 6 градусов – в одной минуте, а в 4 минутах: 6 • 4 = 24º
Ответ: 24.

3) На какой угол (в градусах) поворачивается минутная стрелка, пока часовая проходит 2°?
Решение. Минутная стрелка движется в 12 раз быстрее часовой, поэтому она пройдет 24°.
Ответ: 24
4) Какой угол (в градусах) образуют минутная и часовая стрелки в 5 ч?
Решение. Часовыми делениями циферблат разбит на 12 равных центральных углов с градусной мерой 360º : 12 = 30 градусов. Между минутной и часовой стрелками пять часовых делений.
Они образуют угол 150°.
Ответ: 150.

5) Колесо имеет 18 спиц. Углы между соседними спицами
равны. Найдите угол, который образуют две соседние
спицы. Ответ дайте в градусах.
Решение. 18 спиц делят окружность колеса на 18 равных центральных углов, сумма которых равна 360°. Поэтому величина одного такого угла будет равна 360º : 18 = 20
Ответ: 20.
6) На рисунке изображено колесо с пятью спицами.
Сколько спиц в колесе, в котором угол между любыми
соседними спицами равен 15°?
Решение. Колесо представляет собой круг. Количество спиц совпадает с количеством секторов, на которые ими оно делится. Так как развёрнутый угол 360°, а угол между спицами равен 15°, имеем: 360º:15=24. Поэтому в колесе 24 спицы.
Ответ: 24.

2й тип задач
7) Площадь прямоугольного земельного участка равна 9 га, ширина участка равна 150 м. Найдите длину этого участка в метрах.
Решение. Переведем площадь участка в квадратные метры:
9 га = 90 000 м 2 .
Площадь прямоугольника равна произведению его смежных сторон. Поэтому, длина участка равна: 90 000 : 150 = 600 м.
Ответ: 600 .
8) Найдите периметр прямоугольного участка земли, площадь которого равна 800 м 2 и одна сторона в 2 раза больше другой.
Ответ дайте в метрах.
Решение. Пусть x м — ширина участка, тогда длина — 2x м. Так как площадь прямоугольника равна произведению его смежных сторон,
То откуда х=20 – ширина. Соответственно 40 м – длина.
Периметр прямоугольника метров.
Ответ: 120.

9) Сколько досок длиной 3,5 м, шириной 20 см и толщиной 20 мм выйдет из четырехугольной балки длиной 105 дм, имеющей в сечении прямоугольник размером 30 см 40 см?
Решение. Найдем объем доски: 350 · 20 · 2 = 14 000 см 3 . Найдем объем балки: 1050 · 30 · 40 = 1 260 000 см 3 .
Поэтому количество досок равно 1 260 000 : 14 000 = 90.
Ответ: 90.

3й тип задач
10) Проектор полностью освещает экран A высотой
80 см, расположенный на расстоянии 250 см от
проектора. На каком наименьшем расстоянии
(в сантиметрах) от проектора нужно расположить
экран B высотой 160 см, чтобы он был полностью
освещён, если настройки проектора остаются неизменными?
Решение. Заметим, что высота экрана, расположенного на расстоянии 250 см, в 2 раза меньше высоты экрана, расположенного на искомом расстоянии, значит, по теореме о средней линии, искомое расстояние в два раза больше первоначального экрана:
250·2 = 500см.
Ответ: 500.
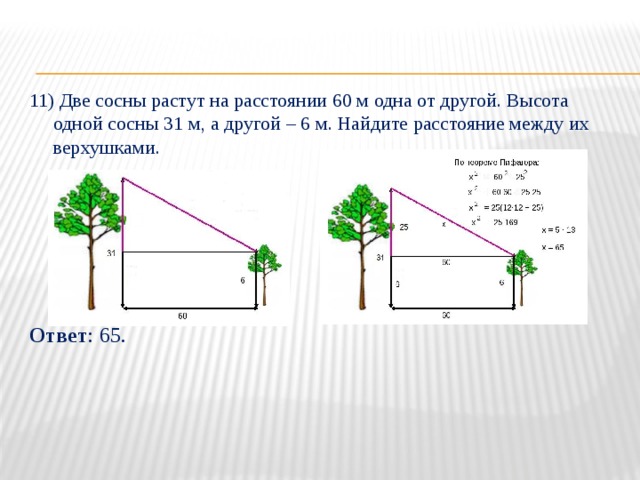
11) Две сосны растут на расстоянии 60 м одна от другой. Высота одной сосны 31 м, а другой – 6 м. Найдите расстояние между их верхушками.
Ответ : 65.

12) Человек ростом 1,7 м стоит на расстоянии 8 шагов от фонаря. Длина тени человека равна четырём шагам шагам. На какой высоте (в метрах) висит фонарь?
Решение.
Сначала найдем расстояние (в шагах)
от фонаря до крайней точки тени:
4+8 = 12 шагов.
Прямоугольные треугольники подобны
с коэффициентом подобия k = 12 : 4 = 3.
Значит, высота фонаря в 3 раза больше роста человека
1,7 ∙3 = 5,1(м)
Ответ: 5,1.

Задание16 Многоугольники и их элементы
1) В треугольнике ABC известно, что угол BAC = 48°, AD — биссектриса. Найдите угол BAD. Ответ дайте в градусах .
Решение. Так как AD биссектриса угла BAC, то она делит этот угол пополам. Следовательно, угол BAD представляет собой половинку угла BAC и равен:
Ответ: 24
2) Сторона треугольника равна 16, а высота,
проведённая к этой стороне, равна 19. Найдите площадь этого треугольника.

Решение.
Площадь треугольника равна половине произведения высоты на основание, к которому эта высота проведена. В задании дано значение высоты h=19 и длина основания a=16. Тогда площадь треугольника равна:
Ответ: 152
3)В треугольнике ABC известно, что АС = 32, ВМ — медиана, ВМ = 23. Найдите AM.
Решение.
Так как BM – медиана, опущенная на сторону AC, то точка M делит сторону AC пополам, то есть и .
Ответ: 16

4) Один из острых углов прямоугольного треугольника равен 57°. Найдите его другой острый угол. Ответ дайте в градусах.
Решение.
Так как сумма острых углов прямоугольного треугольника 90 градусов, то неизвестный угол будет равен 90º-57º=33º .
Ответ: 33

5) Сторона равностороннего треугольника равна 16√3 . Найдите его высоту.
Решение.
В равностороннем треугольнике все стороны равны, а углы составляют по 60 градусов. В таком треугольнике высота, проведенная из любого его угла является также и медианой .
Найдем высоту из прямоугольного треугольника,
у которого известна гипотенуза и угол в 60
градусов, лежащий напротив высоты,
тогда противолежащий катет (высоту) можно вычислить как
Ответ: 24

6) В равнобедренном треугольнике ABC с основанием AC внешний угол при вершине A равен 111 °. Найдите величину угла ABC. Ответ дайте в градусах.
Решение.
Внешний угол – смежный угол с углом А. Сумма смежных углов равна 180°. ∠А=180°–111°=69°. В равнобедренном треугольнике углы при основании равны, поэтому ∠A=∠C=69°. Сумма углов треугольника АВС равна 180°. ∠В=180°–∠А–∠С=180°–69°–69°=42°. О т в е т :42

7) Точки М и N являются серединами сторон АВ и ВС треугольника ABC, сторона АВ равна 57, сторона ВС равна 74, сторона АС равна 48. Найдите MN.
Решение.
По условию задачи отрезок MN является средней линией треугольника ABC и параллельна основанию AC (то есть MN перпендикулярна AC по определению средней линии треугольника). Кроме того известно, что длина средней линии в 2 раза меньше длины основания, которому она параллельна, то есть
Ответ: 24

,
Задание 17 Окружность, круг и их элементы.
1)Точка О — центр окружности, на которой лежат точки А, В и С. Известно, что углы ABC = 69° и OAB = 48°. Найдите угол ВСО. Ответ дайте в градусах.
Решение
Угол ABC является вписанным углом, опирающийся
на дугу AC. Известно, что градусная мера дуги, на которую опирается вписанный угол в 2 раза больше этого угла, то есть
Угол AOC – центральный и равен градусной мере дуги AC, на которую он опирается, то есть
Рассмотрим треугольник AOC – равнобедренный, так как AO=OC – радиусы окружности. Углы при основании этого треугольника равны, а сумма всех углов 180°, следовательно,
=

.
и угол BCO равен
Ответ : 21
2) Площадь круга равна 88. Найдите площадь сектора этого круга, центральный угол которого равен 90°.
Решение.
Если центральный угол равен 90°, то закрашенный
сектор в точности равен 1/4 от всего круга, так как 90:360=1:4. Так как вся площадь круга 88, то площадь сектора будет равна 88:4=22.
Ответ: 22.

3) На окружности по разные стороны от диаметра АВ взяты точки М и N. Известно, что угол NBA = 36°. Найдите угол NMB. Ответ дайте в градусах.
Решение.
NBA является вписанным углом и
опирается на дугу AN, следовательно, градусная мера дуги AN равна:
Градусная мера дуги AB равна 180 , так как это диаметр окружности, который делит круг в 360 пополам. Тогда градусная мера дуги NB равна
На дугу NB опирается вписанный угол NMB, который равен половине градусной меры дуги NB:
Ответ: 54.

4) Длина хорды окружности равна 72, а расстояние от центра окружности до этой хорды равно 27. Найдите диаметр окружности.
Решение
Проведём отрезок АО. Рассмотрим треугольник
АОВ. Данный треугольник прямоугольный, так как
ОВ – высота. АВ равно половине длины хорды. Тогда, по теореме Пифагора:
отсюда :
АО=45 – радиус окружности.
Следовательно, диаметр равен 90.
Ответ: 90.

5) В треугольнике ABC известно, что АС = 8, ВС = 15, угол С равен 90°. Найдите радиус описанной около этого треугольника окружности.
Решение.
Радиус описанной около прямоугольного треугольника
окружности равен половине его гипотенузы.
Найдем гипотенузу AB треугольника ABC
по теореме Пифагора:
и радиус равен
Ответ: 8,5

Задание 18 площади, периметры фигур и их элементы.
1)Диагонали АС и BD трапеции ABCD с основаниями ВС и AD пересекаются в точке О, ВС = 7, AD = 9, АС = 32. Найдите АО.
Решение.
Треугольники BCO и AOD
подобны друг другу. Следовательно, можно записать
отношение
то есть точка O делит отрезок AC в отношении 7:9, отсчитывая от вершины C. Это означает, что весь отрезок AC можно разделить на 7+9=16 равных частей, 7 из которых составляет OC, а 9 – AO, то есть:
Ответ: 18.

2)В ромбе АВСD угол ABC равен 134 . Найдите угол ACD.Ответ дайте в градусах.
Решение
Сумма всех углов в ромбе равна 360 , а
противоположные углы равны. Следовательно,
угол BCD равен:
Диагональ АС ромба является также биссектрисой углов BAD и BCD, следовательно, угол ACD в 2 раза меньше угла BCD:
Ответ:23.

.
3) Сторона ромба равна 8, а расстояние от точки пересечения диагоналей ромба до неё равно 2. Найдите площадь этого ромба.
Решение
Площадь ромба можно найти по формуле
площади параллелограмма, так как ромб – это частный случай параллелограмма. Площадь будем искать как произведение высоты h ромба на длину стороны a , к которой эта высота проведена. Высота ромба равна
Таким образом, площадь ромба равна
Ответ: 32

4) В равнобедренной трапеции основания равны 3 и 9, а один из углов между боковой стороной и основанием равен 45°. Найдите площадь трапеции.
Решение
Введём обозначения, как показано на
рисунке. Тогда
Треугольник AKB прямоугольный и равнобедренный, тогда высота ВК равна 3.
Откуда
Ответ: 18.

Задание 19 фигуры на клетке
1)На клетчатой бумаге с размером клетки 1x1 изображён треугольник. Найдите его площадь.
2) На клетчатой бумаге с квадратними
клетками изображён треугольник АВС.
Найдите тангенс угла С.
3) На клетчатой бумаге с клетками размером 1 см×1см изображён треугольник . Найдите его площадь в квадратных сантиметрах.

4)На клетчатой бумаге с размером клетки 1×1 изображён треугольник АВС. Найдите длину его средней линии, параллельной стороне АС.
5) На клетчатой бумаге с размером
клетки 1×1 изображён прямоугольный
треугольник . Найдите длину его
большего катета.
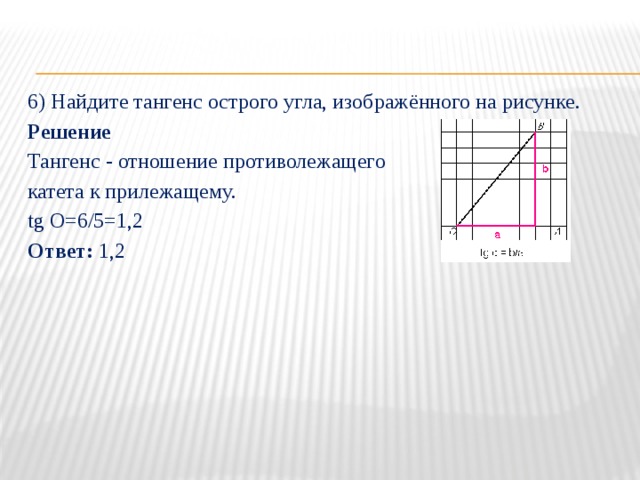
6) Найдите тангенс острого угла, изображённого на рисунке.
Решение
Тангенс - отношение противолежащего
катета к прилежащему.
tg О=6/5=1,2
Ответ: 1,2

Задание 20 Анализ геометрических утверждений
№ 1Какое из следующих утверждений верно?
1) Если две стороны одного треугольника соответственно равны двум сторонам другого треугольника, то такие треугольники равны.
2) Точка пересечения двух окружностей равноудалена от центров этих окружностей.
3) Диагонали ромба точкой пересечения делятся пополам.
В ответе запишите номер выбранного утверждения.
Решение.
1) Неверно. Нужно чтобы еще угол между ними был равен.
2) Неверно. Если окружности имеют разные радиусы, то точка пересечения не будет равноудалена от их центров.
3) Верно.
Ответ: 3.

№ 2 Какое из следующих утверждений верно?
1) Касательная к окружности параллельна радиусу, проведённому в точку касания.
2) Диагонали ромба точкой пересечения делятся пополам.
3) Внешний угол треугольника равен сумме его внутренних углов.
Решение.
1) Неверно, касательная к окружности перпендикулярна радиусу, проведённому в точку касания.
2) Верно.
3) Неверно. Внешний угол треугольника равен 180 градусов минус угол треугольника, к которому он примыкает или внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним.
Ответ: 2 .

№ 3.Какое из следующих утверждений верно?
1) Боковые стороны любой трапеции равны.
2) Через любую точку, лежащую вне окружности, можно провести две касательные к этой окружности.
3) Площадь квадрата равна произведению его диагоналей.
В ответ запишите номер выбранного утверждения.
Решение.
1) Неверно, боковые стороны у трапеции могут различаться по длине.
2) Верно. Из внешней точки окружности можно провести только две касательные к этой окружности.
3) Неверно. Площадь квадрата равна половине произведения его диагоналей.
Ответ: 2

4) №4 Какое из следующих утверждений верно?
1) Через точку, не лежащую на данной прямой, можно провести прямую, параллельную этой прямой.
2) Треугольник со сторонами 1, 2, 4 существует.
3) Если в ромбе один из углов равен 90градусов, то такой ромб — квадрат.
Решение.
1)Верно. Так как по аксиоме параллельных прямых. Через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной. Значит можно провести такую прямую.
2) Неверно. Сумма любых двух сторон БОЛЬШЕ третьей стороны,а здесь 1+2
3) Верно. Противоположные углы в ромбе равны, значит 90 и 90сумма односторонних = 180 градусов. Вывод все углы = 90 в ромбе все стороны равны, значит это КВАДРАТ.
Ответ: 13

№ 5. Какие из следующих утверждений верны?
1) Любые два равносторонних треугольника подобны.
2) В любом прямоугольнике диагонали взаимно перпендикулярны.
3) Все диаметры окружности равны между собой.
В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Решение.
1) Верно. Равносторонние треугольники подобны, так как углы в нем все равны по 60 градусов, следовательно, они подобны по 2 углам.
2) Неверно. В прямоугольнике диагонали могут пересекаться под разными углами, в том числе и под прямым.
3) Верно. Диаметр окружности —отрезок, соединяющий две точки на окружности и проходящий через центр окружности. Соответственно, при любом повороте диаметра, расстояние между такими точками всегда одно и то же.
Ответ: 13.

№ 6. Какие из следующих утверждений верны?
1) Длина гипотенузы прямоугольного треугольника меньше суммы длин его катетов.
2) Если точка лежит на биссектрисе угла, то она равноудалена от сторон этого угла.
3) Если диагонали параллелограмма равны, то он является ромбом.
В ответе запишите номера выбранных утверждений без пробелов,
запятых и других дополнительных символов.
Решение.
1) Верно . Длина гипотенузы всегда меньше сумм катетов прямоугольного треугольника.
2) Верно. Так как биссектриса делит угол пополам, то расстояние от нее до противоположных сторон угла будет одинаковым.
3) Неверно. Диагонали у ромба должны пересекаться под прямым углом и не обязательно быть равными.
Ответ: 12.

№ 7 Какое из следующих утверждений верно?
1) В параллелограмме есть два равных угла.
2) В тупоугольном треугольнике все углы тупые.
3) Площадь прямоугольника равна произведению длин всех его сторон.
Решение .
1.Верно. В параллелограмме противоположные углы равны. Значит имеется 2 пары равных углов.
2.Неверно. Если бы в треугольнике было хотя бы два тупых угла (то есть больше 90 градусов) то сумма этих двух углов уже была бы больше 180 градусов. Если в треугольнике один угол тупой, то два остальных только острые. В сумме эти три угла должны дать 180 градусов.
3.Неверно. Площадь прямоугольника равна произведению длин двух его смежных сторон.
Ответ: 1

Спасибо за внимание!
































































