Организация учебного процесса
Ещё десять- пятнадцать лет назад вопрос «математической культуры» прозвучал бы дико для российских школьников, преподавателей. Однако в последние годы выясняется, что для большинства юношей и девушек сущность «математических» рассуждений остаётся тайной за семью печатями. Им приходится с трудом постигать азбуку логических построений. Научиться чётко представлять, что надо доказывать утверждение как теорему или привести контрпримеры; что в математике существуют необходимые и достаточные условия, причины и следствия; что система уравнений и их совокупность разные вещи; что понятие равносильности неравенств или уравнений не заучивается, а формулируется самостоятельно. Все эти смысловые тонкости и составляют понятие «математической культуры»
Вооружить учащихся опорным уровнем знаний, выработать у них
прочные математические знания – одно из важнейших программных
требований, выполнение которого при обучении математики требует от учителя и учеников немало усилий. И хотя в основе современного школьного курса лежат математические правила, выкладки, доказательства, это ещё не обеспечивает учащихся знаниями.
Успех обучения математике определяется не столько знанием правил, а их пониманием, умением применять их. Ведь выявить внутреннее содержание правила удаётся далеко не всем, и тогда теория усваивается формально и не даёт ощутимых результатов в обучении. Значительная часть учащихся, не применяет правила при решении заданий, потому что не видит, в каких случаях можно допустить ошибку.
Учитывая данный факт, при планировании работы по выработке вычислительных навыков (что является неотъемлемой частью каждого урока математики) использую принцип этапности.
Начальным этапом (первым) считаю не только психологическую подготовку, но и, обязательно устную работу. Данный вид работы позволяет не только непрерывно тренировать математические навыки, но и делают материал более доступным, что не только отражается на качестве знаний, но и сокращает время работы над заданиями. Задания, используемые на данном этапе, не отличаются разнообразием, но при регулярном их использовании дают продуктивный результат. Предлагаю некоторые из них:
• «Действия с десятичными дробями»
Данные задания помогают ученику узнать секреты устного счёта
7
Михайлюк Светлана Ивановна
3,9:0,3 0,55:0,11 6·0,5 4·1,5 4·2,5
2,5:0,5 0,63:0,09 12·0,5 8·1,5 6·2,5
4,2:0,7 1,44:0,12 36·0,5 16·1,5 12·2,5
Такие упражнения позволяют ученикам сделать вывод: если у делимого и у делителя одинаковое число знаков после запятой, то при делении десятичных дробей, на запятую внимание не обращают; умножить на 0,5 значит разделить на 2; умножить на 1,5 значит к целому прибавить половину; умножить на 2,5 значит к двум целым прибавить половину.
• «Действия с обыкновенными дробями»
8·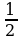 ; 16·
; 16·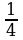 ; 25·
; 25·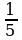 ; 28·
; 28·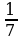 ; 36·
; 36·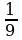 .
.
Эти упражнения говорят о том, что умножить целое число на 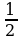 ;
; 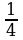 ;
;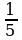 ;
;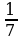 ;
;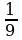
Значит, разделить на 2, 4, 5,7, 9.
• «Дробные выражения»
Для учащихся 7-9 классов можно включить задания с алгебраическими выражениями
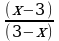 ;
; 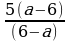 ;
; 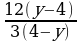 ;
; 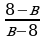 ;
;
Этот вид заданий обучает учащихся видеть правило сокращения дроби (при делении выражений с противоположными знаками получится -1).
Считаю нужным добавить, что данные виды заданий устного плана целесообразно использовать ежеурочно как элементы разминки для регулярного тренинга.
Вторым этапом данного вида работы является процесс повторения ранее изученного. Он может быть осуществлён разными способами.
• «Использование большой динамической пары»
Данный приём моей работы заключает следующее: каждый ученик класса должен опросить другого (всех учеников класса) и ответить на их вопросы. Чтобы воспитать у учащихся ответственность за порученную работу и поощрить тех, кто хочет поскорее ответить сам, не опрашивая остальных,
8
Михайлюк Светлана Ивановна
подчёркиваю, что оценка за повторение будет поставлена тому, кто опросил
всех. Причём разрешаю вести опрос не только на уроке, но и на перемене. Если ученик опросил всех, ему выставляю оценку за повторение почти всегда высокую, а затем он получает следующее небольшое задание для опроса.
Во время работы в динамической паре дети свободно пересаживаются, говорят в пол голоса, что раскрепощает детей, стоит рабочий шум. И всё же это вызывает нарушение дисциплины, поэтому работу в большой динамической паре провожу изредка, когда необходимо освежить в памяти большой раздел.
• «Игра Карусель»
Участвуют все ученики, желательно, чтобы их было чётное число.
Ученики становятся в два круга (внешний и внутренний), становятся лицом к лицу, образуя пару. По сигналу учителя внешний круг начинает двигаться, а внутренний стоит на месте (т.е. сдвинувшись на шаг вправо, ученик меняет пару), за время, которое даёт учитель, ученики должны задать вопрос партнёру, выслушать его ответ и ответить самому на вопрос, который ему задаёт партнёр. Затем учитель подаёт сигнал, и ученик делает опять шаг
вправо. И так продолжается до тех пор, пока каждый не вернётся к исходной
паре. Ученик может задавать всем один и тот же вопрос, но в итоге сам он ответит на несколько.
• «Диаграмма Вена»
Это оригинальный способ для повторения и обобщения ранее изученного. Для диаграммы можно использовать различные геометрические фигуры. Обычно я строю две пересекающиеся окружности, их размер зависит от того, сколько мы будем писать. В каждой образовавшейся при пересечении части, ученик должен записать свойства, касающиеся только данной фигуры, а на пересечении –общее для двух фигур. Это позволяет повторить конкретное, выявить общее и отличительное. Например, параллелограмм и прямоугольник. В общей части (там, где пересеклись окружности) ученики записывают общее для параллелограмма и прямоугольника (четырёхугольники, противоположные стороны параллельны и равны…), а в остальных частях только то, что характерно для данных фигур. Можно сравнивать сразу несколько фигур (Приложение 1).
• «Разорванные цепи»
Этот приём я применяю для повторения определений, теорем. Суть
заключается в следующем, необходимо заранее напечатать это определение и
9
Михайлюк Светлана Ивановна
дать ученику, но не сплошным текстом, а по слову в разброс. Ученик должен собрать из предложенных слов определение или теорему (Приложение 1,3).
• «Кластер»
Данное задание, как мозговой штурм, помогает создать общую картину по теме. То есть берётся ключевое слово (например «трапеция»), ученикам предлагают называть все ассоциации, идеи связанные с этим словом. Ученики могут называть всё, что им придёт в голову. В результате собирается материтал, выводим основное и формулируем определённое правило, взгляды, расшифровываем формулы. С кластером можно работать несколько уроков. Можно дополнять новыми идеями, можно использовать как вопросник (Приложение 2).
Третьим этапом
в выработке вычислительных навыков (считаю нужным заметить в очередной раз, что данное деление условно, так как вычислительная работа, а также решение задач- неотъемлемый компонент каждого урока математики) является контроль полученных знаний.
Отмечу, что использую в работе различные виды контроля: самоконтроль, взаимоконтроль, контроль со стороны учителя.
На этом этапе использую различные задания, зависящие от того, какой вид деятельности проверяется:
1. Тестирование.
2. Самостоятельные работы.
3. Математические диктанты.
4. Контрольные работы.
5. Мини – проверочные работы.
Чаще всего, в собственной практике применяю такой вид тестирования, как тест- обучающие программы (Приложение 4).
Это обусловлено тем, что я столкнулась с проблемой: приучения учащихся самостоятельно решать задачи и организации посильной работы для каждого ученика. Стремясь решить эту проблему, я стала применять тест- обучающие программы по Хамитову по различным темам алгебры и геометрии. Каждая программа включает 100
заданий трёх уровней. Первый уровень требует знания определений, формул, теорем и т.д.; второй уровень- умения применять их на практике; третий уровень задания, выходящие за пределы обязательного обучения.
Для тестирования предлагаются 10 вариантов. Варианты 1-5 соответствуют первому уровню, в который входят, как правило, вопросы
10
Михайлюк Светлана Ивановна
обязательного уровня обучения; варианты 6-10- второму уровню, который требует более глубокого знания изучаемого материала. Программа разработана таким образом, что ученик получает оценку автоматически (смотрите приложение 4).
Регулярно применяя изложенный в разделе «Организация учебного процесса», материал, отметила, рост познавательной активности, качества знаний. Исходя из этого я пришла к выводу, что навыки вычислительной работы, относящиеся к числу сложнейших , требуют непрерывной целенаправленной работы, и лишь дифференцированный подход к каждому ученику, осуществляемый на уроках с тщательным подбором материала, с использованием средств наглядности, предусматривает высокие результаты.







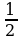 ; 16·
; 16·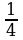 ; 25·
; 25·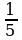 ; 28·
; 28·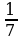 ; 36·
; 36·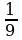 .
.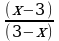 ;
; 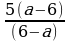 ;
; 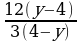 ;
; 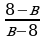 ;
; 




















