Ортогональное проецирование

Ортогональное проецирование

Oртогональное проецирование — это частный случай параллельного проецирования. При ортогональном проецировании проецирующие лучи перпендикулярны к плоскости проекций.

Аппарат такого проецирования состоит из одной плоскости проекций.

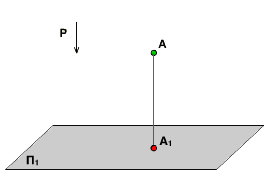
Чтобы получить ортогональную проекцию точки А, через неё надо провести проецирующий луч перпендикулярно к П1. Точка А1 называется ортогональной или прямоугольной проекцией точки А.

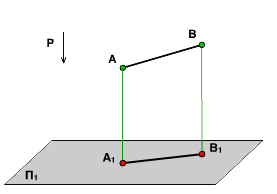
Чтобы получить ортогональную проекцию А₁В₁ отрезка АВ, на плоскость П₁, необходимо через точки А и В провести проецирующие прямые, перпендикулярные П₁. При пересечении проецирующих прямых с плоскостью П₁ получатся ортогональные проекции А₁ и В₁ точек А и В. Соединив ортогональные проекции А₁ и В₁ получим ортогональную проекцию А₁В₁ отрезка АВ.

Все свойства параллельного проецирования выполнимы и для ортогонального проецирования. Однако ортогональные проекции обладают ещё некоторыми свойствами.

Свойства ортогонального проецирования:
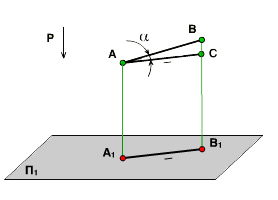
1. Длина отрезка равна длине его проекции, делённой на косинус угла наклона отрезка к плоскости проекций.

Возьмём прямую АВ и построим её ортогональную проекцию А₁В₁ на плоскость П₁. Если провести прямую АС || А₁В₁, то из треугольника АВС следует, что |АС| : |АВ| = cos  или |АВ| = |А₁В₁| : cos , т. к. |А₁В₁| = |АС|.

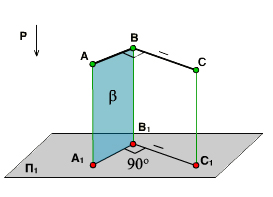
2. Кроме того, для ортогонального проецирования будет справедлива теорема о проецировании прямого угла:

Теорема:  Если хотя бы одна сторона прямого угла параллельна плоскости проекций, а вторая ей не перпендикулярна, то угол на эту плоскость проецируется в натуральную величину.

Доказательство:

Дан прямой угол АВС, у которого по условию прямая ВС  АВ и ВС || плоскости проекций П₁. По построению прямая ВС 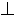 к проецирующему лучу ВВ₁. Следовательно, прямая ВС  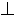к плоскости  (АВхВВ1), т. к. она  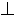к двум пересекающимся прямым , лежащим в этой плоскости. По условию прямая В₁С₁ || ВС, поэтому тоже  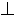к плоскости , т. е. и прямой А₁В₁ этой плоскости. Следовательно, угол между прямыми А₁В₁ и В₁С₁ равен 90°, что и требовалось доказать.

Ортогональное проецирование обеспечивает простоту геометрических построений при определении ортогональных проекций точек, а так же возможность сохранять на проекциях форму и размеры проецируемой фигуры. Эти достоинства обеспечили ортогональному проецированию широкое применение в техническом черчении.