Орус окумуштуусу математик Николай Иванович Лобачевский

                               Николай Иванович Лобачевский

                                (1792-1856)

                                  Орустун улуу математиги

Дүйнөнүн көп математиктери кылымдар бою Евклиддин бешинчи постулатын далилдөө менен алышып келишкен, бирок орус окумуштуусу гана бешинчи постулаттын башкалардан көз карандысыздыгы жөнүндөгү гениалдуу ачылыш жасаган. Ошонун негизинде Лобачевский Евклиддин геометриясынан айырмалуу башка геометрияны түзү мумкүн экендигин далилдеген: мындай геометрия Лобачевскийдин геометриясы деп аталат.  Николай Иванович Лобачевский 1792-жылы 1 декабрде төрөлгөн. Анын атасы майда чиновник болгон. Атасы өлгөндөн кийин ал жаш кезинде эле жетим калган. Ошол моменттен баштап анын өмүрү Казань шаары менен байланыштуу болгон.Казандагы гимназияны бүтүргөн соң ал Казань универистетин бүтүрүп анын профессору жана ректору болуп эмгектенген. Өзү тирүү кезинде Лобачевскийдин сиңирген эмгеги татыктуу бааланган эмес. Ал убакытты артка таштап озунуп эмгектенген. Лобачевскийдин идеясын дүйнө тааныгандан кийин гана геометрияда жаңы эра башталган. Лобачевский башка да толуп жаткан эң мыкты ачылыштарды жасаган, бирок ошентсе да алардын эң негизгиси Лобачевскийдин геометриясынын ачылышы болуп эсептелет.

        Жогоруда айтылгандай Евклиддин V постулатын далилдөөгө карата көп кылымдар бою жасалган аракеттер ХIХ кылымдын башында жаңы геометриянын ачылышына алып келди. Бул жаңы геометриянын ачылышы биринчи жолу Николай Иванович Лобачевскийдин «Геометриянын башталышы жөнундө» деген эмгегинде 1829-жылы жарыяланган. Бирок, бул жаңылыкты ачкандыгы жөнүндө докладды ал 1826-жылы 11-февралда Казан универистетинин физика-математика факультетинин заседаниесинде жасаган.

       Ошондуктан 1826-жылдын 21-февралын (эски стил боюнча 11-февраль) жаңы, евклиддик эмес геометриянын ачылыш датасы деп эсептешет.Н.И.Лобачевскийдин ошондо жасаган доклады «Параллель түз сызыктар жөнүндөгү көрсөтүлгөн геометриянын башталышынын кыскача баяндалышы» деп аталып,француз тилинде жазылган. Ушул докладында жаңы геометриянын негизи баяндалган.

            Н.И.Лобачевский Казан универистетинде окутуучу болуп иштей баштаган учурунун алгачкы жылдарында эле Евклиддин V постулатын далилдөөгө аябай аракет кылган.Өзунун V постулатты далилдөөгө жасаган аракетинин ийгиликсиз аякташы жана андан мурдагы окумуштуулардын да аны далилдөөлөрүнун ийгиликсиз болушу Н.И. Лобачевскийди жаны идеяга,пикирге алып келген: Евклиддин V постулатын (параллелдик аксиомасын) далилдөөгө болбойт,анткени анын тууралыгы Евклиддин геометриясынын калган аксиомаларынан келип чыкпайт, эгерде V постулатты, б.а. анын параллелдик аксиомасын жокко чыгарып тануучу (же ага карама-каршы болгон) аксиоманы кабыл алсак, анда ал бизди жаңы геометрияга алып келет. Чындыгында эле, Н.И. Лобачевский Евклиддин параллелдик аксиомасын жокко чыгарып, б.а. «тегиздикте берилген туз сызыктан тышкары жаткан чекит аркылуу ага параллель болгон жок дегенде эки түз сызык жүргүзүүгө болот» деп эсептеп, ошондой эле Евклиддин калган аксиомаларын ошол бойдон кабыл алып, эч кандай карама-каршылыкка учурабаган көп теоремаларды далилдеген.Ал теоремалар логикалык жактан туура болгон, бирок, алар Евклиддин геометриясындагы теоремалардан таптакыр айырмаланган.Алар жаңы геометриянын теоремалары болуп эсептелген. Лобачевский өзүнүн бул жаңы геометрясын «Элестетүүчү геометрия» деп атаган. Н.И.Лобачевскийдин геометрия боюнча чоң ачылыш жасагандыгы жогору  баланып, аны «геометриянын Коперниги» деп аташкан.

            Кылымдар бою өкум сүрүп келген Евклиддик геометриянын окумуштуулардын аңсезимине сиңип калышы,жаны геометрияны кабыл алууга кыйла тоскоолдук кылган. Ал-бетте, ал кезде мындай жаңы геометрия алар үчүн таң калаарлык болуп көрүнөт эле. Ошентип, Лобачевскийдин геометриясы ал убакта (өзүнүн тирүүсүндө) толук кабыл алынган эмес. Лобачевский Евклиддин V постулатына, б.а. параллелдик аксиомасына карама-каршы болгон төмөндөгүдөй аксиоманы кабыл алган.

             . а каалагандай түз сызык, А ал түз сызыкта жатпаган чекит болсун. Бул түз сызык жана чекит аркылуу аныкталган тегиздикте А чекити аркылуу өтүп, а түз сызыгы менен кесилишпей турган жок дегенде эки түз сызык өтөт. Бул Лобачевскийдин аксиомасы деп аталат.

            Лобачевский өзүнүн геометриясын түзгөндө Евклиддин параллелдик аксиомасынан башка анын бардык аксиомаларын, б.а. абсолюттук геометриянын бардык аксиомаларын кабыл алган. Демек, ал Евклиддин параллелдик аксиомасын гана өзгөрткөн. Анда а түз сызыгы жана андан тышкары жаткан А чекити аркылуу өтүп, а түз сызыгы менен кесилишпей турган түз сызыктын бар экендиги абсолюттук геометриянын теоремалары аркылуу негизделет.

Лобачевскийдин аксиомасы боюнча А чекити аркылуу  а  түз сызыгы менен кесилишпей турган жок дегенде эки түз сызык жүргүзүүгө болот. Алар b жана с түз сызыктары болсун. (1- сүрөт). Анда А чекити аркылуу өтүп,   бурчунун ичинде жаткан бардык башка түз  сызыктар да а түз сызыгы менен кесилишпейт.

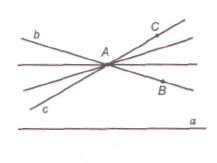
Демек, А чекити аркылуу а түз сызыгы менен кесилишпей турган  чексиз көп түз    сызыктар болот. Лобачевскийдин аксиомасы аткарылат деп эсептелген тегиздикти (мейкиндикти) Лобачевскийдин тегиздиги (мейкиндиги) деп аташат. Ошентип, Лобачевскийдин геометриясынын аксиомалары Евклиддин аксиомаларынан (параллелдик аксиомасынан башка), б.а. абсолюттук геометриянын аксиомаларынан (I-IV группалардагы аксиомалардан) жана Лобачевскийдин аксиомасынан турат. Анда абсолюттук геометриянын аксиомалары, Лобачевскийдин аксиомасы жана андан чыгуучу натыйжалардын чогуусу Лабочевскийдин геометриясын аныктайт.

            Лабочевскийдин геометриясында параллель түз сызыктар кандай аныкталат? деген суроо туулат. а  түз сызыгы жана андан тышкары жаткан А чекити берилсин. Бул берилген чекит менен түз сызык бир тегиздикти аныктайт (2-сүрөт). А чекитинен а түз сызыгына АD га перпендикулярын түшүрөбүз. АD га перпендикулярдуу болгон АЕ шооласын жүргүзөбүз. Анда  АЕ менен  а  түз сызыгы кесилишпейт.   А чекити аркылуу  а  түз сызыгы менен   кесилише турган жана кесилишпей турган чексиз көп түз сызыктарды (шоолаларды) жүргүзүүгө боло тургандыгы белгилүү.

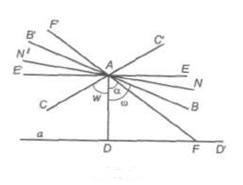
Анда А чекити аркылуу өтүүчү түз сызыктардын (шоолалардын) чогуусун эки топко бөлүүгө болот: кесилишүүчү    жана кесилишпөөчү. Бул учурда АF шооласы биринчи топко, АЕ шооласы экинчи топко тиешелүү болот.   деп эсептейли.     болот.

Эгерде F чекитин а түз сызыгы боюнча оң жакка жылдырсак, анда   бурчу чоңоет, бирок    тан кичине бойдон кала берет. Эгерде F чекити а түз сызыгы боюнча чексиз алыстаса, AF шооласы кандайдыр АВ пределдик абалына ээ болот. Ал шоола кесилишүүчү жана  кесилишпөөчү шоолаларды бөлүп туруучу чектеги шоола болот. Бул акыркы кесилишүүчү шоола же биринчи кесилишпөөчү шоола болот. Бирок, АВ кесилишүүчү шоола боло албайт. Тескерисинче, АВ менен  а  түз сызыгы  М чекитинде кесилишет десек, анда  а  түз сызыгында М чекитинин оң жагынан дагы бир   чекитин табат элек. Бул учурда    шооласы да кесилишүүчү шоола болуп, АВ шооласынын оң жагында жатат эле. Анда АВ бөлүүчү шоола боло албайт эле. Демек, АВ шооласы а түз сызыгы менен кесилишпей турган биринчи шоола.

            Ошондой эле, АВ шооласы АЕ шооласы менен да дал келбейт. Эгерде ал дал келсе, анда Евклиддин параллельдик  аксиомасына ээ болот элек. Бул учурда Лобачевскийдин аксиомасы аткарылбай калат.

            Ошентип, DAB бурчунун ичинде жатуучу ар кандай AF шооласы а түз сызыгын кесип өтөт,ал эми ВАЕ бурчунун ичинде жатуучу ар кандай AN шооласы а түз сызыгын кеспейт .

            Эгерде АD перпендикулярына карата АВ шооласына симметриялуу болгон АС шооласын жүргүзсөк, ал дагы чектеги бөлуп туруучу шоола болот. АВ шооласы кандай касиеттерге ээ болсо, АС шооласы  да ошондой касиеттерге ээ болот.

            AF,АВ,АЕ,АN,АС шоолалары тиешелүү түрдө   түз сызыктарын аныктайт.   бурчунун ичинде жаткан бардык түз сызыктар аны кесет.

            Чектеги   сызыктары гана  а  түз сызыгына параллель деп аталат.

              бурчу параллелдик бурч деп аталат.Ал дайыма   кичине  болот.

            Демек, А чекити аркылуу өтүп, а түз сызыгы менен кесилишпеген түз сызыктардын  бардыгына эле а га параллель деп эсептөөгө болбойт.Мисалы,    түз сызык-тары а га параллель болбойт.

            Ошентип, а түз сызыгына карата А чекити аркылуу өтүүчү түз сызыктардын тобун Лобачевскийдин тегиздигинде үчкө бөлүүгө болот: 

            1.Кесилишүүчү түз сызыктар – алар   ж.б. түз сызыктар.

            2. Параллель түз сызыктар – алар  .

            3.Ажыроочу түз сызыктар – алар    ж.б.

            Лобачевскийдин тегиздигинде параллель түз сызыктардын багыты эске алынат. Мисалы,    түз сызыгы а түз сызыгына D жана   чекитин карай параллель, ал эми    түз сызыгы а түз сызыгына  ны карай параллель деп эсептелет. Эгерде    түз а га параллель болсо, анда а түз сызыгы  түз сызыгына параллель болот (ошол багыт боюнча). Параллельдик белгисин   деп белгилейбиз.

            Эгерде   болсо, анда   болот (белгилүү бир багыт боюнча).

            Жогоруда баяндалгандардын бардыгынын карама-каршы эместигин көрөтүү максатында  алрды кандайдыр бир моделде кароо (текшерип көрүү) оңтойлуу болуп эсептелет . Ал модель А.Кэли (1821-1895, англиялык математик) жана Ф.Клейн (1849-1925, немец математиги) тарабыныан түзүлгөн. Ал Кэли – Клейнидин  модели деп аталат. Албетте, модель каалагандай эле түзүлө бербейт. Лобачевскийдин геометриясындагы негизги обьектилер жана алардын арасындагы байланыштар системасы аткарылгандай моделди түзүү керек.Лобачевскийдин планиметриясын сүрөттөп көрсөтүү (интерпретациялоо) үчүн Евклиддик тегиздикте К ачык тегереги алынган (3-сүрөт). Кэли-Клейндин бул моделинде төмөндөгүдөй «сөздүк» кабыл алынган:

1.      Чекит катарында К тегерегинин ички чекиттерин гана кабыл алабыз. К тегерегинин  айланасында жаткан чекиттер (С,D,М,N) «өздүк эмес» же чексиз алыстатылган чекиттер болуп эсептелет.Ал эми тегеректен тышкары жаткан чекиттер (В,F) «идеалдык» чекиттер деп аталат.

            2. Түз сызык катарында К тегерегинин каалагандай хордасы кабыл алынат. (а,b,с,d ж.б.).

            3. Тегизидик катарында К тегерегинин өзү алынат.

            4. «Тиешелүү», «арасында жатат» деген түшүнүктөр Евклиде кандай алынса мында да ошондой алынат.

            Бул моделде абсолюттук геометриянын I-IV группаларындагы тегиздиктик аксиомалар толук аткарылат. Мисалы, Р жана Q

чекиттери аркылуу тегерекке хорда жүргүзүүгө болот, б.а. түз сызык алыкталат. Мында РQ кесиндисин Лобачевскийдин геометрия метриясындагы кесинди деп эсептөөгө болот, анткени Р менен Q чекиттери сөздүктө кабыл алынган чекиттер. Ал эми QN кесиндисин Лобачевскийдин  геометриясындагы кесинди деп   эсептөөгө болбойт,анткени   N өздүк эмес чекит.  Кэли-Клейндин моделинде  үч бурчтуктарды, кесилишүүчү жана кесилишпөөчү түз сызыктарды  көрсөтүүгө   болот. Мисалы,  А,Р,Q чекиттерин удаалаш туташтырсак АРQ үч бурчтугун алабыз, а жана  d түз сызыктары Е чекитинде  кесилишет, а менен b сызыгы,  а менен с түз сызыгы кесилишпейт. Бул моделде кесиндилердин узундугу жана бурчтун чоңдугу  кыйла татаал формула менен туюнтулат.

Конгурнттуүлүк жөнүндөгү түшүнүк  да ушуга негизделген. Ошондуктан биз буга токтолгонубуз жок. Ошондой болсо да, Лобачевскийдин геометриясынын тегиздиктик аксиомаларын бул моделде текшерүүгө болот.

            Лобачевскийдин аксиомасын текшеребиз, а  туз сызыгын,андан тышкары жаткан  А чекитин алабыз. А чекити аркылуу чексиз көп түз сызык жүргүзүүгө болот, алардын айрымдары а түз сызыгы мен кесилишет, айрымдары кесилишпейт, b жана  түз сызыктары а түз сызыгына параллель деп алынат. Ал а  эми менен с түз сызыктары ажыроочу түз сызыктар болот. Демек, Лобачевскийдин аксиомасы да бул моделде аткарылат.

            Лобачевскийдин геометриясынын планиметрия бөлүгүнүн айрым фактыларын белгилөөгө болот. Албетте, аларды далилдөөгө мүмкүн, биз мында алардын далилденишине токтолгонубуз жок.

1.      Ар кандай үч бурчтуктун ички бурчтарынын смуммасы  тан кичине.

2.      Үч бурчтуктун ички бурчтарынын суммасы   тан кичине болу менен бирге турактуу эмес,  ал бир үч бурчтуктан экинчи үч бурчтукка өткөндө өзгөрүп турат.

3.      Эки үч бурчтуктун туура келүүчү үч бурчтары барабар (конгруэнттүү) болсо, анда    ал үч бурчтуктар конгруэнттүү болушат.

4.      Ар кандай эки түз сызык жалпы эки перпендикулярга ээ болбойт.

Демек, Лобачевскийдин тегиздигинде тик бурчтук деген жок.

 Мунун натыйжасында параллель түз сызыктардын арасындагы аралык турактуу

эмес  экендигин байкайбыз. Алар параллелдик багыты боюнча бири-бирине чексиз жакындайт,ал эми карама – каршы багытта бири-биринен алыстайт.

            Ажыроочу эки түз сызык бир гана жалпы перпендикулярга ээ болот. Ал перпендикуляр алардын арасындагы эң кыска аралыкты аныктайт. Ажыроочу түз сызыктар ал жалпы перпендикулярдан алыстаган сайын бир-биринен ажырай баштайт. Демек, бир түз сызыкка түшүрүлгөн эки перпендикуляр ажыроочу түз сызыктар болушат.

            Н.И. Лобачевскийдин  гениалдуу эмгегинин мааниси өтө зор жана көп грандуу. Аннын  эмгегинин маанисин төмөндөгүдөй айрым фактылар менен белгилеп көрсөтуугө болот:

            а) Н.И. Лобачевский тарабынын түзүлгөн жаңы геометрия илимге, анын ичинде

геометрия илимине зор ревалюция жасады. Эки миң жылдар бою окумуштуулар геометриянын  аксиомаларын өзгөртүүгө мүмкүн эмес деп эсептеп келишкендиги белгилүү, Н.И. Лобачевский болсо, илимдин өсүп өнүгүү процесинде аксиомаларды текшерүүгө, тажрыйбанын   негизинде тактоого жана өзгөртүүгө Евклиддин V постулатын, б.а. параллелдик аксиоманы ага карама – каршы аксиома менен алмаштырып жаңы, Евклиддик эмес геометрияны түздү. Гоеметрия жаңы өсүшкө ээ болду.

б) Н.И.  Лобачквский Евклиддин V постулаты (параллелдик аксиомасы) калган аксиомалардан көз каранды эмес экендигин далилдеп, ошондой эле анны далилдөөгө мүмкүн эмес экендигин көрсөттү. Демек, Н.И.Лобачевскийдин ою боюнча, Евклиддин геометриясы бирден-бир мүмкүн болгон геометрия болуп эсептелбейт, башка да геометриялар болушу мүмкүн. Ошентип,  профессор В.Ф.Кагандын (1869-1953) сөзү боюнча: «Лобачевский геометриянын негизин   ширеп турган музду жарып талкалады».

            Н.И. Лобачевскийге чейин илим бир гана геометрияны билген. Азыркы убакта бизге белгилүү геометриялардын саны көбөйүүдө.

            в) Лобачевскийдин геометриясынын түзулүшү жалпы эле геометриянын түзүлүшүнө, ошону менен бирге математиканын негизделишине азыркы көз карашта болууга алып келди. Демек, Лобачевскийдин эмгеги азыркы математика үчүн мүнөздүү болгон аксиоматикалык методдун башталышын түздү. Аксиомалаштыруу маселеси математиканын башка областтарында да колдонула баштады.

            г) Лобачевскийдин идеялары Эйнштейндин (1879-1955, физик) салыштырмалуулук

теориясында, кванттык механикада, өтө чоң ылдамдыкка ээ болуучу кыймылдарды үйрөнүүдө, азыркы атомдук физикада, космос илиминде кеңири колдонула баштады жана колдонулуп жатат.