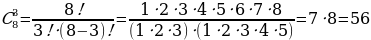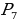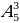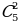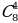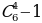Основные понятия комбинаторики.
Факториал числа – это произведение натуральных чисел от 1 до самого числа (включая данное число). Обозначается факториал восклицательным знаком n!
0! =1 1! = 1
Пример. Вычислить факториалы следующих чисел: 3! 5!
3! = 1·2·3 = 6 5! = 1·2·3·4·5 = 120
Комбинаторикой называют область математики, которая изучает вопросы о числе различных комбинаций (удовлетворяющих тем или иным условиям), которые можно составить из данных элементов.
(Комбинаторика – раздел математики, в котором исследуются и решаются задачи выбора элементов из исходного множества и расположения их в некоторой комбинации, составляемой по заданным правилам.)
Группы, составленные из каких-либо элементов, называются соединениями.
Различают три вида соединений: размещения, перестановки и сочетания.
Задачи, в которых производится подсчет возможных различных соединений, составленных из конечного числа элементов по некоторому правилу, называются комбинаторными, а раздел математики, занимающийся их решением, - комбинаторикой. Рассмотрим три основных вида соединений и формулы вычисления их количества. Для этого сначала рассмотрим 2 задачи, которые помогут нам сосредоточиться на сути новых понятий.
Размещения
Определение. Размещениями из m элементов по n элементов
( n ≤ m ) называются такие соединения, каждое из которых содержит n элементов, взятых из m данных разных элементов, и которые отличаются одно от другого либо самими элементами, либо порядком их расположения
Число размещений из m элементов по n обозначают  (от французского «arrangement» - «размещение») и вычисляют по формуле:
(от французского «arrangement» - «размещение») и вычисляют по формуле: 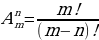
Пример 1. 
Пример 2. 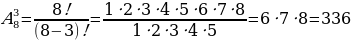
Перестановки
Определение. Перестановкой из n элементов называют размещение из n элементов по n.
Число перестановок из n элементов обозначается  и вычисляется по формуле:
и вычисляется по формуле: 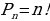
Сочетания
Определение.
Сочетаниями из m элементов по n элементов ( n ≤ m ) называются такие соединения, каждое из которых содержит n элементов, взятых из m данных элементов, и которые отличаются друг от друга по крайней мере одним элементом.
Число сочетаний из n элементов по m обозначают  (от французского «combination» - «сочетание») и вычисляют по формуле:
(от французского «combination» - «сочетание») и вычисляют по формуле: 
Пример 3. 
Пример 4. 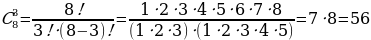
При решении комбинаторных задач важно научиться различать виды соединений.
| Перестановки из n элементов | Пример: Сколькими способами можно с помощью букв A, B, C, D обозначить вершины четырехугольника? | Меняется только порядок расположения выбранных элементов |
| Сочетания из m элементов по n элементов | Пример: У лесника три собаки: Астра, Вега и Граф. На охоту лесник решил пойти с двумя собаками. Перечислите все варианты выбора лесником пары собак. | Меняется только состав входящих в комбинацию элементов, порядок их расположения не важен |
| Размещения из m элементов по n элементов | Пример: Сколькими способами могут быть распределены I, II и III премии между 15-ю участниками конкурса? | Меняется состав входящих в комбинацию элементов и важен порядок их расположения |
Закрепление материала
Задание: выполнить вычисления ниже таблицы, а в таблицу записать только ответы (без заданий)







 (от французского «arrangement» - «размещение») и вычисляют по формуле:
(от французского «arrangement» - «размещение») и вычисляют по формуле: 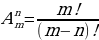

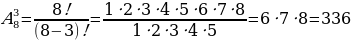
 и вычисляется по формуле:
и вычисляется по формуле: 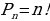
 (от французского «combination» - «сочетание») и вычисляют по формуле:
(от французского «combination» - «сочетание») и вычисляют по формуле: