Выполнили:
Переходько И.А, Здоров А.А
Научный руководитель: Шнарева Г.В
Прибрежненский аграрный колледж
Отделение механизации, электрификации и компьютеризации АПК
Тема доклада: Особенности поддержки принятия управленческих решений в математическом пакете Mathcad: исследование функции
Для принятия управленческих решений экономист использует функции, которые находят широкое применение в экономической теории и практике. Спектр используемых функций весьма широк: от простейших линейных до функций, получаемых по определенному алгоритму с помощью рекуррентных соотношений, связывающих состояния изучаемых объектов в разные периоды времени.
Учитывая, что экономические явления и процессы обусловлены действиями различных факторов, для их исследования широкого используются функции многих переменных. Если действием побочных факторов можно пренебречь, или удается зафиксировать эти факторы на определенных уровнях, то зависимость одного основного фактора изучается с помощью функции одной переменной.
Наиболее часто используются в экономике следующие функции:
1. Функция полезности (функция предпочтения).
2. Производственная функция.
3. Функция выпуска.
4. Функция издержек.
5. Функция спроса, потребления и предложения.
Функции в экономике позволяют количественно проанализировать важнейшие экономические зависимости, в частности в сфере производства. Они дают возможность оценить среднюю и предельную эффективность различных ресурсов производства, эластичность выпуска по различным ресурсам, предельные нормы замещения ресурсов, эффект от масштаба производства и многое другое.
Из этого следует, что экономисту необходимо обладать навыками полного исследования функции.
Автоматизировать процесс исследования функции можно с помощью математических пакетов, таких как: Derive, Mathematica, MapleV, MathCad.
MathCAD - универсальный математический пакет, предназначенный для выполнения инженерных и научных расчетов.
Он остается единственной системой, в которой описание решения задач задается с помощью привычных математических формул и знаков.
Достоинства Mathcad:
удобный для описания аналитических моделей дружественный интерфейс, ориентированный на классическую форму языка математики. Программа, в отличие, например, от MathLab’а, достаточно проста в освоении для того, чтобы ее применяли не только ученые, инженеры или студенты вуза, но и школьники старших классов. Как калькулятор в свое время упростил изучение арифметики в школе, так и Mathcad может позволить упростить освоение школьниками алгебры и геометрии, да и математического аппарата школьной физики;
возможность не только численного, но и символьного решения многих задач. Последнее особенно впечатляет: программа аналитически определяет значения производных, сумм и интегралов, упрощает аналитические выражения и т.п.
наличие интерактивного учебника и множества шаблонов для решения типовых задач математики, физики, техники, бизнеса и др.
Возможность вставки документа Mathcad в другое приложение, например, в VisSim, который будет обмениваться информацией с программой Mathcad, и использовать его вычислительно-аналитические ресурсы в процессе моделирования. Однако если сравнить VisSim со скакуном, то Mathcad в таком случае можно приравнять к плугу: вставка элемента программы Mathcad в VisSim существенно тормозит работу последнего. Во многих случаях моделирования это не критично, а совокупная вычислительная мощность упрощает работу исследователя и делает ее более эффективной.
Наличие встроенного языка программирования. С одной стороны, это вынужденная мера, поскольку разработчики не могут предвосхитить и обеспечить все потенциальные требования пользователей.
В данном исследовании был выбран математический пакет MathCad, так как он имеет простой пользовательский интерфейс, удобный для работы с изучением функции. Так же MathCad является универсальным помощником в решении сложных задач.
Для полного исследования функции используется определенная схема:
Найти область определения функции
Исследовать функцию на четность
Найти асимптоты функции
Найти интервалы монотонности и экстремум функции
Найти интервалы выпуклости точки перегиба функции
Найти точки пересечения с осями координат
Найти если необходимо дополнительные точки
Построить график функции
Все этапы исследования выполняются в MathCad следующим образом:
| Этапы исследования | Действия | Оператор |
| Задать функцию | f(x):= |
|
| Найти область определения функции, точки разрыва, определить четность (симметричность графика) | Для этого необходимо либо
определить ОДЗ самостоятельно, либо решить необходимые уравнения и неравенства. Для определения четности необходимо задать функцию относительно переменной (-x). Сделать вывод о четности функции самостоятельно и вывод о симметрии графика | f(-x)→ (→ находится на панели Вычисление) |
| Найти асимптоты графика функции | Найти предел функции для x→∞, x→a |  (находится на панелиИсчисление) (находится на панелиИсчисление)
|
| Найти точки экстремума функции | Найти производную функции, приравнять ее к нулю и найти стационарные точки. Определить, какая точка является точкой максимума, а которая минимума. Найти критические точки. | 
Minimize(f,x0)
Maximize(f,x0) |
| Найти промежутки монотонности | Решитьнеравенство D(x)0, D(x) | D1(x)0→solve,x
D1(x) |
| Найти точки перегиба и выпуклости | Найти вторую производную функции,приравнивать ее к нулю. И определить, являются ли эти точки точками перегиба, и интервалы вогнутости функции. | 
D2(x)0→solve,x
D2(x) |
| Найти точки пересечения с осями координат | Решить уравнение f=0 при x=0 и y=0 | F(0) Solve,x→ (→ на панели Символьная) |
| Построить график | С учетом всех полученных точек строим график функции | На панели график –X-Y график. |
Рассмотрим исследование функции на примере функции
выручки от реализации товара по цене р в математическом пакете MachCad.

- области определения
p0.
- функция имеет горизонтальную асимптоту у=0
- функция нечетная


На основе этого исследования функции можно сделать вывод:
Производная этой функции  положительна, если
положительна, если  и отрицательна для
и отрицательна для  , это означает, что с ростом цены выручка вначале увеличивается (несмотря на падение спроса) и
, это означает, что с ростом цены выручка вначале увеличивается (несмотря на падение спроса) и  достигает максимального значения
достигает максимального значения  , дальнейшее увеличение цены не имеет смысла, т.к. оно ведет к сокращению выручки.
, дальнейшее увеличение цены не имеет смысла, т.к. оно ведет к сокращению выручки.
Темп изменения выручки выражается второй производной 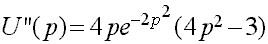 . При
. При 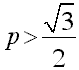 темп положительный, а при
темп положительный, а при  темп отрицательный.
темп отрицательный.
Сначала выручка возрастает с отрицательным темпом для  , а затем темп убывания становится положительным и для р0,9 выручка убывает все быстрее и приближается к нулю при неограниченном увеличении цены.
, а затем темп убывания становится положительным и для р0,9 выручка убывает все быстрее и приближается к нулю при неограниченном увеличении цены.
На промежутке а на функция U(p) вогнута. В точке  график перегибается.
график перегибается.
Таким образом, математический пакет MathCad является очень удобным инструментом для исследования функции.
Список литературы
Высшая математика для экономистов: учебник для студентов вузов, обучающихся по экономическим специальностям / [Н.Ш. Кремер и др.]; под ред. проф. Н.Ш. Кремера – 3-е изд. – М.:ЮНИТИ-ДАНА, 20072.
Черняк А. А., Новиков В. А., Мельников О. И., Кузнецов А. В.Математика для экономистов на базе MathCad. – СПб.: БХВ-Петербург, 2003. – 496 с: ил.
Малыхин В.И. Высшая математика: Учеб. пособие. — 2-е изд., перераб. и доп. — М.: ИНФРА-М, 2009. — 365 с. — (Высшее образова- ние).
О.О. Толстонятенко, А.В. Черемных, Ю.Н.Математические методы в экономике: Учебник. 2-е изд. – М.: МГУ им. М.В. Ломоносова, Издательство «Дело и Сервис», 2005. – 368 с.









 график перегибается.
график перегибается.









