"От Евклида до Лобачевского"

Региональный конкурс исследовательских и проектных работ

«Высший пилотаж»

Исследовательская работа

«От Евклида до Лобачевского»

Подготовил: Помогалов Иван Сергеевич,

учащийся 11 класса,

Муниципальное общеобразовательное

учреждение Новохоперского муниципального района Воронежской области "Елань - Коленовская СОШ №1", село Елань-Колено

Руководитель: Морозова Светлана Владимировна, учитель математики,

Муниципальное общеобразовательное

учреждение Новохоперского муниципального района Воронежской области "Елань - Коленовская СОШ №1", село Елань-Колено

2021 год

СОДЕРЖАНИЕ

Введение…………………………………………………………………………..2

Глава 1. Евклидова геометрия

1.1 «Начала» Евклида и пятый постулат………………………………………..4

1.2 Эквиваленты пятого постулата Евклида……………………………………6

Глава 2. Становление неевклидовой геометрии

2.1 Предшественники неевклидовой геометрии……………………………….9

2.2 Основоположники первой неевклидовой геометрии……………………..11

2.3 Эллиптическая геометрия Римана………………………………………….13

2.4 Похожие, но такие разные…………………………………………………..14

Заключение……………………………………………………………………….15

Литература………………………………………………………………………..16

Во всей истории науки нет ничего более революционного, чем развитие неевклидовых геометрий, которое до основания потрясло веру в то, что теория Евклида является вечной истиной

Эдвард Каснер и Джеймс Ньюмен

(«Математика и воображение», 1941)

Геометрия – это одна из наиболее древних математических наук. Первые геометрические факты найдены в вавилонских клинописных таблицах и египетских папирусах (3 тысячелетие до н.э.). Возникновение геометрических знаний связано с практической деятельностью человека. Все мы знаем множество геометрических понятий, потому что постоянно используем этот раздел математики в нашей повседневной жизни. Но эти понятия относятся к так называемой «классической», или «евклидовой», геометрии. Однако же существуют и другие геометрии, которые устроены совсем не так, как нас учат в школе.

Первоначально геометрия была наукой об измерениях. Греческие геометры умели измерять отрезки линий (как прямых, так и кривых), площадь поверхности, ограниченной линиями, и объемы фигур, ограниченных поверхностями. Однако глагол «измерять» вскоре принял более широкий смысл: «устанавливать отношения между геометрическими объектами». Появились геометрические формулировки, которые используются и сегодня: «прямая линия а параллельна прямой b» отрезок АC в три раза длиннее отрезка АВ», «отношение периметра окружности к ее диаметру есть число, которое не может быть выражено в виде дроби».

Для установления истинности таких отношений геометры древности разработали и довели до совершенства особую систему доказательств, которая стала основным методом математики. Эта система состояла в выводе важнейших результатов (теорем) из набора основополагающих аксиом с помощью «длинных цепочек рассуждений». Этот подход является характерной чертой евклидовой геометрии.

На протяжении столетий работы Евклида, в частности его пятый постулат, вызывали многочисленные комментарии и критику самых известных геометров. Многие из них были убеждены, что пятый постулат можно доказать с помощью других постулатов, и сосредоточили свои усилия на поиске такого доказательства, чтобы, наконец, объявить его теоремой.

Проблема: чем занималось человечество от Евклида до Лобачевского?

Объект исследования: попытки доказательства пятого постулата Евклида.

Цель моей работы: выяснить причину разделения геометрии на классическую (евклидову) и неевклидову геометрию, узнать каким образом на это повлиял пятый постулат.

Задачи:

1. Собрать исторический материал о Евклиде и «Началах»;

2. Узнать подробнее о пятом постулате;

3. Узнать имена ученых, занимавшихся его доказательством;

4. Узнать удалось ли решить проблему с этой теоремой;

5. Выяснить какие геометрии являются неевклидовыми и чем они различаются.

В ходе моей работы над проектом я предполагаю проверить гипотезу: от Евклида и до Лобачевского существовало огромное количество иных ученых, которые смогли опровергнуть или подтвердить пятый постулат, вывести свой, эквивалентный евклидову.

Глава 1. Евклидова геометрия

1. «Начала» Евклида и пятый постулат

Е вклид или Эвклид (др.-греч. Εὐκλείδης, от «добрая слава», время расцвета — ок. 300 г. до н. э.) – древнегреческий математик, автор первого из дошедших до нас теоретических трактатов по математике. Биографические сведения о Евклиде крайне скудны. Достоверным можно считать лишь то, что его научная деятельность протекала в Александрии в III в. до н.э.

Евклид написал свой великий труд «Начала», содержащий практически все известные в то время математические сведения. Она на протяжении почти 2000 лет использовалась в качестве учебного пособия и считалась нерушимой основой не только геометрии, но и здравого смысла. Первая печатная версия «Начал» появилась в Венеции в 1482 г. (это был перевод с арабского языка на латинский). Первая же версия прямого перевода с греческого на латынь была опубликована в 1505 г.

Первое издание «Начал» на русском языке издано в 1739 году; книга вышла в Петербурге под названием «Евклидовы элементы из двенадцати нефтоновых книг выбранныя и в осьмь книг через профессора мафематики Андрея Фархварсона сокращенныя, с латинского на российский язык хирургусом Иваном Сатаровым преложенныя». Перевод выполнил Иван Сатаров под руководством шотландского математика Генри Фарварсона, служившего в это время при российском Морском корпусе. Имя Ньютона («Нефтона») в названии упомянуто то ли по недоразумению, то ли в рекламных целях, к содержанию книги он никакого отношения не имеет. Перевод был сделан с сокращённого и модернизированного французского издания «Начал» Андре Таке, куда переводчиками были добавлены ряд числовых примеров и критические комментарии.

«Начала геометрии» (или «Начала») состоят из 13 книг, содержащих 465 утверждений, 372 теоремы и 93 задачи.  В книге I рас­смат­ри­ва­ют­ся основные свой­ст­ва тре­уголь­ни­ков, пря­мо­уголь­ни­ков, па­рал­ле­ло­грам­мов и про­из­во­дит­ся срав­не­ние их пло­ща­дей. Кни­га за­кан­чи­ва­ет­ся Пи­фа­го­ра тео­ре­мой. В книге II из­ла­га­ет­ся так называемая гео­мет­рическая ал­геб­ра, то есть стро­ит­ся гео­мет­рический ап­па­рат для ре­ше­ния за­дач, сво­дя­щих­ся к квад­рат­ным урав­не­ни­ям. В книге III рас­смат­ри­ва­ют­ся свой­ст­ва кру­га, его ка­са­тель­ных и хорд. В книге IV - пра­виль­ные мно­го­уголь­ни­ки. В книге V да­ёт­ся об­щая тео­рия про­пор­ций, соз­дан­ная Ев­док­сом Книд­ским; её мож­но рас­смат­ри­вать как про­об­раз тео­рии дей­ст­ви­тель­ных чи­сел, раз­ра­бо­тан­ной во второй половине XIX века. Об­щая тео­рия про­пор­ций яв­ля­ет­ся ос­но­вой уче­ния о по­до­бии (книга VI) и ме­то­да ис­чер­пы­ва­ния (книга VII). В кни­гах VII-IX из­ло­же­ны на­ча­ла тео­рии чи­сел, ос­но­ван­ные на ал­го­рит­ме на­хо­ж­де­ния наи­боль­ше­го об­ще­го де­ли­те­ля (Евк­ли­да ал­го­ритм). В книге Х да­ёт­ся клас­си­фи­ка­ция квад­ра­тич­ных и би­квад­ра­тич­ных ир­ра­цио­наль­но­стей и обос­но­вы­ва­ют­ся не­ко­то­рые пра­ви­ла их пре­об­ра­зо­ва­ния. Ре­зуль­та­ты книги Х при­ме­ня­ют­ся в книге XIII для на­хо­ж­де­ния длин рё­бер пра­виль­ных мно­го­гран­ни­ков. В книге XI из­ла­га­ют­ся ос­но­вы сте­рео­мет­рии. В книге XII с по­мо­щью ме­то­да ис­чер­пы­ва­ния оп­ре­де­ля­ют­ся от­но­ше­ния пло­ща­дей двух кру­гов и от­но­ше­ния объ­ё­мов пи­ра­ми­ды и приз­мы, ко­ну­са и ци­лин­д­ра. В книге XIII оп­ре­де­ля­ет­ся от­но­ше­ние объ­ё­мов двух ша­ров, стро­ят­ся 5 пра­виль­ных мно­го­гран­ни­ков и до­ка­зы­ва­ет­ся, что др. пра­виль­ных мно­го­гран­ни­ков не су­ще­ству­ет. Позд­нее греческими ма­те­ма­ти­ка­ми к ««Началам» Евклида бы­ли при­сое­ди­не­ны кни­ги XIV и XV, не при­над­ле­жав­шие Евк­ли­ду.

« Начала» Евклида по­строе­ны по де­дук­тив­ной сис­те­ме: сна­ча­ла при­во­дят­ся оп­ре­де­ле­ния, по­сту­ла­ты и ак­сио­мы, за­тем фор­му­ли­ров­ки тео­рем и их до­ка­за­тель­ст­ва. Вслед за оп­ре­де­ле­ни­ем ос­нов­ных гео­мет­рических по­ня­тий и объ­ек­тов (например, точ­ки, пря­мой) Евк­лид до­ка­зы­ва­ет су­ще­ст­во­ва­ние ос­таль­ных объ­ек­тов гео­мет­рии (например, рав­но­сто­рон­не­го тре­уголь­ни­ка) пу­тём их по­строе­ния, ко­то­рое вы­пол­ня­ет­ся на ос­но­ва­нии пя­ти по­сту­ла­тов:

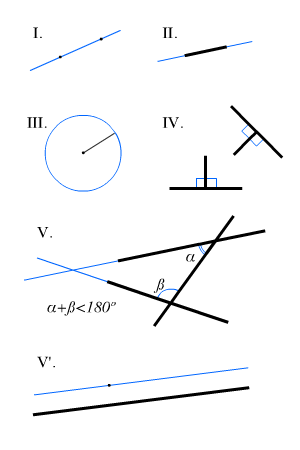
1. От вся­кой точ­ки до вся­кой точ­ки (мож­но) про­вес­ти пря­мую ли­нию.

2. Любой отрезок можно непрерывно продолжать по прямой линии.

3. От вся­ко­го цен­тра и вся­ким рас­тво­ром (мо­жет быть) опи­сан круг.

4. Все прямые углы равны между собой

5. Если две прямые пересекаются третьей, так что с одной стороны сумма внутренних углов меньше двух прямых углов меньше двух прямых углов, то эти две прямые неизбежно пересекаются друг с другом по эту сторону, будучи продленными достаточно далеко.

По­сле по­сту­ла­тов в «Началах» Евклида при­во­дят­ся ак­сио­мы - пред­ло­же­ния о свой­ст­вах от­но­ше­ний ра­вен­ст­ва и не­ра­вен­ст­ва ме­ж­ду ве­ли­чи­на­ми. Евклид первым поставил задачу обоснования геометрии, т.е. перечисления определений и аксиом, на основе которых можно развивать геометрию строго логическим путем. В этом его историческая заслуга перед наукой. Логическое построение геометрии было проведено Евклидом для его времени чрезвычайно точно. Но, с точки зрения современной математики, изложение «Начал» надо признать неудовлетворительным. Данные в первой книге определения геометрических объектов являются скорее описанием их, причем далеко не совершенным. Так, например, определение прямой линии содержит упоминание о длине и ширине, которые сами нуждаются в определении. Целый ряд определений, в том числе окружности, треугольника, прямого, острого и тупого угла, либо безупречны, либо содержат легко устранимые недостатки. Если при этом учесть, что свойства геометрических объектов, содержащиеся в дефектных определениях, нигде в доказательствах не используются, то эти определения могут быть опущены без ущерба для изложения.

1.2 Эквиваленты пятого постулата Евклида

Но логическое построение «Начал», аксиоматика Евклида воспринималась математиками как безупречное вплоть до 19 века, когда начался период критического отношения к достигнутому.

Одним из ученых, работавших над проблемой пятого постулата, был профессор Оксфордского университета Джон Валлис (1636-1703). Он считал бесспорным следующее положение: «Для каждой фигуры всегда существует подобная ей фигура произвольной величины» - и в 1663г. на основании этой аксиомы изложил «доказательство» V постулата Евклида. На самом деле аксиома Валлиса о существовании подобных фигур эквивалентна V постулату («забегая вперед», скажем, что в геометрии Лобачевского подобные треугольники не существуют).

П остулат Джона Плейфера (1748-1819): «Через точку C, лежащую вне прямой AB, в плоскости ABC проходит только одна прямая, не встречающая AB» или «В плоскости через точку, не лежащую на данной прямой, можно провести одну и только одну прямую параллельную данной». Нужно сказать, что эта формулировка встречалась у различных авторов до Плейфера.

Очень распространена также еще следующая формулировка, связываемая с именем Лежандра.

П остулат Адриена Мари Лежандра (1752-1833): «Перпендикуляр и наклонная к общей секущей, расположенные в одной плоскости, необходимо встречаются (конечно, с той стороны секущей, с которой наклонная образует с секущей острый угол)».

Более 40 лет он искал доказательство пятого постулата, которое было бы математически строгим, но и в то же время понятным. К сожалению, он умер, так и не увидев развития неевклидовых геометрий. Однако именно он сформулировал постулат для углов треугольника: «Существует треугольник, сумма углов которого равна двум прямым».

К арл Фридрих Гаусс (1777-1855) обратился к теории параллельных в 1792 г. Сначала он надеялся доказать пятый постулат, но затем пришел к мысли о построении новой геометрии, которую назвал неевклидовой. В 1817 г. в одном из писем признался: "Я прихожу все более к убеждению, что необходимость нашей геометрии не может быть доказана". Но обнародовать эти идеи он не решился из боязни быть непонятым. Гаусс не опубликовал ни один из своих результатов, хотя из его писем и личных бумаг видно, что он разработал основные положения неевклидовой геометрии. После смерти Гаусса в его бумагах были найдены наброски отдельных наиболее простых теорем гиперболической геометрии. Гаусс сформулировал постулат о площади треугольника: «Существует треугольник сколь угодно большой площади».

Творцом новой геометрии стал так же и венгерский математик Янош Бойяи (1802 - 1860). В отличие от Гаусса он стремился распространить свои идеи, но большинство математиков тогда еще не были готовы их воспринять. Его постулат о трех точках: «Через любые три точки, не лежащие на прямой линии, всегда можно провести окружность». Результаты Яноша Больяя были сжато изложены в 1832 г. в приложении книге его отца, Фаркаша Бойяя. Труд Я. Бойяя "Приложение, содержащее науку о пространстве, абсолютно истинную, не зависящую от истинности или ложности XI аксиомы Евклида (что a priori никогда решено быть не может)" обычно кратко называют "Аппендикс" (от лат. "приложение"). В этой работе, составившей приложение к математическому трактату его отца Фаркаша Бойяи, Янош Бойяи изложил ту же теорию, что и Лобачевский, но в значительно менее развитой форме. Не найдя поддержки у современников, Я. Бойяйи перестал заниматься математикой. Он умер в состоянии глубокой депрессии за несколько лет до того, как неевклидова геометрия получила всеобщее признание.

После многих столетий развития математических теорий никто так и не смог доказать ни сам постулат, ни ложность тех геометрий, которые этот постулат отвергают.

Глава 2. Становление неевклидовой геометрии

2.1 Предшественники неевклидовой геометрии

Д жироламо Саккери (1667 - 1733) - итальянский математик, иезуит, создатель первого наброска неевклидовой геометрии. Он как и многие другие математики пытался доказать пятый постулат, в своей работе он воспользовался методом доказательства от противного. Он даже подумал, что ему удалось доказать постулат, но потом он понял, что так и не получил убедительного противоречия.

Его работа неявно предполагает существование других геометрий, которые возникают именно из-за невозможности достижения противоречия, исходя из предположения о ложности пятого постулата. Сам не осознавая того, Саккери создал новую геометрию, в которой пятый постулат заменен противоположным ему утверждением.

Саккери рассмотрел четырехугольник, у которого две стороны конгруэнтны, а пара углов прилежащих к этим сторонам прямые. Он выдвинул три гипотезы:

1. Гипотеза о прямых углах: углы В и С являются прямыми.

2. Гипотеза о тупых углах: углы В и С являются тупыми, то есть их величина больше 90° и меньше 180°.

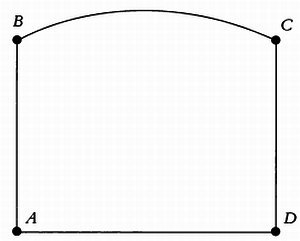
3. Гипотеза об острых углах: углы В и С являются острыми, то есть их величина больше 0° и меньше 90°.

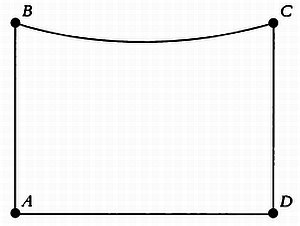
Четырехугольники такого вида называют теперь «четырехугольниками Саккери».

Саккери показал, что гипотеза о прямых углах эквивалентна пятому постулату, а затем попытался доказать, что другие гипотезы приводят к противоречию. Если бы ему это удалось, то постулат был бы доказан. Рассматривая вторую гипотезу (случай тупых углов), он получил противоречие и отбросил эту возможность. Но для гипотезы острых углов ему не удалось получить противоречия. Теперь-то мы точно знаем, что противоречия не существует, и гипотеза об острых углах является одной из основ неевклидовой геометрии

Исходя из гипотезы об острых углах, Саккери получил различные результаты неевклидовой геометрии. Он открыл тот факт, что в случае гипотезы острого угла геометрическое место точек, равноудаленных от данной прямой, есть кривая. В наше время эта геометрия известна как гиперболическая.

Достижения итальянского математика велики, но, к сожалению, ему не хватило смелости, в своем трактате он пишет: «Гипотеза об острых углах является абсолютно ложной, поскольку противоречит самому понятию прямой линии».

Казалось, что задача о параллельных прямых останется нерешенной еще многие годы.

В XVIII веке была посмертно издана книга швейцарского математика Иоганна Генриха Ламберта (1728-1777) «Теория параллельных» (1786), в которой он высказал ряд глубоких мыслей о роли «пятого постулата» в геометрии. Он составил список нескольких утверждений, которые должны быть доказаны, среди них – и пятый постулат. В последней главе своей книги он рассматривал четырехугольники с тремя прямыми углами (А, В и D). Для четвертого угла снова было три возможности. Четырехугольником Ламберта называют такой четырехугольник ABCD, у которого углы А, В и D прямые, а угол С не равен 90°.

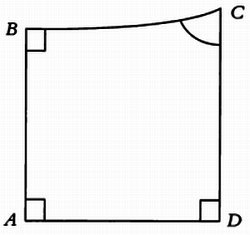
Ни Саккери, ни Ламберт так и не смогли найти неопровержимого доказательства того, что пятый постулат невозможно доказать. Все последующие попытки доказательства всегда возвращались к исходной точке и приводили математиков к понятиям неевклидовой геометрии.

2.2 Основоположники первой неевклидовой геометрии

Вообще, в течение первых же десятилетий XIX века проблема V постулата была решена несколькими лицами почти одновременно и независимо друг от друга, но совершенно не так, как предлагали это прежние ученые: была создана новая геометрия, не зависимая от V постулата, основанная на замене его утверждением, эквивалентным гипотезе острого угла Саккери.

Итак, благодаря проблеме пятого постулата, человечество подошло к новому крутому повороту в своей истории, который дал толчок к зарождению и развитию новых, неевклидовых геометрий, а вместе с тем новый виток развития получил и весь научный мир. К открытию новой, к так называемой «неевклидовой» геометрии (гиперболической геометрии) пришли три человека:

1) Карл Фридрих Гаусс (1777 – 1855) – великий немецкий математик;

2) Янош Бойяи (1802 – 1860) – венгерский офицер, сын Фаркаша Бойяи.

3) Николай Иванович Лобачевский (1792 – 1856) – профессор Казанского университета.

Однако вклад в создание новой геометрии, внесенный этими учеными, весьма неравноценен. Что касается Гаусса, то он совершенно не оставил никаких следов систематического изложения своих открытий в области неевклидовой геометрии и при жизни не опубликовал ни строчки по этому вопросу. То, что Гаусс владел идеями неевклидовой геометрии, было обнаружено лишь после смерти ученого, когда стали изучать его архивы. Гениальный Гаусс, к мнению которого все прислушивались, не рискнул опубликовать свои результаты по неевклидовой геометрии, опасаясь быть непонятым и втянутым в полемику.

Янош Бойяи пришел к открытию неевклидовой геометрии в 1823 году, будучи в возрасте 21 года, но опубликовал свои результаты в 1832 году, позже Лобачевского.

Все, сделанное в области геометрии Гауссом и Я. Бойяи, представляет собой лишь первые шаги по сравнению с глубокими и далеко идущими исследованиями Лобачевского, который всю жизнь упорно и настойчиво разрабатывал с разных точек зрения свое учение, довел его до высокой степени совершенства и опубликовал целый ряд крупных сочинений по новой геометрии.

Потому первое место среди лиц, разделяющих славу создания неевклидовой геометрии, следует безраздельно отвести Лобачевскому, имя которого и носит созданная им геометрия.

В ней сохраняются все теоремы, которые в евклидовой геометрии можно доказать без использования V постулата (или аксиомы параллельности – одного из эквивалентов V постулата, - включенной в наши дни в школьные учебники).

Теорема о сумме углов треугольника – первая теорема школьного курса, при доказательстве которой используется аксиома параллельности. Здесь нас ожидает первый «сюрприз»: в геометрии Лобачевского сумма углов любого треугольника меньше 180⁰. Теоремы о признаках подобия треугольников говорят нам об их существовании в евклидовой геометрии. В неевклидовой геометрии, то есть в геометрии Лобачевского, подобных треугольников не существует. Здесь мы получаем второй «сюрприз». Если два угла одного треугольника равны двум углам другого треугольника, то в евклидовой геометрии равны и третьи углы (тогда треугольники подобны), но в геометрии Лобачевского это не всегда верно. Более того, имеет место четвертый признак равенства треугольников: если углы одного треугольника соответственно равны углам другого треугольника, то эти треугольники равны.

Таким образом, мы получаем «чудовищные» противоречия с нашими геометрическими взглядами, но не видим никаких логических противоречий.

2.3 Эллиптическая геометрия Римана

Вскоре после того как была построена новая геометрия Лобачевского и Бойяи, появилась другая неевклидова геометрия. Ее создал известный немецкий математик Бернхард Риман (1826-1866)

Геометрия Римана, также носит название «эллиптическая геометрия». Если геометрия Евклида реализуется в пространстве с нулевой гауссовой кривизной, Лобачевского - с отрицательной, то геометрия Римана реализуется в пространстве с постоянной положительной кривизной (в двумерном случае — на проективной плоскости и локально на сфере).

В геометрии Римана прямая определяется двумя точками, плоскость — тремя, две плоскости пересекаются по прямой и т. д., но в его геометрии нет параллельных прямых.

Д вумерная геометрия Римана похожа на сферическую геометрию, но отличается тем, что любые две «прямые» имеют не две, как в сферической, а только одну точку пересечения. При отождествлении противоположных точек сферы получается проективная плоскость, геометрия которой удовлетворяет аксиомам геометрии Римана.

Чтобы лучше понять геометрию Римана, можно провести несложный эксперимент с воздушным шариком. На надутом воздушном шарике прямая превращается в кривую, называемую геодезической линией, которая является большим кругом на сфере. Риман не мог провести этот простой, но наглядный эксперимент. В его время воздушные шарики еще не были изобретены.

Риман прокомментировал книгу Лобачевского «Новые начала геометрии»: «Евклид утверждал, что через точку вне данной прямой можно провести только одну параллельную ей линию, Лобачевский писал, что параллельных ей линий можно провести сколько угодно, а я говорю, что нельзя провести ни одной»

2.4 Похожие, но такие разные

Первыми математиками, которые разделили все геометрии на три типа, были Феликс Клейн и основатель современной британской школы чистой математики Артур Кэли (1821–1895). Выделив гиперболическую и эллиптическую геометрии, они описали евклидову геометрию как параболическую.

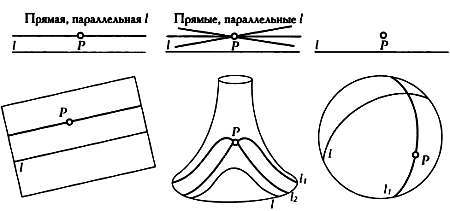
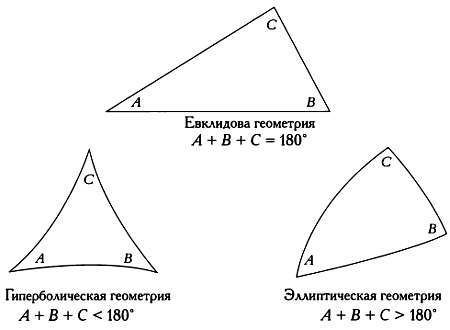
В таблице приведены основные различия этих геометрий

Параллельные прямые, треугольники и четырехугольники в различных геометриях:

Заключение

В своей исследовательской работе я ответил на все поставленные мною вопросы, прочитал литературу, познакомился с некоторыми доказательствами пятого постулата, понял, что все попытки доказать его были безуспешны, т. к. в процессе доказательства применялись элементы теории параллельности Евклида. Узнал, почему геометрия разделилась на евклидову и абсолютную геометрию, и то, что пятый постулат сыграл большую роль и стал отправной точкой для разделения геометрии.

В дальнейшем мне хотелось бы более подробно узнать о гиперболической и эллиптической геометриях, о том, как развивались эти геометрии, как и где они применяются в наше время. Наверняка, существуют еще какие-то геометрии, с которыми мне еще не доводилось встретиться и, которые такие же интересные и необычные для нашего восприятия.

Список литературы

1. Мир математики: в 40 т. Т.4: Жуан Гомес. Когда прямые искривляются. Неевклидовы геометрии./ Пер.с англ. – М.: Де Агостини, 2014. - 160 с.

2. Энциклопедический словарь юного математика / сост. А.П. Савин. М.: Педагогика. 1998.

3. Силин А.В., Шмакова Н.А. Открываем неевклидову геометрию. Кн. Для внеклас. чтения учащихся 9-10 кл. сред. шк.—М.: Просвещение, 1988.

4. Юшкевич А. П. О первом русском издании трудов Эвклида и Архимеда // Труды Института истории естествознания и техники. - М.: Академия наук СССР, 1948. - Вып. 2.

5. https://ru.wikipedia.org/wiki/%D0%9D%D0%B0%D1%87%D0%B0%D0%BB%D0%B0_(%D0%95%D0%B2%D0%BA%D0%BB%D0%B8%D0%B4)

6. http://www.people.su/20124

7. https://www.liveinternet.ru/users/4373400/post233326198/

8. https://spacegid.com/biografiya-karla-gaussa.html

9. https://www.liveinternet.ru/users/4373400/post379511505/