Оглавление
I. Введение 3
II. Основная часть 5
1. Математические забавы 5
2. Комбинаторные игры 10
3. Теория игр 13
4. Применение теории игр к решению жизненных задач,
выигрышные стратегии 16
III. Заключение 19
IV. Список используемых источников 20
I. Введение
В наше время существует много вариантов проведения досуга, начиная с самого простого и привычного — просмотра телевизионных передач, занятий спортом, посещения музеев, театров, других объектов культуры и заканчивая наиболее “времяпоглощающим” занятием — Интернетом. Я задалась вопросом: “А как проводили время наши предки, когда у них не было ни телевизоров, ни радио, ни кино, ни тем более Интернета?”. Что могло их развлечь? Исследуя эту проблему, я выяснила, что с давних пор математики, а позднее и информатики занимаются изучением игр. Речь, конечно, идет не о компьютерных играх, и не о футболе, а об играх математических. Оказывается, есть даже теория игр, согласно которой принятие решения можно описать с помощью математических формул и законов.
Актуальность исследования заключается в том, что всю свою жизнь нам приходится принимать решения подобно игроку, пытаясь добиться максимально хорошего результата. Возможно, если бы мы лучше знали теорию, которая игровые явления обрабатывает математическим аппаратом, положительных результатов было бы больше.
Проблема исследования: как найти выигрышную стратегию, то есть – как играть, чтобы выиграть.
Объект исследования: математические игры.
Предмет исследования: выигрышные стратегии.
Гипотеза: предполагаю, что основой большинства выигрышных стратегий является хорошее владение математической наукой.
Цели: узнать что такое теория игр; изучить выигрышные стратегии; определить, каким образом принятие решений можно объяснить с точки зрения точных наук.
Задачи:
- изучить историю возникновения математических задач;
- познакомиться с комбинаторными задачами;
- изучить, что такое теория игр, и каковы её элементы;
- понять, как применить теорию игр в жизни.
Методы исследования:
- изучение учебной, научно-популярной литературы;
- поиск информации в сети Интернет;
- анализ полученной информации;
- практическое применение полученных знаний.
II. Основная часть
1. Математические забавы

Начать свой рассказ я хочу с математических фокусов, которые раньше были более популярны, нежели сейчас. Так как образование в настоящее время находится на гораздо более высоком уровне и является обязательным для каждого гражданина нашей страны, то понятно, что во времена Петра I и даже М.Ю. Лермонтова, о которых речь пойдет дальше, математические фокусы производили большее впечатление, а людям, их демонстрирующим, приписывались магические способности. Вначале мне хочется рассказать о Леонтии Филипповиче Магницком (рис.1) — авторе первого учебника по математике, вышедшего в России в 1703 г.
Рис.1. Л.Ф.Магницкий
Книга эта содержит начала математических знаний того времени: арифметики, алгебры, геометрии и тригонометрии. В конце книги имеется снабженный большим числом таблиц раздел, посвященный морскому делу. Большую часть места, как указывает и заглавие книги, автор посвящает арифметике. В царствование Петра I, когда вышла в свет книга, в России происходил быстрый рост промышленности и торговли, переворот в военной технике. Стране потребовались образованные люди в значительно большем количестве, чем в предшествующие десятилетия. Был создан ряд технических учебных заведений, первым из которых была “школа навигацких и математических наук”, открытая в Москве в Сухаревой башне в 1701 г. Учащимся в ней в первую очередь и предназначалась книга Магницкого. В течение полустолетия “Арифметика” с честью выполняла свою роль, став пособием для всех русских людей, которые стремились к математическому образованию. Об авторе этой замечательной книги мы знаем очень немного. Леонтий Филиппович Магницкий (Телятин) родился 9 июня 1669 года, умер в 1739 году. Надгробная надпись на могиле Магницкого, сделанная его сыном, рассказывает, что “Петр I многократно беседовал с ним о математических науках и был так восхищен глубокими п
ознаниями его, что называл его магнитом и приказал писаться Магницким (имея в виду его способность притягивать знания подобно магниту)”.
Рис.2
“Какое он имел прозвище до этого, то даже ближним его не известно”, — читаем в раннем его жизнеописании.
В “Арифметике” Магницкого (рис.3) есть особый раздел “О утешных неких действах, чрез арифметику употребляемых”, начинающихся с указания, что, следуя примеру арифметиков, автор помещает его в свою книгу для утехи и особенно для изощрения ума учащихся, хотя эти забавы, по его мнению, “и не зело нужные”. Уверена, что перевод последнего текста на современный русский язык не требуется. Замечу лишь, что Магницкий употребляет не очень привычное нам слово “забава” (развлечение, игра), которое будем использовать и мы.
П ервая забава
ервая забава
Один из находящихся в компании восьми человек берет кольцо и надевает на один из пальцев на определенную фалангу. Требуется угадать, у кого, на каком пальце и на какой фаланге находится кольцо.
Показывающий фокус просит участников произвести следующие действия:
1) присвоить каждому человеку условный номер (от 1 до 8);
2) пронумеровать пальцы (от 1 до 10);
3) пронумеровать фаланги пальцев (от 1 до 3);
Рис.3. Арифметика
Магницкого 4) номер человека, у которого находится кольцо,
удвоить;
5) к полученному результату прибавить 5;
6) умножить полученный результат на 5;
7) прибавить номер пальца;
8) приписать 0 к полученному числу справа;
9) прибавить номер фаланги;
10) вычесть 250.
По названному участниками полученному результату отгадывающий может определить все, что нужно.
Секрет забавы
Пусть номер человека, у которого находится кольцо, — а, номер пальца —в, номер фаланги —с.
Выполним действия 4–10 в общем виде:
а× 2 = 2а
2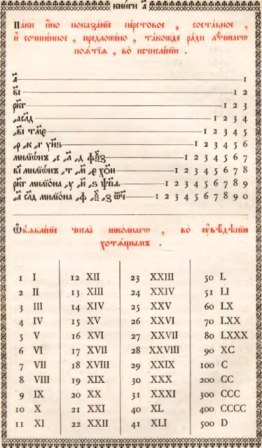 а+ 5
а+ 5
(2а+ 5) × 5 = 10а+ 25
10а+ 25 + в= 10а+в+ 25
(10а+в+ 25) × 10 == 100а+ 10в+ 250
100а+ 10в+ 250 +с= 100а+ 10в + с+ 250
100а+ 10в + с+ 250 – 250 = 100а+ 10в + с
В полученном числе:
цифра сотен — номер человека;
цифра десятков — номер пальца;
цифра единиц — номер фаланги.
Конечно, для произведения нужного эффекта необходимы актерские данные. Но все, что необходимо для отгадывания, называют сами зрители в конце фокуса.
Рис.4
Вторая забава
Пронумеруем дни недели, начиная с воскресенья: первый, второй и так далее до седьмого (до субботы). Играющий (или играющие) задумывает (задумывают) день. Нужно угадать, какой день задумали. Отгадывающий предлагает выполнить следующие действия:
1) удвоить номер задуманного дня;
2) прибавить к полученному результату 5;
3) умножить новый результат на 5;
4) приписать 0 к полученному числу справа;
5) вычесть 250.
В конце отгадывающему остается только разделить на 100 полученный результат. Ответ — искомый номер дня недели.
Пусть, например, задумана пятница — шестой день. Играющий выполняет следующие действия:
1) 6 × 2 = 12;
2) 12 + 5 = 17;
3) 17 × 5 = 85;
4) 85 →850;
5) 850 – 250 = 600,
— и объявляет результат. По нему отгадывающий легко вычисляет номер задуманного дня.
Нетрудно увидеть, что “механизмы” двух рассмотренных забав очень похожи. Но если фокусы будут разнесены во времени, сходства никто не заметит…
М
атематическая забава Михаила Юрьевича Лермонтова
Рис.5. М.Ю.Лермонтов
Известно, что великий русский поэт М.Ю. Лермонтов (рис.5) был большим любителем математики и в своих вольных и невольных переездах из одного места службы в другое всегда возил с собою учебник математики. Он также любил развлекать своих знакомых математическими фокусами. Суть его “забав” сводилась к тому, что задуманное число на каком-либо этапе вычислений он предлагал вычесть, а все математические действия сводились к действиям над названными им числами. В результате — вычисления не зависели от задуманного числа, он с легкостью угадывал полученный результат.
Например:
1) к задуманному числу требовалось прибавить 150;
2) из полученного результата вычесть 36;
3) вычесть задуманное число;
4) умножить полученный результат на 5;
5) разделить на 2.
Итог вычислений можно “отгадать” — 285.
Эти действия можно описать с помощью следующих формул:
а+ 150
а+ 150 – 36 = а+ 114
а+ 114 –а= 114
114 × 5 = 570
570 : 2 = 285.
Все рассмотренные примеры убеждают нас в том, что математические фокусы не включают в себя элементы мистики, а являются результатом выполнения определенных алгоритмов.
2. Комбинаторные игры


Поиск выигрышной тактики, а, следовательно, и алгоритма несложной игры – интересная и полезная задача. Меня заинтересовали комбинаторные игры, т.е. игры, где нет элементов случайности, все правила чётко описаны, и игроки имеют полную информацию о текущей ситуации. Примерами рассматриваемых нами игр являются большинство настольных игр: шахматы, шашки, Го, крестики-нолики и многие другие (рис.6).
Рис.6. Комбинаторные игры
В математике и информатике большое распространение получили игры с камнями. Рассмотрим одну из таких игр, которая называется игрой Баше.
Играют двое. Перед ними 21 предмет, допустим, камни (также может быть 11, 16, 26 и т.д.). Игроки берут камни по очереди. За один ход можно взять 1-2-3-4 камня. Проигрывает тот, кто забирает последний камень.
Имеется выигрышная тактика для игрока, берущего камни вторым. Она заключается в том, что брать такое количество камней, которое дополняет число камней, взятых соперником на предыдущем ходе, до пяти. Этот алгоритм можно описать в виде последовательности команд:
алг Игра Баше
нач
1. Предоставить ход сопернику
2. Взять столько камней, чтобы в сумме с предыдущим ходом соперника получилось 5
3. Если остался один камень, то объявить о своём выигрыше, иначе вернуться к выполнению команды 1
кон
Игрок, строго следующий этому алгоритму, будет всегда выигрывать.
Игра Ним (камешки)
Это древняя китайская игра. В неё любили играть китайские императоры. Тем, кто у них выигрывал, отрубали голову.
Начальная позиция: куча камешков (5 штук или больше). Вместо камешков можно использовать любые мелкие предметы – пуговицы, фасоль, палочки, скрепки.
Возможные ходы: игрок забирает из кучки разрешённое число камешков.
Как определить победителя? Заключительная позиция игры: это пустая кучка камешков. При этом игрок, забравший последний камешек из кучки, выиграл. (Значит, в этой игре ничьих не бывает.)
Вот цепочка партии в Камешки (начальная позиция – 7 камешков, можно брать 1 или 2 камешка за один ход) (рис.7):
Р
ис.7
На пятом ходу партии первый забрал 2 оставшихся камешка и выиграл.
Как видно из правил, в игре Камешки неважно, какие именно камешки были в кучке до начала игры и какие именно камешки забирает игрок на своём ходу. Важно только то, сколько камешков было до начала и сколько камешков осталось после каждого хода.
Игра со спичками
В простых играх можно найти выигрышную стратегию, просто перебрав все возможные варианты ходов соперников. Для примера рассмотрим такую игру: сначала в кучке лежит 5 спичек; два игрока убирают спички по очереди, причем за 1 ход можно убрать 1 или 2 спички; выигрывает тот, кто оставит в кучке 1 спичку (рис.8).
Р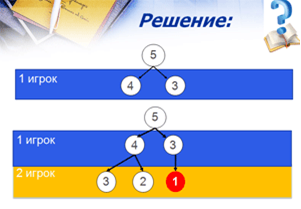
ис.8
Если осталось 3 или 2 спички, то 1-ый игрок (в обеих ситуациях) выиграет своим ходом.
Простроенная схема называется «деревом игры», она показывает все возможные варианты, начиная с некоторого начального положения (рис.9).
Р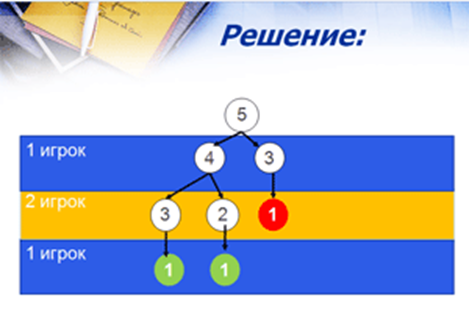
ис.9. «Дерево игры»
Проанализируем эту схему; если первый игрок своим первым ходом взял две спички, то второй сразу выигрывает; если же он взял одну спичку, то своим вторым ходом он может выиграть, независимо от хода второго игрока. Кто же выиграет при правильной игре? Для этого нужно ответить на вопросы: 1) «Может ли первый игрок выиграть, независимо от действий второго?», и 2) «Может ли второй игрок выиграть, независимо от действий первого?»
ответ на первый вопрос – «да»; действительно, убрав всего одну спичку первым ходом, 1-ый игрок всегда может выиграть на следующем ходу
ответ на второй вопрос – «нет», потому что если первый игрок сначала убрал одну спичку, второй всегда проиграет, если первый не ошибется.
Таким образом, при правильной игре выиграет первый игрок; для этого ему достаточно первым ходом убрать всего одну спичку.
3. Теория игр
Одним из создателей теории игр является Джон фон Нейман. «Есть в современной математике одна область, она носит безобидное название теории игр, но ей, несомненно, суждено сыграть очень важную роль в человековедении самого ближайшего будущего. Она занимается вопросами оптимального поведения людей при наличии противодействующего противника. Для ученого противник - это природа со всеми ее явлениями; экспериментатор борется со средой; математик - с з
агадками математического мира; инженер - с сопротивлением материалов», - Джон фон Нейман, один из основоположников кибернетики (рис.10).
Рис.10. Джон фон Нейман
Теория игр — математический метод изучения оптимальных стратегий в играх. Под игрой понимается процесс, в котором участвуют две и более стороны, ведущих борьбу за реализацию своих интересов. Каждая из сторон имеет свою цель и использует некоторую стратегию, которая может вести к выигрышу или проигрышу — в зависимости от поведения других игроков. Теория игр помогает выбрать лучшие стратегии с учётом представлений о других участниках, их ресурсах и их возможных поступках.
Под игрой в математике понимают всякое соревнование с определенной системой правил, условий и ограничений, в соответствии с которыми действуют участники игры, добиваясь выигрыша. Теория игр занимается изучением вопросов поведения и разработкой оптимальных правил (стратегий) поведения каждого из участников (игроков) в конфликтной ситуации.
Теория игр первоначально рассматривала экономические модели. Но уже с 1950-х гг. начинаются попытки применить методы теории игр не только в экономике, но в биологии, кибернетике, технике, антропологии. Во время Второй мировой войны и сразу после нее теорией игр серьёзно заинтересовались военные, которые увидели в ней мощный аппарат для исследования стратегических решений. В 1960—1970 гг. интерес к теории игр угасает, несмотря на значительные математические результаты, полученные к тому времени. С середины 1980-х гг. начинается активное практическое использование теории игр, особенно в экономике и менеджменте. За последние 20 — 30 лет значение теории игр и интерес значительно растет, некоторые направления современной экономической теории невозможно изложить без применения теории игр.
Большим вкладом в применение теории игр стала работа Томаса Шеллинга, нобелевского лауреата по экономике 2005 г. «Стратегия конфликта». Т.Шеллинг рассматривает различные «стратегии» поведения участников конфликта. Эти стратегии совпадают с тактиками управления конфликтами и принципами анализа конфликтов в конфликтологии (это психологическая дисциплина) и в управлении конфликтами в организации. В психологии и других науках используют слово «игра» в других смыслах, нежели чем в математике. Некоторые психологи и математики скептически относятся к использованию этого термина в других смыслах, сложившихся ранее. Культурологическое понятие игры было дано в работе Йохана Хёйзинга «Homo Ludens» , автор говорит об использовании игр в правосудии, культуре, этике говорит о том, что игра старше самого человека, так как животные тоже играют. Понятие игры встречается в концепции Эрика Бёрна «Игры, в которые играют люди, люди, которые играют в игры». Это сугубо психологические игры, основанные на трансакционном анализе. Понятие игры у Й.Хёзинга отличается от интерпретации игры в теории конфликтов и математической теории игр. Игры также используются для обучения в бизнес-кейсах, семинарах Г. П. Щедровицкого, основоположника организационно-деятельностного подхода. Во время Перестройки в СССР Г. П. Щедровицкий провел множество игр с советскими управленцами. По психологическому накалу ОДИ (организационно-деятельностные игры) были так сильны, что служили мощным катализатором изменений в СССР. Сейчас в России сложилось целое движение ОДИ. Критики отмечают искусственную уникальность ОДИ. Основой ОДИ стал Московский методологический кружок (ММК).
4. Применение теории игр к решению жизненных задач,
выигрышные стратегии
Обучаясь в школе, я тоже сталкиваюсь с теорией игр. Одно из заданий ЕГЭ по информатике связано с теорией игр. Оно решается с помощью построения дерева игры.
Задача: Два игрока играют в следующую игру. Перед ними лежат две кучки камней, в первой из которых 3, а во второй – 2 камня. У каждого игрока неограниченно много камней. Игроки ходят по очереди. Ход состоит в том, что игрок или увеличивает в 3 раза число камней в какой-то куче, или добавляет 1 камень в какую-то кучу. Выигрывает игрок, после хода которого общее число камней в двух кучах становится не менее 16 камней (рис.11). Кто выигрывает при безошибочной игре – игрок, делающий первый ход, или игрок, делающий второй ход? Каким должен быть первый ход выигрывающего игрока?

Рис.11
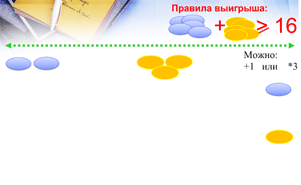
Рис.12. Правило выигрыша
Выполним заготовку дерева игры:
|
| 1 игрок | 2 игрок | 1 игрок | 2 игрок |
| (3,2) 5 | (4,2) 6 | (5,2) 7 | (15,2) 17 |
|
| (4,3) 7 | (4,4) 8 | (12,4) 16 |
| (5,3) 8 | (15,3) 18 |
| (4,9) 13 | (12,9) 21 |
| (12,3) 15 | (12,4) 16 |
| (12,2) 14 | (36,2) 38 |
|
| (4,6) 10 | (12,6) 18 |
|
| (3,3) 6 | (3,9)12 | (3,27) 30 |
|
| (3,4) 7 | (4,4) 8 | (12,4) 16 |
| (3,5) 8 | (15,3) 18 |
| (9,4) 13 | (12,9) 21 |
| (3,12) 15 | (12,4) 16 |
| (9,2) 11 | (27,2) 29 |
|
|
| (3,6)9 | (3,18) 21 |
|
|
Рис.13. «Дерево игры»
Получаем, что при правильной стратегии всегда выигрывает второй игрок. Для этого своим первым ходом ему нужно получить одну из ситуаций: (4,3), (27,2) или (18,3) – здесь числа в скобках обозначают количество камней в первой и второй кучке соответственно. В последних двух случаях он выигрывает сразу, в первом – через 1 ход.
Несомненно, что игровые задачи являются одним из самых мощных инструментов развития человеческого интеллекта. Человеку в течение всей жизни приходится не один раз оказываться в затруднительном положении, выход их которого можно найти с помощью логических рассуждений. А способность логически мыслить, и отрабатывается на решении нестандартных занимательных задач, при решении которых развивается интеллект человека. Эти задачи проверяют не знания, а умение логически рассуждать, ориентироваться в необычных ситуациях, предвидеть и действовать.
Математическая теория игр сейчас бурно развивается, рассматриваются динамические игры. Однако математический аппарат теории игр затратен. Его применяют для оправданных задач: политика, экономика монополий и распределения рыночной власти и т. п. Ряд известных ученых стали Нобелевскими лауреатами по экономике за вклад в развитие теории игр, которая описывает социально-экономические процессы. Дж. Нэш, благодаря своим исследованиям в теории игр, стал одним из ведущих специалистов в области ведения «холодной войны», что подтверждает масштабность задач, которыми занимается теория игр.
Нобелевскими лауреатами по экономике за достижения в области теории игр и экономической теории стали: Роберт Ауманн, Райнхард Зелтен, Джон Нэш, Джон Харсаньи, Уильям Викри, Джеймс Миррлис, Томас Шеллинг, Джордж Акерлоф, Майкл Спенс, Джозеф Стиглиц, Леонид Гурвиц, Эрик Мэскин, Роджер Майерсон, Ллойд Шепли, Элвин Рот.
Заключение
При работе над темой исследования я «разгадала» секреты математических фокусов, познакомилась со многими комбинаторными играми, с выигрышными стратегиями; узнала, что такое теория игр и каковы её основные элементы. А также пришла к выводу, что комбинаторные игры помогают при подготовке к ЕГЭ, а также в целом развивают логическое мышление, развивают умение предполагать возможные результаты, что так необходимо в жизни.
Я убеждена в том, что теория игр проникает во все сферы нашей жизни и может помочь в решении любых жизненных задач. Данная теория решений носит исключительно математический характер, формулирует правила, математическую логику, закономерности принятия наиболее оптимального решения, а не пытается объяснить, каким образом люди реально принимают те или иные решения. Мне было полезно познакомиться с постулатами этой теории. Я рада, что могу применить полученные знания на практике.
Что наша жизнь? Игра! Эти известные слова стали расхожими, и никому не приходит в голову относиться к ним буквально. Никому, кроме специалистов по теории игр. Они уверены, что игры - это серьезно. Кому то принимать решения трудно, кому то легко. Насколько ответственно принимаются решения, насколько они правильны? – это большой вопрос. Но решения принимаются, и будут приниматься. А какую сторону занять? Выбор за нами.
Используемые источники
Агаханов Н.Х.,Подлипский О.К. «Математика. Всероссийские олимпиады», 2015
Генкин С.А.,Интенберг И.В.,Фомин Д.В. «Математический кружок»,1994
Депман И. Рассказы о математике. Л.: Детгиз, 1954.
Севрюков П.Ф. «Подготовка к решению олимпиадных задач по математике», 2016
Шеня А.П.. Игры и стратегии с точки зрения математики. М. Изд-во МЦНМО, 2007 год
Демонстрационный вариант контрольных измерительных материалов единого государственного экзамена 2019 года по информатике и ИКТ.
Журнал «Информатика», №2, 2012 г.
Интернет – ресурсы:
http://ru.wikipedia.org/wiki/%D2%E5%EE%F0%E8%FF_%E8%E3%F0
http://www.openchess.ru/pravilaChess.php
http://inn-svistun.narod.ru/p5aa1.html









 ервая забава
ервая забава а+ 5
а+ 5