Открытый урок по алгебре в 9 класс
Тип урока: урок практикум
Тема урока «Решение систем уравнений второй степени» (Слайд 1)
Цели урока (Слайд 2):
-
Обучающие: систематизировать знания по данной теме, выработать умение решать системы уравнений, содержащие уравнения второй степени графическим способом, способами подстановки и сложения.
-
Развивающие: развивать вычислительную технику, мыслительную активность, логическое мышление, интерес к предмету; способствовать формированию ключевых понятий; выполнение заданий различного уровня сложности.
-
Воспитывающие: воспитывать внимательность, аккуратность, умения четко организовывать самостоятельную и индивидуальную работу.
Оборудование: доска, мел, линейка, карточки с заданиями для индивидуальной работы, наглядность, презентация.
Ход урока
1. Организационный момент.
а) Отметить отсутствующих;
б) объявить тему урока;
в) объявить цели урока.
2. Фронтальный опрос правил и определений по теме урока. В параллели проводится индивидуальная работа с учащимися, имеющими слабую мотивацию к учебе.
Какие способы решения систем уравнений с двумя переменными знаете?
(Графический, подстановки, сложения) (Слайд 3).
Рассмотрим графический способ. (Слайд 4)
-
Как решается система графическим способом?
(Необходимо: построить графики уравнения в одной координатной плоскости; найти координаты точек пересечения графиков, которые и будут решением системы.)
-
Почему координаты точек пересечения являются решением системы уравнений?
(Координаты точек пересечения удовлетворяют каждому уравнению системы.)
-
Как записывается решение системы уравнений, если она решается графическим способом?
(Приближенным равенством для значений переменных.)
-
От чего зависит количество решений системы уравнений при графическом способе решения?
(От количества точек пересечения.)
-
Сколько точек имеют графики, если система имеет три решения? (Три точки.)
3. Работа с наглядностью. (Слайды 5, 6, 7, 8)
-
Сколько точек пересечения имеют графики.
-
Сколько решений имеет система, если графики изображены на рисунке.
-
Совместить графики уравнений с формулами, которыми они задаются.
4. Индивидуальная работа (карточки с заданиям) с использованием шаблонов координатной плоскости.
Изобразив схематически графики уравнений, укажите количество решений системы.
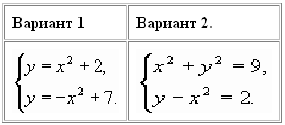
Ответ:
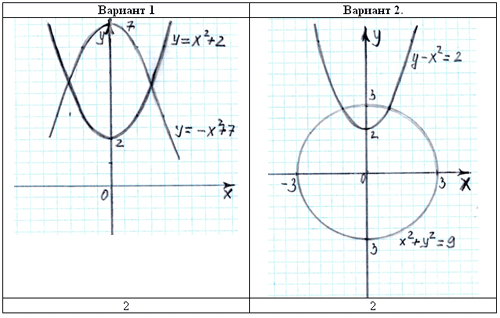
5. При графическом способе решения мы находим приближенные значения переменных. А как же найти точные значения?
(Решить систему способом подстановки или сложения.)
-
Как решить систему способом подстановки? (Слайд 9)
(Выражают из уравнения одну переменную через другую. Подставляют эту подстановку в другое уравнение. Решают полученное уравнение с одной переменной. Находят соответствующие значение второй переменной, из подстановки).
-
Есть ли разница, из какого уравнения системы получить подстановку?
(Нет. Если в систему входит уравнение 1-ой степени, то подстановку получают из этого уравнения. Если оба уравнения второй степени, то подстановку получают из любого.)
-
Как записать решение системы? (Парой чисел.)
-
Как решить систему способом сложения? (Слайд 10)
6. Устная работа. В параллели проводится индивидуальная работа с учащимися средней мотивации к учебе
а) Определите степень уравнения (Слайд 11, 12):

Ответ:
б) Выразите одну переменную через другую (слайд 13, 14):

6. Работа в тетрадях (Слайд 15): № 6.1 (а), 6.5(а), 6.11(а), 6.14(а).
7. Самостоятельная работа (карточки с заданиями) Решите систему уравнений:

Ответ:
| Вариант 1 | Вариант 2 |
| (-4;-5); (2;1) 1б | (-6;-9); (8;5) 1б |
| Решений нет 1б | (4;-1); (-4;1) 1б |
| (-0,5;-11); (8; 6) 2б | (-4;-5); (14;4) 2б |
| (-0,4;0,3); (3;2) 2б | Решений нет 2б |
| (3;1) 3б |
8. Подведение итогов. Занесите свои результаты в оценочный лист.
| Ф.И.
ученика | Индивидуальная | Устная |
Самостоятельная
| Письменная | Итоговая
оценка |
|
|
|
|
|
|
|
9. Домашнее задание (Слайд 16): п.6, с.41-43, № 6.1 (б), 6.5(б), 6.11(б), 6.14(б). доп задание (6.22)
Литература:
1.Учебник “Алгебра 9 класс”, авторы: А.Г. Мардкович, П. В. Семенов., “Мнемозина”, 2014.
2.Уроки алгебры в 9 классе, авторы О.В. Занина, И.Н.Данкова, Москва “Вако”, 2009.
3.Дидактические материалы по алгебре 9 класс, авторы В.И.Жохов и др., “Просвещение”, 2015.
4.Открытый банк задач по ГИА.
































