МОБУ Городская Классическая Гимназия
Открытый урок по математике (геометрия) 8 класс
по теме: «синус, косинус, тангенс острого угла прямоугольного треугольника»
Цель урока:
Ввести понятие синуса, косинуса и тангенса острого угла прямоугольного треугольника, ознакомить учащихся с основным тригонометрическим тождеством и показать его применение в процессе решения задач.
Этапы урока:
-
Организационный момент (2 минута).
-
Проверка домашнего задания (5 минуты)
-
Актуализация опорных знаний (5 минут).
-
Сообщение темы урока, постановка его целей (2 минуты).
-
Изучение нового материала (15 минут).
-
Решение упражнений (12 минут).
-
Подведение итогов урока (5 минут).
-
Домашнее задание (1 минута).
Ход урока:
1. Организационный момент.
(готовность к уроку, отсутствующие, учитель проверяет наличие домашнего задания, спрашивает не было ли трудностей при выполнении домашнего задания, запись числа, классной работы)
2. Проверка домашнего задания.
Учащимся задано на дом следующее задание: № 606, 607, 628, 629. Повторить свойства прямоугольного треугольника.
Учащиеся обмениваются своими тетрадями с соседями по парте и проверяют с моей помощью домашнее задание, оценивают работу соседа, ставят оценку за работу.
3. Актуализация опорных знаний
Провести общий анализ самостоятельной работы, решить задачи, с которыми не справилось большинство учащихся. Провести работу над ошибками: на интерактивной доске записаны готовые ответы и указания к задачам самостоятельной работы. Ученики находят и исправляют свои ошибки. Учитель по мере необходимости оказывает индивидуальную помощь.
4. Сообщение темы и целей урока.
Учитель сообщает тему урока, ученики записывают ее в тетрадь. Учитель сообщает цели урока.
5. Изучение нового материала.
Учитель вводит понятие катетов, прилежащих и противолежащих углу.
Вводится понятие синуса, косинуса, тангенса острого угла прямоугольного треугольника, их обозначения.
Определения:
Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему катету.
На доске и в тетрадях рисунок и запись:
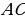 – катет, прилежащий
– катет, прилежащий 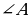 ,
,
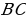 – катет, противолежащий
– катет, противолежащий 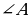 .
.
Вычисление значений синуса, косинуса и тангенса с помощью микрокалькулятора.
Вывод формулы
а) 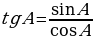 ,
,
б) 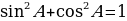 .
.
Показать, что последнее равенство называется основным тригонометрическим тождеством.
6. Решение упражнений.
Задача: доказать, что если острый угол одного прямоугольного треугольника равен острому углу другого треугольника, то синусы этих углов равны и тангенсы этих углов равны.
Наводящие вопросы:
- если острый угол одного прямоугольного треугольника равен острому углу другого треугольника, то что можно сказать про эти треугольники?
- что можно сказать про об отношениях их сходственных сторон?
- что называют основным свойством пропорции?
- что можно сказать об отношении противолежащего катета к гипотенузе?
7. Итоги урока.
Самостоятельная работа
1 ВАРИАНТ
1. В треугольнике  угол
угол 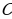 прямой,
прямой, 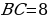 ,
, 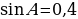 . Найдите
. Найдите 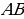 .
.
2. Катеты прямоугольного треугольника равны 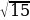 и 1. Найдите синус наименьшего угла этого треугольника.
и 1. Найдите синус наименьшего угла этого треугольника.
3. В прямоугольном треугольнике  катет
катет  , а высота
, а высота 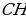 , опущенная на гипотенузу, равна
, опущенная на гипотенузу, равна 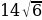 . Найдите синус
. Найдите синус 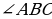 .
.
2 ВАРИАНТ
1. В треугольнике  угол
угол 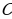 прямой,
прямой, 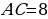 ,
, 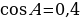 . Найдите
. Найдите 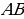 .
.
2. Катеты прямоугольного треугольника равны 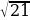 и 2. Найдите синус наименьшего угла этого треугольника.
и 2. Найдите синус наименьшего угла этого треугольника.
3. В прямоугольном треугольнике  катет
катет 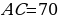 , а высота
, а высота 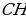 , опущенная на гипотенузу, равна
, опущенная на гипотенузу, равна 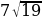 . Найдите синус
. Найдите синус 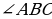 .
.
8. Домашнее задание:
1. П. 68, вопросы 15–17 (учебник, стр. 159).
2. Решить задачу № 73 (рабочая тетрадь).
3. Решить задачи № 591 (в, г), 592 (б, г, е), 593 (в, г).






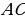 – катет, прилежащий
– катет, прилежащий 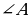 ,
,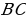 – катет, противолежащий
– катет, противолежащий 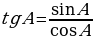 ,
,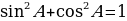 .
. угол
угол 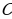 прямой,
прямой, 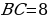 ,
, 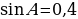 . Найдите
. Найдите 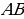 .
.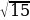 и 1. Найдите синус наименьшего угла этого треугольника.
и 1. Найдите синус наименьшего угла этого треугольника. , а высота
, а высота 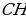 , опущенная на гипотенузу, равна
, опущенная на гипотенузу, равна 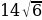 . Найдите синус
. Найдите синус 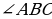 .
.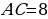 ,
, 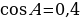 . Найдите
. Найдите 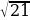 и 2. Найдите синус наименьшего угла этого треугольника.
и 2. Найдите синус наименьшего угла этого треугольника.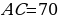 , а высота
, а высота 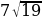 . Найдите синус
. Найдите синус 

















