Тема урока: "Решение задач на применение теоремы Пифагора"
Цель урока: формирование умений, навыков решать задачи, используя теорему Пифагора;
Цели:
Образовательные – Обобщить и систематизировать знания учащихся по теме, учить учащихся применять полученные знания к решению практических и древних задач ;
Развивающие – развивать внимание учащихся, логическое мышление, математическую речь;
Воспитательные – прививать интерес к геометрии, посредством урока воспитывать внимательное отношение друг к другу, прививать умение слушать товарищей, взаимовыручку, самостоятельность.
Тип урока: урок закрепления полученных знаний
Формы работы: фронтальная, индивидуальная, самостоятельная
Оборудование: компьютер, проектор, экран, презентация
Ход урока:
1. Мотивационно-организационный этап.
Мы продолжаем изучение одной из самых известных теорем древности, теорему Пифагора. Значение теоремы Пифагора состоит и в том, что с ее помощью можно доказать многие другие теоремы и решить множество задач. Где нам пригодится теорема Пифагора? Сегодня мы с вами рассмотрим некоторые задачи.
2. Актуализация опорных знаний.
Еще в 17 веке немецкий астроном и математик И. Кеплер сказал, что геометрия обладает двумя великими сокровищами. Первое – это теорема Пифагора, которую можно сравнить с мерой золота…
Напомните, пожалуйста, формулировку теоремы Пифагора. (ответы учащихся)
А обратная теорема? (ответы учащихся)
Для того чтобы наша работа была успешной, давайте повторим некоторые геометрические факты.
Дайте, пожалуйста, определение прямоугольного треугольника?
Как называются стороны прямоугольного треугольника?
Один из углов прямоугольного треугольника равен 25°. Чему равны остальные углы?
- Один из углов прямоугольного треугольника равен 30°, катет, противолежащий ему, равен 11 см. Чему равна гипотенуза?
- Катет прямоугольного треугольника равен 8 дм, гипотенуза – 16 дм. Найдите углы треугольника
3. Проверочная работа (тест )
Вот сейчас с помощью тестов мы и проверим, насколько уверенно вы ориентируетесь в теореме Пифагора. Тесты несложные, но их результаты будут учтены при выставлении оценки за урок. У вас 1 минута
Тест (вариант 1)
1. К каким треугольникам можно применить теорему Пифагора?
а) любым; б) прямоугольным; в) равносторонним
2. Верно ли, что в прямоугольном треугольнике любой из катетов меньше гипотенузы?
а) нет; б) не знаю; в) да
3. Гипотенуза прямоугольного треугольника равна 5 см, катет 3 см. Найти длину второго катета?
а) 8 см; б) 4 см; в) 10 см
4. Теорема Пифагора записывается так:
а) а2 = с2 - в2 б) в2 = с2 – а2 в) с2 = а2+ в2
5. В прямоугольном треугольнике углы равны:
а) 90; 60; 90; б) 45; 90;45; в)60; 30; 60
Тест (вариант 2)
1. К каким треугольникам можно применить теорему Пифагора?
а) любым; б) прямоугольным; в) равносторонним
2. Верно ли, что в прямоугольном треугольнике гипотенуза больше любого из катетов?
а) нет; б) не знаю; в) да
3 Чему равна гипотенуза прямоугольного треугольника с катетами 9 см и 12 см?
а) 8 см; б) 15 см; в) 10 см
4. В прямоугольном треугольнике углы равны:
а) 90; 30; 90; б) 45; 125;45; в)90; 30; 60
5.Египетский треугольник имеет стороны:
а) 3,4,5 б) 3,5,7 в) 10,13,14
Ответы: В-1
1.б 2.в 3.б 4.в 5. б
В-2
1.б 2.в 3.б 4.в 5. а
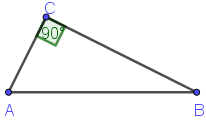
4. Решение задач устно: Задача 1
В треугольнике ABC: ∠C=90∘, AB=8 и BC=5. Найдите квадрат AC (AC2 = ?).
Задача 2
Может ли прямоугольный треугольник иметь стороны: 3, 4, 5?
Задача 3
Дано прямоугольный треугольник ABC. ∠C=90∘, и AC=3, BC=4. Найдите длину AB.

Задача 4
Есть прямоугольный треугольник ABC, ∠C=90∘, и AC=7, AB=25. Найдите длину BC.

Начало формы
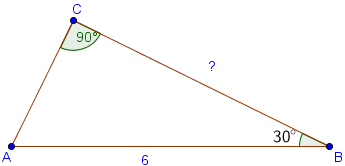
Задача 5 Угол С=90, а угол B=30. Гипотенуза АВ = 6. Найдите сторону BC.
5. Пифагор организовал свой пифагорейский орден и школу философов и математиков. Туда принимали с большими церемониями и после долгих испытаний. Здесь существовал декрет, по которому авторство всех математических работ приписывалось самому Пифагору. В школе была очень серьезная дисциплина. Пифагор и его ученики были трудолюбивы. Вот их заповеди.
Задания ( работа в парах )
Карточка для B – I.
| №1. Катеты прямоугольного треугольника равны 3 и 4 см. Вычислите его гипотенузу. | №2. Диагональ прямоугольника ABCD - 10 см. Сторона АВ = 8 см. Вычислите сторону ВС. |
|
Ответы к задаче №1
|
Ответы к задаче №2
|
|
5 – не гоняйся за счастьем
|
4 – оно присутствует около тебя
|
| 6 – не бегай за счастьем | 6 – оно всегда находится в тебе самом |
Ответ: Не гоняйся за счастьем, оно всегда находится в тебе самом.
Карточка для B – II.
| №1. Вычислите катет прямоугольного треугольника, если другой катет равен 8, а гипотенуза 10 см. | №2. Стороны прямоугольника равны 12 см и 5 см. Вычислите длину диагонали. |
|
Ответы к задаче №1
|
Ответы к задаче №2
|
| 4 – формулы | 13 – управляют миром |
|
6 – числа
|
14 – правят всем
|
Ответ: Числа управляют миром.
Карточки для B – III
| №1.Вычислите катет прямоугольного треугольника, если две другие его стороны равны 15 и 17 см. | №2. Найти боковую сторону равнобедренного треугольника, если основание равно 8см, а высота, опущенная на основание - 3см. |
|
Ответы к задаче №1
|
Ответы к задаче №2
|
| 8 – либо молчи | 5 – либо говори то, что ценнее молчания |
| 64 – хочешь-молчи | 6 – или говори о том, что интересно всем |
Ответ: Либо молчи, либо говори то, что ценнее молчания.
Проверка результатов (чтение афоризмов) (каждая группа предлагает свои ответы):
1.Ответ: Не гоняйся за счастьем, оно всегда находится в тебе самом.
2.Ответ: Числа управляют миром.
3.Ответ: Либо молчи, либо говори то, что ценнее молчания.
6. Задачи на готовых чертежах. ( Решение задач)
7. Дом. задание: подготовиться к контрольной работе, № 487
8. Рефлексия.
У каждого ученика лежит таблица, которую они заполняют в процессе урока. В конце урока сдают таблицу учителю.
| Фамилия, имя |
| 1 | Вспомни! (теория- тест) |
|
|
|
|
|
|
| 2 | Заповеди Пифагора |
|
|
|
|
|
|
| 3 | Решение задач |
|
|
|
|
|
|
| Итого |
|
Рефлексия проводится в процессе заполнения следующей таблицы.
| Фамилия, имя |
| Я умею решать задачи |
|
| Я умею применять теорему Пифагора |
|
| Мне важно научиться выполнять эти задания |
|
| Мне было интересно на уроке |
|
| Мне было неинтересно на уроке |
|
| Мне это не нужно |
|
| Моя оценка урока (от 1 до 5) |
|
высказывание Д. Пойя «Где есть желание, найдется путь».
Я хотела бы завершить наш урок словами знаменитого математика Джорджа Пойя.
Благодаря нашему стремлению к новым знаниям, мы смогли сегодня проделать
путь, который позволил понять, как важна и нужна и в наше время теорема Пифагора.
Приложение 1.
| Фамилия, имя |
| 1 | Тест |
|
|
|
|
|
|
| 2 | Заповеди Пифагора |
|
|
|
|
|
|
| 3 | Решение задач |
|
|
|
|
|
|
| Итого |
|
Тест (вариант 1)
1. К каким треугольникам можно применить теорему Пифагора?
а) любым; б) прямоугольным; в) равносторонним
2. Верно ли, что в прямоугольном треугольнике любой из катетов меньше гипотенузы?
а) нет; б) не знаю; в) да
3. Гипотенуза прямоугольного треугольника равна 5 см, катет 3 см. Найти длину второго катета?
а) 8 см; б) 4 см; в) 10 см
4. Теорема Пифагора записывается так:
а) а2 = с2 - в2 б) в2 = с2 – а2 в) с2 = а2+ в2
5. В прямоугольном треугольнике углы равны:
а) 90; 60; 90; б) 45; 90;45; в)60; 30; 60
Рефлексия проводится в процессе заполнения следующей таблицы.
| Фамилия, имя |
| Я умею решать задачи |
|
| Я умею применять теорему Пифагора |
|
| Мне важно научиться выполнять эти задания |
|
| Мне было интересно на уроке |
|
| Мне было неинтересно на уроке |
|
| Мне это не нужно |
|
| Моя оценка урока (от 1 до 5) |
|
| Фамилия, имя |
| 1 | Тест |
|
|
|
|
|
|
| 2 | Заповеди Пифагора |
|
|
|
|
|
|
| 3 | Решение задач |
|
|
|
|
|
|
| Итого |
|
Тест (вариант 2)
1. К каким треугольникам можно применить теорему Пифагора?
а) любым; б) прямоугольным; в) равносторонним
2. Верно ли, что в прямоугольном треугольнике гипотенуза больше любого из катетов?
а) нет; б) не знаю; в) да
3 Чему равна гипотенуза прямоугольного треугольника с катетами 9 см и 12 см?
а) 8 см; б) 15 см; в) 10 см
4. В прямоугольном треугольнике углы равны:
а) 90; 30; 90; б) 45; 125;45; в)90; 30; 60
5.Египетский треугольник имеет стороны:
а) 3,4,5 б) 3,5,7 в) 10,13,14
Рефлексия проводится в процессе заполнения следующей таблицы.
| Фамилия, имя |
| Я умею решать задачи |
|
| Я умею применять теорему Пифагора |
|
| Мне важно научиться выполнять эти задания |
|
| Мне было интересно на уроке |
|
| Мне было неинтересно на уроке |
|
| Мне это не нужно |
|
| Моя оценка урока (от 1 до 5) |
|

















