Открытый урок по геометрии по теме: Сину,косину,тангенс и котангенс острого угла прямоугольного треугольника

Актуализация

опорных

знаний

Актуализация опорных знаний

Какой треугольник называется прямоугольным ?

A

B

C

Как называются стороны

прямоугольного треугольника ?

B

A

C

ВС - гипотенуза

АВ и АС - катеты

С – острые углы

В и

Какие свойства, связанные с углами и сторонами прямоугольного треугольника, вы знаете?

B

если

то

A

C

, тогда

A

B

C

Если

будет равнобедренным

и

Цели урока.

Образовательные:

формировать понятия синуса, косинуса и тангенса острого угла прямоугольного треугольника;

Развивающие:

развивать способности к самостоятельному планированию и организации работы; навыки коррекции собственной деятельности через применение информационных технологий; умение обобщать, абстрагировать и конкретизировать знания

Воспитательные:

воспитывать познавательный интерес к математике, информационную культуру и культуру общения, самостоятельность, способность к коллективной работе.

Актуализация опорных знаний,

необходимых для творческого применения знаний

Математический диктант

1.Закончи предложение: «Треугольник, у которого один угол прямой

называется…»

А) остроугольный

Б) равнобедренный

В) равносторонний

Г) прямоугольный

2. Отметь прямоугольный треугольник:

3. Как называются стороны в прямоугольном треугольнике?

А) боковые стороны

Б) основания

В) катеты и гипотенуза

Г) параллельные стороны

4. Один из острых углов прямоугольного треугольника равен 30 °, чему равен другой острый угол?

А) 90°

Б) 60°

В) 30°

С) 180°

5. Выберите формулу площади

прямоугольного треугольника:

А) S = a ·b

Б) S = a·h

B) S = a·b·sin α

Г) S = ٕ√ p(p-a)(p-b)(p-c)

6. Катет прямоугольного треугольника, лежащий напротив угла в 30 °, равен 15см. Чему равна гипотенуза?

А) 15см

Б) 7,5см

В) 20см

Г) 30см

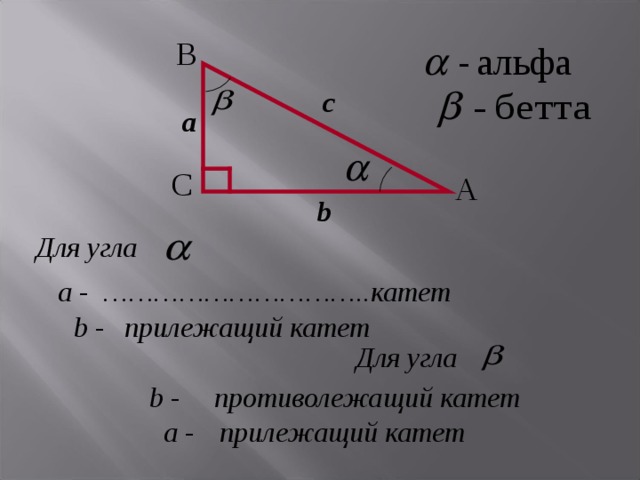
B

с

а

C

A

b

Для угла

a -

………………………… ..катет

прилежащий катет

b -

Для угла

противолежащий катет

b -

a -

прилежащий катет

Синусом острого угла в прямоугольном треугольнике называется отношение ………….. катета к гипотенузе

В

BC

A



sin

AB

А

С

Косинусом острого угла в прямоугольном треугольнике называется отношение прилежащего катета к …………….

В

AC

cos

A



AB

А

С

Тангенсом острого угла в прямоугольном треугольнике называется отношение …………….. катета к прилежащему

В

BC

tg

A



AC

А

С

Котангенсом острого угла в прямоугольном треугольнике называется отношение ………….. катета к противолежащему

В

AC

сtg

A



BC

А

С

Основное тригонометрическое тождество

Оценивание выполнения математического диктанта

Эти правила позволяют , зная одну из сторон прямоугольного треугольника и острый угол , находить две другие стороны; зная две стороны, находить острые углы

c

а

b

a = c sin a = b tg

b = c cos b = a ctg

Основные тригонометрические формулы

Основное тригонометрическое тождество

Основное тригонометрическое тождество

Используя формулы синуса и косинуса получаем

по теореме Пифагора

отсюда следует

sin 2 A + cos 2 A = 1

Значения синуса, косинуса и тангенса для углов 30 0 , 45 0 , 60 0

Значения синуса, косинуса и тангенса для углов 30 0 , 45 0 , 60 0 .

30 0

sin

45 0

cos

60 0

tg

1

Найти: 1) sin  A,

4) сtg  A,

2) cоs  A,

3) tg  A,

Ответ:

sin  A=

Ответ:

соs  A=

В

tg  A=

сtg  A=

13 см

5см

С

А

Самостоятельная работа

Задания на готовых чертежах

Оценивание опорных знаний

Задание на дом:

п. 66, в. 15-17, № 591(в, г), 593(б, г), 592 * (а, б) .

Творческий проект по геометрии

8 класс

Проект

по геометрии

8 класс

на тему

ДВА БРАТА

СИНУС

И КОСИНУС

Основополагающий вопрос

Какие загадки таят в себе синус и косинус?

2 группы учащихся

историки

изучают историю появления синуса и косинуса и их определения и свойства

практики

изучают построение графиков, тригонометрические формулы с синусом и косинусом

До встречи

на защите!

Лист выполнения работы по проекту

«Два брата – синус и косинус»

Учащиеся в ходе выполнения работы заполняют эту таблицу

ФИО

Название проекта

Название группы

Состав группы

Цели и задачи поставленные перед работой

Результат

Список литературы

Критерии оценки презентации

По каждому пункту учитель и группа выставляют оценку, потом берется средняя оценка

№

Критерии

1.

Наличие проблемного вопроса

2.

Оценка группы

Оценка учителя

Цели и задачи

3.

4.

Содержание работы

Список использованных материалов

5.

Презентация оформлена для лучшего восприятия передаваемого материала

6.

Средняя оценка

Информационные материалы.

• Пифагор. Занимательная математика. Халамайзер А.Я. Москва
• «Высшая школа» 1994г.
• Живая математика. Перельман Я. И. Москва «Наука» 1978 г.
• Интеллектуальный пир. Серия «Клуб эрудитов» Выпуск 2. Кострома ИМЦ «Вариант» 1993 г.
• Коллекция 80000 анимаций. - www . animashky . ru
• Большая энциклопедия Кирилла и Мефодия, 8 CD-ROM, 2002 г.
• Электронные ресурсы сайта «Сеть творческих учителей»
• Электронные ресурсы сайта «Фестиваль педагогических идей «Открытый урок»
• Учебное электронное пособие «Математика 5-11», Дрофа
• Учебно-методическое пособие. Взаимосвязь теории с практикой в процессе изучения математики. Возняк Г.М., Маланюк М.П. Киев. «Радянська школа»