Открытый урок по математике на тему: "Объёмы тел вращения"

Открытый урок в 11 классе на тему:

«Объемы тел вращения»

Цели урока:

• Обучающая:

  • систематизировать и обобщить знания учащихся по теме «Объемы».

• Развивающая:

  • формирование умений применять приемы: сравнения, обобщения, выделения главного, анализировать условие задачи, составлять модель решения;

  • развитие умений и навыков применять математические знания к решению практических задач, ориентироваться в простейших геометрических конструкциях.

• Воспитательная:

  • формирование информационной культуры, активности, мобильности, коммуникативности.

Задачи урока:

• Выявление уровня подготовки учащихся по геометрии по данной теме, систематизирование полученных знаний с помощью приема «Кластер»;

• Развитие и реализация творческих способностей личности;

• Применение различных приемов организации интеллектуального труда;

• Применение навыков анализа, синтеза, выделения главного.

Технологии, применяемые на уроке:

• Информационно-коммуникативные (цивилизованное и осознанное выполнение поиска, отбора, преобразования, передачи, представления, хранения любых видов информации);

• Проблемный диалог (на уроке дети участвуют в формулировке темы и целей урока; вырабатывают вместе с учителем алгоритмы выполнения заданий; учатся оценивать и корректировать свою деятельность);

• Прием «Кластер» (разноуровневый подход к выполнению учащимися одинакового задания);

• Оценивание учебных успехов (ученик самостоятельно оценивает результат своих действий, избавляется от страха перед школьным контролем, создается комфортная обстановка, сберегается его психологическое здоровье).

План урока:

I. Организационный момент

II. Устная работа

III. Тест

IV. Обобщение и коррекция  опорных знаний по теме «Объемы многогранников и тел вращения»

V. Работа в группах

VI. Решение задач, соответствующих уровню задач №14 из сборника заданий ЕГЭ

VII. Подведение итогов урока

Ход урока

I. Организационный момент

II. Устная работа

1) Проверка знаний учащихся по теме «Тригонометрические соотношения в прямоугольном треугольнике». (слайд)

2) Решение задач на готовых чертежах. (слайды)

Задача 1

Задача 2

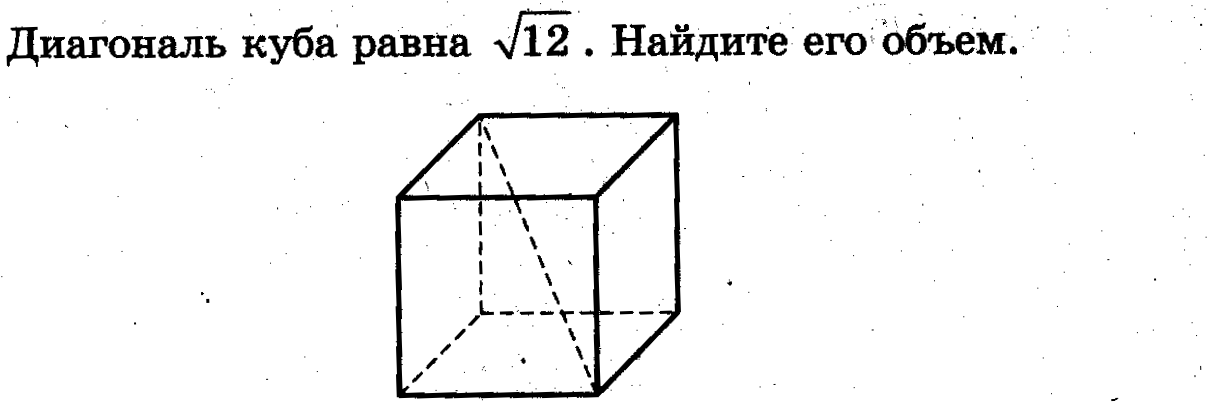
Задача 3

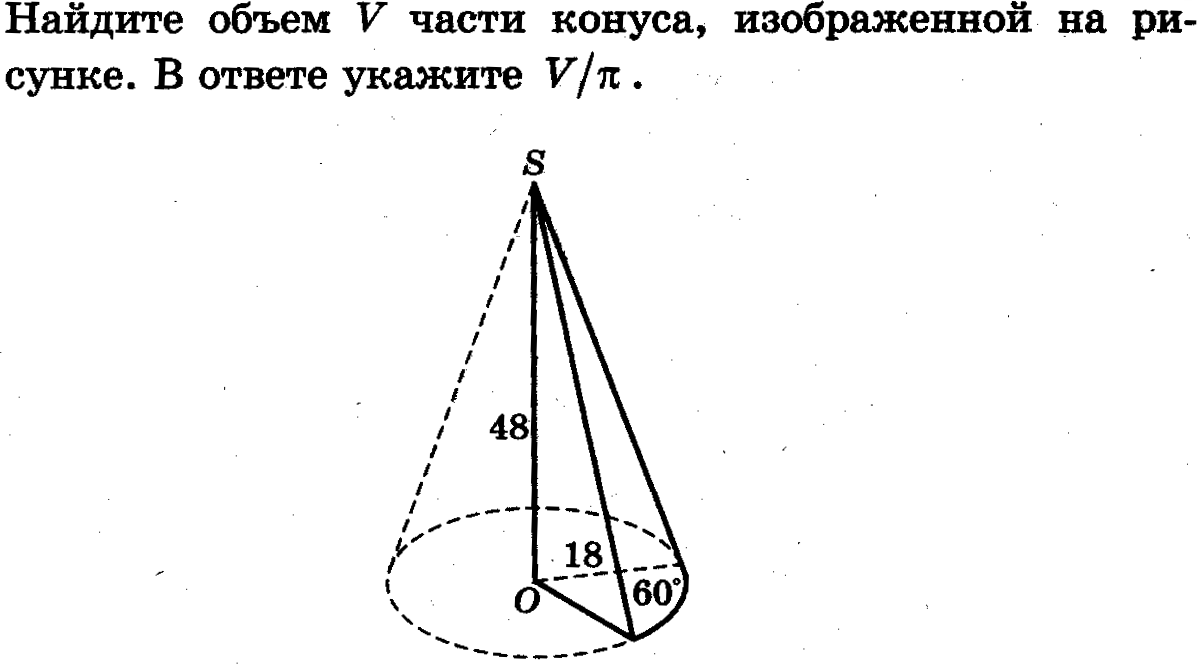
Задача 4

Задача 5

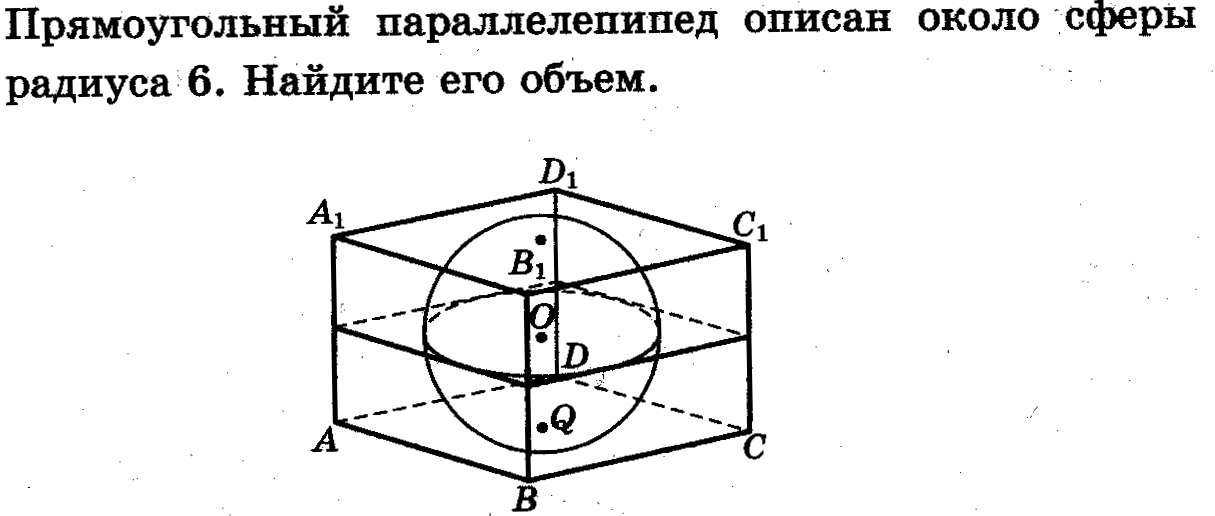
Задача 6

3) Какие формулы вы использовали для решения этих задач?

III. Тест (задачи на нахождение объемов тел из открытого банка ЕГЭ) с последующей самопроверкой

IV. Обобщение и коррекция  опорных знаний по теме «Объемы многогранников и тел вращения»

Учащимся предлагается кластер по теме «Объемы».

Необходимо записать виды многогранников и тел вращения, формулы для вычисления объемов данных фигур.

Предполагается разноуровневая индивидуальная работа учащихся с последующей самопроверкой. (слайд)

Рефлексия.

V. Работа в группах

Первая группа

Задача. Круговой сектор с углом 30⁰ и радиусом R вращается около одного из боковых радиусов. Найдите объем полученного тела вращения.

Решение

При вращении получается сектор с углом 60⁰ и радиусом R.

Посмотрим осевое сечение тела вращения. Очевидно, что высота шарового сегмента равна .

Из треугольника ВОС: ОС=ОВ, тогда    . Объем шарового сектора равен:  .

Ответ:  .

Вторая группа

Задача. При взрыве заряда взрывчатого вещества воронка действия имеет вид конуса, где   - линия наименьшего сопротивления, а r-радиус воронки. Определить объем взорванной породы в пределах конуса разрыхления, если  = =1,5м.

Решение

Объем конуса разрыхления найдем по формуле V= , то V= . Зная, что  =1,5м, имеем V=  (м³).

Ответ: объем взорванной породы 3, 54 м³.

Третья группа.

Задача. Сколько железнодорожных платформ грузоподъемностью 25 т каждая нужно для перевозки кучи угля, имеющего форму конуса с высотой Н=7,5 м, если плотность угля  =1300 кг/см³, а уголь естественного откоса  =50⁰?

Решение

Объем кучи угля . Так как   , то  , а масса кучи угля составляет: . Число железнодорожных платформ определяем по формуле  ; (пл.).

Ответ: для перевозки угля нужно 16 платформ.

Четвертая группа

Задача: Требуется установить резервуар для воды емкостью 10 м³ на площади размером 2,5х 1,75 м, служащей для него. Найдите высоту резервуара.

Решение

Резервуар имеет форму прямоугольного параллелепипеда. Его объем равен:  . Отсюда  (м)

Ответ: высота резервуара равна 2, 29 метров.

Пятая группа

Задача: Кирпич размером 25х12х6,5 см имеет массу 3,51 кг. Найдите его плотность.

Решение

Кирпич имеет форму прямоугольного параллелепипеда. Плотность равна  . Найдем  . Найдем 

Ответ: плотность кирпича  .

Шестая группа

Задача. Чугунная труба имеет квадратное сечение, ее внешняя (сторона) ширина

25 см, толщина стенок 3 см. Какова масса одного погонного метра трубы (плотность чугуна  )?

Решение

1. Найдем внутреннюю ширину трубы 

2.  , где  - объем металла, из которого сделана труба. Следовательно,  .

Найдем  . Он равен разности объемов  ₁ и  ₂ погонного метра трубы:

 или  ₁=25 = .

Найдем  .

Ответ: масса одного погонного метра чугунной трубы равна 193 кг.

После выполнения группами заданий проводится взаимопроверка. Группы меняются заданиями с решениями попарно:

Учащиеся групп обсуждают решение, исправляют ошибки и выставляют оценки за теоретические вопросы. Потом работы с выставленными оценками возвращаются в группы для обсуждения вклада каждого в решение проблемы.

VI. Решение задач, соответствующих уровню задач №14 из сборника заданий ЕГЭ

Задача 1

Решение:

Ответ: .

Задача 2

Решение:

Объем пирамиды равен .

(по 2 углам), следовательно , следовательно .

Из прямоугольного треугольника SGH: ; .

Сторона квадрата АВ=2GH, АВ=;

Площадь основания пирамиды равна ; , значит

Объем пирамиды равен .

Ответ: .

Задача 3

При выполнении домашнего задания к уроку использован дифференцированный подход к учащимся. Двум учащимся это задание было предложено для самостоятельного решения.

В правильный октаэдр вписана сфера. Определите объем сферы, если площадь поверхности октаэдра равна .

Решение:

;

;

.

Ответ: .

VII. Подведение итогов урока

1) Домашнее задание: Сборник под ред. Ященко и др. Вариант 16. Задачи №4, №6, №9, №14.

Комментарий к домашнему заданию: Информацию для решения домашнего задания вы найдете в материалах сегодняшнего урока.

2) Выставление оценок.